FT细化校正阶次全息谱分析方法

汪华平，汤宝平，韩 延，秦 毅

(重庆大学 机械传动国家重点实验室，重庆 400030)

针对旋转机械故障监测进行多通道多信息融合方法主要有三种：全谱理论(Full-Spectrum)[1]、全矢谱理论(Vector-Spectrum)[2]及全息谱(Holo-Spectrum)[3]。而全息谱通过对相互垂直两方向振动信号各倍频幅值、相位信息融合以椭圆形式直观表达转子的运动轨迹，能较好对转子横向裂纹、不平衡、弯曲、动静部件径向摩擦、油膜涡动、轴承座松动等故障进行识别[4]。

转速稳定情况，对互相垂直的两方向振动信号进行FFT分析可得转速频率的倍频分量幅值及相位信息。但在极端环境及特殊工况下，旋转机械转速极不稳定，所得振动信号非平稳，如风电机组在正常运行时转速不稳定，不能通过FFT分析直接提取各倍频分量。为解决变转速下全息谱分析问题，魏玉果等[5-6]将阶次跟踪引入全息谱分析，通过阶次重采样获得各阶次分量幅值及相位信息，再进行全息谱分析，称阶次全息谱。与传统全息谱分析因各倍频幅值、相位存在误差需校正相同，阶次全息谱分析在阶次谱计算中也存在误差，同样需校正。转速不稳定时由于进行阶次重采样，阶次分量会很明确，阶次全息谱只需计算部分阶次；传统的全息谱校正方法[7-9]不适合阶次全息谱校正，而FT细化校正法适合对局部进行细化校正，且在密集阶次谱情况下也能获得较高精度，较适合阶次全息谱校正，由此提出FT细化校正阶次全息谱分析方法。

1 基于三次样条插值的阶次全息谱

1.1 基于三次样条插值的阶次全息谱分析方法

阶次跟踪技术通过振动信号、转速信号结合实现振动信号等角度采样。对阶次跟踪技术的研究主要分两大类：①硬件式阶次跟踪[10],直接通过模拟设备实现对振动信号等角度采样；②计算式阶次跟踪(Computed Order Tracking COT)。硬件式阶次跟踪设备较昂贵且安装不便，故本文采用计算阶次跟踪技术中较精确的三次样条插值计算阶次跟踪[11]。即用三次样条插值获得等角度采样点序列号，再据采集的X，Y方向振动信号序列用插值滤波重采样完成阶次跟踪，具体步骤如下：

(1) 用同一采样频率fs同时采样获得互相垂直的振动信号序列X(n)，Y(n)及转速脉冲信号序列S(n)。

(2) 对转速脉冲信号进行三次样条插值，据所选角域采样频率Os(即等角度采样时每转采样点数)及每转所采脉冲数求出所需等角度重采样序列号T(n)。

(3) 据所得等角度重采样序列号T(n)，用插值滤波器对原始采样数据插值以获得信号等角度采样X(T(i))，Y(T(i))：

(1)

(2)

(3)

式中：i= 0,1,2,3…n为重采样后序列号i，k的取值在T(i)附近点；hs(t)为内插函数。由此获得X，Y方向角域平稳信号。

(4) 求出X，Y两方向阶次谱，获得各阶次幅值及相位fx，Ax，ax，fy，Ay，ay。将两方向振动信号各阶次写成以t为参数的方程为

X=Axsin(fxt+ax)

(4)

Y=Aysin(fyt+ay)

(5)

(5) 消去式(4)、(5)参数t，可得各倍频全息谱方程为

(6)

进而可计算出全息谱中重要参数，如长短轴、离心率、正余弦系数等。

1.2 基于三次样条插值的阶次全息谱仿真分析

用一组在二倍频含密集频谱的非平稳模拟信号X(t)，Y(t)进行阶次全息谱分析，表达式为

X(t)=sin(2πω+π/6)+0.7sin(4πω+0.25π)+

0.1sin(4.03πω+0.25π)+0.5sin(6πω+0.33π)+

0.3sin(8πω+0.5π)

(7)

Y(t)=sin(2πw+0.17π)+0.7sin(4πw+0.33π)+

0.1sin(4.03πw+0.33π)+0.6sin(6πw+0.83π)+

0.3sin(8πw+π)

(8)

方便模拟，取w=at2/2，旋转机械工频即转速频率为at，本文用加速度a=100 r/s2模拟旋转机械转速变化。取采样频率1 024 Hz、采集1 024点见图1。

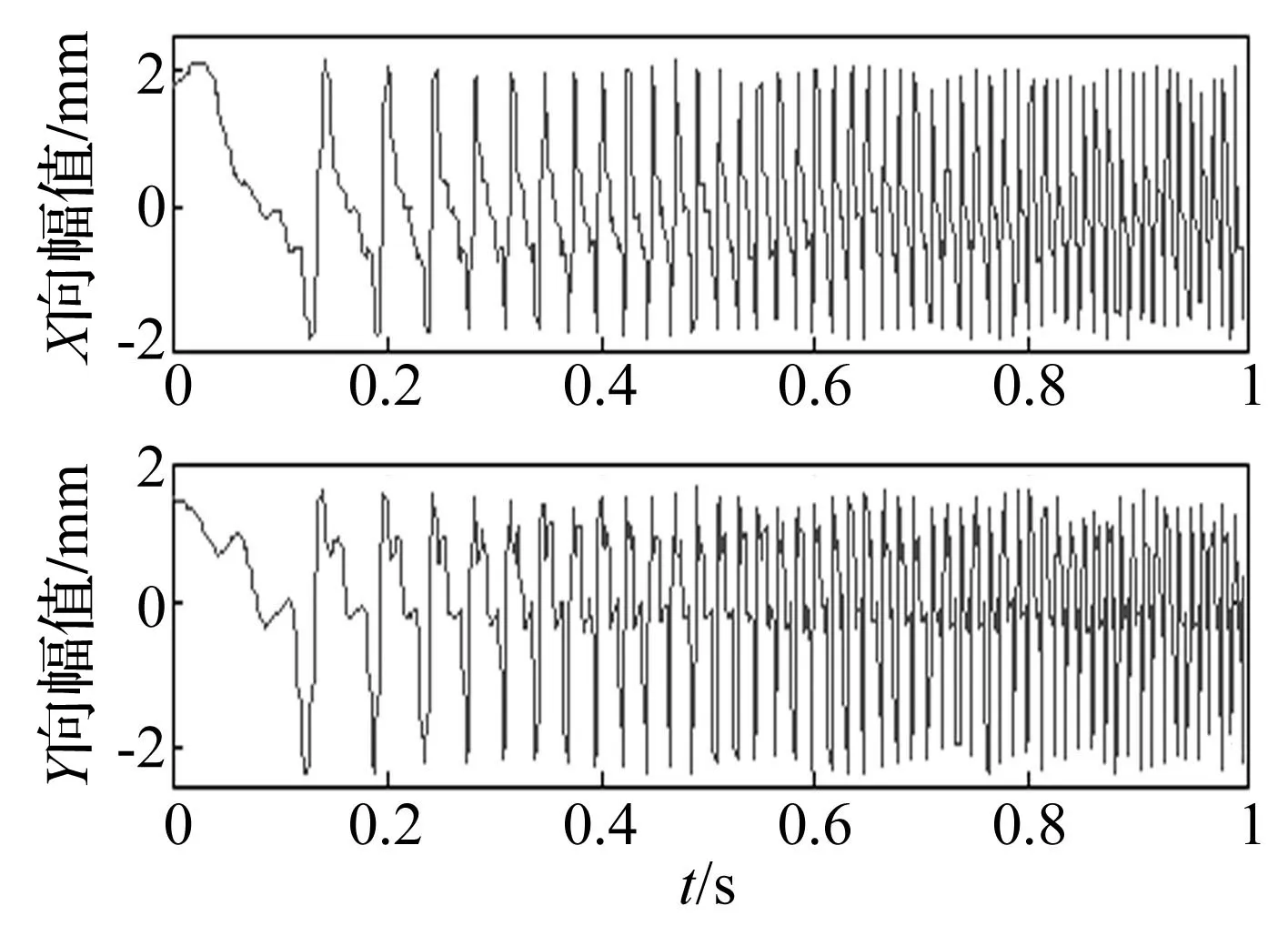
图1 X、Y方向振动信号

图2 重采样后X、Y方向振动信号

由于全息谱为对各倍频分析，而对图1中转速变化信号不能直接提取各倍频。因此对其以60的角域重采样频率进行基于三次样条插值的阶次重采样，截取前1 024点获得重采样角域稳定信号见图2。对重采样后X、Y方向信号进行阶次全息谱分析见图3。

图3 阶次全息谱

2 FT细化校正阶次全息谱

2.1 FT细化校正阶次全息谱方法

FFT+FT法[12]为在不增加采样点数情况下，先对信号进行FFT求得全景谱，再针对所需细化局部用连续FT细化校正计算获得局部细化、精度极高的频谱。本文提出FT细化校正阶次全息谱分析方法，先通过三次样条插值阶次跟踪获得等角度重采样的角域信号，再通过FT细化校正获得各阶次的精确幅值及相位信息，据幅值、相位值得出阶次全息谱图，具体计算流程为

(1) 基于三次样条插值的阶次跟踪重采样后获得角域采样频率Os阶，角域工频为1阶，角域平稳信号为x(n)，y(n)。

(2) 对x(n)，y(n)进行N点FFT分析，找出0～1阶间幅值最大的对应阶次作为分倍频分析阶次。计算出各倍频对应的阶次谱序列号k，按式(9)、(10)分别计算各倍频FT细化校正的起止频率f1，f2：

f1=(k-1)Os/N

(9)

f2=(k+1)Os/N

(10)

(3) 针对实际信号确定细化倍数D，一般取20～50之间。据f1，f2，D计算出阶次间隔Δf:

Δf=(f1-f2)/D

(11)

(4) 将{f1,f1+Δf,f1+2Δf,…,f1+lΔf=F2}分别代入式(12)、(13)，即可获得细化校正后阶次谱实、虚部值，取该阶次成分中幅值最大的作为该倍频幅值，即可分别求出X，Y方向各倍频校正后的幅值及相位Ax，ax，Ay，ay：

(12)

(13)

获得精确幅值、相位后，即可获得精确阶次全息谱图。FT细化校正阶次全息谱分析计算流程见图4。

图4 FT细化校正阶次全息谱流程

2.2 FT细化校正阶次全息谱仿真分析

对式(7)、(8)模拟信号进行FT连续细化校正阶次全息谱分析，得阶次全息谱图见图5。

对式(7)、(8)模拟信号进行阶次跟踪后基于比值校正法进行阶次全息谱分析，所得阶次全息谱见图6。

图6 比值校正法的阶次全息谱

由图3与图5、图6对比看出，不校正直接计算所得各倍频全息谱图区别较大。由表1看出，直接计算误差较大，因此计算全息阶次谱校正较重要。由图5、图6对比看出，在1X，3X，4X处基本相同，但在含密集谱的2X处，图5椭圆更扁平些且初始点位置不同，即两幅图离心率、初始相角不同。因密集频谱影响，直接比值校正法所得幅值、相位均有一定误差，反映到全息谱参数上即为正余弦系数与离心率不同。

由表1结果分析知，在2X处直接比值校正所得X，Y向正余弦参数结果与理论值绝对差分别为0.097 4，0.100 1，0.083 5，0.046 7，离心率绝对差为0.004 7，而FT细化校正法所得X，Y向正余弦参数结果与理论值绝对差分别为0.008 0，0.000 6，0.008 0，0.001 5，离心率结果基本相同。故FT细化校正法较比值校正法精度高，所得全息谱亦更精确。

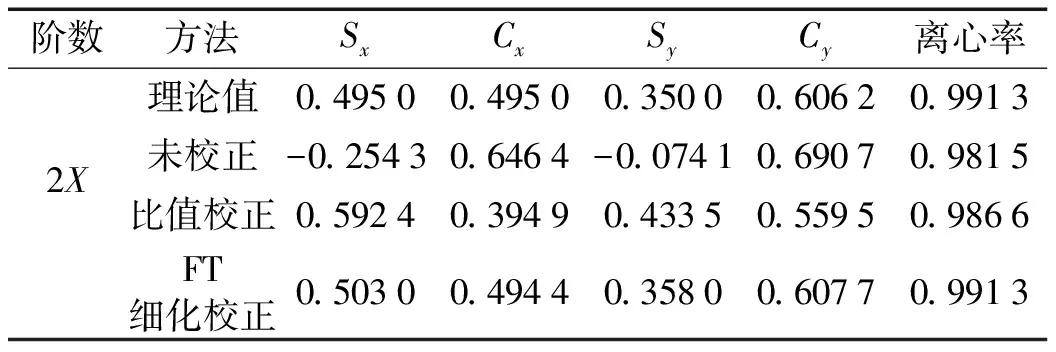
表1 2X阶次全息谱参数对比

3 应用实例

为验证本文方法的可行性与正确性，对转子实验台进行变速实验测试见图7，共采集4路信号，第1路为转速脉冲信号，第2路为X向振动信号，第3路为Y向振动信号，第4路为实验台振动加速度信号。

图7 柔性转子试验台

图8 转速脉冲信号

图9 X，Y方向振动信号

用512 Hz采样率进行同步采样，采集两组数据分别为正常、加偏心质量。加偏心质量测得的转速信号转换为标准脉冲信号见图8，加偏心质量测得的X，Y方向振动信号见图9。用采到的脉冲信号及X，Y向振动信号，据本文方法进行重采样，所得加偏心质量重采样后X，Y向信号见图10。

图10 重采样后X，Y方向振动信号

图13 阶次全息谱图

对原X，Y方向信号及重采样后X，Y方向信号进行频谱与阶次谱分析，其局部见图11、图12。由图11看出，转速频率在30～40 Hz波动，此时则不能选择工频，但重采样后即可较好提取到1阶频率。

对基于三次样条插值跟踪重采样信号直接进行阶次全息谱分析所得阶次全息谱见图13。用FT细化校正方法对重采样数据进行阶次全息谱分析，见图14。由图14看出，工频振幅较大，且为椭圆，而转子失衡时全息谱特征除工频椭圆外基本无其它倍频分量，工频椭圆形状较扁，可判断该转子失衡。而图13椭圆离心率较图14小，其椭圆不及图14扁，故图14故障特征表现更明显。为更好对比，对另采集的一组正常数据用本文方法同样分析获得阶次全息谱见图15。对比图14、图15更能说明对故障诊断的正确性。对图13～图15综合分析知，转速波动时基于三次样条插值重采样后用FT细化校正法进行阶次全息谱分析能较好确定转子的不平衡故障。

4 结 论

本文针对极端环境、特殊工况只能采集到转速不稳定振动信号、阶次全息谱分析精度不高问题，提出FT细化校正阶次全息谱分析，并对模拟信号及转子试验台采集信号分析，结论如下：

(1) 对非平稳信号进行阶次全息谱分析时，可用三次样条插值方法进行阶次重采样，FT细化校正法进行频谱计算，能在存在密集普情况下获得较精确的全息谱。

(2) 对转子试验台信号进行阶次全息谱分析与直接阶次谱分析对比充分说明该方法的有效性。通过与正常信号分析对比验证FT细化校正阶次全息谱分析方法能正确判断转子试验台故障。

[1]Goldman P, Muszynska A. Application of full spectrum to rotating machinery diagnostics[J]. Orbit, 1999, 20(1): 17-21.

[2]Sun Hui, Liu Da-you, Li Wen. The minimization of axiom groups of rough set [J]. Chinese Journal of Computers, 2002, 25(2): 201-209.

[3]Liu Shi, Qu Liang-sheng. A new field balancing method of rotor systems based on holospectrum and genetic algorithm [J]. Applied Soft Computing, 2008,8(2): 446-455.

[4]屈梁生,史东峰. 全息谱十年回顾与展望[J]．振动、测试与诊断,1998,18(4):235-242.

QU Liang-sheng, SHI Dong-feng. Holospectrum during the past decade: review & prospect[J]. Journal of Vibration, Measurement & Diagnosis, 1998,18(4):235-242.

[5]魏玉果,汤宝平,程发斌,等. 基于阶比跟踪的全息谱技术[J]. 重庆大学学报,2007,30(2):9-12.

WEI Yu-guo,TANG Bao-ping,CHENG Fa-bin,et al. Research of holospectrum technique based on order tracking [J].Journal of Chongqing University, 2007,30(2): 9-12.

[6]梅检民,陈祥龙,肖云魁,等. 基于稳健全息阶比谱提取微弱故障特征[J]. 振动与冲击,2012,31(12):49-53．

MEI Jian-min, CHEN Xiang-long, XIAO Yun-kui，et al. Weak fault characteristic extraction based on steady holographic-order spectrum[J]. Journal of Vibration and Shock, 2012, 31(12): 49-53．

[7]Liu Shi.A modified low-speed balancing method for flexible rotors based on holospectrum[J]. Mechanical Systems and Signal Processing,2007, 21: 348-364.

[8]Ding Kang, Yang Zhi-jian. Improvement and anti-noise performance analysis of window-length changing phase different correction[J]. Journal of South China University of Technology, 2007, 10(35): 210-213.

[9]Shi Dong-feng, Qu Liang-sheng, Bao Ming. Instantaneous purified orb it: a new tool for analysis of nonstationary vibration of rotor system [J]. Rotating Machinery,2001,7(2):105-115.

[10]Fyfe K R, Munck E D S. Analysis of computed order tracking[J].Mechanical Systems and Signal Processing,1997,11(2): 187-205.

[11]汤宝平，何启源，魏玉果，等. 基于角加速度的复合计算阶次跟踪方法[J]机械工程学报，2008，44(8)：143-147．

TANG Bao-ping, HE Qi-yuan, WEI Yu-guo, et al. Hybrid computed order hacking method based on angular acceleration [J]. Chinese Journal of Mechanical Engineering, 2008, 44(8):143-147．

[12]丁康, 朱文英, 杨志坚, 等. FFT+FT 离散频谱校正法参数估计精度[J]. 机械工程学报, 2010 ,46(7): 68-73.

DING Kang, ZHU Wen-ying, YANG Zhi-jian, et al. Parameter estimation accuracy of FFT and FT discrete spectrum correction[J]. Journal of Mechanical Engineering, 2010, 46(7): 68-73.