基于量子叠加态参数估计的机械振动信号降噪方法
2014-09-06陈彦龙张培林王怀光
陈彦龙,张培林,王怀光
(军械工程学院 七系,石家庄 050003)
机械状态监测有效方法为振动信号分析,而现场采集的振动信号会受噪声干扰,直接影响机械设备状态监测。小波分析在振动信号降噪中得以广泛应用,通常假设小波分解系数满足高斯分布,但小波压缩特性使小波系数概率密度分布较高斯分布在零值位置更尖,并在分布两端呈明显拖尾趋势,故设小波分解系数满足高斯分布所得结论并不准确。陶新民等[1]用广义高斯分布分析轴承振动信号多尺度小波分解系数的统计特征,实现轴承故障诊断。张志刚等[2]据机械振动信号有效小波系数统计分布进行拉普拉斯建模,对主减速器中齿轮故障信号进行有效降噪。
小波变换中,双数复小波(DTCWT)具有近似平移不变性等性质[3],信号分析效果更好。本文将用DTCWT实现一维机械振动信号的小波变换。而多数研究均假设信号双树复小波系数的实、虚部独立分布,未考虑信号虚、实部间关系,若采用二维广义高斯分布及二维拉普拉斯分布[4]对实、虚部小波系数建模,则参数估计复杂,需大量数值计算,较难实现。为此,本文基于二维正态分布提出含可变参数的联合概率密度分布。并受文献[5]QSP基本理论启发,借鉴量子叠加态概念,对信号进行分析、处理:① 对信号DTCWT小波系数建模,建立含可变参数的联合概率密度分布;② 据贝叶斯极大后验估计(MAP)准则,结合父-子代小波系数尺度间相关性,导出基于叠加态参数估计的自适应收缩函数,实现一维机械振动信号降噪。结果表明,该方法对机械振动信号降噪性能良好。
1 DTCWT小波系数联合概率密度
1.1 二维概率密度函数
研究信号DTCWT小波系数分布规律,建立数学模型,有助于实现信号降噪,由含噪信号中估计出原信号。对含加性高斯白噪声信号y(t)进行小波变换,由小波变换线性性质,有:
Y=X+N
(1)
式中:Y=Yr+iYi为含噪信号复小波系数;X=Xr+iXi为无噪信号复小波系数;N=Nr+iNi为噪声复小波系数。
高斯白噪声经小波变换后仍为同方差的高斯白噪声。用拉普拉斯函数与广义高斯函数建立小波系数模型,但直接利用二维拉普拉斯分布及广义高斯函数计算形式复杂,模型参数估计难以实现,通用性不强。为提高双树复小波系数分布模型通用性,本文基于二维正态分布提出带可调参数k的概率密度函数(PDF),设无噪信号小波系数真实概率密度分布为f0(xr,xi),数学模型为
(2)
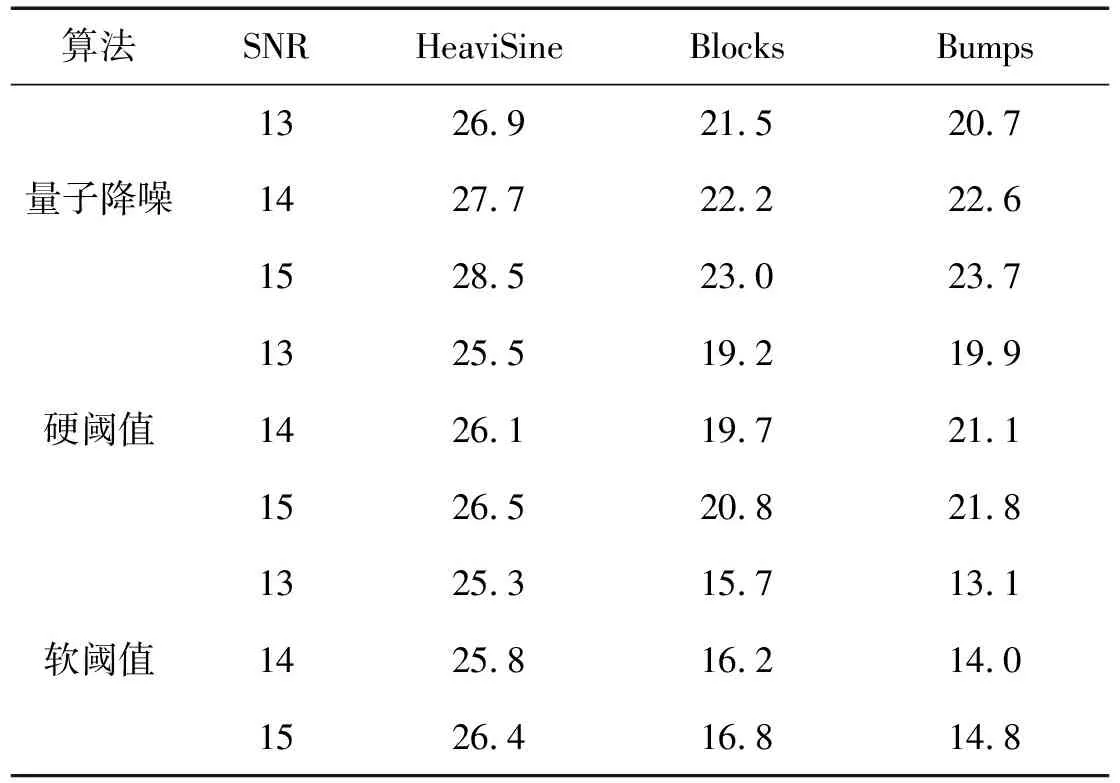
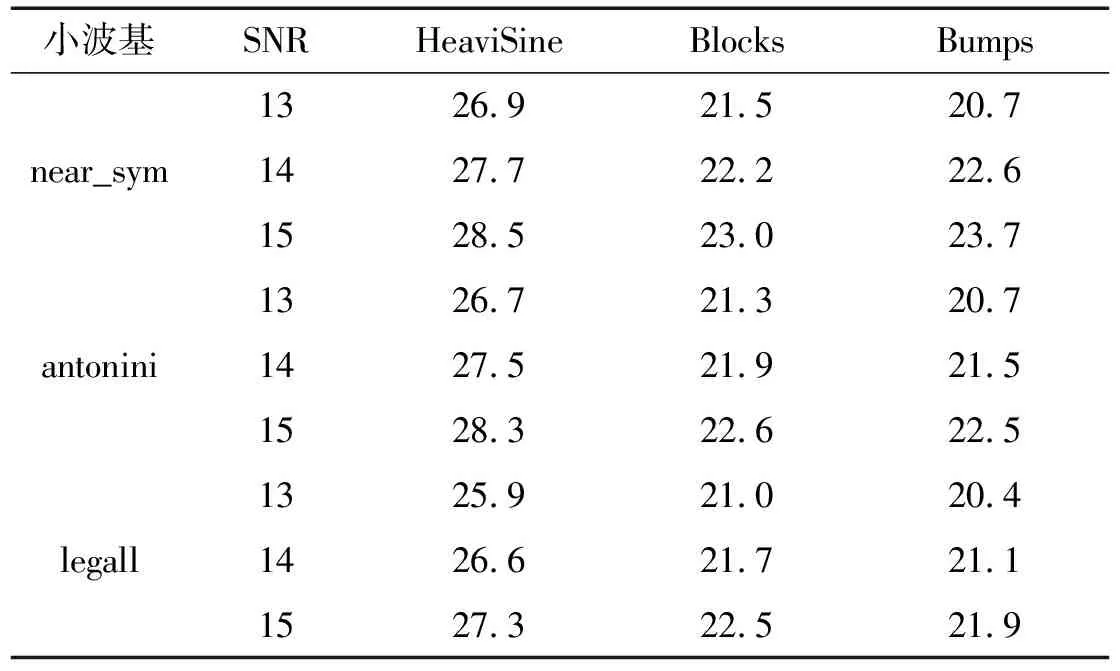
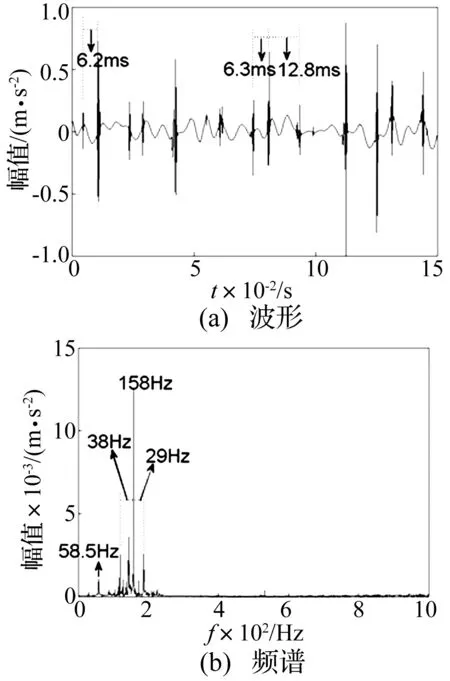
式中:-∞ 分析联合概率密度函数可获得边缘密度概率密度函数,即双树复小波系数实、虚部分布规律,为参数估计提供依据。Xr边缘概率密度函数为 (3) 由于 (4) 于是 (5) 令 (6) 则有 (7) 即 (8) 同理,Xi的边缘概率密度函数为 (9) 由以上推导发现,k为小波系数概率密度函数的关键参数,其取值关系概率密度函数形状及拟合精度。据各尺度中双树复小波系数二维概率密度函数与边缘概率密度函数最小均方差共同确定k值: k1=E[f0(xr,xi)-f(xr,xi)]2 (10) k2=E[f0Xr(xr)-fXr(xr)]2 (11) k3=E[f0Xi(xi)-fXi(xi)]2 (12) (13) 式中:f0(xr,xi),f0Xr(xr),f0Xi(xi)为实际分布;f(xr,xi),fXr(xr),fXi(xi)为曲线拟合分布。 拟合过程中,据双树复小波边缘概率密度函数fXr(xr),fXi(xi)的PDF最大值为Pr,Pi求出σr,σi: (14) (15) k的误差精度为0.1时,双树复小波系数分布拟合精度不够;k的误差精度为0.001时,分布拟合精度与k的误差精度0.01时接近。综合考虑分布拟合精度与计算速度,设k值的误差精度为0.01。 (16) 式中:α,β为一对复数,称量子态概率幅,且满足 (17) 贝叶斯理论在小波降噪中得到较好应用。通过贝叶斯理论,可实现对小波系数收缩,降低噪声。在贝叶斯统计理论中,最大后验估计(MAP)为常用方法。本文据含噪信号双树复小波系数Y,获得使后验概率密度函数PX|Y取最大值的无噪小波系数X。此处以实部边缘概率密度函数为例: (18) 据贝叶斯原理: (19) 设噪声小波系数服从均值为0、标准差为σn、相关系数ρn=0的高斯分布。据式(5)及噪声模型,式(19)可写为 (20) 式中:f(Xr)=lnpXr(Xr)。 对式(20)求Xr的导数,并令其为0,得: (21) 据Yr与Xr的边缘概率密度函数,经推导,Xr的估计式为 (22) (23) 基于量子叠加态原理展开分析,给出基于量子叠加态的参数估计算法,并对式(22)中关键参数进行估计。信号、噪声在小波域奇异特性不同,信号突变点处小波系数幅值明显增大,而噪声小波系数幅值将随尺度的增加迅速减小[7]。因此可据相邻尺度的小波系数乘积减少噪声。 对双树复小波系数而言,若父系数模较大,则对应位置的子系数同样具有较大模值。父-子代小波系数模的乘积表达式为 (24) (25) (26) (27) (28) 当前位置j量子叠加态信号方差σ估计式为 (29) 式中:Wj为以当前系数Y(s,j)为中心的子窗口;Mj为窗口中系数个数。取第s尺度上邻域窗W(j)宽度为Ms=2s+1-1。 当前位置j量子叠加态信号期望u估计式为 u(Yj)=u(Xj+Nj)=u(Xj)+u(Nj) (30) 由于 u(Nj)=0 (31) 故 u(Xj)=u(Yj) (32) 本文所提基于量子叠加态的小波系数估计方法,能较好利用小波系数尺度间相关性。将式(28)、(29)代入式(22)知,对小波系数Y(s,j),若其量子叠加态表明有用信号出现概率大,收缩因子自适应变大;反之,收缩因子自适应变小,该自适应收缩函数有利于噪声抑制。 本文的信号降噪算法步骤为: (1) 利用DTCWT实现含噪信号y(t)的小波分解; (2) 据各尺度高频小波系数二维概率密度函数及边缘概率密度函数,拟合确定k值; (4) DTCWT逆变换获得降噪信号。 分别采用HeaviSine、Blocks、Bumps信号[9]验证本文模型降噪的可行性及有效性。信号长度2 048点。对3种信号分别加入高斯白噪声,使含噪信号的信噪比分别为13 dB,14 dB,15 dB,用本文方法降噪,并用5层分解及重构。对去噪效果,采用信噪比(SNR)进行评价。若在原始信号y(t)中加入不同噪声n(t),降噪后所得信号为d(t),单位为dB,则信噪比定义为 SNR=10lg(Pd/Pn) (33) 式中:Pd为原始信号功率;Pn为噪声功率。信号噪声由原始信号y(t)减去降噪信号d(t)获得: (34) 用传统软、硬阈值降噪法进行效果对比,阈值λ为 (35) 表1为不同算法降噪结果。由表1看出,基于量子叠加态参数估计的信号降噪模型降噪效果最好,极大提高了信号的信噪比。表2为不同双树复小波基下本文降噪方法降噪效果。随小波基变化,仍能取得良好降噪效果,表明本文方法适用性良好。 表1 不同算法降噪结果 表2 不同双树复小波基降噪结果 采用某新型机械设备的综合传动装置进行研究,在轴承内圈加工1×0.2 mm划痕。采集加速度振动信号,实测转动速度1 830 r/min,在3档档位上测量,传感器安装在对应轴承位置箱盖上方。内圈故障理论频率为158 Hz。轴承故障见图1。采样频率12 kHz,采样时间1 s。为便于比较,取2 048点进行分析。故障信号波形见图2,由频谱中看出,故障频率淹没在噪声频率中。 图1 机械综合传动装置 不同降噪方法结果比较见图3~图5,运算时间见表3。 (1)波形分析。由图形看出,软、硬阈值降噪方法去除大量噪声的同时也去除有用信号,使降噪后脉冲周期不准确;而基于量子叠加态的参数估计降噪方法所得脉冲周期准确,且故障脉冲较软、硬阈值降噪保留更多,有益故障判断。通过测量,降噪后信号明显存在间隔6.3 ms冲击,对应于内圈故障频率158 Hz,可确定为滚动轴承内圈出现故障。因此,量子降噪方法使噪声大部分被消除的同时,较好保留了轴承故障冲击特征,脉冲波形完整。 图2 含强噪声故障信号 (2)频谱分析。比较降噪后信号频谱,小波阈值降噪后,158 Hz频率突出,但调制频率不准确,不符合轴承内圈故障频率特点,小波阈值降噪方法未能达到较好降噪效果;采用基于量子叠加态的参数估计降噪方法处理后,频谱中158 Hz频率突出,且存在明显边带,转频(30.5 Hz)及二倍频(61 Hz)、三倍频(91.5 Hz)明显,符合轴承内圈故障频谱特点。 图5 软阈值降噪消噪结果 表3 不同算法运算时间 (3) 运算效率。据表3,量子降噪时间多于软硬阈值降噪法,但运算时间仍较短,为快速降噪方法。 (1) 基于二维正态分布带可调参数k的概率密度函数考虑双树复小波系数实、部关系,k值计算过程兼顾二维概率密度函数与边缘概率密度函数,使该分布模型自适应更强。 (2) 基于量子叠加态的机械振动信号降噪方法,充分利用DTCWT的平移不变性及量子降噪模型可捕获小波系数尺度间相关性特点,可获得较常规小波降噪方法更高的信噪比,能有效抑制高斯白噪声。 (3) 本文所提降噪方法可有效保留轴承冲击信号特征,据其周期性冲击对应的特征频率,可对轴承故障进行故障识别,为强背景噪声下机械故障信息提取提供新途径。 [1]陶新民,徐晶,杜宝祥,等. 基于小波域广义高斯分布的轴承故障诊断方法[J]. 机械工程学报, 2009, 45 (10): 61-67. TAO Xin-min, XU Jing, DU Bao-xiang, et al. Bearing fault diagnosis based on wavelet-domain generalized gaussian distribution[J]. Journal of Mechanical Engineering, 2009, 45(10): 61-67. [2]张志刚,周晓军,宫燃,等. 小波域局部Laplace 模型降噪算法及其在机械故障诊断中应用[J]. 机械工程学报, 2009, 45 (9): 54-57. ZHANG Zhi-gang,ZHOU Xiao-jun,GONG Ran, et al. Denosing algorithm based on local laplace model in wavelet domain and its application in mechanical fault diagnosis[J]. Journal of Mechanical Engineering, 2009, 45 (9): 54-57. [3]Nelson J D B, Kingsbury N G. Enhanced shift and scale tolerance for rotation invariant polar matching with dual-tree wavelets[J]. IEEE Trans on Image Processing,2011,20 (3): 814-821. [4]Eltoft T, Kim T, Lee T W. On the multivariate laplace distribution[J]. IEEE Signal Processing Letters,2006,13(5): 300-303. [5]Eldar Y C, Oppenheim A V. Quantum signal processing[J]. IEEE Signal Process Mag, 2002, 19 (6): 12-32. [6]李盼池, 宋考平, 杨二龙. 基于量子门线路的量子神经网络模型及算法[J]. 控制与决策, 2012, 27 (1): 143-146. LI Pan-chi, SONG Kao-ping, YANG Er-long. Quantum neural networks model and algorithm based on quantum gates circuit[J]. Control and Decision, 2012, 27 (1): 143-146. [7]Zhang L, Bao P. Edge detection by scale multiplication in wavelet domain[J]. Pattern Recognition Letters,2002,23(14): 1771-1784. [8]付晓薇, 丁明跃. 基于量子概率统计的医学图像增强算法研究[J]. 电子学报,2010,38(7):1590- 1596. FU Xiao-wei, DING Ming-yue. Research on image enhancement algorithms of medical images based on quantum probability statistics[J]. Acta Electronica Sinica, 2010, 38 (7): 1590-1596. [9]Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of American Statistical Association, 1995, 90 (432): 1200-1224.1.2 边缘概率密度函数
1.3 可调参数k确定
2 量子叠加态参数估计模型
2.1 量子叠加态
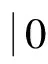
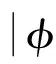
2.2 贝叶斯MAP估计器
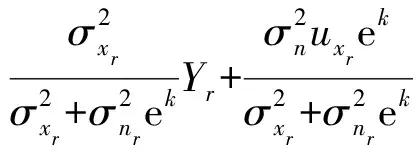
2.3 量子叠加态参数估计
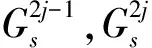
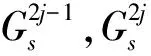

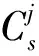
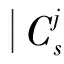
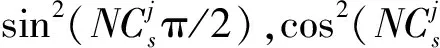
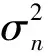
3 降噪算法步骤
4 仿真与实际信号验证
4.1 仿真信号
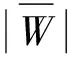
4.2 实际信号



5 结 论
