集成相对位移自传感磁流变阻尼器性能优化
2014-09-06白先旭王代华
白先旭,王代华
(1. 重庆大学 光电工程学院,重庆 400030;2. 重庆大学 光电技术及系统教育部重点实验室,重庆 400030)
目前,磁流变(Magnetorheological, MR)阻尼器的可控阻尼性能及应用该半主动可控器件系统性能被优化已获得广泛认可。而为充分利用MR阻尼器可控阻尼性能,半主动系统需安装与主动系统相同动态响应传感器[1]。不仅降低基于MR阻尼器的半主动系统可靠性,且使系统结构复杂化、增加安装空间、提高系统成本。对此,实现具有动态响应自传感功能的MR阻尼器势在必行。Wang等[2]提出并研究集成相对位移自传感MR阻尼器(IRDSMRD),而研究中发现,IRDSMRD虽能实现相对位移传感功能与可控阻尼力功能的集成,但为实现在MR阻尼器中集成相对位移传感器(IRDS),IRDSMRD阻尼力性能会受影响[3-4],随用于IRDSMRD的励磁电流增加,即随IRDSMRD的阻尼力增加,IRDS传感器输出信号逐渐表现出非线性特性。
对IRDSMRD性能优化,需对MR阻尼器性能及IRDS性能优化。即IRDSMRD阻尼力与IRDS传感性能应协调优化。MR阻尼器性能优化主要对MR阻尼器几何尺寸优化。Rosenfeld等[5]对体积一定的MR阻尼器进行结构尺寸优化且对不同功率密度对无量纲厚度与阻尼因子影响进行研究。Nguyen等[6]对半主动悬架用MR阻尼器最大阻尼力、动态阻尼力范围及感应时间常数利用ANSYS软件进行优化,给出对设计MR阻尼器有指导意义结论。而迄今鲜有阻尼力性能与IRDS性能同时优化研究。设计、开发自传感MR阻尼器时,如何优化IRDSMRD相互影响的IRDS传感性能及MR阻尼器可控阻尼力性能为须解决的问题。
实际上,将同时优化IRDSMRD阻尼力性能与IRDS传感性能可视为多目标优化问题[7]。Pareto优化方法可用于寻找相互制约目标的最优协调。Paplia等[8-9]利用Pareto优化圆形压电执行器体积量及共振频率,并对压阻麦克风压强灵敏度及电子噪声底限进行协调优化。关新春等[10]用Pareto对MR阻尼器的阻尼力及动态阻尼力范围进行协调优化。由此,Pareto优化方法可用于IRDSMRD阻尼力与IRDS传感性能优化。据文献[3],IRDSMRD阻尼力及IRDS线性度同时优化可通过优化IRDSMRD结构参数实现,亦可通过降低作用于IRDSMRD的励磁电流(对同一IRDSMRD而言即为作用磁动势)实现。Wang等[4]通过优化IRDSMRD结构参数实现对IRDSMRD的最大可控阻尼力及IRDS线性度协调优化。本文为对IRDSMRD性能(阻尼力性能、IRDS传感性能)优化,提出基于Pareto优化原理、对体积一定的IRDSMRD关键参数(含结构参数及作用磁动势)进行关于目标函数为阻尼力及IRDS的线性度优化方法。对影响IRDSMRD阻尼力与IRDS线性度的磁通回路磁特性建模、分析并建立受IRDSMRD关键参数影响的IRDS线性度与IRDSMRD阻尼力数学模型,并利用Pareto优化原理对IRDSMRD性能协调优化。
1 IRDSMRD的原理与数学模型
1.1 IRDSMRD的结构与原理
文献[2]的IRDSMRD结构原理与3D拆装分别见图1(a)、(b)。IRDSMRD电路系统原理示意及系统实物分别见图2(a)、(b)。IRDSMRD结构材料属性与基本参数见表1。由图1,IRDSMRD利用在高导磁活塞上均匀绕制励磁线圈同时充当MR阻尼器的励磁线圈及IRDS的励磁线圈,利用在不导磁的缸筒上均匀绕制感应线圈作为IRDS感应线圈,置于高导磁缸体罩内。由图2、表1,通过叠加电路将励磁电流与载波信号叠加后作用于IRDSMRD活塞的励磁线圈,产生直流励磁磁场及与载波信号同频的谐波磁场叠加磁场,并沿IRDSMRD主磁通回路闭合。由励磁线圈产生的磁场使缸体罩内不导磁缸体上均匀绕置的感应线圈获得感应电压,该电压由与载波信号同频的谐波电压信号及励磁电流作用于运动的活塞上励磁线圈产生的直流励磁场而产生的感应信号两部分组成。当活塞相对缸体运动时,感应线圈中谐波电压信号被活塞与缸体间相对位移实现幅度调制。通过解调感应线圈的感应电压可获得活塞相对缸体位移,实现IRDS。由于MR液流间隙位于主磁通回路中,由励磁电流产生的磁场将对MR阻尼器实现励磁,即实现MR阻尼器与动态传感器功能集成。
为确保IRDSMRD具有较好的阻尼力性能及位移传感性能,所选材料应确保IRDSMRD励磁磁场起于阻尼器活塞、穿过MR液流间隙、缸体及感应线圈,沿高导磁缸体罩、上端盖、活塞杆,返回活塞形成的闭合工作磁回路(即主磁通回路)。为使磁场尽量能沿主磁通回路,活塞杆、活塞头、上端盖、缸体罩选高导磁率的金属软磁材料(20#钢),而缸体、励磁线圈盖及缸体下端盖选不导磁的金属材料(不锈钢),材料属性见表1。

图1 IRDSMRD原理与结构
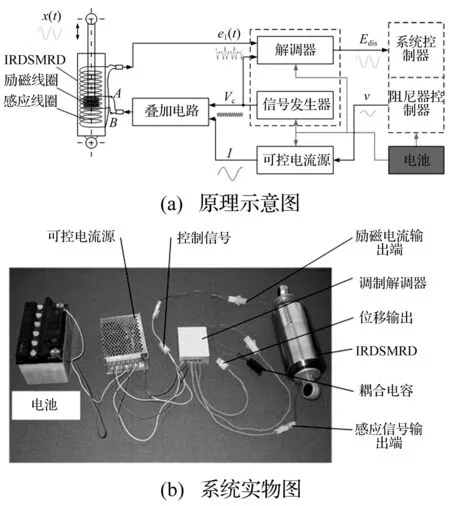
图2 IRDSMRD电路系统

表1 IRDSMRD结构材料磁特性及参数值
1.2 IRDSMRD数学模型
1.2.1磁通回路模型
IRDSMRD磁通回路及等效磁路模型见图3,其中各符号含义及尺寸见表2。
据磁路Kirchhoff第二定理得:
PI=NI=φIR
(1)
式中:PI为由幅值为I的励磁电流作用于匝数为N的励磁线圈产生的磁动势;φI为磁动势PI在磁通回路中产生的总磁通量;R为主磁通回路总磁阻,据图3,R可表示为
R=Rr1+Rl2+Rh+RL+Rg1+Rg2+Rg3
(2)
式中:Rr1,Rl2,Rh,RL,Rg1,Rg2,Rg3为在IRDSMRD主磁通回路中活塞杆、上端盖、缸体罩、活塞头、MR液流间隙(对应于活塞头高度)、不导磁缸体及感应线圈磁阻,可分别表示为

(3)
式中:μ0为真空磁导率(表1);x(t)为活塞相对缸体位移,起点为IRDSMRD行程零点(图1(a)、图3(a));l1,l2,L分别为励磁线圈盖高度、上端盖厚度、活塞头高度;r1,r2,rp分别为活塞杆半径、中心孔半径、活塞头半径;g1,g2,g3分别为圆环形液流间隙厚度、缸体厚度、感应线圈厚度;h为缸体罩厚度;μr1,μl2,μh,μL,μg1,μg2,μg3分别为活塞杆、上端盖、缸体罩、活塞头、MR液流间隙(对应于活塞头高度)、不导磁缸体及感应线圈磁导率。本文将不导磁缸体及感应线圈磁导率近似于空气,即μg2=μg3=μair=1。
磁动势PI在IRDSMRD磁通回路中产生的总磁通量φI可表示为
φI=BaAa
(4)
式中:Aa为主磁通回路中任意处截面积;Ba为Aa处磁感应强度。
据文献[4]及式(2)、(3),金属软磁性材料(20#钢)磁导率随磁动势PI的变化微小变化。据式(4)、表2可得活塞杆、上端盖、缸体罩、活塞头及MR液流间隙处MR液磁感应强度及磁导率μr1,μl2,μh,μL,μg1。
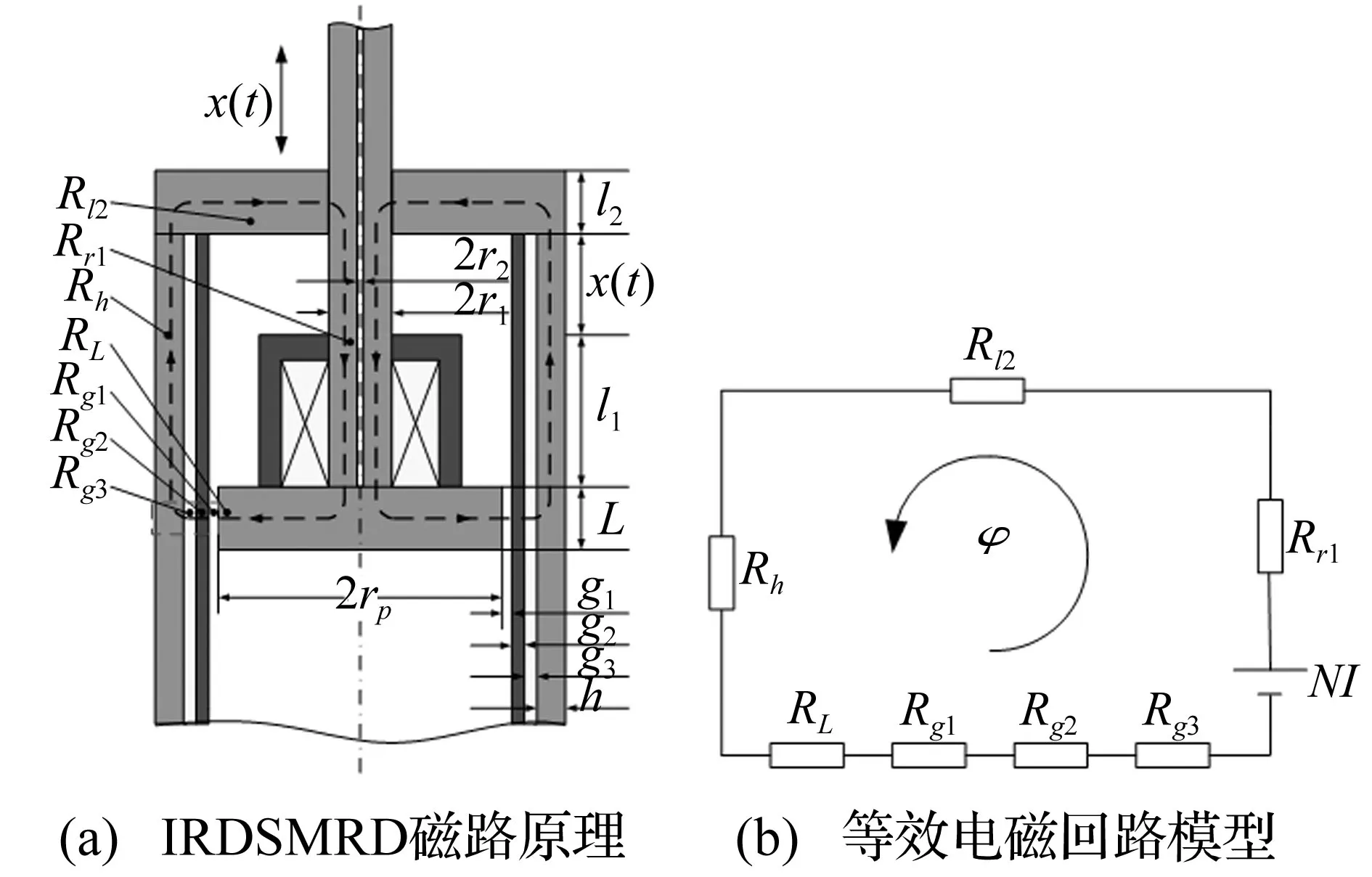
图3 IRDSMRD电磁回路

表2 IRDSMRD结构尺寸
1.2.2 IRDS线性度
IRDS传感器所得信号与感应线圈上感应谐波电压e1(t)相关[3]。据IRDSMRD原理,载波信号作用于IRDSMRD励磁线圈上,在感应线圈上被激活的磁链总数ψc(t)可表示为
(5)
式中:φc(t)为载波信号Vc在IRDSMRD主磁通回路产生的主磁通量;k为IRDSMRD缸体单位长度上绕感应线圈匝数;Pc为载波信号作用于IRDSMRD励磁线圈产生的磁动势。
感应线圈上磁通量为余弦信号较载波信号提前π/2[2],有:
(6)

对式(6)两端微分得IRDSMRD感应线圈上感应谐波电压e1(t)为
(7)

据调制解调原理,在式(7)两端同乘参考信号得:
(8)
对式(8)信号低通滤除频率2fc信号(图2(a)),得:
(9)
据文献[4]及式(1)~式(3),IRDSMRD磁通回路总磁阻R在磁动势PI影响下发生轻微变化。因此,由式(9)可知解调后信号Edis会受IRDSMRD主磁通回路磁阻R及IRDSMRD活塞位移量x(t)影响。而相对位移量x(t)对Edis影响无法避免。为IRDS原理误差,且相对总磁阻R对Edis影响而言较小,本文忽略x(t)变化对Edis影响。定义IRDS线性度(即非线性误差)为
(10)
式中:E0为主磁通回路各处磁导率均为初始值时相对位移,即Edis初始值。
据式(1)~式(3)、(9)、(10),IRDS线性度会受作用于IRDSMRD上磁动势及IRDSMD磁通回路上结构参数影响。据式(9),式(10)可改写为
(11)
式中:R0为主磁通回路初始总磁阻,与E0对应。
对IRDS线性度产生影响的关键参数为IRDSMRD活塞头高度L[4]。据式(1)~式(3),作用于IRDSMRD上磁动势即为导致IRDS非线性主要原因,本文设作用于IRDSMRD上励磁电流最大值已确定,即磁动势PI为IRDSMRD活塞上绕励磁线圈匝数N已确定。因此,可定义向量X=[N,L]T为决定IRDS线性度主要变量。
1.2.3 阻尼力
IRDSMRD阻尼力由粘滞阻尼力与 MR液流间隙受磁场作用产生的剪切屈服应力(即场控阻尼力)组成[11],由图1、图3(a),IRDSMRD阻尼力可表示为
(12)
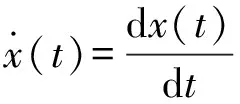
剪切-有效磁感应强度Bg1可表示为
(13)
式中:φg1为主磁通量。考虑MR液流间隙附近存在磁力线扩散,存在近似关系:
φg1≈0.45φl
(14)
据文献[4]及式(12),IRDSMRD阻尼力主要由活塞头高度L与导致MR液产生剪切屈服力的磁动势PI决定。最大励磁电流一定时,磁动势PI由IRDSMRD活塞上所绕励磁线圈匝数N确定。因此向量X=[N,L]T可决定IRDSMRD的可控阻尼力变量。
1.3 数值仿真
据上述,因其它参数(上端盖厚度、缸体外罩厚度)对IRDS线性度影响及阻尼力影响有限,而活塞杆半径(缠绕励磁线圈部分)及活塞头高度为主要影响因素,其中活塞杆半径对阻尼力、IRDS线性度而言越大越好,故取上限(13.0 mm)。本文在不同活塞头高度L、励磁线圈匝数N对阻尼力及IRDS线性度影响程度进行数值仿真。具有不同励磁线圈匝数N及活塞头高度L时IRDSMRD阻尼力性能及IRDS传感器性能数值仿真结果见图4。由图4看出,励磁线圈匝数N恒定时,随活塞头高度L逐渐增加,IRDSMRD阻尼力亦逐渐增加,IRDS线性度逐渐恶化;活塞头高度L恒定时,随励磁线圈匝数N逐渐增加,IRDSMRD阻尼力逐渐增加,而IRDS线性度逐渐恶化。因此可认为,通过优化IRDSMRD关键参数优化阻尼力性能(或IRDS传感性能)时,IRDSMRD的IRDS传感性能及阻尼力性能相互制约。
由图4看出,励磁线圈匝数N、活塞头高度L同超一定范围时,N与L对IRDSMRD性能产生条件限制,此时无解。
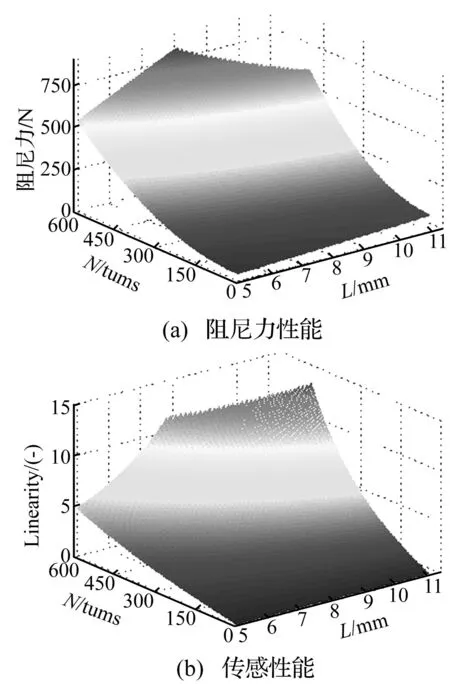
图4 不同励磁线圈匝数、活塞头高度时IRDSMRD性能
2 优化设计
IRDSMRD最大可控阻尼力与IRDS线性度优化可通过优化IRDSMRD关键结构参数实现,也可通过降低作用于IRDSMRD的磁动势(即在最大励磁电流一定时优化励磁线圈匝数N)实现[3]。而通过优化IRDSMRD的关键结构参数实现对IRDSMRD最大可控阻尼力、IRDS线性度协调优化[4]。本文通过优化IRDSMRD作用磁动势PI与活塞头高度L实现对目标函数分别为IRDSMRD最大可控阻尼力、IRDS线性度协调优化。
2.1 设计变量
由于IRDSMRD最大可控阻尼力、IRDS线性度均关于励磁线圈匝数N(作用于IRDSMRD电流I最大值为定值时)、活塞头高度L函数且之间存在相互约束关系,采用Pareto优化对二者协调优化。在作用于IRDSMRD电流I最大值为定值时优化IRDSMRD阻尼力及IRDS传感性能,取优化变量为励磁线圈匝数N及活塞头高度L,即向量X=[N,L]T为优化变量。
2.2 约束条件
优化参数边界及操作要求为
(1) 设计变量下边界(LB)、上边界 (UB):考虑IRDSMRD实际尺寸,设计变量边界可表示为
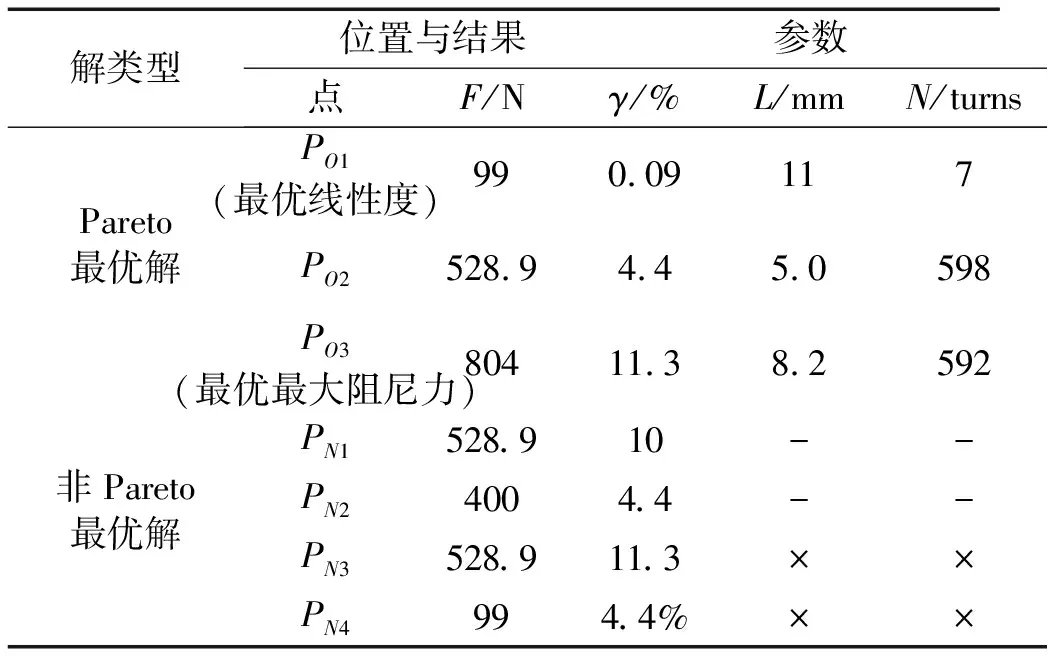
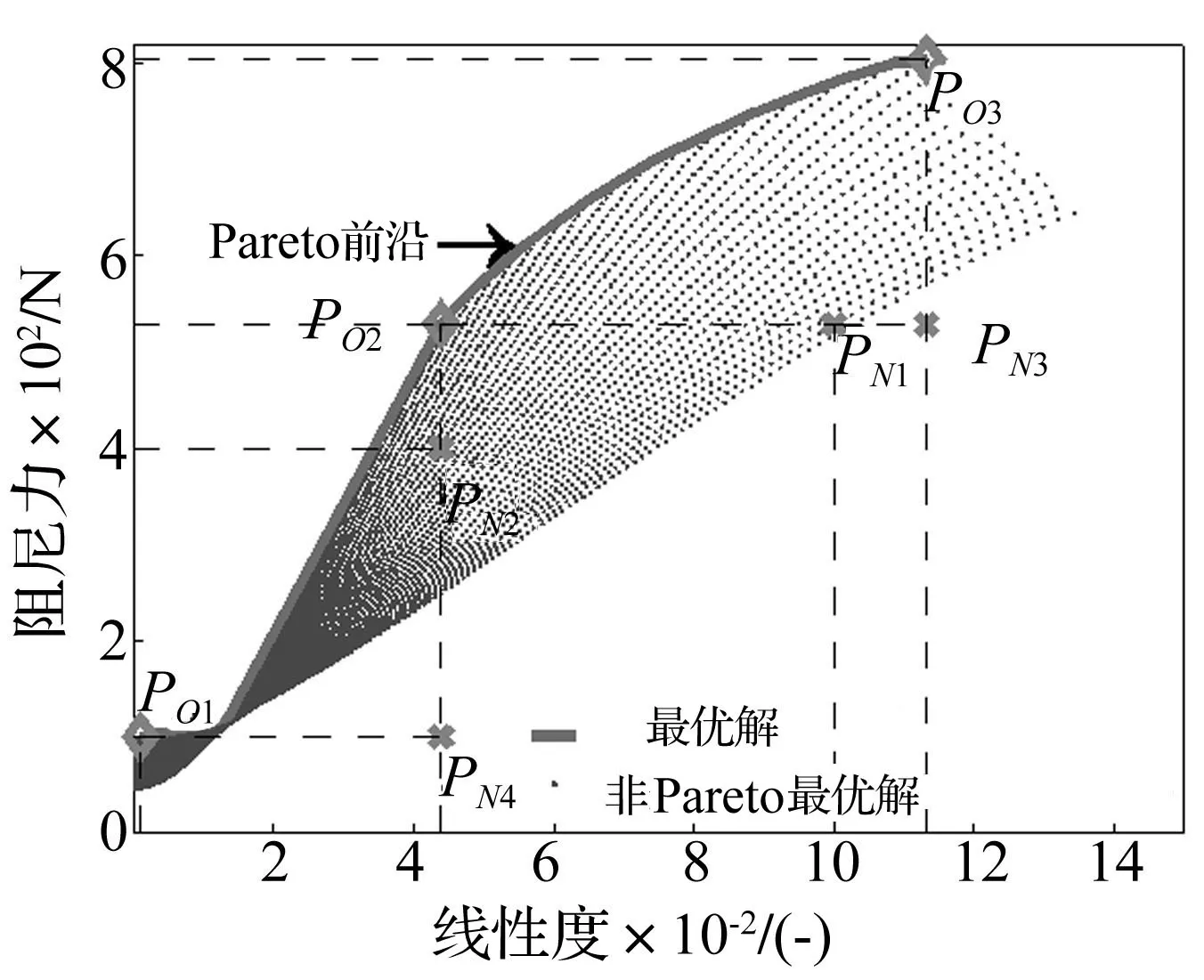
XLB (15) 式中:XLB=[0.5]T,XUB=[60 011]T为IRDSMRD优化变量最小、最大值。 (2) 磁感应强度:IRDSMRD选材的磁感应强度所受约束可表示为 (16) 式中:BsMRF,Bs20分别为MR液、20#钢饱和磁感应强度;Ba20为IRDSMRD结构零件(20#钢,表1)。 (3) 励磁电流(I):作用于IRDSMRD的励磁线圈上电流最大为1.2 A,即 (17) 优化问题可视为优化目标函数FO(X),表示为 (18) 实现IRDSMRD阻尼力最大化目标的同时,IRDS线性度会降低,即实现IRDSMRD阻尼力最大化目标与实现IRDS线性度最优目标相互制约。若不考虑IRDS线性度约束,IRDSMRD阻尼力可被提高至较大范围(IRDS线性度较差)。IRDS线性度亦为IRDSMRD重要性能,故将IRDS线性度与IRDSMRD阻尼力考虑为多目标函数优化问题较正确。 Pareto优化常被用于多目标优化,为典型的寻找能使每个函数均在约束条件内的最优折中方法。称多目标优化问题Pareto最优解在目标函数空间中的表现形式为Pareto最优边界(Pareto前沿)。对相互约束的多目标函数,在Pareto前沿找不到能使所有目标变好的解。为同时优化IRDSMRD阻尼力及IRDS传感性能,利用Pareto优化方法原理,据式(18)构建总体目标函数f1=F(X)并增加限制其它目标函数fj=γ(X)的函数Cj=γlimj(X)(为不同IRDS线性度预置值)以评价多目标函数特性,可写为 (19) 通过用不同Cj获得Pareto最优点集(即在除去此点之外找不到能使目标函数更优的点),从而获得Pareto前沿。 利用MATLAB软件对IRDSMRD阻尼力及IRDS线性度进行关于向量X(即参数N,L)在上下边界内等间距逐点计算,结果见图5。由图5看出,所有Pareto最优解组成Pareto前沿。该前沿上PO1点为典型解,即IRDS线性度最优解,IRDSMRD阻尼力较小。Pareto前沿上PO3点也为典型解,即IRDSMRD最大阻尼力及较差IRDS线性度。PO2点在PO1点与PO3点之间。PN4点为PO1点水平延长线与PO2点垂线交点。PN3点为PO2点水平延长线与PO3点垂线交点。PN2点在PO2点垂线上,位于PO2点与PN4点之间。PN1点在PO2点水平线上,位于PO2点与PN3点之间。显然,PN1点与PN2点不在Pareto前沿,均为非Pareto最优解,而PN3点,PN4均非解。Pareto最优解在PO1,PO2,PO3点,相应IRDSMRD关键参数见表3。由于非Pareto最优解对应多组参数(L,N),表3只列出在PN1点、PN2点的非Pareto最优解结果,未列出参数组合。而PN3,PN4点为非解,故未给参数值。由表3、图5知,PO1点最优解表明通过优化参数可使IRDSMRD线性度优化为0.09%,而阻尼力降至99 N。PO3点最优解表明通过优化结构参数可使IRDSMRD阻尼力优化为804 N,而线性度恶化为11.3%。两解均为极端解,优化的以恶化为代价。 表3 Pareto最优解、结构参数及非Pareto最优解 实际上,关于阻尼力及IRDS线性度满意解可从Pareto前沿选取,如在PO1,PO3点之间。Pareto前沿上PO2点为IRDSMRD最优解,阻尼力为528.9 N,IRDS线性度为4.4%,与其对应的关键参数值见表3。而PN2,PN4点均不在Pareto前沿但具有与PO2相同的线性度却达不到PO2点阻尼力。即使PN4点的解能达到PO1点阻尼力,但PN4点IRDS线性度较PO1点线性度差的多。对不在Pareto前沿的点PN1,PN3,虽阻尼力与PO2点相同,却无PO2点IRDS线性度。PN3点IRDS线性度虽与PO3相同,但PN3点阻尼力却较PO3点差。因此可认为,在Pareto前沿的点均为最大阻尼力及IRDS线性度最优解,二者不可能同时提高,即一个目标优化必将削弱另一目标。 图5 N与L优化时所得最大阻尼力与线性度关系及Pareto最优边界 本文提出、研究并实现基于Pareto优化原理针对目标函数为IRDSMRD的阻尼力及IRDS线性度优化关键参数方法。对直接影响IRDSMRD阻尼力性能及IRDS传感性能的主磁通回路进行磁路建模与分析,并建立受磁动势与IRDSMRD结构参数影响的IRDS线性度数学模型、IRDSMRD阻尼力模型。结论如下: (1) 通过优化,当IRDSMRD体积一定时,可得IRDSMRD阻尼力性能与IRDS传感性能间关系的Pareto最优曲线(即Pareto前沿)。 (2) 不考虑IRDSMRD的IRDS线性度约束时,IRDSMRD阻尼力可为较大值(804 N),但此时IRDS传感性能较差(11.3%);而不考虑IRDSMRD阻尼力约束时,IRDS线性度会较好(0.09%),此时阻尼力亦较小(99 N)。 (3) 用本文关于IRDSMRD阻尼力及IRDS线性度均为最优的Pareto前沿,可实现对不同应用要求的IRDSMRD性能进行活塞头高度与励磁线圈匝数的协调设计。Pareto前沿对IRDSMRD设计具有一定指导意义。基于Pareto优化原理实现IRDSMRD两种性能间协调优化方法表明,该方法在基于智能材料自传感执行器的优化中存在普遍性。 [1]Wang D H,Liao W H.Semiactive controllers for magnetorheological fluid dampers[J].Journal of Intelligent Material Systems and Structures, 2005, 16(11/12):983-993. [2]Wang D H,Wang T.Principle, design and modeling of an integrated relative displacement self-sensing magnetorheological damper based on electromagnetic induction[J].Smart Materials and Structures,2009,18(9): 095025-095044. [3]Wang D H, Bai X X,Liao W H, An integrated relative displacement self-sensing magnetorheological damper: prototyping and testing[J].Smart Materials and Structures, 2010, 19(10): 105008-105026. [4]Wang Dai-hua,Bai Xian-xu.Pareto optimization based tradeoff between the damping force and the sensed relative displacement of a self-sensing magnetorheological damper[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(13): 1451-1467. [5]Rosenfeld N C,Wereley N M.Volume-constrained optimization of magnetorheological and electrorheological valves and dampers[J].Smart Materials and Structures, 2004, 13(6): 1303-1313. [6]Nguyen Q H,Choi S B.Optimal design of a vehicle magnetorheological damper considering the damping force and dynamic range[J].Smart Materials and Structures, 2009, 18(1): 015013-015022. [7]韩民春.西方经济学 (第二部分: 微观经济学) [M].北京: 北京大学出版社, 2007:273-280. [8]Papila M, Sheplak M,Cattafesta III L N.Optimization of clamped circular piezoelectric composite actuators[J].Sensors and Actuators A: Physical, 2008, 147(1):310-323. [9]Papila M, Haftka R T, Nishida T, et al. Piezoresistive microphone design pareto optimization: tradeoff between sensitivity and noise floor[J].Journal of Microelectromechanical Systems, 2006, 15(6): 1632-1643. [10]关新春, 郭鹏飞, 欧进萍.磁流变阻尼器的多目标优化设计与分析[J].工程力学, 2009, 26(9): 30-35. GUAN Xin-chun, GUO Peng-fei, OU Jin-ping.Multi-objective optimization of magnetorheological fluid dampers[J]. Engineering Mechanics, 2009, 26(9):30-35. [11]Wang D H, Wang T, Bai X X, et al. A self-sensing magnetorheological shock absorber for motorcycles[C]. Proceedings of 19thInternational Conference on Adaptive Structures and Technologies, Ascona, Switzerland, 2008. [12]Ashour O, Rogers C A,Kordonsky W I.Magnetorheological fluids: materials, characterization, and devices[J].Journal of Intelligent Material Systems and Structures,1996,7(2):123-130.2.3 表达式
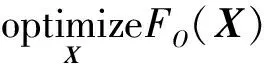
2.4 Pareto优化
3 结果与讨论
4 结 论
