磁流变阻尼器的改进多项式模型及验证
2014-09-05周铁明陈恩伟陆益民刘正士陈无畏
周铁明, 陈恩伟, 陆益民, 刘正士, 陈无畏
(合肥工业大学 机械与汽车工程学院,合肥 230009)
磁流变阻尼器(Magnetorheological Damper, MRD)以其结构简单,阻尼力连续可调,响应快,出力大,可靠性高且能耗低等优良性能,成为新一代高效的半主动控制的实现载体,广泛应用车辆(含汽车、高速列车)、卫星隔振平台、大型斜拉桥等的半主动振动控制[1-4]。为了设计控制策略和评价MRD在振动控制中应用的可行性,需要建立MRD的力学模型。由于MRD存在着一种特殊的力学性能-滞回特性,使其力学模型十分复杂,给建立精确的阻尼力模型和参数识别带来困难。
应用流变学理论分析流变后的MRD的力学特性非常复杂和困难,因此,通常采用MRD力学性能试验的结果来建立其数学模型。基于磁流变液屈服前和屈服后都是塑性且屈服前的阻尼远大于屈服后的阻尼的假设,Stanway[5]提出了非线性双粘性模型。该模型可较好地拟合阻尼力-位移滞回特性和阻尼器在每个振动周期内的能量耗散情况,但不能精确地拟合屈服前的阻尼力-速度滞回特性。Li等[6]对非线性双粘性模型进行拓展,提出了非线性滞回双粘性模型。该模型可以更好地模拟屈服前的阻尼器滞回特性,但不能拟合试验中MRD在低速时的回复力衰减现象。Spencer等[7-8]提出了Bouc-Wen模型,该模型数字上易于处理,能较好地反映阻尼器在低速时的滞回情况,但模型复杂,参数较多,不易辨识。Choi等[9]用多项式拟合阻尼力-速度曲线,令阻尼力为以活塞速度为自变量的一元高次多项式,强行使多项式系数与激励电流为线性关系。
本文在MRD力学性能试验的基础上,提出改进的多项式模型-分段3次多项式模型。该模型将阻尼力-速度曲线分为正加速度曲线(右支)和负加速度曲线(左支),采用文献[6]的分段方法将每支曲线分成3段,每段曲线用多项式进行拟合,且每个多项式的系数与激励电流不再为线性关系。
1 磁流变阻尼器的力学性能试验
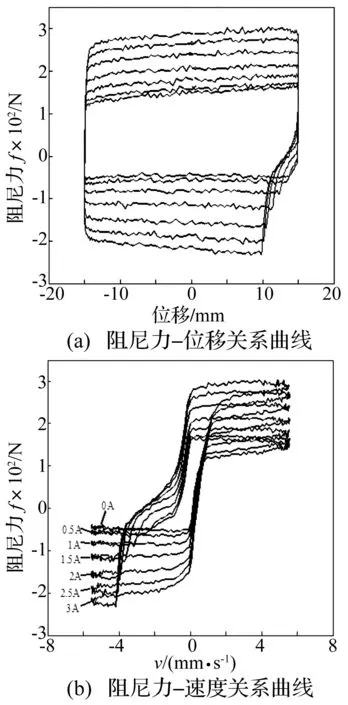
图1 磁流变阻尼器力学性能试验曲线
2 磁流变阻尼器建模
选择激励幅值为15 mm,频率为1 Hz,控制电流强度为0 A、0.5 A、1 A、1.5 A、2 A、2.5 A和3 A工况下的试验数据,采用基函数为多项式的最小二乘法进行MRD的动力学模型建立及参数识别研究。
2.1 多项式模型
文献[9]认为6次或更高次多项式就可以完全反映阻尼力-速度曲线的滞回特性,但彼此区别不大。在实际应用过程中发现,6次多项式和9次多项式的拟合精度差别较大,9次多项式的拟合精度比6次高;但9仍没达到精度要求。虽然多项式的阶数越高,拟合效果越好,但这也将使得需要辨识的参数变得更多。经过测试,12次的拟合效果很好,已经满足精度要求。12次多项式模型的计算公式为:
(1)
ai=bi+ciIi=0,1,…,12
(2)
激励幅值15 mm、激励频率1 Hz、控制电流1 A工况下9次,12次多项式拟合效果如图2所示。
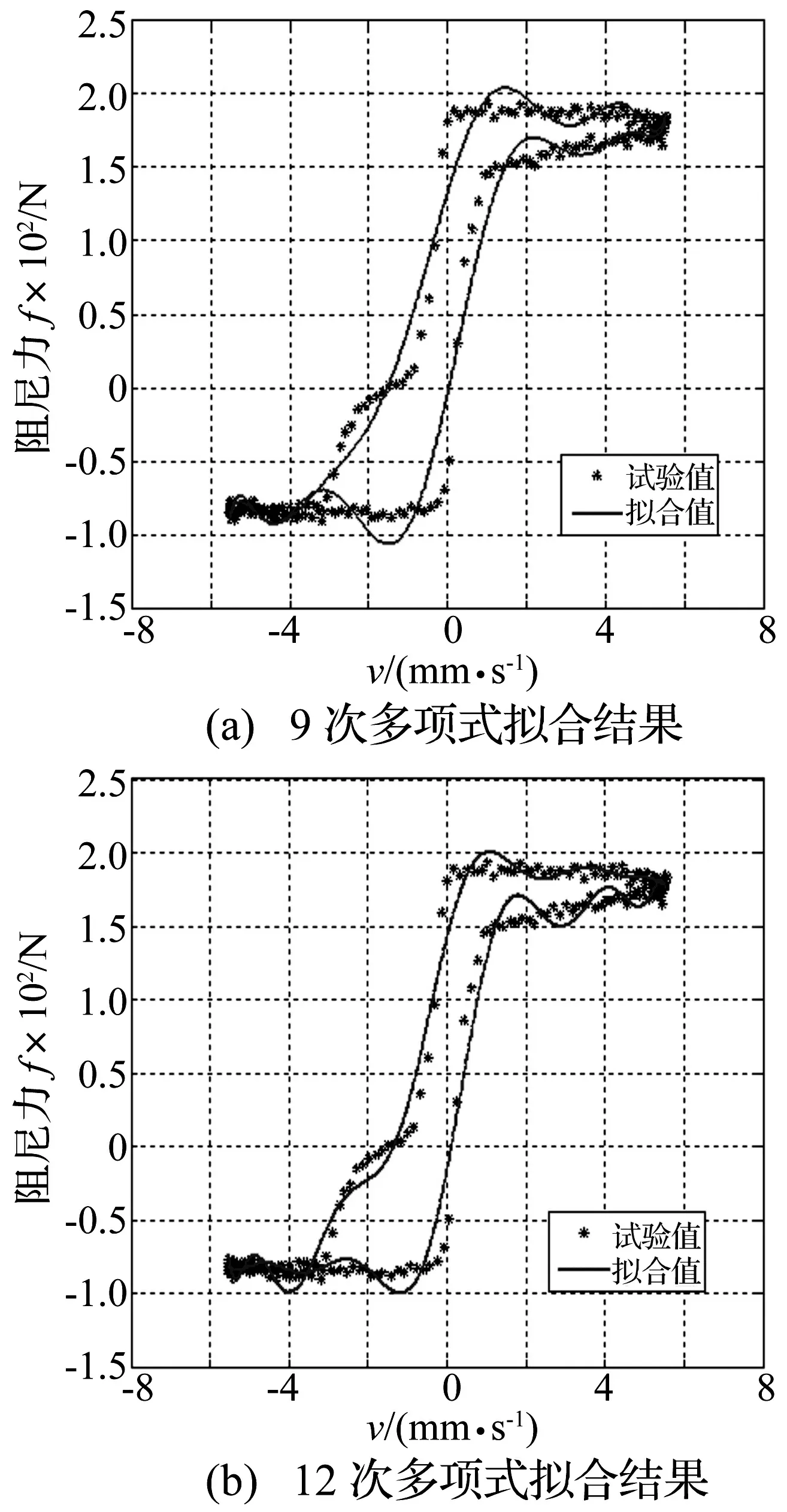
图2 各阶多项式拟合效果对比图
虽然12次多项式在高速区的拟合效果与实测结果有些偏差,但误差仍在可接受范围之内,因此采用12次多项式进行拟合。用最小二乘法[11]可以很容易地辨识出各电流情况下的ai,如式(3)所示。
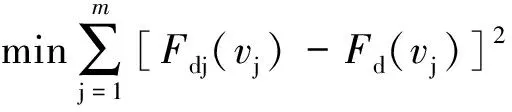
(3)
式中,ai为待辨识多项式系数;m为参与辨识的实测数据点数,m=12;vj为参与辨识的MRD活塞速度值;Fdj(vj)为参与辨识的实测阻尼力值,与vj一一对应;Fd(vj)为vj对应的12次多项式模型计算阻尼力值。
12次多项式强行使ai与电流I为线性关系,所以能够用直线拟合法辨识出截距bi和斜率ci值。当速度的绝对值较大时,多项式曲线的两端出现了剧烈的振荡,这就是龙格现象(Runge’s Phenomenon),如图3所示。造成这种现象的原因有:
(1) 速度绝对值较大处,采样点较多,相邻两个采样点之间,该多项式不一定能很好地逼近理想函数,产生很大的误差。
(2) 高次多项式由于计算量大,舍入误差的不断积累,使得多项式两端发散,造成拟合结果不合理。
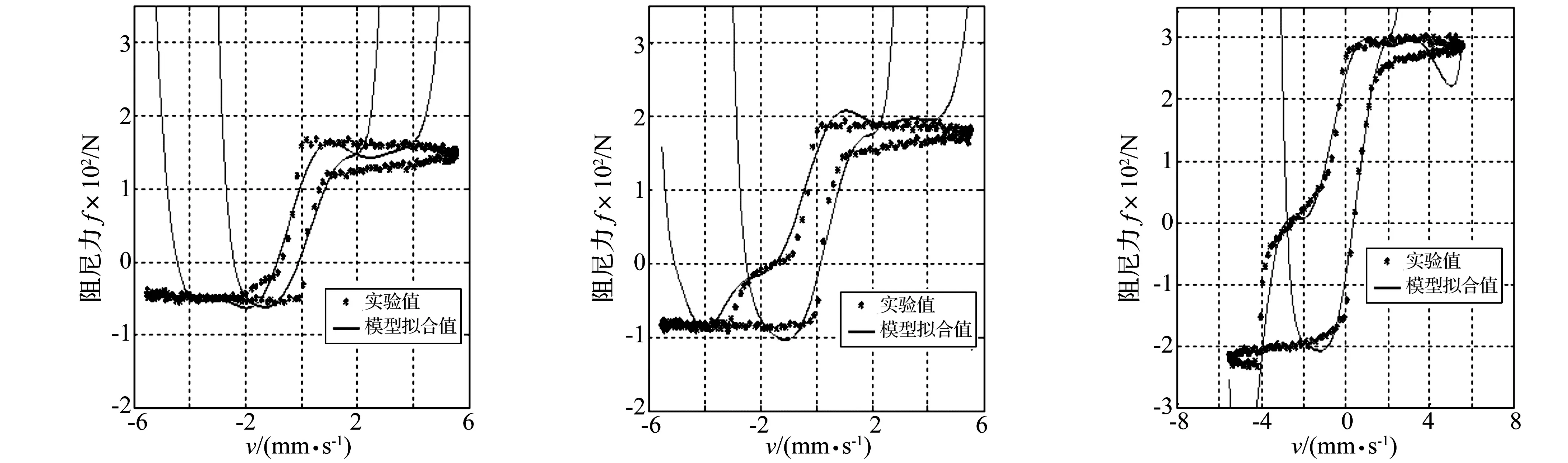
(a) 15mm、1Hz、0A时 (b) 15mm、1Hz、1A时 (c) 15mm、1Hz、3A时
2.2 分段3次多项式模型
Runge现象的出现,证明了高次多项式拟合具有较大的风险,因此在使用多项式模型时应尽量降低多项式的次数。为了解决Runge现象,可采用分段低次多项式对曲线进行拟合。借鉴文献[6]提出的非线性滞回双粘性模型的分段思想,预先确定的4个屈服速度,将正、负加速度曲线各分成3段,以屈服前后的速度点作为分段点,对每段曲线用多项式进行拟合,如式(4)所示。研究发现,虽然需要预先确定4个屈服速度,增加难度,但是计算所需多项式次数大大降低,能较好地克服了Runge现象:原来一整支曲线需用12次多项式拟合才能获得不错的效果,现在每段曲线只需用3次多项式拟合即可,而且拟合精度也得到提高。拟合结果如图4所示。
(4)
式中,ad1、ad2、ad3、au1、au2、au3为各分段多项式系数;
v1、v3为实际阻尼力-速度曲线减速时的屈服速度,为该分支曲线两个转折处的速度值;v2、v4为正加速时的屈服速度,也是该分支曲线两个转折处的速度值。v1、v2、v3、v4均是电流I的函数;

图4 分段3次多项式模型拟合效果
对比图2和图4,分段3次多项式的拟合精度比12次多项式的拟合精度高。为防止分段3次多项式模型的进一步复杂化,各分段多项式系数与电流之间用线性关系拟合,即a=b+cI。
分段多项式模型虽然提高了拟合精度并且能够防止Runge现象出现,但也存在一个明显的问题,即分段模型不是光滑连续,在每两段曲线的连接处可能出现不连续现象。为了使连接处尽量光滑过渡,在对每个分段计算时,分别向前和向后多取0.1N(N为该段点数)个采样点,最后该段共有1.2N个采样点参加计算。这样可以避免各分段的连接处出现不连续[11]。
采用最小二乘法对分段3次多项式模型进行参数辨识,结果如表1所示。
表中参数依据规则“下标d表示右支曲线,u表示左支曲线;下标中第1个数值1、2、3分别表示第1、2、3段曲线;下标中第2个数值0、1、2、3分别表示多项式的
常数项、一次项、二次项、三次项系数的拟合值”类推。如“,bd10、cd10表示右支曲线第一段多项式中常数项ad10的拟合参数值,即ad10=bd10+cd10I”。
屈服速度v1、v2、v3、v4与电流的关系如图5所示。
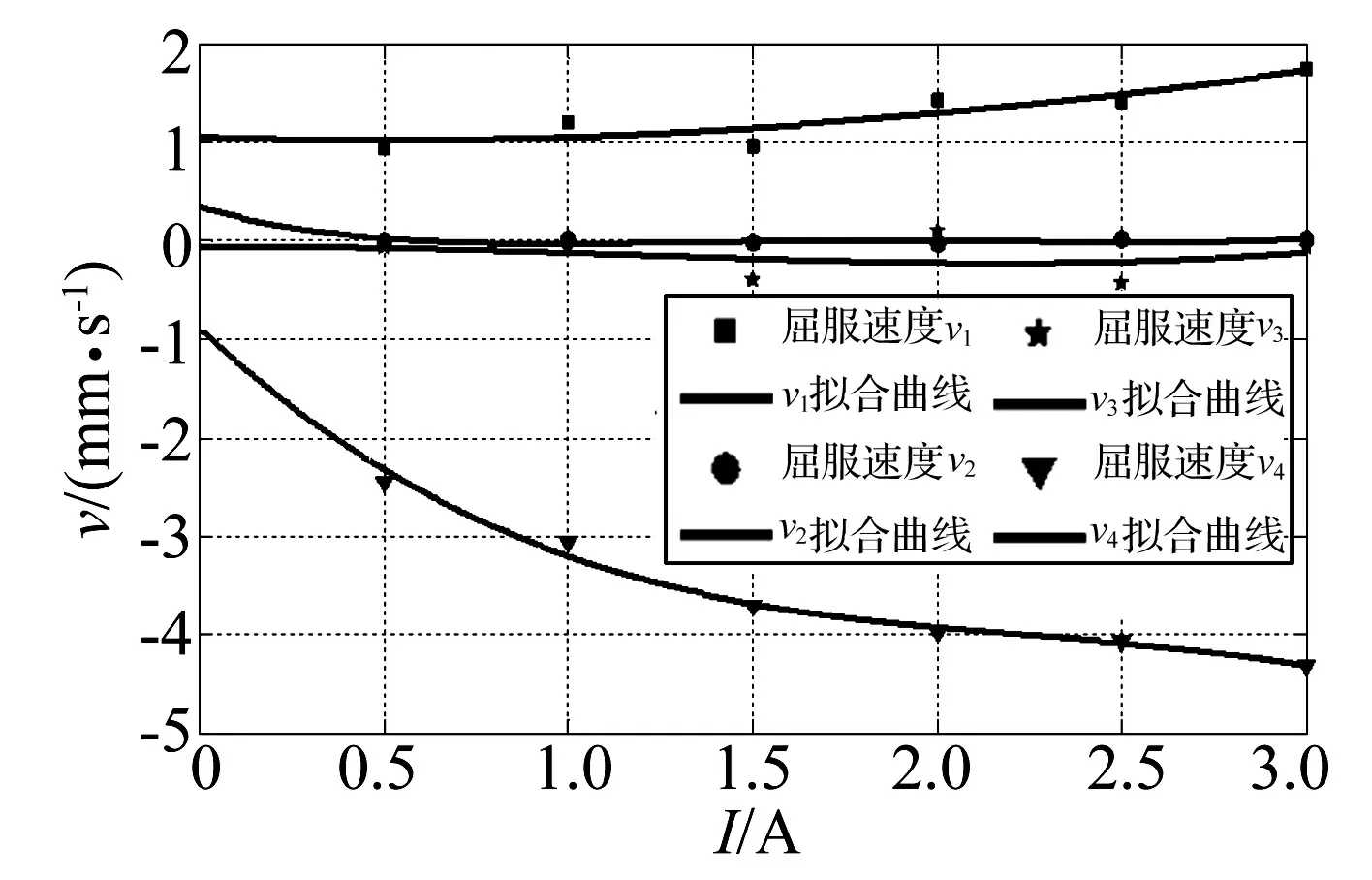
图5 屈服速度与电流I的关系
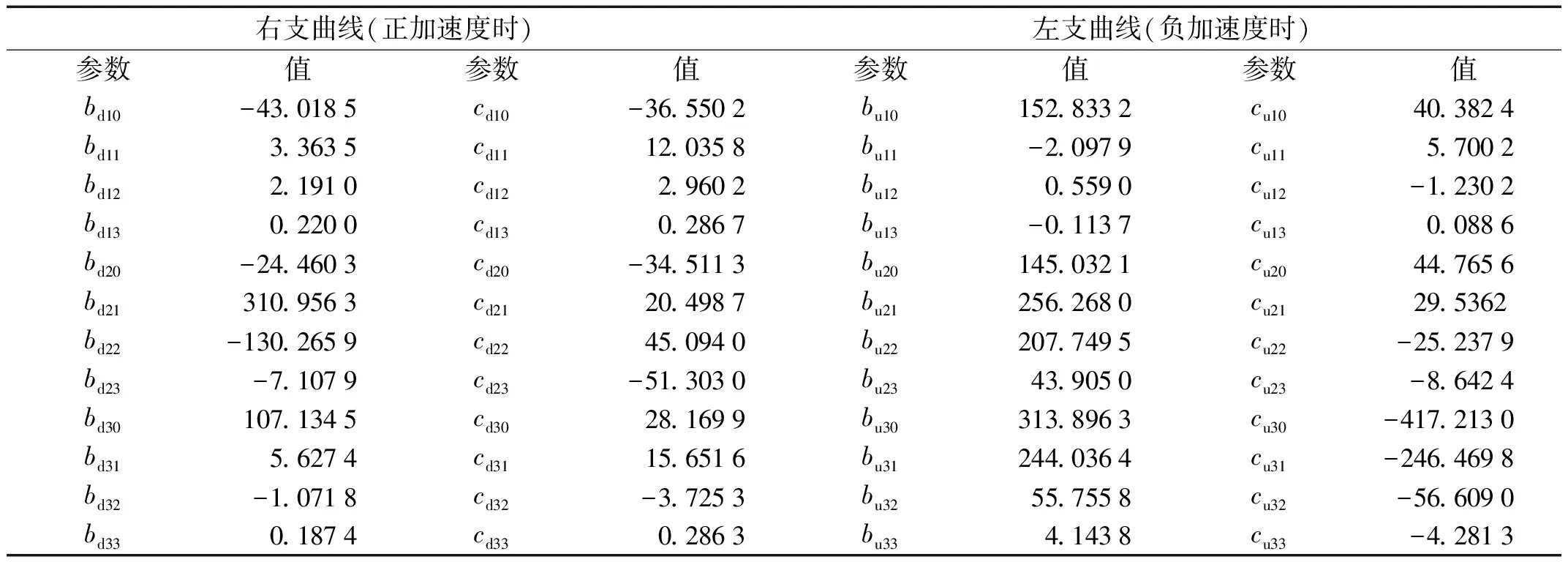
表1 分段3次多项式模型参数表
经过多项式拟合,得到各屈服速度与电流的关系,如式(5)~式(8)所示。不同型号的磁流变阻尼器的结构、尺寸以及内部线圈的扎数不尽相同,所以4个屈服速度与电流的关系是针对一定型号磁流变阻尼器而确定的系数。磁流变阻尼器的型号改变,系数也会随之改变。
v1=-0.007 248I3+0.141 633I2-0.136 455I+1.059 053
(5)
v2=0.057 119I4-0.410 437I3+1.030 562I2-1.044 846I+0.339 158
(6)
v3=0.043 268I3-0.153 423I2+0.053 011I-0.069 076
(7)
v4=-0.207 829I3+1.417 490I2-3.524 325I-0.888 611
(8)
3 模型验证及误差分析
3.1 模型验证
利用参数辨识结果,计算未参与模型辨识的3种工况下模型的预测阻尼力,并与实测阻尼力值进行比较,结果如图6所示。
从图中可看出,分段3次多项式模型的计算阻尼力和实测阻尼力值基本重合,Runge现象消失,说明该模型能够较好地描述MRD的阻尼力-速度之间的非线性特性和滞回特性。
3.2 误差分析
由于平均误差是对每一段上不同点的平均,并不能反映每一点的情况,按照误差分析常用的相对误差分析方法,本小节通过分析在幅值为15 mm,频率为1 Hz激励下,各对应速度下模型计算阻尼力值与实测阻尼力之间的相对误差,进一步评价分段3次多项式模型的有效性。
模型的相对误差由式(9)表示:
(9)
式中,Fd(vj)表示vj速度下分段3次多项式模型的计算阻尼力值;
Fdj(vj)表示vj速度下实测阻尼力值。
选取0.5 A、1.5 A、2.5 A电流下的数据进行误差分析,分别代表小电流、中电流、大电流三种情况,计算结果如图7所示。

(a) 15mm、1Hz、0.5A时 (b) 15mm、1Hz、1.5A时 (c) 15mm、1Hz、2A时

(a) 15mm、1Hz、0.5A时 (b) 15mm、1Hz、1.5A时 (c) 15mm、1Hz、2.5A时
eu1、eu2、eu3分别表示左支曲线第1段、第2段、第3段的模型计算阻尼力值与实测值的相对误差。从图7可看出,3种电流情况下,分段3次多项式模型均是第1段和第3段时误差较小,第2段时误差最大,也即模型在滞环速度区(低速区)的误差最大;即使同在第2段,左支曲线的误差比右支曲线的误差大得多。这是因为在第2段的采样点数少于第1段和第3段,造成第2段多项式的拟合误差大于第1段和第3段,经过参数辨识,误差积累放大,再利用模型计算阻尼力时,第2段的误差自然比第1段和第3段大。由于模型计算出的穿越速度滞后于实际的穿越速度,导致在计算穿越速度与实际穿越速度之间,模型的计算阻尼力值与实测值符号相反,式(9)中的分子非但没有减小,反而增大,变得比分母还大,最终的误差计算值超过了100%,这就是第2段上支曲线的最大误差分别为110.6%、369.1%、397.8%的原因。虽然误差超过了100%,但在穿越速度附近,阻尼力的值比较小,这么大误差产生的实际影响并不大。
随着电流的增大,第1段和第3段及右支曲线第2段的误差逐渐减小,验证了多项式系数对于电流影响的敏感性。从整体来看,分段3次多项式模型具有较高的精度,能够较准确地反映MRD的阻尼力-速度关系。
4 结 论
(1) 6次多项式或更高次多项式都可以反映阻尼力-速度曲线的滞回特性,但区别较大。多项式的阶数越高,阻尼力-速度曲线的拟合效果越好,但高次多项式拟合易出现Runge现象,导致拟合曲线的两端出现剧烈地振荡。
(2) 经过验证,分段3次多项式模型能够有效地消除Runge现象,且拟合精度较高。因此,分段3次多项式模型能够较好地描述MRD阻尼力-速度曲线的非线性特性和滞回特性。
参 考 文 献
[1]刘永强, 杨绍普, 申永军.基于磁流变阻尼器的汽车悬架半主动相对控制[J].振动与冲击, 2008, 27(2):154-156.
LIU Rong-qiang, YANG Shao-pu, SHENYong-jun. Semi-active relative control schemes forvehicle suspension using amagnetorheologicaldamper[J]. Journal of Vibration and Shock, 2008,27(2):154-156.
[2]陆正刚, 胡用生.基于磁流变阻尼器的铁道车辆结构振动半主动控制[J].机械工程学报,2006,42(8):95-100.
LU Zheng-gang, HU Yong-sheng. Semi-active control of railway vehicle structural vibrationbased on MR damper[J]. Chinese Journal of Mechanical Engineering, 2006, 42(8):95-100.
[3]涂奉臣, 陈照波, 刘望中,等.新型半主动整星隔振平台及其模糊最优控制研究[J].振动工程学报, 2010, 23(2):133-139.
TU Feng-chen, CHEN Zhao-bo, LIU Wang-zhong, et al. A new type semi-active whole-spacecraft isolation platform and its fuzzy optimal control[J]. Journal of Vibration Engineering, 2010, 23(2):133-139.
[4]Ok S Y, Kim D S, Park K S, et al.Semi-active fuzzy control of cable-stayed bridges using magneto-rheologicaldampers[J].Engineering Structures, 2007, 29:776-778.
[5]Stanway R, Sproston J L, EI-Wahed A K, Applications of electro-rheological fluids in vibaration control: a survey [J]. Smart Materials and Structures, 1996,5(4): 464-482.
[6]Pang L, Kamath G M, Wereley N M, Analysis and testing of a linear stroke magnetorheological damper[J]. AIAA 98-2040,1998, CP8903(4): 2841-2856.
[7]Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model of a magnetorheological damper [J]. Journal of Engineering Mechanics, ASCE, 1997,123(3):230-238.
[8]Dyke S J, Spencer B F, Sain M K, et al. Modeling and control of magnetorheological dampers for seismic response reduction [J]. Smart Materials and Structures, 1996, 5(5): 565-575.
[9]Choi S B, Lee S K, Park Y P, A hysteresis model for the field-dependent damping force of a magnetorheological damper [J]. Journal of Sound and Vibration, 2001, 245(2): 375-383.
[10]朱晓临, 数值分析[M]. 合肥: 中国科学技术大学出版社, 2010.
[11]陈恩伟,陆益民,刘正士,等. Taylor展开的线性时变系统参数辨识及误差分析[J]. 机械工程学报, 2011, 47(7): 90-96.
CHEN En-wei, LU Yi-min, LIU Zheng-shi, et al. Parameter identification and error analysis of linear time varying system based on Taylor expansion[J]. Journal of Mechanical Engineering, 2011, 47(7):90-96.
