汽车碰撞安全风险决策中基于复合聚类的群决策专家权重确定方法
2014-09-05王素娟雷正保
王素娟, 雷正保, 赵 建
(1. 长沙理工大学 道路灾变防治及交通安全教育部工程研究中心,长沙 410004;2.长沙理工大学 汽车与机械工程学院,长沙 410004;3.三一重工 湖南汽车制造有限责任公司研究院,长沙 410000)
在汽车碰撞安全研究中,风险决策决定着碰撞风险评估的准确性和系统对评估出的风险作出决策反应的正确性,对汽车碰撞安全系统的研究和发展具有重要意义。目前,风险决策研究已有成熟发展,但针对汽车碰撞安全的风险决策欠缺系统的研究方法,也鲜有将风险决策用于相关安全系统装置的研究。
基于以上论述,本研究将风险决策用于汽车碰撞安全系统,尤其是主被动结合的安全系统装置,在行车过程中,对可能引发汽车碰撞发生的多种风险因素进行评估,再将系统探测到的多种适时风险因素信号作为决策依据,使系统作出相应的控制决策(如发出警报信号、减速制动或控制相应的被动安全装置即时工作等),避免现有一些安全装置单纯依靠监测距离频繁自动制动情况的发生,也为汽车碰撞主被动结合安全系统的研究开发奠定基础[1-4]。
在汽车碰撞安全风险评估的过程中,需采用专家调查法获取相应的数据,该过程为一群决策过程。在群决策过程中,决策者们提供的多组专家意见的数据处理决定了分析结果的发展趋势和可靠性。其中,专家权重是合并专家数据的重要系数。因此,专家权重在群决策分析数据处理中占据重要地位。
本文研究的内容属于“基于风险评估的汽车碰撞安全决策方法及其应用”系统研究内容的一部分,主要研究在汽车碰撞安全风险决策中的群决策专家权重的确定方法。在现有的群决策分析数据处理的专家权重确定方法中,常用的有算术平均或几何平均法、根据专家的学术地位和水平及职称赋权法、频度统计法、灰色系统理论法、决策成员互评法、依据个体数据一致性和个体与群体距离的客观权重赋权法和基于数据一致性程度的聚类赋权法等[5-7]。以上方法通用性较好,但具体用于某一行业研究时,无法针对行业特色,可能会导致结果上的偏差。例如,假设决策者队伍中有一位驾驶经验十分丰富但职称和学术水平不高的司机和一位职称和学术水平较高的汽车排放研究专家,若按通用方法,排放研究专家将会被赋予较高权重,但就汽车碰撞安全而言,该司机应被赋予更高权重才更为合理。
本文针对汽车碰撞安全的行业特色,提出一种有专业针对性的专家权重确定方法,避免单纯依靠专家的社会地位或者单纯依靠专家提供的数据一致性造成不合理的赋权。
1 基于复合聚类的专家权重确定方法
基于复合聚类的专家权重确定方法分为三个步骤:首先依据专家的社会因素指标对专家进行权威权重聚类,并赋予各类权重;其次依据专家提供的数据从个体一致性以及个体与群体一致性出发对专家进行意见权重聚类;最后将以上两种分类的类权重各赋予一定的系数并取交集进行复合聚类,以确定各位专家的最终复合权重。
1.1 权威权重聚类分析
1.1.1 指标的选取及评判标准的制定
为获取信息的多样性和全面性,需要向多名专家进行数据调查。针对汽车碰撞安全研究对象,根据应用对象的特征,来明确什么是真正的专家。头衔高的不一定是专家,只有真正从事本专业工作的人才是专家,如司机、汽车爱好者和汽车维修人员,也许没有任何科研项目的研究经历,但由于长期从事并关注汽车方面的工作,其意见具备较高的参考价值。因此,专家权重要体现行业、专业特色。汽车安全专家、汽车安全管理人员、司机、汽车爱好者、汽车维修人员等应有较大权重;汽车业内人士,应有一般权重;非汽车业内人士,应有较小权重。
不同研究领域、学术地位、职称、职业等的专家,应被赋予不同权重。影响专家权重的社会因素指标有很多,指标的选取对于聚类结果的影响较为重要,综合以上专家的职业特点,本文采用十项指标作为专家权威权重聚类的影响因素指标:专业相关系数、接触或研究汽车时间、是否专职司机、驾龄、驾驶证类别、工作单位、工龄、学位、学术水平、职称。
由于以上十项指标兼顾了各种专家的职业特点,为达到一个较为均衡的评判标准,在评判标准分数上统一采用满分十分制,具体评判标准则依据各项指标的等级分层酌情分配[8],其中对于个体户的工龄则按照接触或研究汽车时间进行赋值,见表1-表10所示。

表1 专业相关系数

表2 接触或研究汽车时间

表3 是否专职司机

表4 驾龄

表5 驾驶证类别

表6 工作单位

表7 工龄

表8 学位

表9 学术水平

表10 职称
1.1.2 聚类方法的选择
为选择更为合理的聚类解,聚类方法采用K-均值聚类分析以及系统聚类法中应用较广的基于方差分析思想的离差平方和法(Ward’s Mehtod)相结合的方法。利用SPSS(Statistical Product and Service Solutions,统计产品与服务解决方案)软件,首先选择系统聚类方法进行计算,得出树状图,对树状图用切割法分为m、n和q类,再分别将m,n,q作为聚类个数,利用SPSS依据社会因素指标数据对专家进行K-均值聚类,将两种聚类方法的结果进行比较,同时对K-均值聚类各结果的平均数差异进行检验,进一步验证所选取聚类解的合理性。
1.1.3 专家权威权重的聚类分析
设对于调查的十五位专家的十项社会因素指标评判标准分值如表11所示。将表11中的数据输入SPSS的数据编辑器,首先用聚类分析(度量标准选用“平方Euclidean距离”,聚类方法选用“Ward法”)方法得出聚类树状图如图1所示,用切割法可以将专家聚为2、3、4和5类;再用K-均值聚类方法(聚类数依据图1分别选为2、3、4、5),得出聚类成员表如图2、图3、图4和图5所示。

图1 系统聚类树状图

表11 十五位专家的十项社会因素指标评判标准分值

图2 聚类数为2
依据图1-图5显示数据,采用系统聚类方法和K-均值聚类方法得到表12的多种聚类结果。针对这组专家权威指标的聚类,分为4类时,两种分类方法的聚类解相同。同时对K-均值聚类的4类聚类结果进行平均数差异的检验,检验结果如表13所示,除了个别指标,其他指标都达到了显著性的水平,证明聚为4类的分类结果是比较有效的。分析表12中聚为4类的结果:专家6、7是各项指标得分比较大的汽车安全专家和汽车安全管理人员;专家3、5、9、10、11、13、14、15均为专业相关系数为10的专职司机、汽车爱好者、汽车安全管理人员和汽车维修人员;专家2、12的专业相关系数虽然不同,但是专家2属于非安全领域的汽车业内人士中各项得分较高的,专家12属于汽车安全专家中各项得分较低的;专家1、4、8为非汽车业内人士和非安全领域的汽车业内人士。分析聚为3类和聚为5类的聚类结果,3类分法稍显粗略,5类分法过于细致并无必要。因此,依据两种聚类方法得出的综合结果,通过对K-均值聚类的聚类结果进行平均数差异的检验,以及分析专家各项指标得分和专家职业,得出的4类聚类结果较为合理。故,对十五位专家的聚类结果是4类:A1=[1,4,8],A2=[2,12], A3=[6,7],A4=[3,5,9,10,11,13,14,15]。
1.1.4 专家权威聚类权重计算
上述十项指标的选取综合考虑了各类职业专家的职业评分特点,其评判标准分值的制定也结合了与汽车安全研究有关的特点,以期可以对行业内较有经验的汽车安全专家、专职司机、汽车维修人员等,可以赋予较高权重,因为他们提供的行车安全意见是结合自身经验而来,准确性和参考价值较高。为了区分出各类专家之间的权重,取每位专家的指标总分为专业相关系数与其他九项指标得分总和的乘积。
假设专家聚类结果将m位专家分为n类,则第k位专家的指标总分为
Fk=Z1k×(Z2k+Z3k+…+Z10k)
(k=1,2,…,m)
(1)
设第t类中有q位专家,则第t类专家的聚类平均分为
(2)
那么第t类的专家权威聚类权重为
(3)
将表11中的数据代入式(1)(2)(3)得出
WA1[1,4,8]=0.1,WA2[2,12]=0.21
WA3[3,5,9,10,11,13,14,15]=0.31,WA4[6,7]=0.38
由以上聚类权重计算结果可以看出,各项指标分值居高的汽车安全专家6和汽车安全管理人员7得到最高权重0.38;专职司机3、9和14,汽车爱好者5和10,汽车安全管理人员11,汽车维修人员13和15得到较高权重0.31;非安全领域的汽车业内人士2和各项分值较低的的汽车安全专家12得到较低权重0.21,;非汽车业内人士1和8,非安全领域的汽车业内人士4得到最小权重0.1。
由聚类结果和权威权重计算结果可以看出,对汽车安全研究较为深入的汽车安全专家、汽车安全管理人员得到最高权重,对汽车安全有较深体会和实践经验的专职司机、汽车爱好者和汽车维修人员得到较高权重,非安全领域的汽车业内人士和非汽车业内人士得到较低权重。在兼顾所有专家意见的前提下,针对汽车安全研究的行业特色,使得专职司机、汽车爱好者和汽车维修人员等这些有着丰富实践经验的专家得到了较高权重,避免了传统的仅仅依靠学位职称等社会指标给专家赋权而造成的与实际偏离结果的出现,权重计算结果有较为明显的区分。由此可以证明,上述十项指标的选取、评判标准及其分值的制定、聚类方法和聚类结果的选择、聚类权重的计算是有效合理的。
1.2 专家意见权重聚类分析
该系统研究的风险评估采用层次分析法进行,本文的意见权重聚类分析的专家意见依据各位专家提供的判断矩阵进行。本文依据周漩等在文献[9]提出的基于信息熵的方法,运用熵原理对专家们进行聚类,具体方法参见文献[9],在此不再赘述。
需要说明的是,文献[9]在对专家进行聚类后,在计算每位专家权重时运用了专家人数这一概念,当某一专家单独成一类时,该专家的类内权重被赋值为1,等于赋给了一个意见不太合群的专家一个较高的类内权重,会拉高该专家的最终权重,这种处理方法并不合理。所以,本文利用文献[9]的方法计算专家意见聚类类间权重,不再计算每位专家的权重。得到各类专家意见聚类权重结果如下:
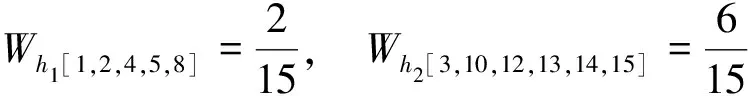
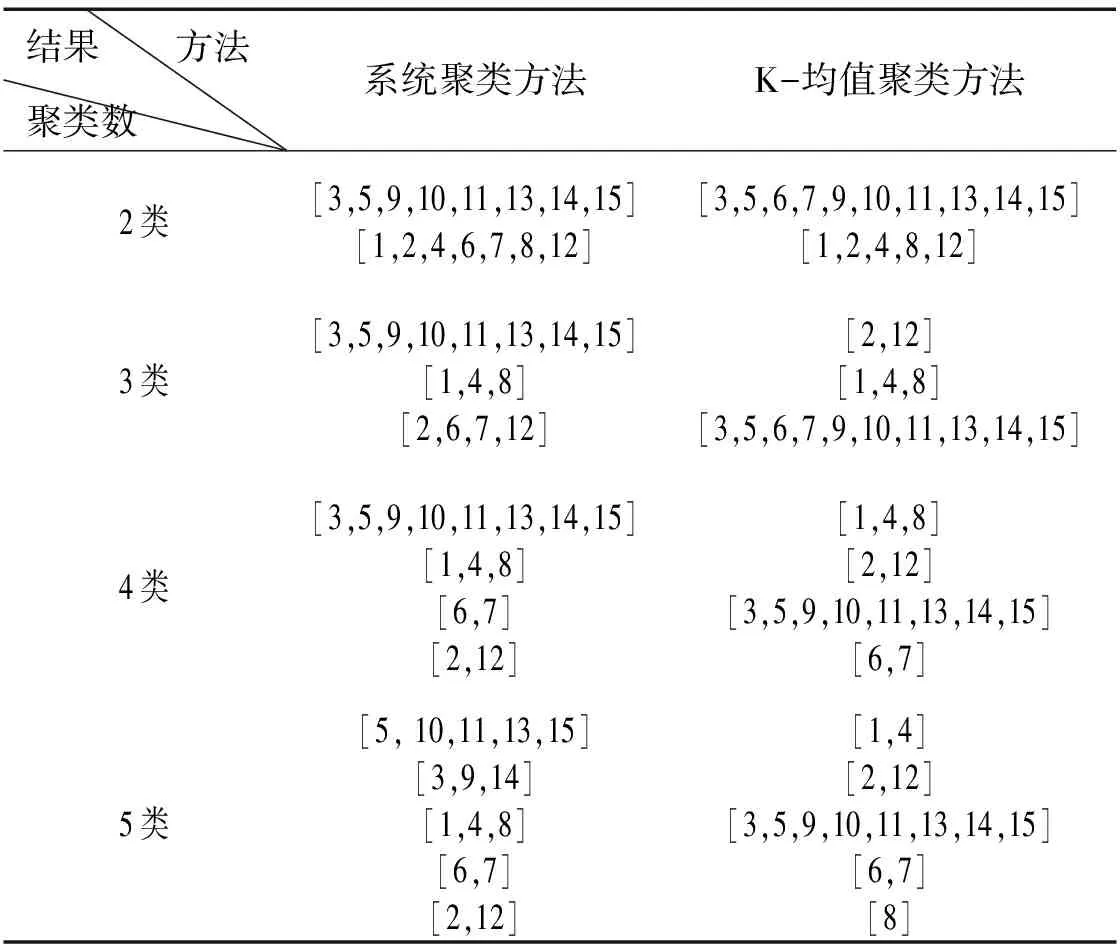
表12 聚类结果
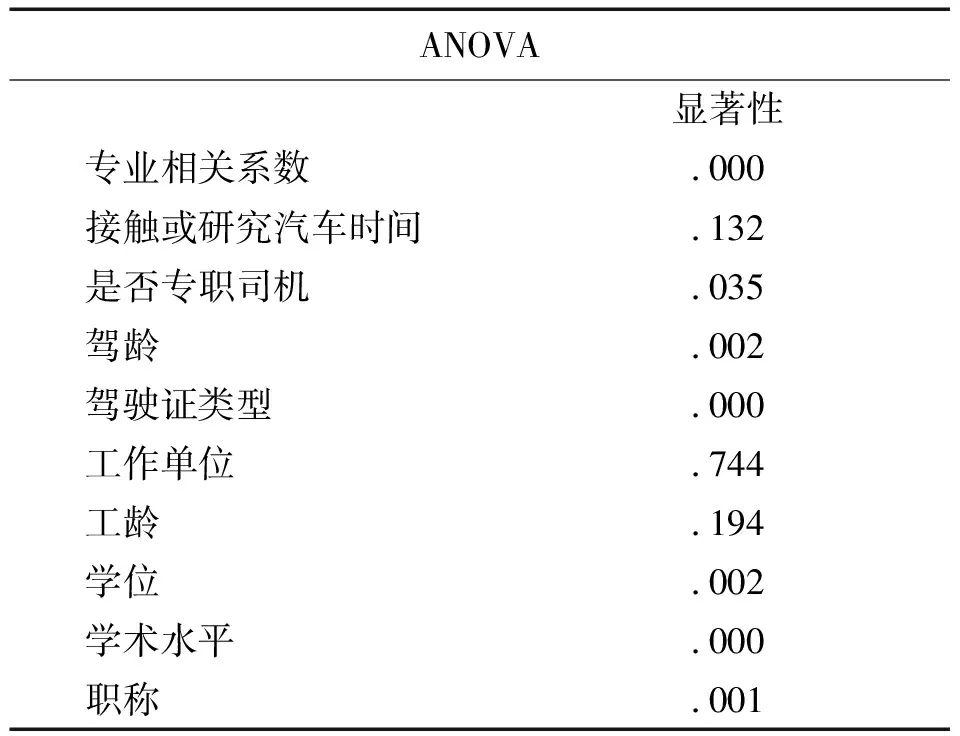
表13 聚类数为4的检验结果
1.3 复合聚类的专家权重分析
1.3.1 复合聚类方法
将上述专家权威权重聚类和专家意见权重聚类的结果进行复合,求交集,得到复合后新的分类。假设专家权威聚类分为m类,其中第x类表示为Ux,其类权重为WAx(x=1,2,…,m),专家意见聚类分为n类,其中第y类表示为Vy,其类权重为Why(y=1,2,…,n)。求各个Ux与各个Vy的交集,得到一组交集数据,即为复合后的新的专家聚类。设共得到交集数为c,SAxhy为Ux与Vy的交集,交集内专家数为r,记SAxhy的复合聚类类指数为Qi=r[αWAx+βWhy],(i=1,2,…,c)(其中,α+β=1,r为该类中专家总人数)。在此,由于专家意见相对专家权威略重要,故α取0.4,β取0.6,其他情况可酌情取值。则各复合聚类的专家权重为
(4)
聚类内专家较多的类,因为乘以了类内专家总人数r,故可得到较高权重。基于上述方法,经过复合聚类后同一类的专家拥有相近的社会权威地位和相近的数据一致性,因此复合聚类后的同类专家基本具有同等个人权重,可以在此基础上进行后续的数据处理。
1.3.2 算例分析
将上述两种聚类结果
WA1[1,4,8]=0.1,WA2[2,12]=0.21
WA3[3,5,9,10,11,13,14,15]=0.31,WA4[6,7]=0.38
和
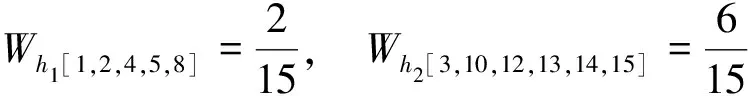
进行复合,由式(4)可得复合聚类后的各类权重为:
W1[3,10,13,14,15]=0.4,W2[6,7]=0.19
W3[9,11]=0.18,W4[1,4,8]=0.08
W5[12]=0.07,W6[5]=0.044
W7[2]=0.036
依据复合聚类的权重计算结果,个体意见与群体意见一致性较高的专职司机3、14,汽车爱好者10,汽车维修人员13、15获得了最高权重,个体意见与群体意见一致性较低非安全领域的汽车业内专业人士2获得了最低权重,该结果综合了专家权威权重与专家意见权重,合理有效。
2 应 用
本文的复合聚类主要用于“基于风险评估的汽车碰撞安全决策方法及其应用”中的几个系统分析中的数据处理,用来在专家对减少碰撞事故的各因素影响大小和对汽车碰撞安全系统各种装置起作用的大小提供数据时,对专家权重进行分析,为后续数据处理提供基础。
3 结 论
本文针对汽车安全研究的行业特色,依据专家社会因素指标对专家进行权威权重聚类,依据专家提供意见的一致性程度以及个体与群体一致性程度对专家进行意见权重聚类,进而将这两种聚类结果进行复合聚类,得到专家的最终权重。本文研究内容属于“基于风险评估的汽车碰撞安全决策方法及其应用”系统研究的一部分,使数据处理的结果具有较好的均衡性和可靠性。
感谢长沙理工大学道路灾变防治及交通安全教育部工程研究中心开放基金和国家自然科学基金的资助。
参 考 文 献
[1]雷正保,王素娟,付爱军,等.汽车碰撞的安全与吸能[M].长沙:国防科技大学出版社,2008.
[2]王素娟,雷正保,赵建. 带保险杠系统的螺纹剪切式汽车碰撞吸能装置的电子控制系统[J].振动与冲击,2009,28(2):181-186.
WANG Su-juan, LEI Zheng-bao, ZHAO Jian. Electronic control system of energy-absorbing equipment of screw shear type and attached with bumper system for mitigation of automobile collision[J]. Journal of Vibration and Shock, 2009,28(2):181-186.
[3]杜青云,雷正保,魏书彬. 汽车碰撞预警与碰撞吸能技术结合的CST控制系统[J].中国机械工程,2011.22(6):751-755.
DU Qing-yun, LEI Zheng-bao, WEI Shu-bin. CST control system based on combination of automotive collision warning and collision energy absorption technology[J]. China Mechanical Engineering, 2011,22(6):751-755.
[4]WANG Su-juan, LEI Zheng-bao, LI Yong-han, et al. A research of real-time protective barrier system for automobile safety[C], 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Volume 1 (Paper number:E45790), 58-61,April 16-18, 2011,XianNing, China, IEEE Catalog Number: CFP1153N-PRT,ISBN: 978-1-61284-470-1.
[5]高阳,罗贤新,胡颖.基于判断矩阵的专家聚类赋权研究[J].系统工程与电子技术,2009,31(3):593-596.
GAO Yang, LUO Xian-xin, HU Ying. Research on methods for deriving experts’ weights based on judgment matrix and cluster analysis[J]. Systems Engineering and Electronics, 2009,31(3):593-596.
[6]周延年,朱怡安.基于灰色系统理论的多属性群决策专家权重的调整算法[J].控制与决策,2012,27(7):1113-1116.
ZHOU Yan-nian, ZHU Yi-an. Algorithm for adjusting weights of decision-makers in multi-attribute group decision-making based on grey system theory[J]. Control and Decision, 2012,27(7):1113-1116.
[7]陈晓红,刘益凡.基于区间数群决策矩阵的专家权重确定方法及其算法实现[J].系统工程与电子技术,2010,32(10):2128-2131.
CHEN Xiao-hong, LIU Yi-fan. Expert weights determination method and realization algorithm based on interval numbers group decision matrices[J]. Systems Engineering and Electronics, 2010,32(10):2128-2131.
[8]冯中朝,李强.科研项目评估中专家权重确定的方法与模型[J].科技管理研究,2000(4):47-50.
FENG Zhong-chao, LI Qiang. Method and model to determine expert weights in the project assessment[J]. Science and Technology Management Research, 2000(4):47-50.
[9]周漩,张凤鸣,惠晓滨,等.基于信息熵的专家聚类赋权方法[J].控制与决策,2011,26(1):153-156.
ZHOU Xuan, ZHANG Feng-ming, HUI Xiao-bin, et al. Method for determining experts’weights based on entropy and cluster analysis[J]. Control and Decision, 2011,26(1):153-156.
