机动飞行时直升机尾传动轴的横向振动建模与特性

倪 德， 朱如鹏， 靳广虎， 李发家

(南京航空航天大学 江苏省精密与微细制造技术重点实验室， 南京 210016)

由于直升机常常做非匀速的空间机动飞行运动，直升机的传动轴工作在一个非惯性系下，其动力学特性与惯性坐标系下的传动轴会有很大的区别。飞机的机动飞行会在转子系统上作用附加载荷，影响转子的正常工作[1,2]。直升机尾传动轴系构成直升机最长的传动链，负责向尾旋翼传递动力，其工作状态直接影响直升机的性能。直升机机动飞行引起的附加载荷，更容易造成传动轴的破坏。因此，有必要研究机动飞行下直升机尾传动轴的动力学特性。

林富生等[3-5]研究了飞机在水平或垂直平面作等加速和变加速运动时单盘转子系统的动力学特性。徐敏等[6-7]研究了水平盘旋和俯冲拉起两种机动飞行条件对双盘悬臂转子振动特性的影响。后来他们又研究了机动飞行条件下带挤压油膜阻尼器的Jeffcott 转子的振动特性。顾致平等[8]研究了飞机水平盘旋下处于一定角速度的刚性和弹性不同支承情况下转子的瞬态响应。惠旭升等[9]从非惯性参考系中质点的运动微分方程出发，推导出转子考虑非惯性力及陀螺力矩影响条件下的盘心运动分量方程函数。祝长生等[10-11]建立了飞机在任意空间机动飞行时发动机安装在飞机上任意位置条件下不平衡多盘、多质量和多轴承线性及非线性柔性转子系统动力学的统一模型，讨论了飞机的空间机动飞行对发动机转子系统动力特性的影响。张群岩等[12]在祝长生等人研究工作的基础上，利用某型发动机的试飞数据对机动飞行条件下发动机转子振动特性的一般性进行了验证和分析。杨永锋等[13-14]研究了裂纹转子在俯冲拉起和水平盘旋机动飞行条件下的动力学特性。

直升机尾传动轴采用细长的空心轴，具有质量连续分布的特点。以上研究工作主要针对单盘或转子系统，采用集中质量模型，所以不适应于尾传动轴的研究。许兆棠[15]考虑了非惯性系对直升机尾传动轴的影响，但仅考虑了水平和垂直方向加速度的影响。本文的主要工作是建立直升机空间机动飞行时尾传动轴的动力学模型，分析机动飞行对传动轴的影响，为直升机传动轴系的计算分析与工程实践提供参考。

1 机动飞行下尾传动轴的动力学方程

1.1 坐标系和运动描述

将直升机机体当作一个刚体，在空间有六个自由度，则可以利用刚体的位姿描述方法，即将直升机的运动分解为随基点的平动与绕自身重心的转动，来描述直升机机动飞行时的空间位姿，如图1所示。选取地球为惯性系，O0为此惯性空间中的一定点，过该点建立固定坐标系O0x0y0z0，用于描述直升机的平动特性，主要为直升机的飞行速度和飞行加速度。以直升机的重心为原点且固连在直升机机体上的相对坐标系ORxRyRzR，用于描述直升机的转动特性。其中，ORzR轴为机身对称轴，指向与直升机飞行方向相反。于是，直升机的空间位姿可由固定坐标系O0x0y0z0上的平动分量[X0，Y0，-Z0]T和相对坐标系ORxRyRzR上的转动分量[θxR，θyR，-θzR]T来描述。其中，绕ORxR轴和ORyR轴的转动与直升机的偏航和俯仰运动方向相同，绕ORzR轴的转动与直升机的横滚运动方向相反。

图1 描述直升机机体和尾传轴空间运动的坐标系统

材料、加工制造工艺等因素使传动轴的质心偏离轴线，形成偏心矩。尾传动轴为跨距较大的空心薄壁结构。工作中，偏心引起的离心惯性力容易使轴产生弯曲，产生动挠度。传动轴除了绕自身轴线转动外，还会绕两端支承轴颈中心连线作涡动，轴截面将产生偏离原先平面的偏摆，即传动轴作空间运动，可分解为随基点的平移和绕基点的定点转动。在静变形状态下，取尾传动轴系水平轴左端面与传动轴支承的轴颈中心连线的交点O为原点，建立与相对坐标系ORxRyRzR的对应轴线相平行的参考坐标系Ox1y1z1。y1Oz1平面与yRORzR平面、x1Oz1平面与xRORzR平面和x1Oy1平面与xRORyR平面之间的距离分别为u0、v0和w0。传动轴的横向运动可用轴心的动挠度在参考坐标系Ox1y1z1的x1Oz1、y1Oz1两个平面上的分量u(t)、v(t)表示。轴的定点转动与基点的选择无关，仍以O点为原点建立随传动轴运动的动坐标系Oxyz，采用三个欧拉角来描述轴截面的偏摆运动，即绕Ox1轴的角ψ(t)，绕Oy2轴的角θ(t)，绕Oz轴的角φ(t)。这里的转动方向按右手法则确定，拇指方向同轴的正方向一致。

1.2 尾传动轴的能量

直升机尾传动轴有水平轴和尾斜轴，尾斜轴相对于水平轴倾斜一个角度(逆时针为正)。如图2，对于尾斜轴，建立辅助坐标系Oxbybzb，其中yb与y1重合，xb与x1及zb与z1之间的夹角φ为尾斜轴相对水平轴的倾角。当φ=0时即为水平传动轴，说明水平传动轴是尾斜轴的一种特例，取尾斜轴为研究对象更具一般性。坐标系Oxbybzb到坐标系Ox1y1z1的变换矩阵为Aφ，其表达式为

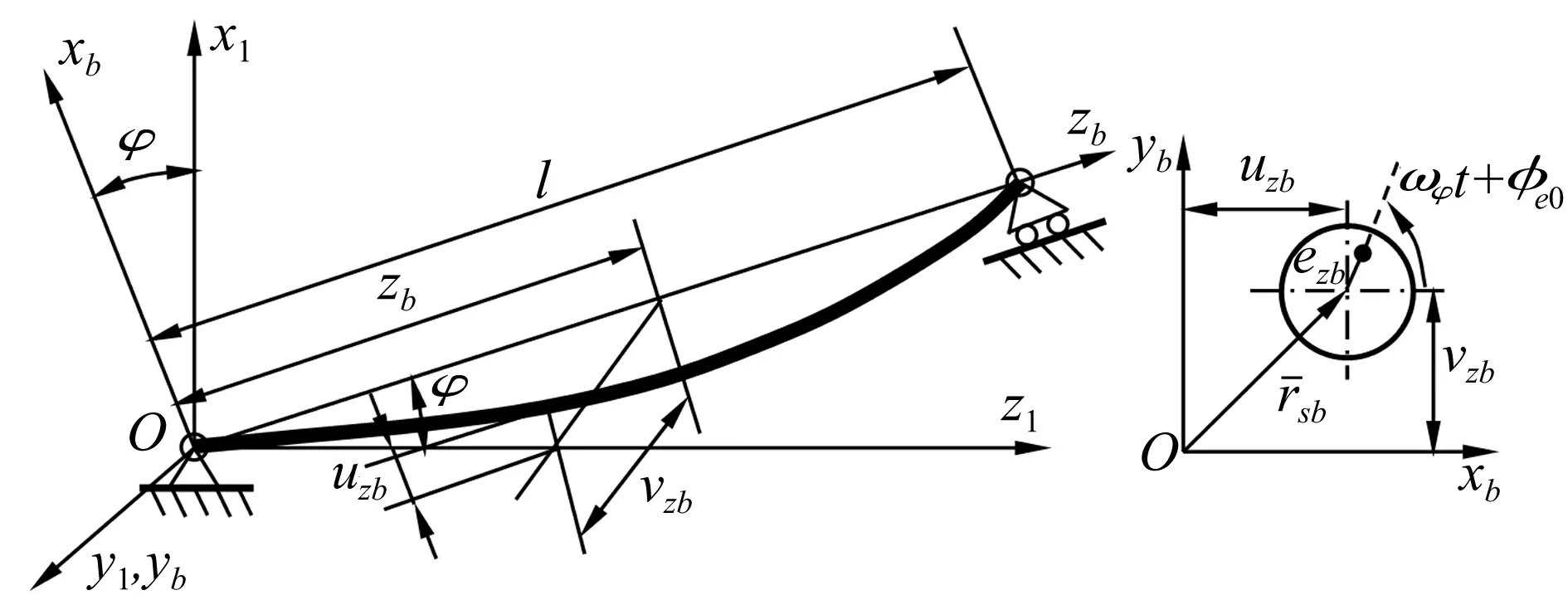
图2 尾斜轴的坐标系和瞬时位置

假设传动轴的长度为l，uzb、vzb分别为坐标为zb时轴段几何中心沿xb、yb轴的位移，轴段截面质心相对于几何中心的偏心距及其初始相位角分别为ezb、φe0，传动轴的角速度为ωφ。传动轴的动能为:

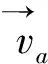
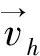
传动轴的动能由平动动能和转动动能组成，第一项为平动动能，第二项为转动动能。其平动动能为:

式中

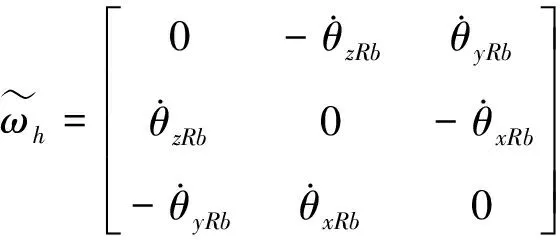
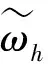
传动轴在动坐标系Oxyz中的角速度坐标矩阵[ωx，ωy，ωz]T可用欧拉角[ψ，θ，φ]T表示为:

因此，轴的总动能为:

传动轴的弹性势能为:

其中，E为传动轴材料的弹性模量，U1为轴应变引起的弹性势能，U3为重力引起的沿轴横向的势能，U2为重力引起的沿轴纵向的势能，且有:

1.3 尾传动轴系的运动微分方程

由于欧拉角ψ、θ为小量，可近似表示为:

θ=θyb+θyRb=∂uzb/∂zb+θyRb

(1)

ψ=θxb+θxRb=θxRb-∂vzb/∂zb

(2)

所以系统的拉格朗日函数可表示为:

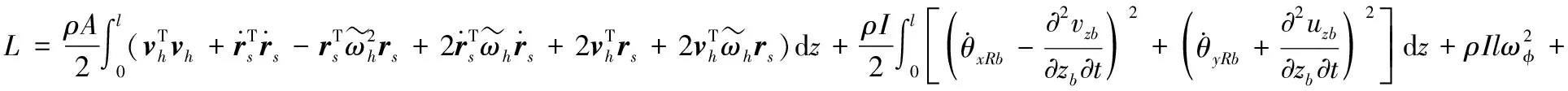
利用扩展哈密顿原理[16]，可得到传动轴的控制方程为:

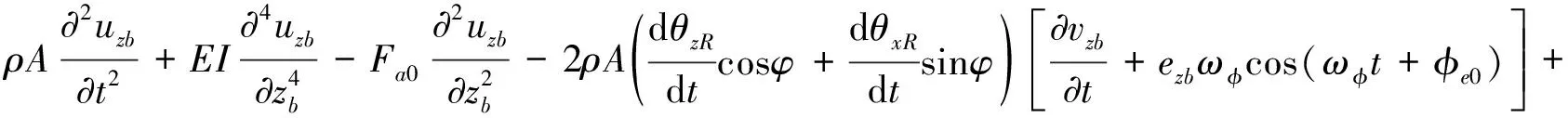
(3)

(4)

传动轴的横向位移uzb、vzb以及偏心ezb分别为

(5)

其中，Wr(zb)为传动轴的第r阶固有振型函数，是用于描述轴截面在zb处的横向振动幅值函数。qur(t)和qvr(t)是用于描述轴截面在zb处的横向振动幅值函数。ezbr轴的第r阶偏心量。

将式(5)代入式(3)和式(4)，并利用伽辽金计算方法，可以将式(3)和式(4)所表示的偏微分方程转化成如下常微分方程(r=1,2,…)

(6)

式中:

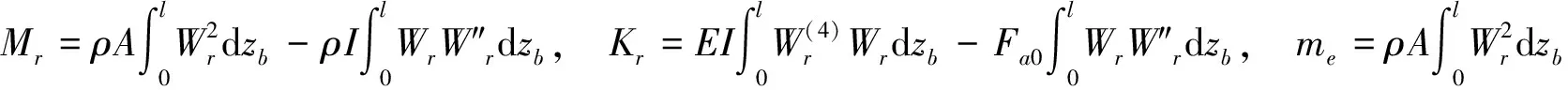
2 机动飞行对直升机尾传动轴振动特性的影响

根据式(6)可知，直升机的空间机动飞行可对尾传动轴的横向弯曲振动特性产生如下影响：

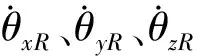
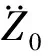
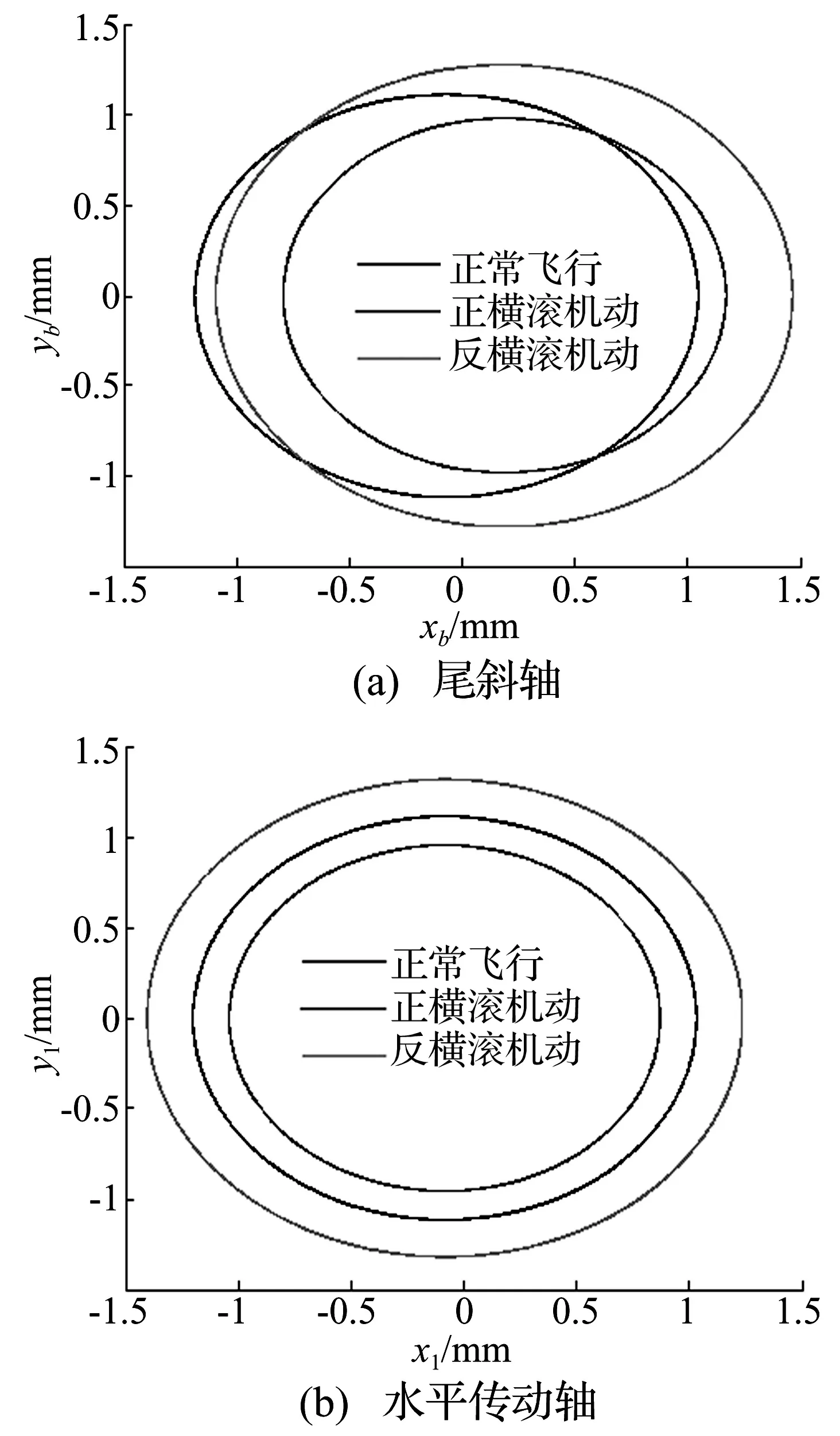
图3 横滚机动时传动轴的运动轨迹

表1 尾传动轴的计算参数

3 结 论

(1) 空间机动飞行会对尾传轴产生附加的刚度效应、阻尼效应和外激励效应。尾斜轴的影响因素相对于水平轴更复杂。

(2) 受空间机动飞行的影响，通常传动轴运动轨迹的尺寸大小和中心位置都发生变化。若只受附加阻尼效应影响，则仅改变运动轨迹尺寸的大小。

参 考 文 献

[1]Krothapalli K R, Prasad J V R, Peters D A. Helicopter rotor dynamic inflow modeling for maneuvering flight[J]. Journal of the American Helicopter Society, 2001, 46(2): 129-139.

[2]Ananthan S, Leishman J G. Rotor wake aerodynamics in large amplitude maneuvering flight[J]. Journal of the American Helicopter Society, 2006, 51(3): 225-243.

[3]林富生, 孟光. 飞行器机动飞行时发动机转子等变速运动的动力学特性研究[J]. 航空学报,2002,23(4):356-359.

LIN Fu-sheng, MENG Guang. Dynamics of a maneuvering rotor in constant acceleration and deceleration[J]. Acta Aeronautica et Ast ronautica Sinica,2002,23(4):356-359.

[4]LIN Fu-sheng, MENG Guang. Study on the dynamics of a rotor in a maneuvering aircraft[J]. Journal of Vibration and Acoustics, 2003, 125(2): 324-327.

[5]林富生, 黄其柏, 孟光. 单自由度非惯性系内转子系统的动力学特性研究[J]. 武汉理工大学学报, 2007, 31(4): 627-629.

LIN Fu-sheng, HUANG Qi-bai, MENG Guang. Journal of Wuhan University of Technology, 2007, 31(4): 627-629.

[6]徐敏, 廖明夫, 刘启洲. 机动飞行条件下双盘悬臂转子的振动特性[J]. 航空动力学报,2002,17(1):105-109.

XU Min, LIAO Ming-fu, LIU Qi-zhou. The vibration performance of the double-disk cantilever rotor in flight mission[J]. Journal of Aerospace Power, 2002, 17(1): 105-109.

[7]徐敏, 廖明夫. 机动飞行条件下带挤压油膜阻尼器的Jeffcott 转子的振动特性[J]. 航空动力学报, 2003, 18(3): 394-401.

XU Min, LIAO Ming-fu. The vibration performance of the Jeffcott rotor system with SFD in maneuver flight[J]. Journal of Aerospace Power, 2003, 18(3):394-401.

[8]顾致平, 于渊博. 飞机水平盘旋下弹性支承转子的特性研究[J]. 西安工业大学学报, 2008, 28(6): 589-593.

GU Zhi-ping, YU Yuan-bo. Investigation of rotor characteristics with elastic support in aircraft of horizontal circling[J]. Journal of Xi’an Technological University, 2008, 28(6): 589-593.

[9]惠旭升, 蔡安江, 张小龙. 转子在非惯性系中的动力学建模[J]. 机械设计, 2009, 26(7): 35-37.

HUI Xu-sheng, CAI An-jiang, ZHANG Xiao-long. Dynamic modeling of rotor in non-inertia system[J]. Journal of Machine Design, 2009, 26(7): 35-37.

[10]祝长生, 陈拥军. 机动飞行时航空发动机转子系统的振动特性[J]. 航空学报, 2006, 27(5): 825-841.

ZHU Chang-sheng, CHEN Yong-jun. Vibration characteristics of aeroengine’s rotor system during maneuvering flight[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(5): 825-841.

[11]祝长生, 陈拥军. 机动飞行时发动机转子系统动力学统一模型[J]. 航空动力学报, 2009, 24(2):371-377.

ZHU Chang-sheng, CHEN Yong-jun. General dynamic model of aeroengine’s rotor system during maneuvering flight[J]. Journal of Aerospace Power, 2009, 24(2):371-377.

[12]张群岩, 符娆, 李飞行. 机动飞行时发动机转子振动特性的工程研究[J]. 科学技术与工程, 2011, 11(26): 6498-6500.

ZHANG Qun-yan, FU Rao, LI Fei-xing. Engineering research on aero-engine rotor vibration characteristics in maneuver flight[J]. Science Technology and Engineering, 2011, 11(26): 6498-6500.

[13]杨永锋, 任兴民, 秦卫阳. 俯冲拉起下裂纹转子的非线性[J]. 振动与冲击, 2007, 26(4): 21-24.

YANG Yong-feng, REN Xing-min, QIN Wei-yang. Nonlinear response analysis of a cracked jeffcott rotor in action of dive-hike[J]. Journal of Vibration and Shock, 2007, 26(4): 21-24.

[14]杨永锋, 任兴民, 秦卫阳. 水平盘旋下裂纹转子的非线性响应[J]. 航空动力学报, 2007, 22(6):1007-1012.

YANG Yong-feng, REN Xing-min, QIN Wei-yang. Study of nonlinear response of cracked Jeffcott rotor in hovering state[J]. Journal of Aerospace Power, 2007, 22(6):1007-1012.

[15]许兆棠. 多支点传动轴动力学的研究[D]. 南京：南京航空航天大学, 2006.

[16]韩修林, 孙梅娟. 非惯性系中的哈密顿原理[J]. 宿州学院学报, 2010, 25(2):24-25.

HAN Xiu-lin, SUN Mei-juan. Hamilton’s principle in the non-inertial frame of referance[J]. Journal of Suzhou University, 2010, 25(2):24-25.