粗骨料种类对刚性弹贯穿混凝土靶剩余速度的影响
2014-09-05张兆军王晓鸣李文彬
张兆军, 王晓鸣, 李文彬
(南京理工大学 智能弹药技术国防重点学科实验室,南京 210094)
目前,针对混凝土侵彻和贯穿问题[1-2]的研究通常基于宏观尺度模型(macroscale model),即把混凝土假设为一种均匀的、各向同性的材料。在此假设下开展的研究较为广泛和深入,其中以Forrestal[3-4]、Chen[5-6]等学者的研究最具代表性。然而,实际中混凝土是一种典型的非均匀、各向异性材料,由多种介质(如粗骨料、细骨料、水泥、沙子等)和各种缺陷(如裂纹、孔穴等)组成。混凝土宏观尺度模型无法反映混凝土中各介质对混凝土力学行为的影响,这显然与实际有一定偏差。
近年来,随着细观尺度模型(mesoscale model)在混凝土材料领域的兴起和发展,一些学者开始将细观尺度模型运用于对冲击载荷下混凝土材料力学响应问题的研究。Zhou[7]通过建立混凝土细观模型,并运用有限元软件对混凝土在爆炸加载下的动态破坏进行了数值模拟。张凤国[8]采用二维有限元程序分析了骨料对混凝土侵彻及毁伤问题的影响。
本文通过编写三维随机球形粗骨料生成和投放程序,建立了混凝土三维细观有限元模型,运用有限元数值仿真方法分析了不同骨料种类对刚性弹贯穿混凝土靶后剩余速度的影响。
1 混凝土细观尺度模型
在混凝土细观尺度模型中,通常将混凝土看作是由粗骨料、水泥砂浆和两者之间的界面过渡区(ITZ, Interfacial Transition Zone)组成。基于这一思想,学者们建立了许多细观力学计算模型,如Truss模型[9]、Lattice模型[10]、连续有限元模型[7,11]等。本文通过生成随机尺寸的三维球形粗骨料并将其随机投放入混凝土基体中,建立了混凝土细观结构。然后,采用背景网格映射[12]的方法生成了由水泥砂浆、粗骨料和ITZ组成的有限元网格模型。
本研究设混凝土粗骨料的体积比为40%,骨料尺寸级配遵循Fuller曲线分布(图1),即如下关系[11]:
P(d)=100(d/dmax)n
(1)
其中,P(d)为通过网眼直径为d的筛子的骨料累计百分比,dmax为骨料最大直径,n为方程的指数。本研究根据实际中较常见的工况,取dmax=20 mm,n=0.5,从而得到骨料尺寸的级配。本文将粗骨料的形状简化为球形,并采用三维建模的方式,以更真实地描述混凝土的非均匀性。研究中,编写了三维随机球形粗骨料生成程序,以产生随机尺寸的粗骨料颗粒。

图 Fuller级配曲线
在完成粗骨料的随机生成后,需要将所有粗骨料颗粒随机地投放入混凝土基体中。为此,本文编写了三维球形骨料随机投放程序。其中,为了保证粗骨料的投放符合实际情况,需要满足如下两个条件:① 粗骨料颗粒不能与混凝土基体边界交叉或者超出边界;② 粗骨料颗粒之间不能交叉重叠。
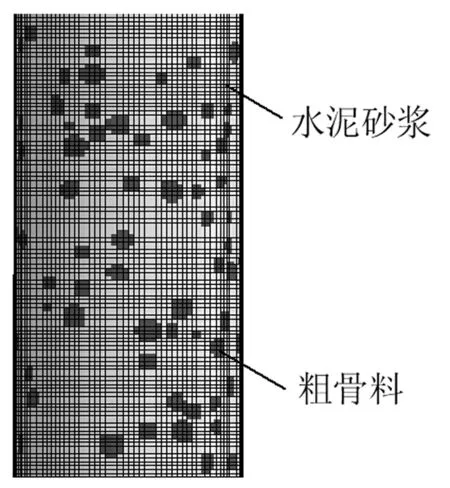
图2 混凝土细观结构网格模型
在完成随机粗骨料的生成与投放后,本文建立了三维六面体混凝土背景网格,通过背景网格与粗骨料几何轮廓的位置关系将背景网格分别映射为水泥砂浆和粗骨料两种材料的网格,并且考虑到ITZ尺度(μm级)与网格尺度(mm级)差距较大,因此将ITZ简化为水泥砂浆与粗骨料之间一种含有失效的接触,这样就避免了由于ITZ含量被过度夸大造成的失真。图2所示为通过背景网格材料识别方法生成的混凝土细观结构网格模型。
2 数值仿真
2.1 材料模型与参数取值
LS-DYNA是一种广泛用于求解大变形高应变率问题的动力有限元仿真软件,其中内嵌的材料库包含丰富的材料本构模型。本文采用连续面盖帽(CSC)模型作为水泥砂浆的材料本构模型。CSC模型作为一种混凝土材料本构模型,考虑了围压影响、三变量失效面、应变率效应以及脆韧性损伤等方面,合理性和全面性为其优点。同时,CSC模型支持程序自动拟合方式进行材料参数的设置,这又使得其具有易用性。在采用程序自动拟合方式进行参数设置时,用户只需输入无围压单轴抗压强度(FPC)、最大骨料尺寸(DAGG)和单位设置选项(UNITS)三个参数就能自动拟合生成材料的本构关系。本文中,水泥砂浆的FPC取值为50 MPa;由于细观模型只对直径大于10.0 mm的粗骨料进行了细观尺度建模,而直径小于10.0 mm的粗骨料被宏观尺度简化在水泥砂浆中,故水泥砂浆中骨料最大尺寸为10.0 mm,即为DAGG的取值;UNITS取2。

表1 粗骨料材料参数与取值
对于混凝土中的粗骨料,本文采用的为改进的Johnson-Holmquist陶瓷(JH-2)模型。这一材料模型能够较好地反映陶瓷、玻璃、岩石等脆性材料的力学行为。研究选取了花岗岩(Granite)、硅浮法玻璃(Silica float glass)和氧化铝陶瓷(Al2O3)作为粗骨料材料。表1为粗骨料的材料参数与取值[13-15]。由于JH-2模型中不含材料的无围压单轴抗压强度这一参数,为了表征不同骨料材料的强度,本文通过模拟单单元的无围压单轴压缩试验得到了三种骨料材料的无围压单轴抗压强度,如图3所示为单单元单轴数值仿真中应力与应变的关系。通常认为,材料的强度和密度是影响材料抗冲击能力的主要因素。由表1和图3可以注意到:花岗岩与硅浮法玻璃的密度较为接近,而硅浮法玻璃与氧化铝陶瓷的强度较为接近。

图3 单单元单轴压缩数值仿真中单元应力—应变关系
2.2 计算模型与方案设置
数值仿真计算采用长径比为10的长杆刚性动能合金钢弹,弹径为20.3 mm,头部形状为尖卵形,CRH(Caliber-Radius-Head)=3,质量为0.478 kg。圆柱形混凝土靶直径为51 mm,厚度为300 mm。为了节省内存,减少建模和计算时间,仿真中只对对侵彻有明显影响的区域,即混凝土靶轴心3倍弹径内的圆柱体区域进行细观尺度建模,细观区域的外围为宏观尺度模型,如图4所示。受建模试件和网格数量的限制,取六面体网格的边长为2.5 mm,由于尺寸过小的粗骨料颗粒含有的网格数太少不易控制沙漏,本文只对d≥10 mm的粗骨料颗粒建模。仿真共设置了范围从400 m/s到1 000 m/s的7组着靶速度,以分析不同着靶速度下不同骨料种类对贯穿混凝土靶后剩余速度的影响。
3 结果与讨论
图5所示为着靶速度为1 000 m/s时刚性弹贯穿三种混凝土靶后的仿真结果截面图。从中可以发现,花岗岩粗骨料混凝土的贯穿隧道孔径较另外两者更大,并且靶体中的裂纹损伤更多。氧化铝陶瓷粗骨料混凝土的贯穿隧道较另外两者更为光滑平直,靶体中的裂纹也最少。

图4 刚性弹贯穿混凝土靶的数值仿真计算模型

图5 刚性弹在着靶速度为1 000 m/s时贯穿含有不同粗骨料的混凝土靶的数值计算结果截面图

表2 不同着靶速度下刚性弹贯穿含有不同粗骨料的混凝土靶后的剩余速度

图6 剩余速度与着靶速度的关系
数值仿真计算得到了不同着靶速度下刚性弹贯穿混凝土靶后的剩余速度。如表2和图6所示,骨料种类对刚性弹贯穿混凝土靶后的剩余速度有一定的影响。其中,若将着靶速度分为三段则剩余速度呈现不同的现象。① 着靶速度为400~600 m/s时,贯穿氧化铝陶瓷和硅浮法玻璃粗骨料混凝土的弹体剩余速度较为接近并且低于花岗岩粗骨料混凝土。此时着靶速度较低,强度是影响材料抗贯穿能力的主要因素,强度越大则材料的抗贯穿能力越强,而密度对材料抗贯穿能力的影响不明显。② 着靶速度为600~800 m/s时,贯穿三种粗骨料混凝土的弹体剩余速度彼此间较为接近。此时随着着靶速度的增大,强度对材料抗贯穿能力的影响减弱,而密度对材料抗贯穿能力的影响依然不明显。③ 着靶速度为800~1 000 m/s时,贯穿硅浮法玻璃和花岗岩粗骨料混凝土的弹体剩余速度较为接近并且高于氧化铝陶瓷粗骨料混凝土。此时随着着靶速度进一步增大,强度对材料抗贯穿能力的影响进一步减弱,而密度对材料抗贯穿能力的影响增强,并成为主要影响因素,密度越大则材料抗贯穿能力越强。
另外,本文仿真结果还与Chen[6]提出的刚性弹贯穿混凝土靶剩余速度计算模型进行了对比,如图6所示。对比表明:在速度较低时,仿真结果与计算模型有一定偏差,这是由于计算模型本身的局限性[6]所造成的;在中高速段,数值仿真结果与计算模型吻合较好,有较高的仿真精度。
以上结果可应用于混凝土防护结构的设计。当设计抗低速冲击的混凝土防护结构时,可以将重点放在提高粗骨料材料的强度上;而设计抗高速冲击的混凝土防护结构时,可以将重点放在提高粗骨料材料的密度上。
4 结 论
本文建立了三维混凝土细观模型,利用连续有限元软件对刚性弹贯穿含有不同种类粗骨料的混凝土靶问题进行了数值仿真计算,分析了粗骨料种类对不同着靶速度下弹体贯穿混凝土靶后剩余速度的影响。当着靶速度较低时,粗骨料的强度是影响剩余速度的主要因素,强度越高剩余速度越低,反之则越高;当着靶速度较高时,粗骨料的密度是影响剩余速度的主要因素,密度越高剩余速度越低,反之则越高。分析结果可为混凝土防护结构的设计提供参考依据。
参 考 文 献
[1]陈小伟. 穿甲/侵彻问题的若干工程研究进展[J]. 力学进展,2009, 39(3): 316-351.
CHEN Xiao-wei. Advances in the penetration/perforation of rigid projectiles[J]. Advances in Mechanics, 2009, 39(3): 316-351.
[2]纪冲,龙源,周望远. 弹丸冲击贯穿有限厚混凝土材料靶板的背面成坑效应[J]. 振动与冲击, 2013, 32(4): 85-89.
JI Chong, LONG Yuan, ZHOU Wang-yuan. Rear face crater-forming of a limited-thickness concrete target due to projectile penetrating[J]. Journal of vibration and shock, 2013, 32(4): 85-89.
[3]Forrestal M J, Tzou D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International Journal of Solids and Structures, 1997, 34(31-32): 4127-4146.
[4]Forrestal M J, Altman B S, Cargile J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4): 395-405.
[5]Chen X W, Li X L, Huang F L, et al. Damping function in the penetration-perforation struck by rigid projectiles [J]. International Journal of Impact Engineering, 2008, 35(11): 1314-1325.
[6]Chen X W, Fan S C, Li Q M. Oblique and normal perforation of concrete targets by a rigid projectile[J]. International Journal of Impact Engineering, 2004, 30(6): 617-637.
[7]Zhou X Q, Hao H. Mesoscale modelling and analysis of damage and fragmentation of concrete slab under contact detonation[J]. International Journal of Impact Engineering, 2009, 36: 1315-1326.
[8]张凤国,刘 军,梁龙河,等. 数值建模时骨料对混凝土侵彻及毁伤问题的影响[J]. 爆炸与冲击,2013, 33(2): 217-220.
ZHANG Feng-guo, LIU Jun, LIANG Long-he, et al. Influence of aggregate on penetration process of concrete target when numerical modeling[J]. Explosion and shock waves, 2013, 33(2): 217-220.
[9]Bazǎnt Z P, Tabbara M R, Kazemi M T, et al. Random particle model for fracture of aggregate or fiber composites[J]. Journal of Engineering Mechanics, 1990, 116(8): 1686-1705.
[10]Schlangen E, Mier J G M. Simple lattice model for numerical simulation of fracture of concrete materials and structures[J]. Materials and Structures,1992, 25(9): 534-542.
[11]Wriggers P, Moftah S O. Mesoscale models for concrete: Homogenisation and damage behaviour[J]. Finite Elements in Analysis and Design, 2006, 42(7): 623-636.
[12]唐欣薇,秦川,张楚汉.基于细观力学的混凝土类材料破损分析[M].北京:中国建筑工业出版社,2012.
[13]Ai H A, Ahrens T J. Simulation of dynamic response of granite: A numerical approach of shock-induced damage beneath impact craters[J]. International Journal of Impact Engineering, 2006, 33(1-12): 1-10.
[14]Anderson C E, Johnson G R, Holmquist T J. Ballistic experiments and computations of confined 99.5% Al2O3 ceramic tiles: Proceedings of the 15th International Symposium on Ballistics[Z]. Israel, Jerusalem, 1995, 2:65-72.
[15]Holmquist T J, Johnson G R, Grady D E, et al. High strain rate properties and constitutive modelling of glass: Proceeding of Fifteenth International Symposium on Ballistcs[Z]. Jerusalem, Israel: 1995.
