基于小波包能量曲率差的古木结构损伤识别

王 鑫， 胡卫兵, 孟昭博

(1.西安建筑科技大学 土木工程学院, 西安 710055; 2聊城大学 建筑工程学院, 山东 聊城 252000)

我国是文明古国，古建筑是重要的历史文化遗产组成部分，是中华民族的瑰宝。西安钟楼位于东、西、南、北四条大街交汇处，是西安的标志性建筑，是国家重点保护文物。上世纪80年代地面交通引起的微幅振动使钟楼二层地板上的展品发生移位，高台基的墙体和木构架的横梁裂缝不断扩展。虽然钟楼环道内侧至高台基边缘的距离扩大到26.7 m，车辆引起的振动对钟楼的影响有增无减，钟楼二层地板有明显的振感。西安是西部发展重心，现代工业迅速发展，人口不断增加，地面交通流量不断增大，为从根本上缓解地面交通压力，西安市规划建设6条地铁线路，总长达251.8 km，钟楼四侧有四条隧道穿过，距离钟楼仅15 m。对古木结构来说，交通环境振动是历经数百年古建木结构寿命新威胁，也是正常情况下经受的最严重的威胁，长期的交通环境微振动能使木结构疲劳、榫卯松动、结构变形、寿命缩短。钟楼一旦遭到破坏，不可再生，造成历史文化遗产不可弥补的损失，这就要求结构健康监测与安全评估系统及时发现损伤并在第一时间预警。因此利用环境激励下的结构振动响应对结构进行健康监测，已是结构健康监测中损伤检测的新研究方向，同时对保护古建筑有着积极意义。

通常的损伤识别系统分为四个阶段: ① 损伤是否存在; ② 损伤位置判定; ③ 损伤的严重程度; ④ 结构的实用性预测。损伤识别方法分为局部和整体两种方法。目前有直观判定、超声波、电磁场及电涡流等检测方法，需预先知道损伤的大体位置,对损伤部位进行仪器操作，整体损伤识别通过结构振动特性的变化评价结构的健康情况,只有将两者结合起来,才能准确评价复杂结构的健康状况[1-2]。传统的模态参数频率和振型不能准确识别损伤,大多数损伤评估方法通过对瞬态信号的傅里叶变换得到模态参数，而傅里叶变换的最大缺陷是对高频模态分析不足。小波分析被誉为数学显微镜,本身具有放大、缩小和平移等功能,可通过检查不同放大倍数下的变化来研究信号的特征,具有优良的时频局部化特性，但有高频段分辨率差的缺点。小波包分析是小波变换的扩充,能为信号提供一种更加精细的分析方法, 将小波分析没有细分的高频部分进一步分解, 具有任意的时-频分辨率，根据分析信号的特征选择相应的频带,使之与信号频谱匹配。因此小波包分析在土木工程结构的健康监测与损伤诊断中具有非常广阔的应用前景。

20世纪80年代开始，国内外学者开展了小波包分析在结构损伤诊断领域中的应用研究，取得了一定的研究成果。丁幼亮等[3]对Benchmark 钢框架结构试验数据和润扬大桥悬索桥监测数据进行小波包能量谱损伤预警分析，在此基础上详细考察了不同小波函数和小波包分解层次的损伤预警效果。刘涛等[4]做了基于小波包能量谱的结构损伤预警方法试验研究。邓扬等[5]采用小波包分析进行了拉索损伤声发射信号特征提取。范颖芳等[6]利用小波包对不同损伤情况下拱桥结构的观测信号分析，确定了结构异常状态的敏感特征。韩建刚等[7]提出了小波包变换的能量变化率指标对梁体进行了损伤识别的定位研究，并进行试验验证。余竹等[8]利用沧州子牙河新桥替换下的梁体进行两种工况损伤模拟，用小波包能量曲率差法识别损伤，考察小波函数和分解层数对识别效果的影响。

本文以西安钟楼为工程依托，提出小波包能量曲率差对古木结构进行损伤定位识别，把有限元分析得到梁上各节点的加速度响应信号进行小波包分解，计算该指标进行损伤定位，该指标对于损伤识别比较敏感,能准确判定古木结构损伤的具体位置。

1 小波包分析

小波包由一系列线性组合小波函数组成：

(1)

式中，i，j，k分别表示频率因子、尺度因子和平移因子。

小波函数ψi递推关系式为:

(2)

(3)

式中:ψ表示小波母函数，h(k)和g(k)为与尺度函数及小波母函数相关的积分镜像滤波器系数。

对于任意信号的第j阶和第j+1阶水平小波包分解递推关系为:

(4)

(5)

(6)

其中，H和G分别为h(k)和g(k)构成的滤波算子，

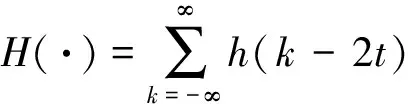
(7)

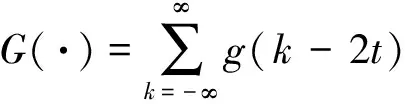
(8)

经过j水平的小波包分解后，初始信号f(t)为:

(9)

(10)

小波包系数为:

(11)

小波包系数满足正交条件:

(12)

小波包信号能量为:

(13)

将式(10)代入式(13)，并利用式(12)得到：

(14)

(15)

小波包组分能量对信号的变化十分敏感，可用于结构的损伤识别。

2 古木结构的损伤识别

本文把古木结构的损伤识别分为两部分:① 对古木结构梁上各节点的加速度响应信号进行小波包分解；② 计算小波包能量曲率差进行结构的损伤定位识别，其中包括小波函数和小波包分解层次的选择。

2.1 合理的选择小波函数

从消失矩和支撑长度考虑，选用Daubechies为小波函数，简记为dbN(N为阶次)。N越大，Daubechies小波的消失矩越高，时域的分辨率越好；但同时Daubechies小波支撑长度越宽，小波的时域局域性越差。因此应合理确定Daubechies小波阶次N。

对结构动力响应f(N,k)进行第i层小波包分解,fij表示第i层分解节点(i,j)的结构响应,每个频带内结构响应fij能量[9]:

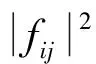
(16)

则结构动力响应f(N,k)第i分解层的小波包能量谱向量Ei:

(17)

为衡量小波函数好坏，定义i分解层各频带能量系数系列{Eij}的代价函数M{Eij}。小波包能量谱中各频带能量系数Eij的时频集中程度由代价函数M{Eij}反映。采用lp范数熵为代价函数，在同一小波包分解层上，计算不同小波函数的代价函数值并比较，确定较适合的Daubechies小波阶次N。通常不同的阶次计算小波函数的代价函数值越小越好,lp范数熵(1≤p≤2)定义为[9]：

(18)

2.2 合理的选择小波包分解层数

在工程应用中，对结构动力响应进行小波包分解，计算每一分解层次上的小波包能量谱的代价函数，从代价函数和计算时间考虑确定适当的小波包分解层次，通常小波包能量谱代价函数值越小，计算机计算过程耗时越少，小波包分解层次越好。类似小波函数阶次的选择方法，采用lp范数熵为代价函数，确定合适的小波包分解层数，lp范数熵(1≤p≤2)定义[9]：

(19)

2.3 不等间距曲率求解方法[8]

在实际工程中，曲率一般由变量的二阶差分(斜率的变化率)得到。

不等间距情况下曲率求解式为:

(20)

式中:分子为节点左右两段曲线斜率差，分母为节点左右两端斜率差间距。若节点等间距，hi-1=hi+1，则:

式(21)为二阶差分法求解等间距曲率公式。 将式(21)中y换成小波包能量谱，则为小波包能量曲率。将完好状态与损伤状态各节点的小波包能量曲率进行插值，得到损伤状态的小波包能量曲率差为:

(22)

3 算例

3.1 古木结构的有限元模拟

本文以西安钟楼为工程依托，选取其中一榀框架进行分析。通过Ansys有限元软件对环境激励下古木结构进行损伤模拟分析，以钟楼为参考，选取木框架计算参数，选取木梁长4 m,木柱高6 m,梁截面尺寸为300×700 mm2，柱截面直径500 mm，用beam188梁单元模拟木柱、木梁，用combin14单元模拟榫卯节点，榫卯连接的弯曲刚度为[10]：1×1010kN·m/rad，木材的弹性模量取1×1010N/m2，泊松比为0.25，密度为410 kg/m3，采用Rayleigh定义的粘性比例阻尼。柱子搁置在有凹槽的柱础上，不能完全限制柱子转动，在荷载引起的微幅振动下不计其线位移，柱与基础的连接简化成固定铰支座的力学模型符合实际情况[11-12]，建立古木结构的有限元模型如图1所示。

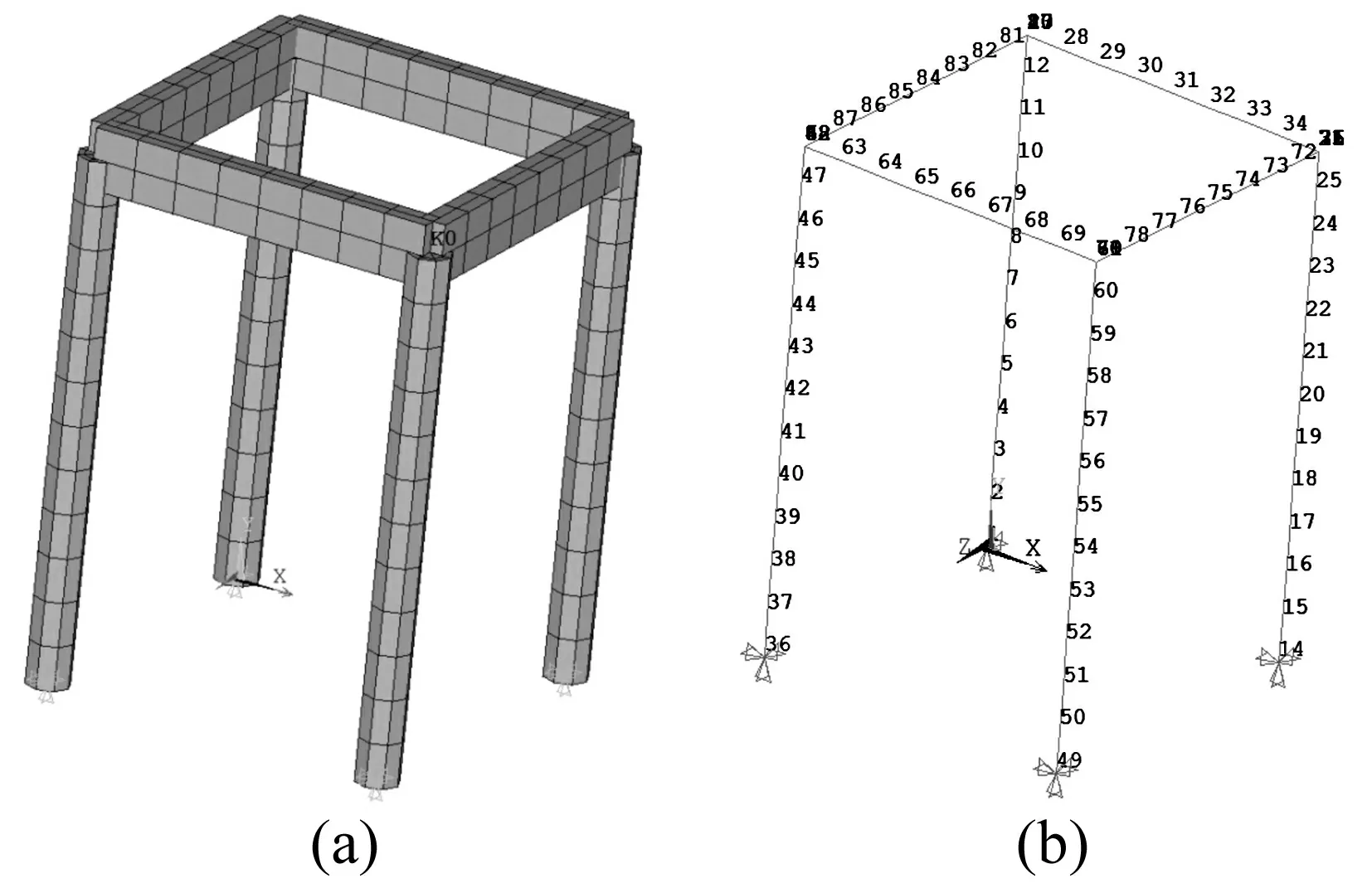
图1 古木结构的有限元模型(a)和节点详图(b)

西安钟楼处于地面交通和地铁运行的复杂交通环境下，地面交通振动通过高台基传播引起钟楼振动，运行的地铁对轨道产生的冲击作用产生振动，通过隧道结构传到周围地层，并经过地层向周围传播激励钟楼产生振动，因而在该木框架的柱底节点1处沿x轴正方向施加随机激励荷载来模拟环境激励对钟楼的影响[13]，随机激励荷载的时程曲线及频谱如图2所示，获得结构的加速度荷载时程，在此基础上运用Matlab程序计算了小波包能量谱。

古木结构的损伤程度通过折减损伤单元的弹性模量来实现，其中10%、18%、20%分别指损伤单元的弹性模量减少10%、18%、20%[9]，如表1所示。

对损伤工况1、2进行分析，得出完好结构和损伤工况1、2梁跨中第31节点的竖向加速度时程曲线如图3所示。从图3看出各损伤工况的信号有细微差别，但很难判断古木结构的损伤情况。因此下面采用小波包能量曲率差对古木结构进行损伤识别。

图2 激励荷载的时程曲线(a)和频谱曲线(b)

表1 古木结构损伤工况

3.2 选择计算参数

3.2.1 小波函数的选择

梁跨中挠度较大，是易出现损伤部位，因而对完好结构梁跨中第31节点的竖向加速度响应，选择不同阶次的Daubechies进行小波包分解，分解层次取4，计算lp范数熵代价函数值如表2所示。从表2看出，当小波阶次为20时，lp范数熵为5 592.46，其值相对其他小波阶次最小，因此损伤识别小波函数选择Daubechies20。

图3 第31节点加速度响应

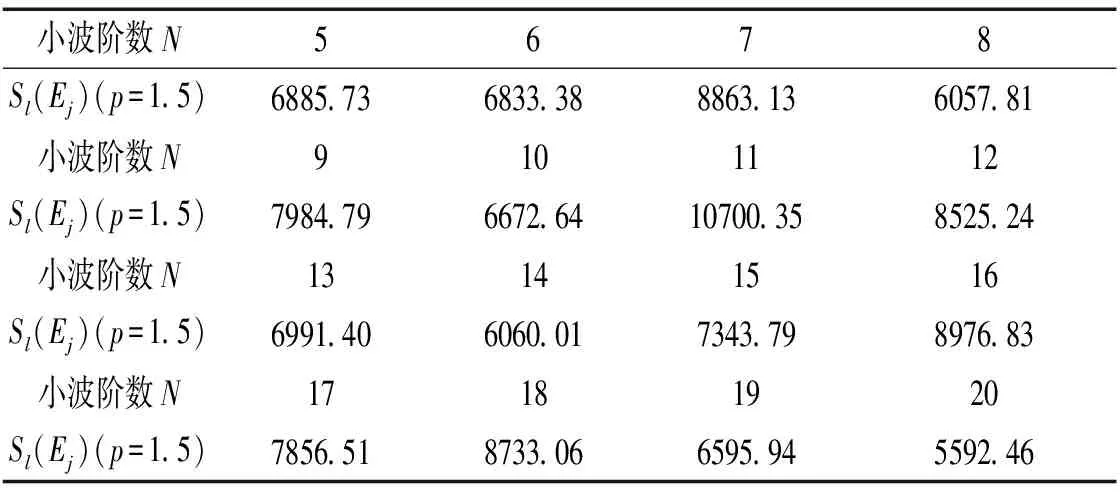
表2 分解层次为4时不同db小波的代价函数值

3.2.2 小波包分解层数的选择

采用Daubechies20对梁跨中第31节点完好状态下的竖向加速度响应进行小波包分解，分解层次取1～8，计算lp范数熵的代价函数值，并记录计算机计算耗费的时间如表3所示。从表3看出，当小波包分解层次为4时代价函数值为5 592.46,计算机计算时间为0.109 s，代价函数和计算时间均相对较小，因此损伤识别小波包分解层次取4。

表3 Daubechies 20 不同分解层次的代价函数值和计算时间

注:计算机的CPU为Intel (R) Core(TM) i5 M2430 2.40 GHz。

3.3 损伤识别

3.3.1 自振频率

为了研究古木结构不同损伤程度的损伤识别指标,列出完好结构、损伤工况1、损伤工况2的自振频率f0、f1、f2见表4所示。

从表4可以看出古木结构的损伤对自振频率的影响非常小,损伤工况1与完好结构的自振频率最大误差仅为0.63%，损伤工况2与完好结构的自振频率最大误差仅为1.39%，看来利用结构自振频率的变化来发现古木结构的损伤十分困难,因此本文提出了基于小波包能量曲率差的损伤识别指标。

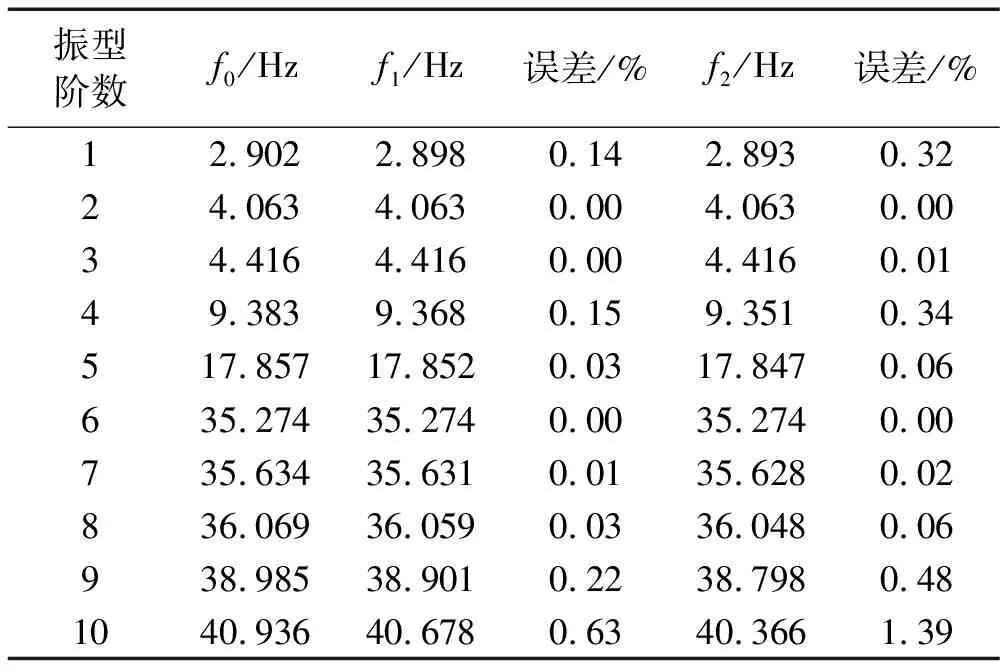
表4 古木结构的自振频率

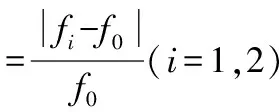
3.3.2 小波包能量曲率差

(1) 损伤工况1的小波包能量曲率差

对古木结构损伤工况1损伤前后梁上27到35节点的竖向加速度响应进行小波包分解，选择小波函数Db20，分解层数为4层，得到16个小波包系数和能量值，分析前8个能量的小波包能量曲率差如图4所示。

从图4(b)、(f)、(i) 可以看出，损伤工况1的损伤发生在30到32节点之间的损伤单元52、53位置，这正好是梁假定的损伤单元52、53所在位置，与损伤工况1假定的损伤位置完全吻合，可以判定在此位置发生了损伤，说明小波包能量曲率变化量可以用于古木结构的损伤定位。

由于篇幅有限，损伤工况2损伤前后的小波包能量曲率差就不一一列举了。

(2)损伤工况1、2的小波包能量曲率差(前8个分量叠加)。

从图4看出损伤工况1的小波包能量曲率差的前8个能量图中只有部分图形能确定结构的损伤位置，在此基础上将损伤工况1、2的小波包能量曲率差前8个分量进行叠加来分析损伤定位的效果如图5所示。

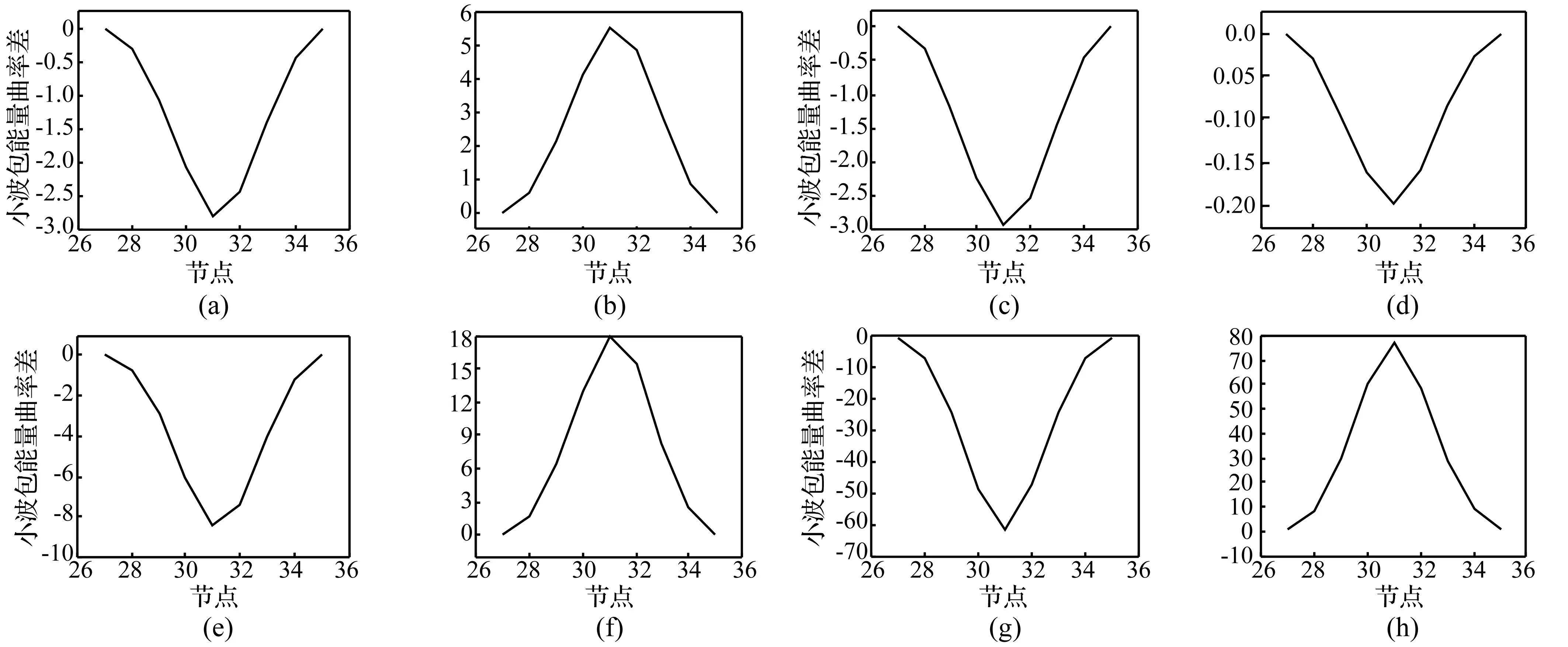
图4 损伤工况1的小波包能量曲率差

由图5(a)、(b)看出，将损伤工况1、2损伤前后的小波包能量曲率差的前8个分量进行叠加，在节点31处发生突变，其值最大，损伤位置最明显，随着节点离跨中越远，损伤指标值越小，到梁两端的27和35节点时，损伤指标值达到最小，说明该指标对损伤位置较敏感，小波包能量曲率差的前8个分量叠加比小波包能量曲率差更能识别古木结构的损伤位置，它可以作为损伤识别指标进行古木结构的准确定位，并且损伤程度越大，该指标值越大。

3.4 噪声对损伤识别的影响

在结构的健康监测过程中,由传感器采集的数字信号难免要受到外界噪声的干扰，对于信号中存在的噪声,一般假定为高斯白噪声,在原有信号基础上叠加服从正态分布均值为0的量作为测量噪声,通过信号的信噪比(SNR)来衡量信号的噪声水平,信噪比定义为:

(23)

式中：AS为信号x(n)的均方根，AN为噪声y(n)的均方根。

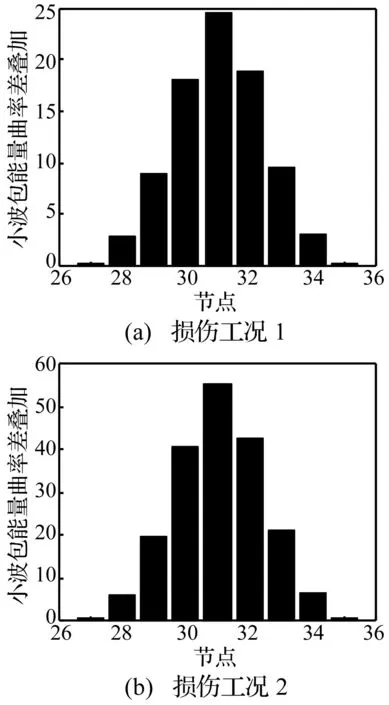
图5 损伤工况1、2的小波包能量曲率差叠加

下面以损伤工况1为例来分析在信噪比SNR=10、20、30、40、50情况下对损伤定位效果的影响。在有限元分析得到的梁上各节点的竖向加速度信号中分别加入不同分贝的高斯白噪声来研究噪声对损伤识别的影响。仍选用db20小波函数进行小波包分解,分解层数为4，不同噪声水平下的小波包能量曲率差的前8个分量叠加如图6所示。

从图6看出测试数据含有白噪声对信号的高频部分影响较大,故在含噪信号的小波包分解中应选用低频概貌信号和低频细节信号作为损伤识别的判别依据。当信噪比SNR小于或者等于20 db时, 该损伤指标受噪声影响较大,对损伤定位效果影响较大,已不具备损伤定位的能力。当信噪比SNR等于30 db时，受噪声影响较小，已能基本进行损伤定位了。当信噪比SNR大于或者等于40 db时, 损伤定位能力已不受噪声影响，该损伤指标对损伤定位效果与无噪声信号基本相当,说明随着信噪比的提高, 该损伤指标对损伤识别的敏感性逐渐增加，损伤定位效果越好，该损伤指标具有一定的抗噪声干扰能力。当信噪比较小时,受噪声的影响较大,因此需对含噪声信号进行消噪处理,尽可能还原为原始信号,才能保留损伤信息，以便对古木结构的损伤进行准确定位。

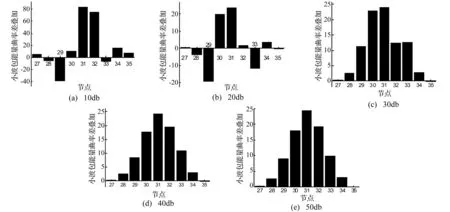
图6 不同噪声水平下小波包能量曲率差叠加

3.5 损伤程度的判定

由图5看出, 对于无噪声信号在同一损伤位置不同损伤程度时，损伤指标柱状图基本相似,只是数值大小有差别。因此设想对于同一损伤位置不同损伤程度，若能找到损伤程度和损伤指标之间的函数关系，绘出其关系曲线，就能由该关系曲线对损伤程度进行判断了。

损伤程度的判定方法:首先判定结构是否存在损伤,若存在损伤，再确定损伤的具体位置,然后针对该损伤位置,对不同损伤工况进行数值模拟,得到损伤位置上不同损伤工况下的损伤指标,再运用matlab进行数值拟合,绘出损伤指标与损伤程度之间的关系曲线,由该关系曲线判定该损伤位置的损伤程度。

仍假设古木结构梁跨中出现损伤,对梁跨中损伤程度10%、15%、20%、25%、30%、35%、40%、45%、50%各损伤工况进行有限元分析,得到梁上各节点的竖向加速度信号，计算梁跨中31节点的损伤指标—小波包能量曲率差的前8个分量叠加如表5所示，采用matlab进行数值拟合，找到损伤位置31节点处损伤程度和损伤指标之间的函数关系，绘制其函数关系曲线如图7所示。

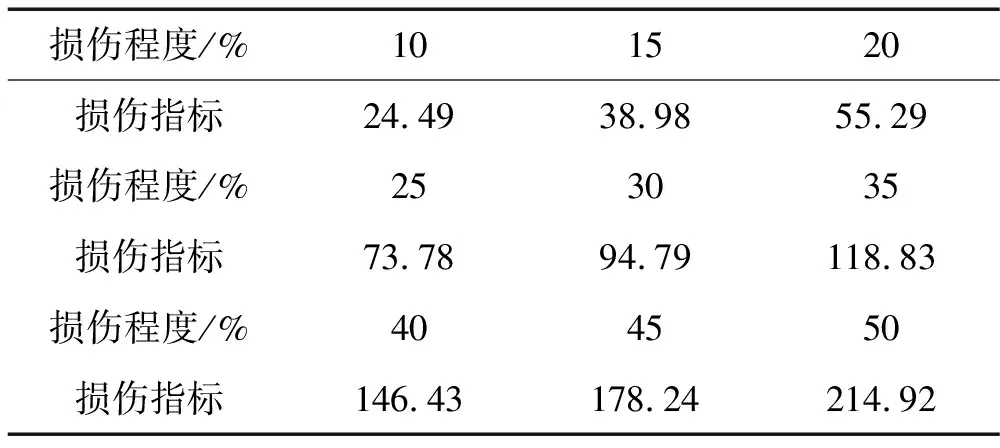
表5 损伤指标

图7 损伤程度和损伤指标之间的关系曲线

从图7得出损伤指标和损伤程度之间的函数关系式为:y=0.062 36x2+0.947 9x+10.13，对古木结构损伤前后进行有限元模拟，得到梁上各节点的竖向加速度信号进行小波包分解，求出损伤指标,由该损伤指标就能在图7中找到相应的损伤程度了。

图8 损伤工况3的损伤指标

下面验算其适用性：假设梁跨中损伤程度为18%,对损伤工况3进行数值分析,得到梁上各节点的竖向加速度响应信号进行小波包分解,计算并绘制损伤指标如图8所示，得到31节点的损伤指标y= 48.53,由图7可以逆推出x=18.35%,其相对误差为1.9%,可见其误差非常小，因此该函数关系式能对古木结构的损伤程度进行较准确的识别。

4 结 论

本文以西安钟楼为工程依托，对随机激励作用下的古木结构梁上各节点的加速度响应信号进行小波包分解,提出了小波包能量曲率差损伤识别指标,通过此指标进行古木结构的损伤定位，得出结论：

(1) 在无噪声干扰下，该损伤指标对于古木结构的损伤定位比较敏感,可以准确判定古木结构的损伤位置，并且损伤指标随损伤程度的加大而增大。

(2) 该损伤指标在高斯白噪声干扰下,当信噪比SNR大于或者等于40 db时，损伤识别能力已不受噪声影响，能对古木结构的损伤进行准确定位,说明该损伤指标具有一定的抗噪声干扰能力,在实际工程应用中能够取得较好的定位识别效果。

(3) 得出了损伤指标和损伤程度之间的函数关系式，用其进行损伤程度的判断并验算其适用性，为研究环境激励下西安钟楼的损伤预警提供了理论依据。

参 考 文 献

[1]Coifman R R, Wickerhauser M V. Entropy-based algorithms for best basis selection [J]. IEEE Trans. Inf. Theory, 1992, 38:713-718.

[2]Doebling S W, Farrar C R, Prime M B. A summary review of vibration-based damage identification methods [J]. Shock Vib.Dig, 1998, 30(2): 91-105.

[3]丁幼亮,李爱群,邓扬. 面向结构损伤预警的小波包能量谱识别参数[J].东南大学学报(自然科学版), 2011,41(4):824-828.

DING You-liang, LI Ai-qun, DENG Yang. Parameters for identification of wavelet packet energy spectrum for structural damage alarming[J]. Journal of Southeast University (Natural Science Edition), 2011,41(4):824-828.

[4]刘涛,李爱群,丁幼亮,等. 基于小波包能量谱的结构损伤预警方法试验研究[J]. 振 动 与 冲 击，2009,28(4)：4-9.

LIU Tao, LI Ai-qun, DING You-liang, et al. Experimental study on structural damage alarming method based on wavelet packet energy spectrum[J]. Journal of Vibration and Shock,2009,28(4)：4-9.

[5]邓扬,丁幼亮,李爱群.基于小波包分析的拉索损伤声发射信号特征提取[J].振 动 与 冲 击，2010，29(6)：154-158.

DENG Yang, DING You-liang, LI Ai-qun. Feature extraction of acoustic emission signals for cable damage based on wavelet packet analysis[J]. Journal of Vibration and Shock, 2010，29(6)：154-158.

[6]范颖芳，胡志强，周晶,等. 基于小波包分析的肋拱桥结构损伤状态研究[J].工 程 力 学，2008,25(5)：182-188.

FAN Ying-fang, HU Zhi-qiang, ZHOU Jing, et al. Study on damage state of ribbed arch bridge using wavelet packet analysis [J]. Engineering Mechanics, 2008,25(5)：182-188.

[7]HAN Jian-Gang, REN Wei-Xin, SUN Zeng-Shou. Wavelet packet based damage identification of beam structures [J]. International Journal of Solids and Structures, 2005,42: 6610-6627.

[8]余竹，夏禾, Goicolea J M,等. 基于小波包能量曲率差法的桥梁损伤识别试验研究[J]. 振动与冲击,2013,32(5)：20-25.

YU Zhu，XIA He，Goicolea J M, et al. Experimental study on bridge damage identification based on wavelet packet energy curvature difference method [J]. Journal of Vibration and Shock, 2013,32(5)：20-25.

[9]李爱群,丁幼亮.工程结构损伤预警理论及其应用[M].北京:科学出版社, 2007.

[10]孟昭博.西安钟楼的交通振动响应分析及评估[D].西安：西安建筑科技大学，2009.

[11]孟昭博, 袁俊, 吴敏哲,等. 古建筑高台基对地震反应的影响[J]. 西安建筑科技大学学报(自然科学版), 2008,40(6):835-840.

MENG Zhao-bo,YUAN Jun,WU Min-zhe, et al. The influence of high-station base of ancient building on its seismic responses [J]. J.Xi’an Univ. of Arch. & Tech(Natural Science Edition), 2008, 40(6):835-840.

[12]赵均海，俞茂宏，高大峰,等.中国古代木结构的弹塑性有限元分析[J].西安建筑科技大学学报，1999,31(2):131-133.

ZHAO Jun-hai, YU Mao-hong, GAO Da-feng, et al. FEM analysis on the elasto-plasticity of ancient wooden structure [J]. J.Xi’an Univ. of Arch. &Tech, 1999, 31(2):131-133.

[13]韩广森.城市轨道交通微幅振动对古建筑的影响[D].西安：西安建筑科技大学，2011.