基于磁流变阻尼器的结构损伤模拟试验研究

林友新, 贾子光， 任 亮， 李宏男， 成明涛, 张 鹏

(1. 广东电网公司 电力科学研究院, 广州 510080; 2. 大连理工大学 建设工程学部, 大连 116024)

结构健康监测及损伤识别是当前学术界和工程界研究的热点问题之一。为保证结构在服役期内安全使用，防止结构突然失效，应及时对结构的健康状态做出判断。目前，已有的各种损伤识别方法多以振动测试为基础，通过分析比较结构损伤前后动力特性的变化来实现。这种方法需要准确判断损伤发生的时间，在此基础上进行结构模态参数识别[1-2]。

目前大多数研究成果停留在理论研究层面，试验验证较少。原因在于，结构健康诊断与损伤识别的验证性试验需要在试验前对构件进行破损处理，即通过削减构件截面面积减小构件刚度，而试验构件破损后不可复原，从而不便于进行重复性试验，使结构损伤识别试验周期长、费用高，并且少量破损构件的试验数据离散性大，难以对理论方法的正确性进行充分支持[3]。另一方面，为了在结构动力模型试验中模拟构件发生突然损伤，进而判断损伤时间，需要在结构动力加载过程中改变构件的刚度。而如果通过削弱截面的方式减小刚度，则必然与结构构件接触，改变结构的受力状态。现在尚没有一种能够在模型试验动力加载过程中，瞬时改变构件刚度的有效方法。

根据上述问题，本文提出一种利用磁流变阻尼器模拟受压构件刚度折减的试验方法。将磁流变阻尼器通过连接铰安装在受压构件内，通过改变磁流变阻尼器通电电流来调整受压构件的抗压刚度的大小。在不替换试验构件的情况下，该方法可实现多种损伤工况的模拟。在输电塔桁架动力模型试验中，利用该方法进行了受压构件刚度瞬时折减的尝试性实验,结合短时傅里叶变换等信号处理方法，对损伤时间进行判别，验证了该方法的有效性。

1 装有磁流变阻尼器的受压构件

1.1 磁流变阻尼器简介

磁流变阻尼器是一种可以通过对输入电流的调节，控制其阻尼力大小的装置，且具有体积小、响应快等优点，目前已应用于斜拉桥、海洋平台等结构的隔振、减震控制中。有关研究表明，磁流变液在不同应用电流作用下压缩模量不同，电流增加引起的磁场增强，会使其压缩弹性模量显著增大[4-8]。

利用磁流变阻尼器弹性模量随通电电流改变这一特点，将磁流变阻尼器以一定的连接方式安装在受压构件内，即可通过改变电流的方式，人为控制受压构件的整体抗压刚度。且磁流变阻尼器具有响应快的特点，可以准确控制其通电电流变化的时间，进而模拟抗压刚度在指定时间发生突变。

1.2 磁流变阻尼器安装方式

图1为装有磁流变阻尼器受压杆件的示意图。假定原始受压杆件的总长度为L，截面面积为A。按照磁流变阻尼器的形状，将原始受压构件的中间部分切除，并在切除部分的两端设置连接铰。将磁流变阻尼器装入切除部分，并固定在两个连接铰之间。这样，在构件受压力作用时，磁流变阻尼器不会产生由于安装偏心引起的弯矩作用。

图1 磁流变阻尼器安装

1.3 装有磁流变阻尼器受压构件的整体弹性模量

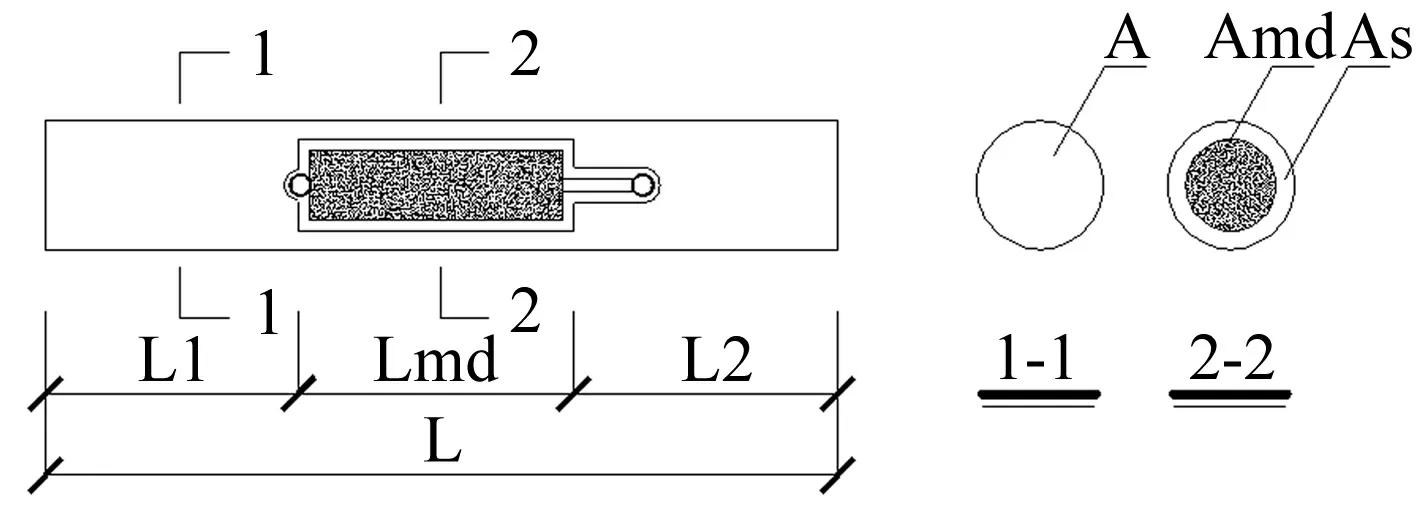
图2 装有磁流变阻尼器受压构件的几何参数

受压构件的总长度为L，截面面积为A，如图2所示。原始材料弹性模量为Es，轴向压力为F，磁流变阻尼器的截面面积、弹性模量和长度分别为Amd、Emd和Lmd；磁流变阻尼器所在断面的原始构件截面面积为As，磁流变阻尼器以上部分和以下部分构件的长度分别为L1和L2，则该构件的几何尺寸满足下式

L=L1+Lmd+L2

(1)

A=Amd+As

(2)

在轴向压力F的作用下，设装有磁流变阻尼器部分构件的变形为Δmd，磁流变阻尼器以上部分构件和以下部分构件的变形分别为Δ1和Δ2，构件的总变形为Δ，则构件变形满足下式

Δ=Δ1+Δmd+Δ2

(3)

根据材料力学基本原理[9]，可得

(4)

(5)

(6)

(7)

(8)

(9)

将式(8)和式(9)代入式(7)，可得:

(10)

将式(1)～式(6)代入式(10)，可得:

(11)

将式(11)整理，可得:

(12)

式(12)可用于计算装有磁流变阻尼器的构件的整体弹性模量，定义αE为整体弹性模量系数，则

(13)

(14)

(15)

因此，式(13)可以改写为

(16)

2 受压构件刚度折减试验研究

2.1 试验介绍

本试验利用输电塔空间桁架截断模型，模拟其在承受动力荷载作用过程中，某关键受压构件发生瞬时刚度折减，通过对相关物理量的实时采集，结合信号处理方法，判定发生刚度折减的损伤时间。该模型系角钢输电塔结构底部两层的截断模型，在模型顶部增加配重以模拟截断部分以上的质量。该模型整体为格构式结构，各构件主要承受轴心压力作用。因此可以使用本文提出的方法进行损伤模拟,试验模型及数据采集系统如图3所示。

图3 试验模型及数据采集系统

该试验采用的加载装置为江苏联能公司生产的JZK-20型激振器及配套的功率放大器、信号发生器。通过调节信号发生器，可使激振器产生幅值为20 kgf的正弦信号、白噪声信号等。激振器通过自制的活动支架固定在反力墙上，在每个激振器触头前安装力传感器后与结构固定。激振器、力传感器的安装如图4所示。

图4 激振器及力传感器

2.2 磁流变阻尼器的安装

将桁架模型的一根主要受压杆件，按照磁流变阻尼器的长度截断，在截断端头部分焊接栓孔，再将磁流变阻尼器通过该栓孔与构件相连。安装时使磁流变阻尼器的中心通过该杆件截面中心。磁流变阻尼器的安装如图5所示。

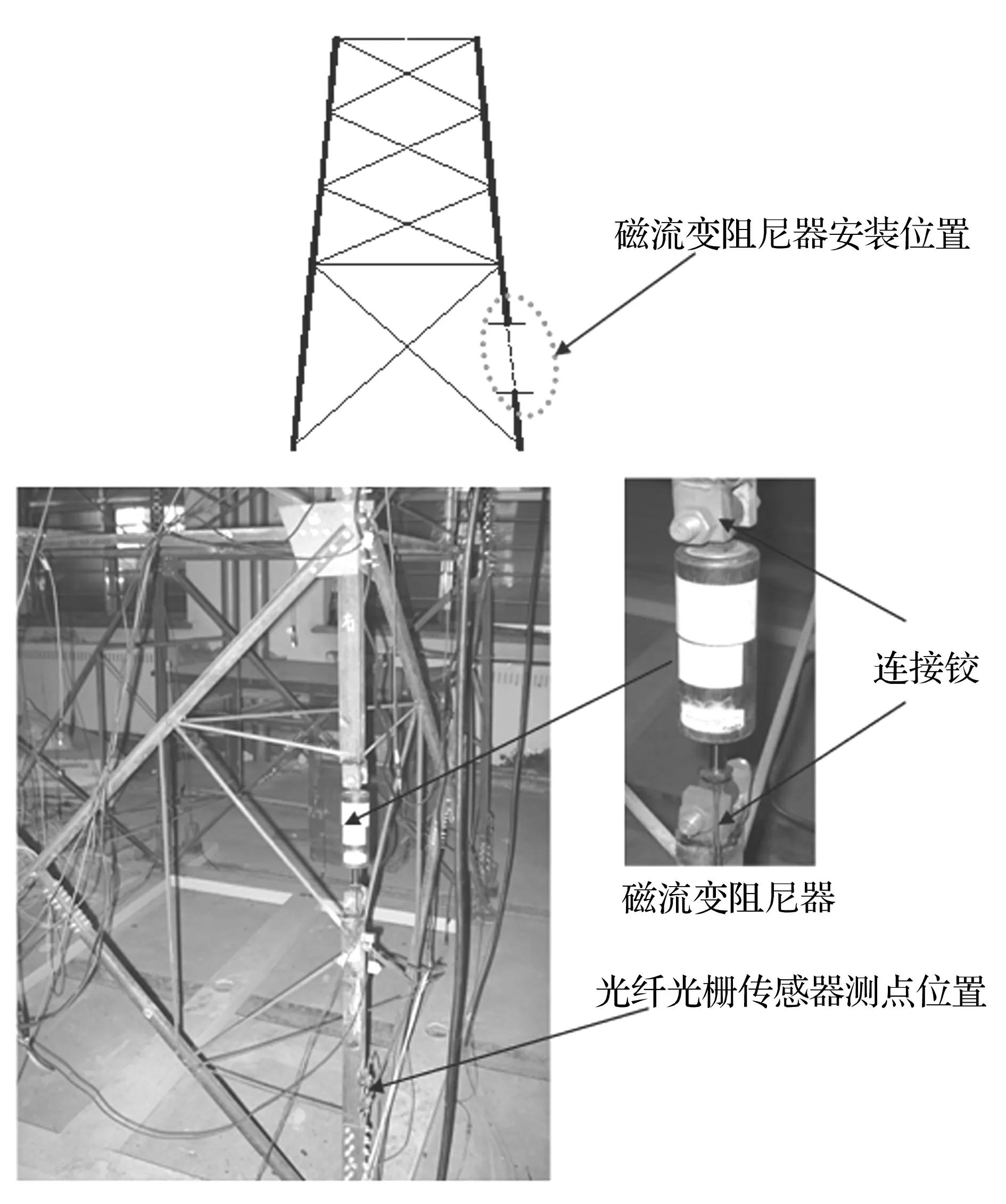
图5 磁流变阻尼器的安装

2.3 传感器及数据采集

对于轴心受压构件，其应力或应变是反应其健康状况的最直接的参数。本试验采用光纤光栅应变传感器，对上述装有磁流变阻尼器的受压构件进行应变监测。光纤光栅传感器具有灵敏度高，抗电磁干扰等优点[10-11]。在角钢表面焊接传感器支座，并将传感器通过螺栓连接固定在支座上，这种方式不破坏原结果，且确保了光纤光栅传感器与结构的一致变形。为了验证该试验方法，在磁流变阻尼器所在的模型平面布置了5个光纤光栅应变传感器，测试该构件在损伤模拟过程中的动态应变响应。其中，B1、B2、B3三个传感器用于测量竖杆(对应输电塔模型主材)的应变，H1用于测量横杆(对应输电塔模型横材)的应变，X1用于测量斜杆(对应输电塔模型斜材)的应变。光纤光栅传感器的安装方法及测点布置如图6、7所示。此外还布设了一个光纤光栅传感器以进行温度补偿。但由于结构损伤是一种瞬态变化，温度变化频率较低，损伤信号的影响并不明显。

图6 光纤光栅传感器安装方法

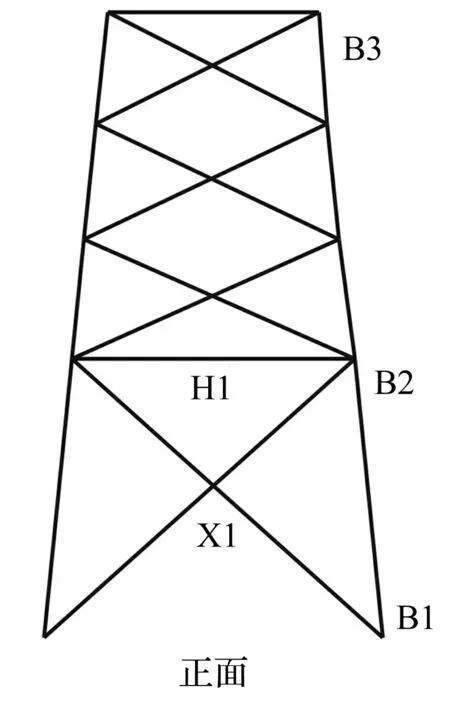
图7 光纤光栅传感器测点位置

光纤光栅传感器的数据采集系统为美国MOI公司生产的光纤光栅解调仪SM230，它可以同时解调16个通道的光信号，每个通道可以串接多个传感器，实现结构的多点测量。采样频率可达到250 Hz，能够满足土木结构动态测量的要求。

2.4 加载及损伤模拟

为获得较大的响应信号，首先利用激振器对结构进行白噪声扫频，获得结构的基频，约为15.4 Hz。然后将激振器的信号发生器调频至15 Hz，输出正弦波，便可获得较大的结构响应。在结构加载过程中，利用磁流变阻尼器的电流控制器，调节通电电流，即可改变构件抗压刚度，模拟构件刚度突变。每次试验加载时间约为40 s，在第20 s附近调节电流控制器，使构件发生刚度折减。加载过程中，实时采集各个传感器的应变响应数据，而后对该数据进行分析，判定损伤时间。

3 试验数据及分析

3.1 原始应变响应时程

图8列出了加载过程中采集的各个光纤光栅传感器的原始应变时程数据,为便于观察，截取了加载过程中20 s附近的时程。对于传感器B1、B2所在测点，由于距离磁流变阻尼器较近，其在磁流变阻尼器电流调整前后，可以看出由于刚度突变造成的应变幅值发生变化。在B1、B2两个时程曲线中，可以粗略判断应变幅值发生改变的时间接近20 s末，但仍无法判断损伤发生的具体时间。

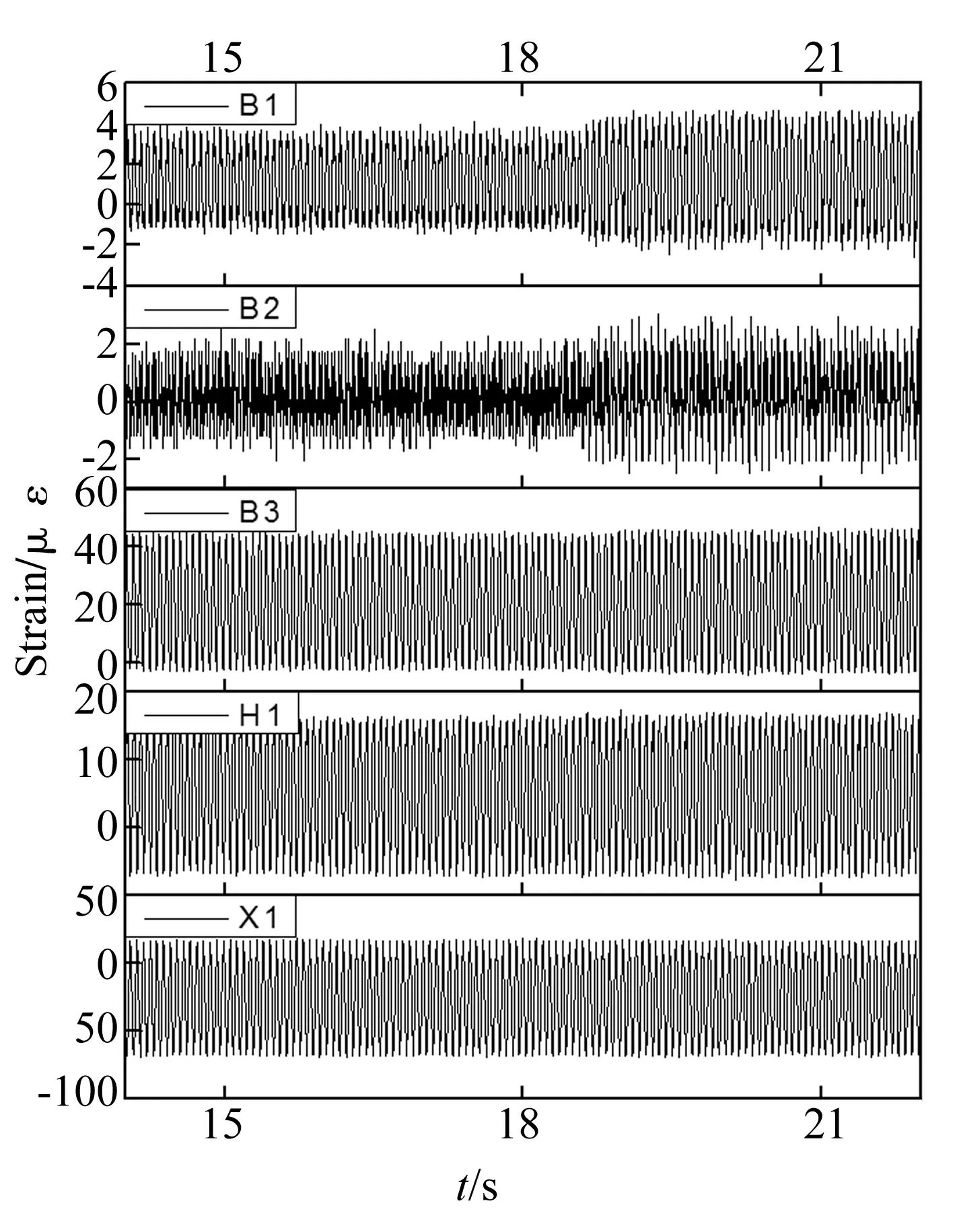
图8 光纤光栅传感器应变响应时程

而对于B3、H1、X1三个应变测点，由于距离磁流变阻尼器较远，在结构动态加载过程中，对该位置的损伤极不敏感，根据这三条曲线已经无法分别出刚度折减前后应变响应幅值的变化并判别损伤发生的时间。

3.2 基于短时傅里叶变换的损伤识别

3.2.1 短时傅里叶变换

在传统的信号处理中，傅里叶变换构架起了信号时域和频域的桥梁。然而傅里叶变换只是一种信号的整体变换，只能了解信号在时域或者频域的全局特性，并不能表达有关频率成分的时间局部化信息。为了弥补傅里叶分析这一不足,针对非平稳信号, 引出了时频分析方法[12-14]。

短时傅里叶变换(STFT，short-time Fourier transform)属于线性时频分析中的一种[12,15-16]，其本质是加窗傅里叶变换：用窗函数去截取原始时域信号，对截取的局部信号作傅里叶变换，即得到在t时刻该段信号的频谱分布。不断地移动t，即不断移动窗函数的中心位置，即可得到不同时刻的频谱分布，而这些傅里叶变换的合集即是短时傅里叶变换。

当结构发生损伤，其频率和刚度会发生改变，在结构响应中会出现不连续的奇异点。利用短时傅里叶变换，可以根据频率随时间的变化，判别损伤发生的时间。

3.2.2 基于短时傅里叶变换的损伤时间定位

短时傅里叶变换的程序代码基于LabView软件平台编写，利用STFT Spectrogram模块实现短时傅里叶变换，进而分析信号在时-频平面上的能量分布情况。图9(a)～图9(c)分别给出了传感器B1的应变响应时程曲线，短时傅里叶变换的能量分布，以及16Hz频率成分的能量密度随时间的变化关系。在短时傅里叶变换中，滑动窗口的采样点数为32，频率区间为默认的512 Hz，窗函数类型选用汉宁窗。从能量分布图9(b)可以看出，构件发生损伤前后，即调节磁流变阻尼器通电电流前后，结构应变响应的频率成分发生了明显的变化。损伤发生后，在14～16 Hz范围内，能量显著增大，据此可以判断结构发生损伤。单独提取16 Hz的频率成分，如图9(c)，考察该频率成分在时域上的变化。从中可以看出，该频率成分的能量在损伤前后发生突变，从该信号的拐点，即可准确判别出损伤发生的时间，为18.4 s。

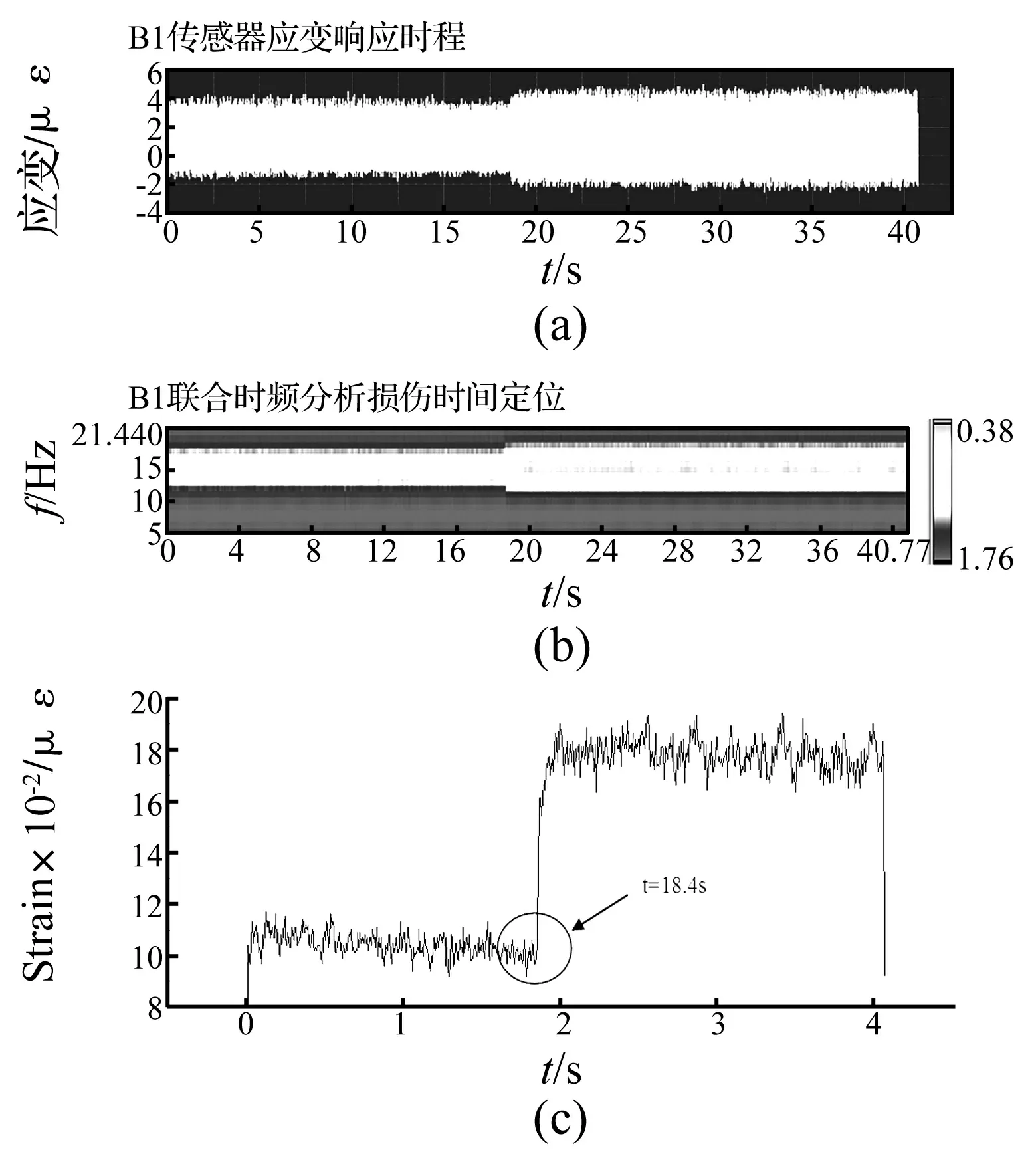
图9 B1应变响应时程曲线及短时傅里叶变换

对B1、B2、B3、H1、X1等全部传感器的应变响应数据分别做短时傅里叶变换，并提取16Hz的频率成分，如图10所示。可以看出，B1、B2、B3测点的该频率成分的能量变化曲线可以清晰的分辨出信号突变点，用来准确判断结构发生损伤的时间。而H1、X1测点由于距离刚度折减位置较远，单纯由其应变响应时程信号(图8)已无法分辨出结构是否发生损伤。而从图10中H1、X1测点的短时傅里叶变换结果，则能够看出16 Hz频率成分的能量变化，据此也可以粗略判断损伤发生的时间。总体来看，各应变响应信号的短时傅里叶变换结果趋势基本一致，均可用于确定结构损伤时间。

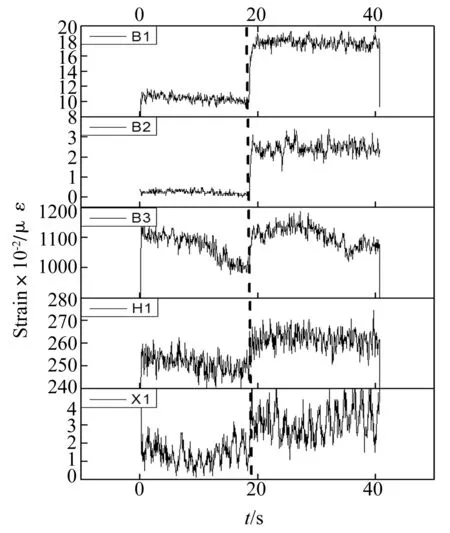
图10 各传感器16 Hz频率成分的能量随时间的变化

4 结 论

本文提出了一种利用磁流变阻尼器模拟受压构件刚度折减的试验方法，并对其进行了试验验证。在结构动力加载过程中，调整磁流变阻尼器的通电电流，来模拟受压构件的刚度瞬时折减。结合短时傅里叶变换的方法，对损伤时间进行定位。根据试验结果可以得出以下结论：

(1) 调整磁流变阻尼器的通电电流，可以改变其弹性模量，进而改变构件的整体抗压刚度。

(2) 磁流变阻尼器具有响应快的特点，可用于模拟结构动力加载过程中的刚度瞬时折减，并准确控制构件的损伤时间。

(3) 原始时域信号经过短时傅里叶变换，能够准确判断结构发生损伤的时间。

(4) 根据试验要求，设计磁流变阻尼器的长度及截面面积，即可改变构件的整体弹性模量系数αE对于通电电流i的灵敏度。此问题有待后续试验研究。

参 考 文 献

[1]陆秋海，李德葆，张维. 利用模态试验参数识别结构损伤的神经网络法[J].工程力学，1999,16(1):1-8.

LU Qiu-hai, LI De-bao, ZHANG Wei. Using modal test parameter identification structure damage nerve network[J]. Journal of Engineering mechanics, 1999,16(1):1-8.

[2]王兴国，李华军，潘新颖. 小波包分析在结构损伤时间识别及结构模态参数识别中的应用[J].工程力学(增)，2003：1-8.

WANG Xing-guo, LI Hua-jun, PAN Xin-ying. Wavelet packet analysis in structural damage time identification and structure of the application of modal parameter identification[J]. Journal of Engineering mechanics, 2003,(S)：1-8.

[3]陈淮，李静斌，殷学刚. 一种新的结构损伤识别试验方法研究[J].实验力学，2011,26(1)：1-7.

CHEN Hui, LI Jing-bin, YIN Xue-gang. A new kind of structural damage identification test method[J]. Journal of Experimental mechanics, 2011, 26(1)：1-7.

[4]王鸿云，郑惠强，李泳鲜. 基于挤压模式下磁流变液力学行为的实验研究[J].仪器仪表学报，2009,30(4)：1-4.

WANG Hong-yun, ZHENG Hui-qiang, LI Yong-xian. Based on the squeeze mode magnetorheological fluid learning behavior of the experimental study [J].Instrument Journal，2009,30(4)：1-4.

[5]方子帆，邓兆祥. 磁流变阻尼器简化力学模型研究[J].工程力学，2007,24(11):1-5.

FANG Zi-fan, DENG Zhao-xiang. Model of magnetorheological damper study [J]. Journal of Engineering mechanics,2007,24(11):1-5.

[6]曹磊. 磁流变液阻尼器力学性能研究与应用[D].宁波：宁波大学，2009.

[7]王鸿云，高春浦，阚君武，等. 场作用下磁流变液的挤压与拉伸特性[J].光学精密工程，2011,19(4):1-7.

WANG Hong-yun, HONG Chun-pu, HAN Jun-wu, et al. Field under the action of MRF squeeze and tensile characteristics [J].Journal of Optical precision engineering , 2011,19(4):1-7.

[8]Mazlan S A, Ekreem N B, Olabi A G. An investigation of the behaviour of magnetorheological fluids in compression mode[J]. Journal of Materials Processing Technology, 2008, 201(1-3):780-785.

[9]孙训芳，方孝淑，关来泰. 材料力学[M]. 第5版, 北京:高等教育出版社,2009.

[10]李宏男，任亮. 结构健康监测光纤光栅传感技术[M]. 第一版，北京：中国建筑工业出版社，2008.

[11]JIA Zi-guang, REN Liang, LI Dong-sheng. Design and application of the ice force sensor based on fiber Bragg grating[J]. Measurements, 2011, 44(10): 2090-2095.

[12]臧观建，刘正平. 基于LABVIEW的联合时频分析[J]. 华东交通大学学报，2007, 24(4)：1-4.

ZANG Guan-jian, LIU Zheng-ping. Based on LABVIEW joint time-frequency analysis [J]. Journal of east China Jiaotong University, 2007,24(4)：1-4.

[13]石志晓，李昕，周晶. 时频联合分析方法在土木工程中的研究现状[J].工业建筑，2005, 35(5):1-7.

SHI Zhi-xiao, LI Xi, ZHOU Jing. Time-frequency joint analysis method in civil engineering research status of [J].Journal of Industrial Buildings, 2005,35(5):1-7.

[14]石岩，常思勤. 基于STFT谱的声强短时傅里叶变换仪器仪表学报[J].仪器仪表学报，2009, 29(4):1-6.

SHI Yan,CHANG Si-qin. Based on STFT spectrum of sound intensity joint time-frequency analysis[J]. Instrument journal, 2009,29(4):1-6.

[15]Bonato P, Ceravolo R, De Stefano A. Time-Frequency and Ambiguity Function Approaches in Structural Identification[J]. Journal of Engineering Mechanics, 1997, 123: 1260-1267.

[16]QIAN Shi-e, CHEN Da-peng. Joint time-frequency analysis[J]. IEEE Signal Processing Magazine, 1999,16(2):53-67.