穿孔管阻性消声器横向模态和声学特性计算与分析
2014-09-05季振林
方 智, 季振林
(哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
穿孔管阻性消声器具有较宽的消声频率范围(尤其在中高频段)和较低的流动阻力损失,在管道噪声控制中被广泛使用。数值方法[1-4]和解析方法[5-8]均被应用于研究此类消声器的声学特性。数值方法可以计算任意形状横截面的消声器的消声特性,但是对消声器的尺寸和计算机的要求较高,一般需要的计算时间较长。解析方法所需的计算时间短,并且精度较高,但是只能计算横截面形状规则的消声器(如圆形横截面和矩形横截面)。解析方法的另一个缺点在于它求解膨胀腔的横向波数时需要解特性方程,无论采用正割线法[5-7]还是牛顿法[8-9]均容易产生丢根现象,并且需要的时间较长。为了同时避免数值方法和解析方法的缺点,本文使用数值模态匹配法求解任意形状横截面穿孔管阻性消声器的传递损失。数值模态匹配法的基本思想为:应用二维有限元法求解消声器管道和腔内的横向模态,提取出本征波数和本征向量,进而得到消声器横截面的本征函数;利用模态匹配技术建立消声器内声压和轴向质点振速的解析表达式,结合边界条件和连续性条件以及本征函数的正交性,求出模态幅值系数,进而得到消声器的传递损失。数值模态匹配法解决了解析方法丢根的困扰和对横截面形状的限制问题,由于只需要对横截面划分二维网格,因而所需要的时间也大为减少,并且能够根据求出的本征模态分析高阶模态的影响和平面波理论的适用范围,具有明显的优点。本文研究的目的在于:① 应用二维有限元法求解直通穿孔管阻性消声器的横向模态,利用模态匹配技术计算消声器的传递损失;② 分别应用数值模态匹配法、三维有限元法以及实验测量得到圆形同轴穿孔管阻性消声器的传递损失,通过比较验证本文数值模态匹配法的正确性;(3)分析孔径、穿孔率、吸声材料密度和穿孔管偏移对直通穿孔管阻性消声器横向模态和消声特性的影响。
1 横向模态求解的有限元法
图1为任意形状等截面直通穿孔管阻性消声器示意图,将其分为三个区域:进口管A、膨胀腔C和出口管E,对应的横截面分别为S1、S3=S1+S2和S1。膨胀腔被穿孔管分为两部分:C1和C2,对应的横截面分别为S1和S2,C2内填充吸声材料。

图1 任意形状等截面直通穿孔管阻性消声器
以膨胀腔C为例,介绍数值模态匹配法的基本思想。C1和C2内简谐声场的控制方程为[10]
2p1(x,y,z)+k2p1(x,y,z)=0
(1)
(1)
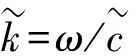
消声器的边界条件可分成如下两类。
(a) 刚性壁面边界条件可以表示为
∂p2/∂n=0
(3)
(b) 穿孔表面边界条件可以表示为[10]
(4)

(5)

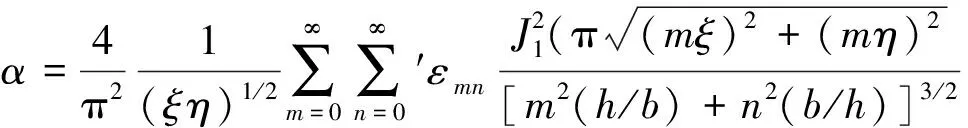

利用欧拉方程,穿孔表面法向声压梯度表达式为
∂p1/∂n=-jρ0ωun
(7)
(8)

结合方程(4)和(7) 可以得到
(9)
结合方程 (4) 和 (8) 可以得到
(10)
方程(1)和(2)的解可以写成[13]
(11)
式中pxy为横向声压分量,i代表模态阶数,A和B分别为沿z轴正反方向的模态幅值系数,kz为轴向波数。横向声压pxy满足以下方程[13]:
(12)
(13)

(14)
(15)
将表达式(11)代入边界条件(3),(9)和(10)中得到
(16)
(17)
(18)
对于任意形状的横截面,方程(12)和(13)需要使用数值方法,例如二维有限元法[14]。
在横截面S1内, 将加权残数法和格林方程以及边界条件应用于方程(12)得到
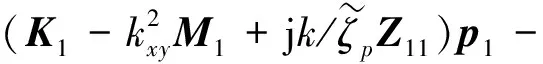
(19)
式中,

分别为对应于横截面S1的广义刚度矩阵、质量矩阵和穿孔阻抗矩阵,下脚标 “e”代表单元。
相似地,在横截面S2内有
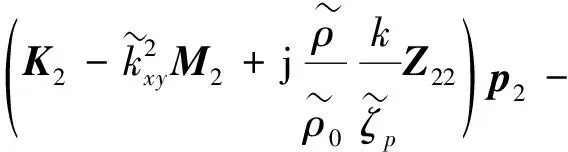
(20)
式中,K2,M2以及Z2分别为横截面S2的广义刚度矩阵、质量矩阵和穿孔阻抗矩阵。N为广义形函数的列向量,p1和p2分别为横截面S1和S2上节点声压组成的列向量。
结合式 (19)和式(20)得到:
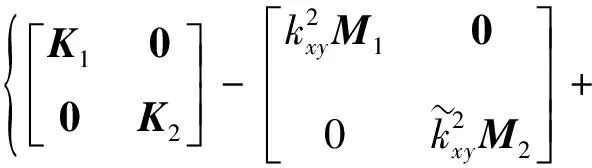
(21)
为了方便地求解方程(21),引入轴向波数,得到如下方程
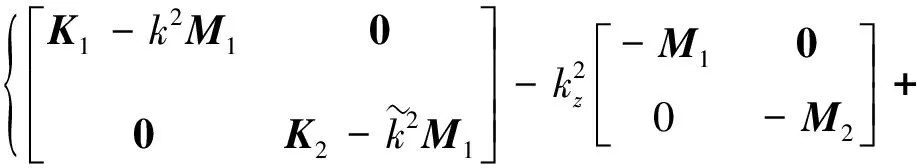
(22)
求解方程(22)可以得到膨胀腔内的轴向波数和对应的本征向量。
对于进出口管道的横截面,由于不含有穿孔表面,所以表达式(22)可以简化为
(23)
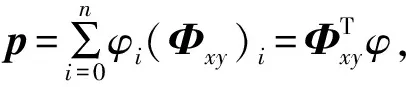
消声器内的横向声压分量可以表示为
(24)
式中φi和(Φxy)i分别代表第i阶模态的幅值系数和横向本征向量。
于是,声压可以改写成
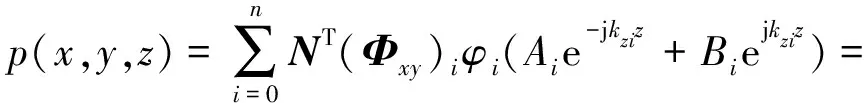
(25)
式中Ψi(x,y)=NT(Φxy)i为本征函数。
2 模态匹配法
结合进出口所在截面的连续性条件和边界条件,利用本征函数的正交性,建立模态幅值系数之间的关系,进而可求出穿孔管消声器的传递损失。
考虑如图1所示的消声器,每个区域内的声压和轴向质点振速可以表示成如下形式。
在区域A,E内(I=A,E):
(26)
(27)
式中,在区域A内z′=z,在区域E内z′=z-L。
在区域C内:
(28)
UC,z=
(29)
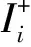
进出口横截面上的声压和轴向质点振速的连续性条件和边界条件可以表示为,
PC(z=0)=PA(z=0),(x,y)∈S1
(30)
(31)
PC(z=L)=PE(z=L),(x,y)∈S1
(32)
(33)
在进出口横截面上,将声压和质点振速表达式代入到连续性条件和边界条件式(30)-式(33)中,并且在方程两边同时乘以相应积分面上的本征函数并积分,得到

(34)
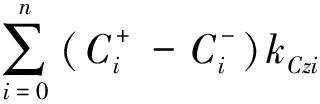
(35)

(36)
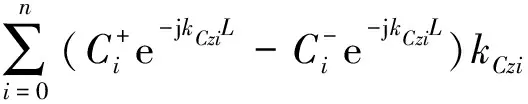
(37)
式中,
ΨCiΨCjS3=ΨCiΨCjS2
利用本征函数的正交性有,
ΨiΨjΨiΨj
(38)

(39)
3 算例及分析
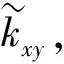
为了验证本文方法和编写的计算程序的正确性,首先应用数值模态匹配法计算如图2所示的圆形同轴直通穿孔管阻性消声器(δ=0)的传递损失,并与三维有限元法计算结果以及实验测量结果进行比较。消声器的具体尺寸为:膨胀腔直径和长度分别为d=164.4 mm,L=257.2 mm,进出口管道直径为d=49 mm,穿孔管壁厚为tw=0.9 mm,声速取344 m/s,δ为进出口的偏移量。吸声材料为玻璃丝绵,其特性声阻抗和复波数的表达式为[11]:
密度为100 g/L:
(40)
(41)
密度为200 g/L:
(42)
(43)
式中,z0=ρ0c0为空气的特性声阻抗。在以下的分析以及3.1节,3.2节和3.4节的分析中,吸声材料的密度均为100 g/L。
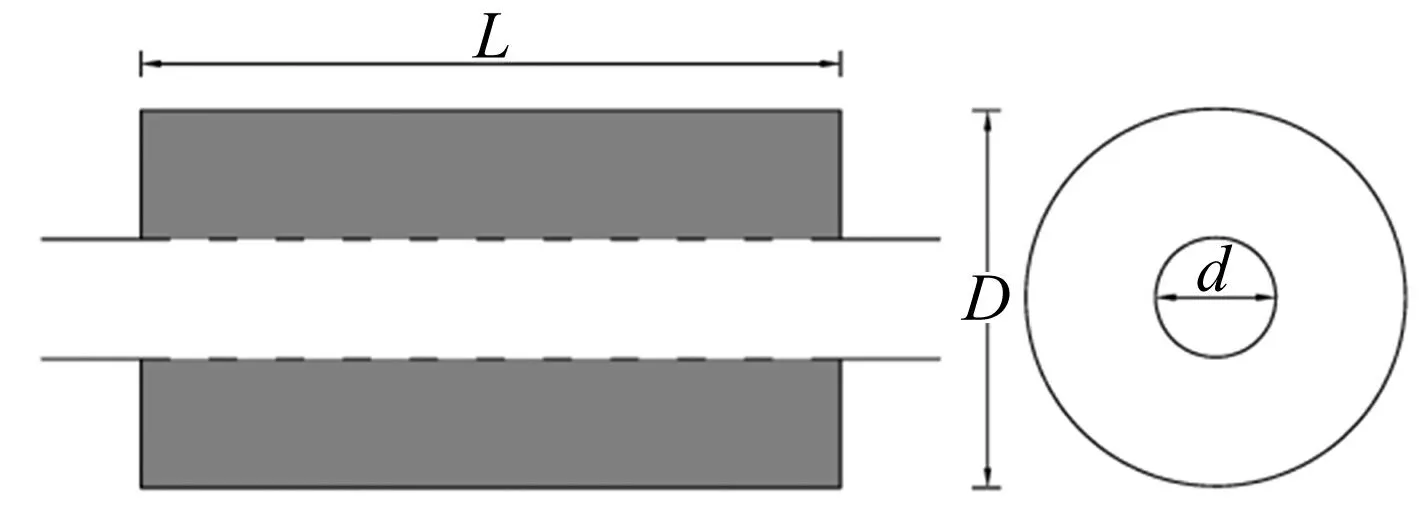
图2 圆形同轴直通穿孔管阻性消声器
图3为取不同模态数时圆形同轴直通穿孔管阻性消声器的传递损失计算结果比较,其中穿孔率为φ=8.4%,孔径为dh=2.49 mm。由于消声器为轴对称结构,只有径向模态能被激发,图3中给出的是径向模态数,为了与下文模态数N区分,这里用Nr表示径向模态的阶数。为估算在所计算的频率范围内消声器能激发的横向模态阶数,根据计算的最高频率3 200 Hz估算出最大的横向波数为k=2πf/c=58.42。激发频率为3 200 Hz时,消声器的第1阶径向模态对应的Re(kxy)为36.18,第二阶径向模态对应的Re(kxy)为63.10,由此可以粗略判断在3 200 Hz以内只有第一阶径向模态为可传播的模态;第二阶径向模态不可传播(为耗散模态),对消声器的声学特性影响较小。从传递损失曲线上也可以看出,取前两阶径向模态和前三阶径向模态时传递损失曲线完全重合,所以在所关心的频率范围内,计算此结构消声器的传递损失取前两阶径向模态即可保证计算精度。相似地,下文中消声器取不同孔径和穿孔率以及不同的填充密度时,模态阶数对计算精度的影响分析与此相似,由分析结果得到计算本文同轴穿孔管阻性消声器时取前两阶径向模态均可保证计算精度,所以在本文计算中,所有同轴消声器的传递损失曲线中均取Nr=2。
图3中Nr=0表示没有考虑高阶模态的影响,即一维平面波计算结果。一维平面波理论只有在平面波区域即消声器的平面波截止频率以下适用,高于截止频率,一维结果与三维结果出现偏差。由此可以大致地判定一维平面波理论的适用范围。

图3 模态阶数对圆形同轴直通穿孔管阻性消声器传递损失的影响
图4给出了使用数值模态匹配法和三维有限元法计算得到的消声器传递损失和实验测量结果[15]的比较。实验测量结果是应用两负载方法在B&K阻抗管测量装置上测量得到。测量过程中声源位置不动,改变出口的边界条件。声源由阻抗管套件中的信号发生器模块产生,出口的两个边界条件分别通过在出口处安装吸声材料和完全开口来获得。可以看出,数值模态匹配法计算结果与有限元法计算结果在整个频段内吻合很好,两种方法计算结果与实验测量结果在高频段产生偏差。产生偏差的原因有可能是吸声材料填充不够均匀,穿孔阻抗公式和吸声材料的等效表达式在高频不够精确所致。良好的吻合证明了数值模态匹配法计算穿孔管阻性消声器声学特性的正确性。
为了进一步验证数值模态匹配法的适用性和正确性,图5比较了方形截面结构消声器的传递损失结果。消声器的尺寸与图2中圆形截面结构消声器的尺寸相同,横截面面积相等。图5中数值模态匹配法计算结果与有限元结果吻合较好,从而进一步验证了数值模态匹配法的适用性和正确性。
3.1 孔径的影响
图6为应用数值模态匹配法计算得到的两种孔径下直通穿孔管阻性消声器的传递损失。可以看出,孔径较小的消声器高频消声量高于孔径大的消声器,而在中频的消声量略低于孔径大的消声器,孔径对消声器低频的消声效果几乎没有影响。

图6 不同孔径直通穿孔管阻性消声器传递损失比较
表1给出了穿孔率为8.4%,孔径分别为2.49 mm和4.98 mm时消声器横截面的前两阶径向模态的形状和对应的Re(kxy)。可以看出,孔径越大,相同阶次的模态对应的横向波数的实部数值越小,说明第一阶径向模态越早被激发,消声器内三维波出现的越早,即消声器的平面波区域越窄。

表1 不同孔径穿孔管阻性消声器横向模态比较
图7给出了穿孔率为8.4%时,孔径分别为0.62 mm、1.25 mm、2.49 mm、3.74 mm、4.98 m、7.47 mm和9.96 mm几种情况下计算得到的第一阶模态对应的横向波数的实部数值Re(kxy)。可以看出,在同样穿孔率下,孔径越大,第一阶模态对应的Re(kxy)越小。
图8则比较了应用数值模态匹配法计算得到的不同孔径时直通穿孔管阻性消声器的传递损失结果。可以看出,孔径增大,传递损失曲线中的峰值向低频方向移动,高频消声效果变差,而中频消声效果变好。
3.2 穿孔率的影响
图9比较了孔径为2.49 mm,穿孔率分别为2.1%和8.4%时直通穿孔管阻性消声器的传递损失。可以看出,穿孔率为2.1%的直通穿孔管消声器在中低频出现了共振峰,消声特性较好,但是,在高频的消声量则远远低于穿孔率为8.4%的消声器。
表2给出了孔径为2.49 mm,穿孔率分别为2.1%和8.4%时前两阶径向模态形状以及对应的Re(kxy)。可以看出,穿孔率增大,相同阶次模态对应的横向波数的实部数值 增大,因而消声器的平面波截止频率升高。

表2 不同穿孔率穿孔管阻性消声器横向模态比较
图10给出了孔径为2.49 mm时,穿孔率分别为2.1%、4.2%、8.4%、16.8%、25.7%、40%以及穿孔率为100%的极限状况时计算得到的第一阶模态对应的横向波数的实部数值Re(kxy)。可以看出,在同一孔径下,穿孔率越大,第一阶模态对应的Re(kxy)越大,穿孔率大于40%以后穿孔率对第一阶模态对应的Re(kxy)的影响较小。
图11为应用数值模态匹配法计算得到的不同穿孔率时直通穿孔管阻性消声器的传递损失。可以看出,穿孔率升高,传递损失曲线中的峰值向高频移动,消声器中低频的消声量降低,高频的消声量升高,穿孔率大于40%以后,穿孔率对传递损失的影响很小,尤其是在中低频,传递损失曲线几乎重合。
图9 不同穿孔率直通穿孔管阻性消声器传递损失比较
3.3 吸声材料密度的影响
图12比较了不同吸声材料密度下消声器的传递损失。可以看出,在250 Hz以下,吸声材料对消声器的声学特性几乎没有影响,这是因为吸声材料对低频声波的吸声能力较弱,消声器主要以抗性衰减为主。高于250 Hz,吸声材料填充密度大的消声器的消声量远高于填充密度小的消声器。填充密度越大,传递损失曲线中峰值频率越低,整体消声效果越好。

图12 吸声材料密度对穿孔管阻性消声器消声特性的影响
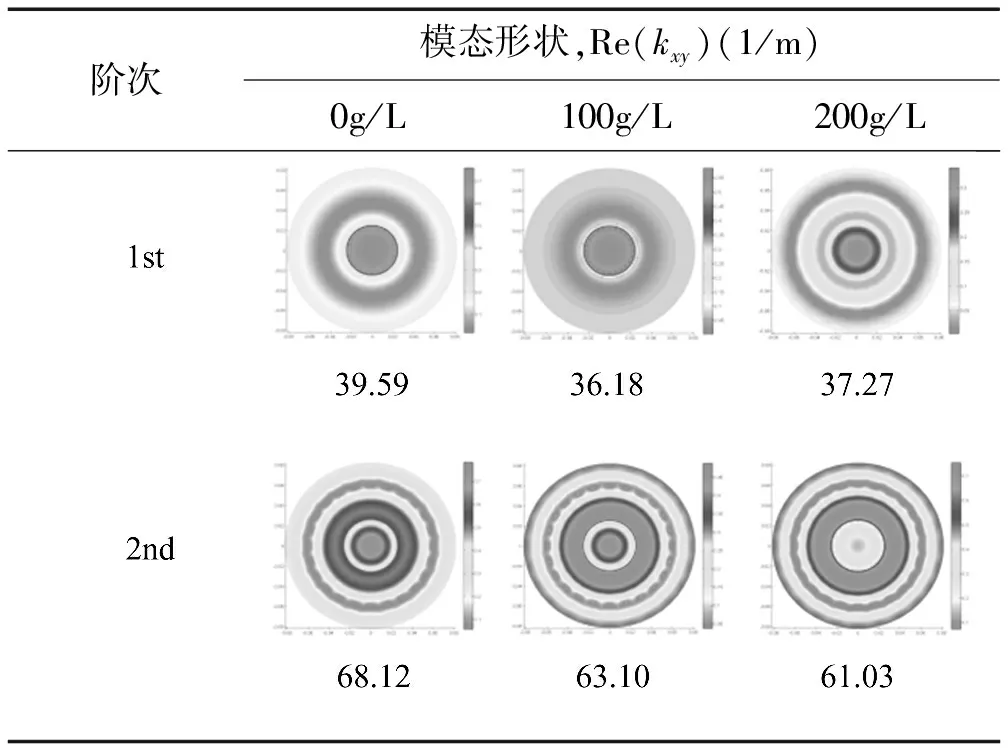
表3 吸声材料密度对穿孔管阻性消声器横向模态的影响
表3给出了有无吸声材料填充时消声器的横向模态。对于抗性消声器(填充密度为0),声波主要是通过来回反射被衰减掉,中低频消声特性与简单膨胀腔相似。对于阻性消声器,声波引起吸声材料的振动,将声能转换成热能而被衰减掉。吸声材料密度越大,消声器内第一阶径向模态对应的Re(kxy)越大,消声器有效的平面波区域越宽。
3.4 穿孔管偏移的影响
由于安装空间的限制,非同轴穿孔管阻性消声器(如图13所示)在工程中也被广泛使用,由于数值模态匹配法不受几何形状的限制,因而可用于计算这类消声器的横向模态和传递损失,从而为工程设计提供有实用价值的分析方法。
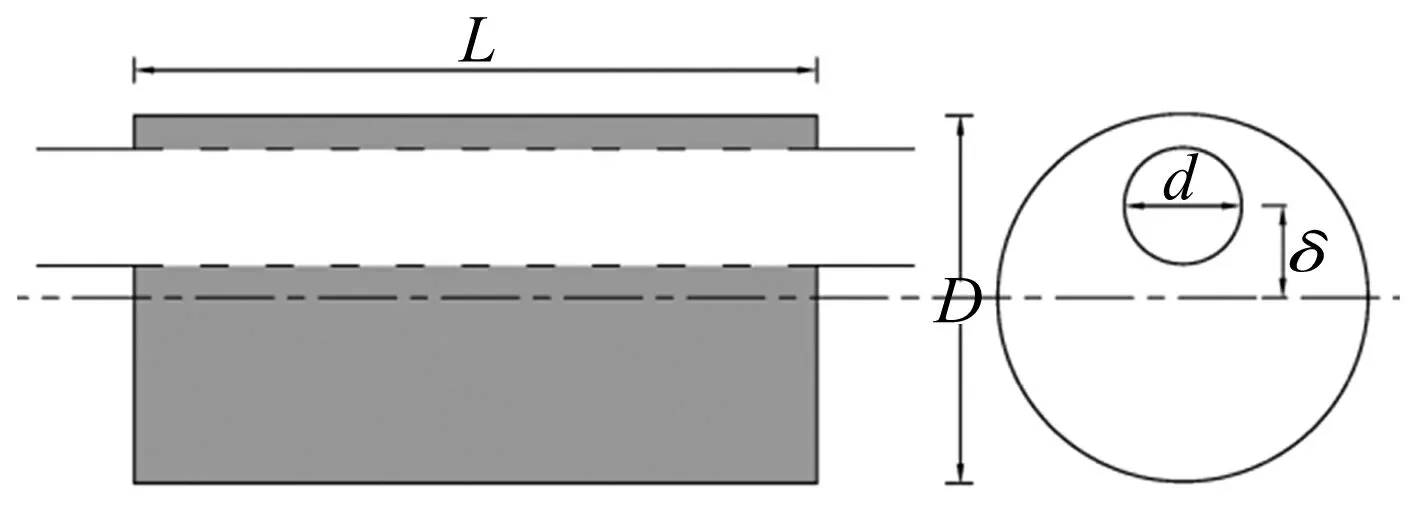
图13 圆形非同轴直通穿孔管阻性消声器
为了确定计算穿孔管偏移的阻性消声器的传递损失时需要的模态阶数,图14和图15分别给出了δ=25 mm和δ=50 mm的消声器在取不同模态阶数时的传递损失。与同轴结构的分析相似,对于穿孔管偏移25 mm的消声器,第8阶高阶模态对应的Re(kxy)为47.08,而第9阶高阶模态对应的Re(kxy)为58.42,说明在3 200 Hz范围内,前8阶高阶模态是可传播的模态,而第9阶以后的模态为耗散模态,对消声器的声学特性的影响随着模态阶次的升高逐渐变小。图14中,取N=13与N=14时得到的传递损失曲线完全吻合,说明在3 200 Hz范围内第13阶以上的高阶模态对消声器传递损失的影响可以忽略不计,所以在3 200 Hz范围内取N=13可以保证计算精度。同理,对于穿孔管偏移50 mm的消声器,计算传递损失时取前13阶模态即可。
图16比较了穿孔管偏移对消声器传递损失的影响,同时也比较了数值模态匹配法计算结果与有限元结果。两种计算结果的吻合验证了数值模态匹配法计算穿孔管偏移阻性消声器声学特性的正确性。穿孔管的偏移量对消声器消声性能的影响与频率相关。在低频区域,穿孔管的偏移对消声器的消声量几乎没有影响;而在中频区域,偏移量越大,消声器的消声效果越差;在高频偏移量最大的消声器则展现出最好的消声效果。

图14 模态阶数对不同轴穿孔管阻性消声器(δ=25 mm)传递损失的影响
表4比较了穿孔率为8.4%,孔径为2.49 mm,穿孔管分别偏移δ=0,δ=25 mm和δ=50 mm时穿孔管消声器的前三阶横向模态。由于同轴消声器只能激发径向模态(第三阶高阶模态),所以同轴结构的平面波截止频率高于穿孔管偏移结构的消声器。

表4 穿孔管偏移对穿孔管阻性消声器横向模态的影响
4 结 论
应用二维有限元方法求解任意形状横截面的直通穿孔管阻性消声器的横向模态,利用数值模态匹配技术求解消声器的模态幅值系数,进而计算得到消声器的传递损失。对于圆形同轴穿孔管阻性消声器的传递损失,数值模态匹配法计算结果与三维有限元法计算结果以及实验测量结果吻合良好,从而验证了本文数值模态匹配法计算穿孔管阻性消声器消声特性的准确性。进而应用数值模态匹配法计算并分析了穿孔孔径、穿孔率、吸声材料密度和穿孔管偏移对圆形直通穿孔管阻性消声器消声特性和横向模态的影响。计算结果表明,孔径、穿孔率、吸声材料密度和穿孔管偏移对消声器声学特性的影响是与频率相关的;孔径越大,消声器的平面波有效范围越窄,中频消声效果越好,消声器高频消声效果越差;穿孔率越高,消声器的平面波截止频率越高,中频消声量越低,而高频消声量越高。穿孔率高于40%,穿孔率对消声器的声学特性影响较小,尤其在中低频。吸声材料的密度越高,消声器中高频的消声效果越好。穿孔管的偏移量在不同的频段内对消声器的消声效果影响不同。
参 考 文 献
[1]Peat K S,Rathi K L. A finite element analysis of the convected acoustic wave motion in dissipative silencers [J]. Journal of Sound and Vibration, 1995, 184(3): 529-545.
[2]Selamet A,Lee I J, Huff N T. Acoustic attenuation of hybird silencers [J]. Journal of Sound and Vibration, 2003, 262: 509-527.
[3]Ji Z L, Boundary element analysis of a straight-through hybird silencer [J]. Journal of Sound and Vibration, 2006, 292: 415-423.
[4]Ji Z L, Boundary element acoustic analysis of bybird expansion chamber silencers with perforated facing [J]. Engineering analysis with boundary element, 2010, 34: 690-696.
[5]Selamet A, Xu M B, Lee I J. Analytical approach for sound attenuation in perforated dissipative silencers. [J]. Journal of Acoustical Society of America. 2004, 115(5):2091-2099.
[6]Selamet A, Xu M B, Lee I J. Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extension [J]. Journal of Acoustical Society of America. 2005, 117(4):2078-2089.
[7]Denia F D, Selamet A, Fuenmayor F J, et al. Acoustic attenaution performance of perforated dissipative mufflers with empty inlet/outlet extensions [J]. Journal of Sound and Vibration, 2007, 302: 1000-1017.
[8]Kirby R. Simplified techniques for predicting the transmission loss of a circular dissipative silencer [J]. Journal of Sound and Vibration, 2001, 243: 403-426.
[9]Kirby R, Denia F D. Analytic mode matching for a circular dissipative silencer containing mean flow and a perforated pipe [J]. Journal of Acoustical Society of America. 2007, 122: 3471-3482.
[10]Munjal M L. Acoustics of ducts and mufflers [M]. Wiley-Interscience, New York, 1987.
[11]徐贝贝,季振林.穿孔管阻性消声器声学特性的有限元分析[J].振动与冲击,2010, 29(3): 58-62.
XU Bei-bei, JI Zhen-lin. Finite element analysis of acoustic attenuation performance of perforated tube dissipative silencers[J], Journal of Vibration and Shock, 2010, 29(3): 58-62.
[12]Ji Z L, Fang Z, On the acoustic impedance of perforates and its application to acoustic attenuation predictions for perforated tube silencers[C]. Inter-noise 2011, Osaka, Japan, September, 201.
[13]Morse P M, Ingard K U. Theoretical acoustics[M]. Princeton University Press, Princeton, (1986).
[14]方智,季振林,穿孔管消声器横截面模态及消声特性的有限元分析[J],振动与冲击,2012, 31(17): 190-194.
FANG Zhi, JI Zhen-lin. Finite element analysis for cross-sectional modes and acoustic attenuation characteristics of a perforated tube silencer[J]. Journal of vibration and shock, 2012, 31(17): 190-194.
[15]Lee I. Acoustic characteristics of perforated dissipative and hybrid silencers[D]. PH. D thesis. The Ohio State University, Columbus, American, 2005.
