一种水下声信号未知频率的时延差估计方法

郑恩明，陈新华，孙长瑜

(1.中国科学院 声学研究所,北京 100190；2.中国科学院大学 北京 100190)

在被动三元阵测距声呐应用中，随着减振降噪技术的不断提高，目标辐射噪声相比环境噪声在不断地降低，致使声呐设备对其接收信号所能提供的先验知识也在不断地减少。常规时延估计算法在被动声呐时延差估计中已不能满足对水下远程目标的定位需求。正如文献[1-6]所述，水下目标螺旋桨转动会切割水体产生低频信号，其中部分信号会直接以加性形式出现在目标辐射信号中，部分信号则被船体本身的振动调制到较高的频带。在目标辐射信号中线谱通常比连续谱要高出10～25dB，这为实现水下目标远程定位提供了一种可能。对此，本文将文献[7-9]的所提出的基于频率方差或基于方位方差的目标检测方法引用到本文中，以便实现被动声呐定位中所需的时延差估计。本文利用噪声对应频率单元互相关谱最大值随机，目标对应频率单元互相关谱最大值基本一致的特点，统计各频率单元的时延差估计结果可得最终时延差估计值，理论分析和仿真结果表明：该方法具有较好的有效性，对信噪比的宽容性远好于频域互相关法。该方法为弱线谱时延差估计提供了一个参考思路。

本文接下来将探讨高斯宽带噪声背景下，如何利用各频带对应时延差方差形成的时延差方差加权因子进行时延差估计。本文安排如下：第1节给出了阵元接收目标辐射信号模型；第2节介绍了未知信号时延差估计方法；第3节基于时延差稳定性时延差估计的性能分析；第4节为实验分析；第5节为本文结论。

1 信号模型

1.1 目标辐射信号模型

水下目标辐射信号简化形式可表示为

(1)

式中：Am为单频信号的幅度，fm为单频信号的频率，φm为单频信号的随机相位，t为目标辐射信号时刻，n(t)为宽带噪声信号；M为假定的独立分量数，φm和n(t)相互独立，φm服从[0～2π]均匀分布，单频信号与宽带连续谱信号谱级比为(SLR)|f=fm=10～25 dB。

1.2 阵元接收信号模型

阵元接收信号模型示于图1。

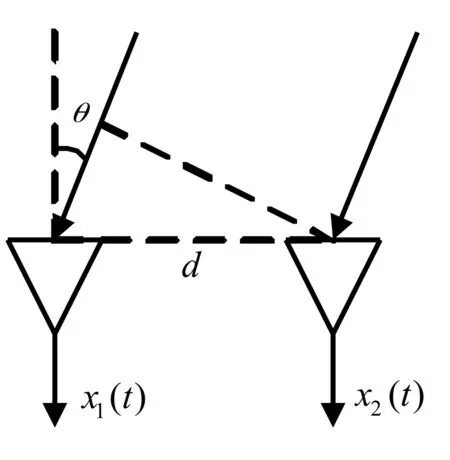
图1 阵元接收信号模型

目标辐射信号经水声信道传播后，阵元1、2接收信号形式可表示为(只考虑直达声的情况下)

(2)

2 未知信号时延差估计方法

2.1 频域互相关时延差估计

在传统宽带信号时延差估计中，常采用互相关法实现阵元间时延差估计。频域互相关时延差估计可按图2所示流程进行求解。

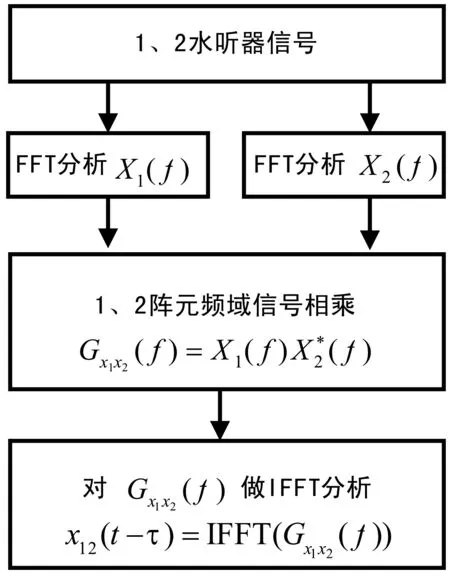
图2 频域互相关时延差估计流程图

根据图2可知：当目标辐射线谱信号未知时，常规方法在求两阵元接收信号时延差τ时，会将接收信号的所有频率单元等价地应用到时延差估计中[10-13]。由于其他频带基本是噪声，无线谱信号，此时的时延差估计结果误差比较大。对此，本文采用下述方法对常规方法进行改进，以便突出线谱信号在整个频带中的比重。

2.2 基于线谱时延差稳定性时延差估计

当目标辐射线谱信号每次均能稳定的实现时延差估计，统计时间内时延差变化缓慢时，可以采用下述方法实现对阵元1、2间时延差的有效估计。

设频率单元共K个，记为fi，i=1,…,K,时延差共L个，记为τj，j=1,…,L；其中L=d·fs/c[10]，d为阵元间距，fs为采样率，c为有效声。

首先对各阵元接收信号做快速傅里叶变换分析得到K个频率单元，记为fi,i=1,…,K，然后对每个频率单元进行互相关处理得到各频率单元的相关谱R(fi,τj)为K×L为矩阵。对每个频率单元求取最大值，则最大值的位置即为该频率单元的时延差估计初值，记为τ(fi)，i=1,…,K。由理论分析可知，目标辐射线谱信号对应频率单元所得τ(fi)应当为阵元间时延差真值，是稳定的；而背景噪声对应频率单元所得τ(fi)是随机的。

对上述信号处理过程重复N次，即连续处理N帧数据信号后再进行下一步处理，可得到每个频率单元对应的N个时延差，记为τn(fi)，i=1,…,K，n=1,…,N。分别计算每个频率单元的时延差方差，记为δτ(fi)，i=1,…,K。噪声对应频率单元的时延差是随机的，方差较大，而对于目标线谱对应的频率单元的时延差是基本不变的，方差很小。

然后对每一个时延差进行统计计算，作为最终相关谱输出，进而可得到最终时延差估计值。计算过程如下，首先将最后相关谱置0，即Rout(τj)=0,j=1,2,…L，接下来将所有频率单元的所有时延差均参与计算，当某一个频率单元的某一帧时延差为τn(fi)时，则在τn(fi)的对应值上累加该频率单元对应时延差方差的倒数，即

Rout(τn(fi))nn=Rout(τn(fi))nn-1/δτ(fi),

i=1,…K;n=1,…,N;nn=1,…。

(3)

以此计算，直到每一个频率单元每一帧的时延差均参与计算，最后得到每一个时延差方差倒数的累计值，作为最终相关谱输出值，进而可得到最终时延差估计值。本方法流程图如图3所示。

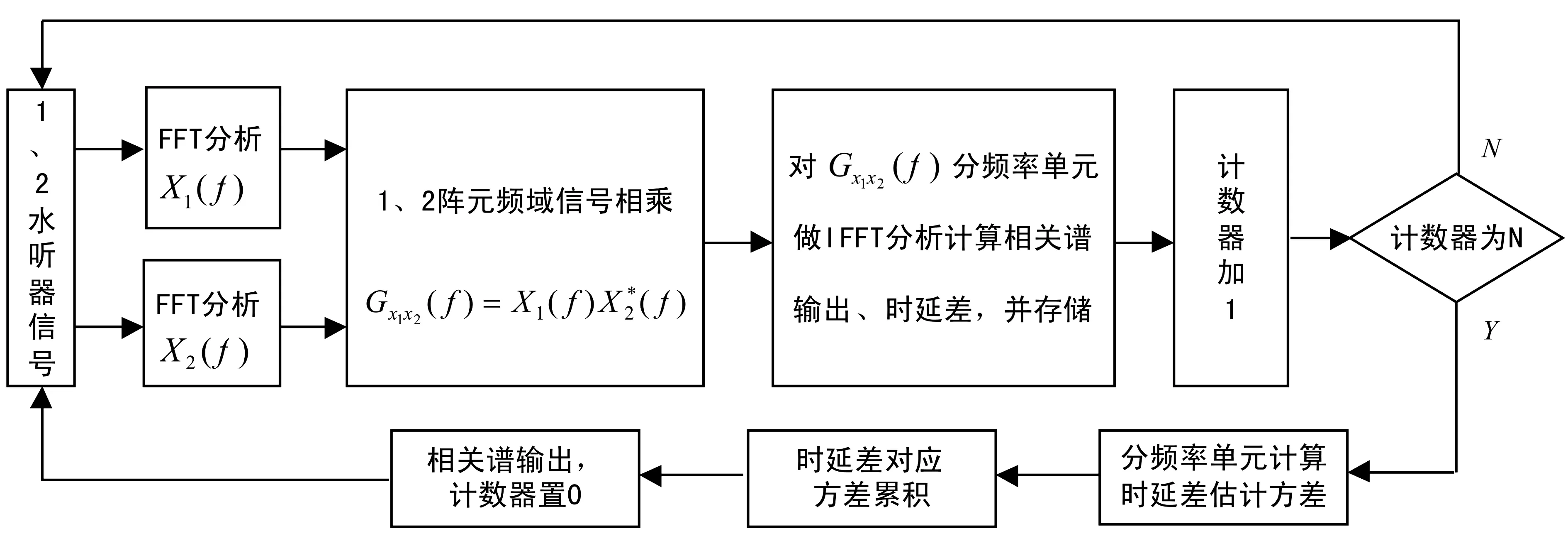
图3 基于时延差稳定性的时延差估计流程图

实现上述算法可分为以下5步：

(1)对水听器阵元1、2接收信号做快速傅里叶变换分析，然后对每一个频率单元进行频域互相关，从而得到每一个频率单元的相关谱输出值，记为R(fi,τj)；

为了得到阵元1、2接收信号每一个频率单元频域互相关谱，本文采用下式求解:

(4)

式中：FFT为快速傅里叶变换函数，X1(t)为阵元1接收信号，X2(t)为阵元2接收信号，fs为采样率,O*为复共轭。从式(4)可知，GX1X2(f)为X1(t)与X2(t)的互功率密度函数，其包含所有频率信号，如果直接对GX1X2(f)做逆快速傅里叶变换(IFFT)，其结果为常规频域相关法。对此，本文采用引导信号来求取每一个频率单元频域互相关谱。

(5)

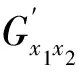
(2)对每一个频率单元的相关谱输出求取最大值，其所在位置即为每一个频率单元的时延差估计结果，记为τ(fi)；

(3)更新接收信号，重复进行第(1)步、第(2)步，直到重复次数达到预先设定值N，则每一个频率单元均得到N个时延差估计结果，记为τn(fi)；

(4)分别对每一个频率单元的时延差估计结果进行方差计算，对应结果记为δτ(fi)；

(5)对所有时延差估计结果对应的方差进行累计计算，作为最终相关谱输出值，例如当某一频率单元某一时刻的时延差估计结果为τn(fi)时，则在其相关谱输出值(Routτn(fi))上累加该频率单元对应的时延差方差倒数，如式(3)所示。

3 基于线谱时延差稳定性时延差估计性能分析

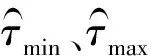
(6)

首先对噪声频率单元进行统计，即对个K-1频率单元进行统计

j=1,2,…,L

(7)

即对于噪声的相关谱输出值，每个预成时延差输出值是相等的，然后进一步将线谱估计时延差方差结果累加到式(7)表示的结果，可得：

Rout(τj)=

(8)

进一步简化为

(9)

因此当线谱时延差方差很小时，即每帧时延差估计结果均接近于阵元1、2接收信号的时延差真值，即δs值较小，比较式(7)和式(9)可以看出阵元1、2接收信号真实时延差附近的相关谱出值将远大于其它时延差相关谱输出值。

4 实验分析

假设目标相对于阵元1、2的方位为60°，辐射信号包括高斯带限白噪声和线谱成份，白噪声带宽为60～300 Hz，线谱频率为100 Hz，线谱与白噪声平均谱级比为18 dB。目标辐射信号对应的频谱如图4(a)所示。干扰为带限白噪声，目标辐射噪声谱级与干扰噪声谱级比为-16 dB，则阵元1、2接收信号的线谱与干扰噪声平均谱级比为2 dB。

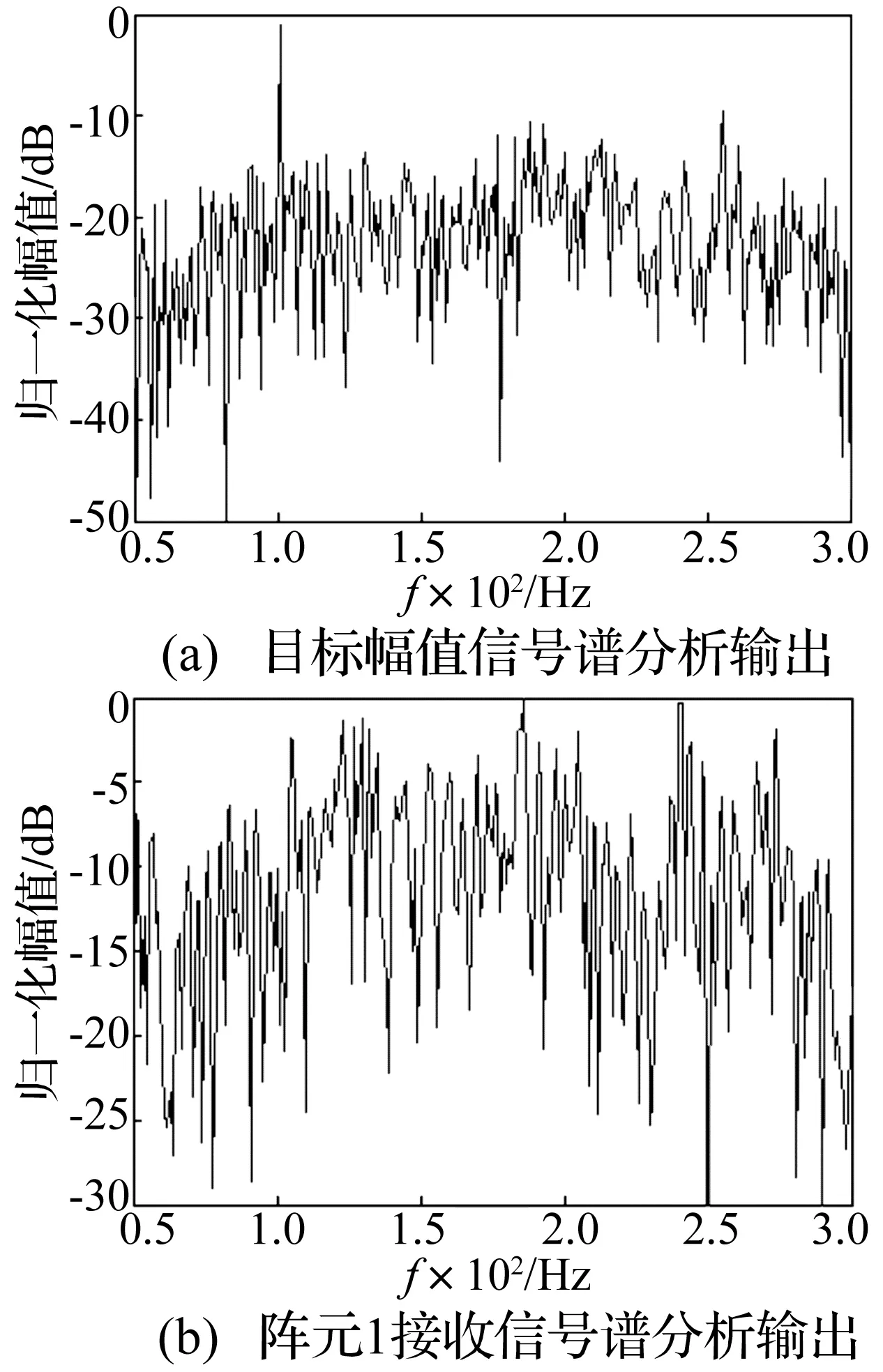
图4 信号谱分析输出图

从图4(a)可以明显得到目标在频率100 Hz处有强线谱存在，但从图4(b)阵元1接收信号中却不能得到目标辐射线谱信号位置。如果采用常规相关法求取时延差，干扰噪声与线谱信号在整个相关谱中的比重一样，低信噪比下不能实现时延差估计。

现假定阵元1、2间距为15 m，有效声速为c=1 500 m/s，对先前设定信号按采样率为fs=2 500 Hz，由此可得阵元1、2接收信号的时延差点数为τ=d·fs·cos(π/3)/c≈13；现一次采集长度为T=10 s阵元1、2拾取数据，对采集数据分10段，每段分240个频带进行按两种方法进行仿真分析：第1种方法是基于频域互相关法，即对整个频带采用互相关来求取阵元间接收信号时延差；第2种方法是基于时延差稳定性法即本文所述方法；对每一个频率单元进行处理，估计每一个频率单元对应的时延差，最后进行时延差统计得到最终时延差估计值。仿真结果如图5、图6所示，根据图5可知，基于频域互相关法不能实现对阵元1、2接收信号的时延差估计；而根据图6可知，本文所述方法可以有效实现对阵元1、2接收信号时延差估计(由于MATLAB仿真中是从1开始，所以图中14即为13)。

图5 频域互相关时延差估计结果

图6 基于时延差稳定性时延差估计结果

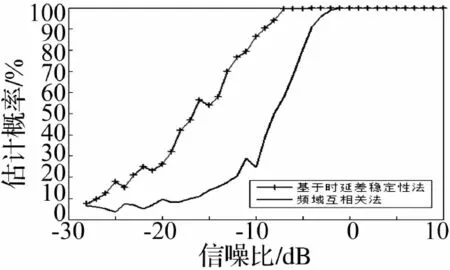
图7 不同信噪比下，两种方法的时延差估计概率

为了验证不同信噪比下，本方法与频域互相关的时延差估计概率。本文将采用如下的仿真条件进行MATLAB实验分析，目标相对于阵元1、2的方位为60°，辐射信号只有线谱成份，干扰噪声带宽为60～300 Hz，线谱频率为100 Hz。图7给出了线谱与干扰噪声信噪比为SNR=-28～10 dB时，采用本方法与频域互相关进行100次独统计所得时延差估计概率。

从图7中可以得到，本文所述方法在SNR=-16 dB时的时延差估计概率大于50%，而频域互相关法在SNR=-7 dB时的时延差估计概率已小于50%；且在SNR=-16～-5 dB时，本方法相比频域互相关法的时延估计概率高出40%。图7的仿真结果表明本方法时延差估计对信噪比的宽容性远好于频域互相关法。

5 结 论

本文介绍了一种针对目标辐射信号中线谱不确知的时延差估计方法。首先对接收信号做快速傅里叶变换，然后求取每一个频率单元所对应的时延差初值，利用噪声频率单元时延差估计结果随机，而目标线谱时延差估计结果一致的特点，最后对每一个时延差估计结果进行统计得到阵元1、2接收信号的最终时延差估计。理论分析和MATLAB数值仿真验证了本方法在目标辐射信号具有稳定线谱的情况下，时延差估计对信噪比的宽容性远好比频域互相关法。但由于本文所述方法需要得到每一个频率单元的相关函数，为了避免相关函数多值性的出现，本文在求取每一个频率单元的时延差时进行了限定即为-d/c≤τ≤d/c；在使用本文方法时，可结合频域内插法得到较高的时延差估计精度。

[1]McDonough R N，Whalen A D.Detection of signals in noise.2nd Ed[C].Academic Press，USA，1995.

[2]Urick R J.Principles of underwater sound[M].New York: McGraw-Hill Book Company,1983.

[3]Ross D.Mechanics of underwater noise[M].New York: Pergmin Press,1976.

[4]吴国清,李靖.舰船噪声识别-线谱稳定性和唯一性[J].声学学报,1999,24(1):6-11.

WU Guo-qing，LI Jing.Ship radiated-noise recognition-stability and uniqueness of line spectrum[J].Acta Acustica，1999,24(1):6-11.

[5]李启虎,李敏,杨秀庭.水下目标辐射噪声中单频信号分量的检测:理论分析[J].声学学报,2008,33(3):193-196．

LI Qi-hu，LI Min，YANG Xiu-ting．The detection of single frequency component of underwater radiated noise of target :theoretical analysis[J].Acta Acoustica，2008,33(3):193-196.

[6]李启虎,李敏,杨秀庭.水下目标辐射噪声中单频信号分量的检测:数值仿真[J].声学学报，2008，33(4): 289-293.

LI Qi-hu，LI Min，YANG Xiu-ting.The detection of single frequency component of underwater radiated noise of target: digital simulation [J].Acta Acoustica，2008，33(4): 289-293.

[7]陈阳,王自娟,朱代柱,等.一种基于频率方差加权的线谱目标检测方法[J].声学学报,2010,35(1): 76-80.

CHEN Yang，WANG Zi-juan，ZHU Dai-zhu,et al.A detecting method for line-spectrum target based on variance of frequency weight[J].Acta Acoustica，2010，35(1): 76-80.

[8]陈阳,赵安邦,王自娟，等.瞬时频率方差加权导向最小方差波束形成检测器[J].哈尔滨工程大学学报，2011，32(6): 730-735.

CHEN Yang，ZHAO An-bang，WANG Zi-juan,et al.Variance of instantaneous frequency-weighted steered minimum variance beamforming detector[J].Journal of Harbin Engineering University，2011,32(6):730-735.

[9]陈新华,鲍习中,李启虎，等.水下声信号未知频率的目标检测方法研究[J].兵工学报,2012,33(4): 471-475.

CHEN Xin-hua,BAO Xi-zhong,LI Qi-hu.et al.Research on detection of underwater acoustic signal with unknown frequency[J].Acta Armamentarii，2012，33(4): 471-475.

[10]张卫平,张合,王伟策,等.基于两次谱分析的时延估计方法研究[J].应用声学,2008，27(3):222-226.

ZHANG Wei-ping，ZHANG He，WANG Wei-ce，et al.Time delay estimation by two times spectral analysis [J].Applied Acoustics，2008，27(3):222-226.

[11]蒋伊琳，司锡才.基于互相关和MUSIC算法的时延估计[J].弹箭与制导学报，2009,29(5): 208-211.

JIANG Yi-lin，SI Xi-cai.Time delay estimation based on cross-correlation and multiple signal classification [J].Journal of Projectiles，Rockets，Missiles and Guidance，2009,29(5): 208-211.

[12]黄清.相关域双谱时延估计方法[J].声学学报，2003，28(1): 57-60.

HUANG Qing.BisPectrum time delay estimating based on correlation[J].Acta，Acustica，2003，28(1): 57-60.

[13]童峰,许肖梅,方世良.一种单频水声信号多径时延估计 算法[J].声学学报，2008，33(1): 61-67.

TONG Feng，XU Xiao-mei，FANG Shi-liang.MultiPath time-delay estimation of underwater acoustic sinusoidal signals[J].Acta，Acustica，2008，33(1): 61-67.