基于动刚度理论的柔性组合式起重机减振方法研究

张大海， 吴邵庆， 韩晓林

(东南大学 工程力学系 江苏省工程力学分析重点实验室，南京 210096)

1 问题描述

桥式起重机为横架于车间、厂房及仓库上空的起重设备。柔性组合式起重机作为桥式起重机的一种，具有结构紧凑、拆装方便、操作简单等优点，广泛应用于工业生产中[1-2]。由于目前吊挂系统设计主要采用基于静强度准则并考虑动载系数方法[3]，无法考虑吊挂过程中所受冲击载荷产生的振动。易引起吊装系统吊装重物时产生冲击载荷作用下发生幅值较大振动。

本文研究吊装系统为某品牌型号柔性组合式起重机，包括立柱与钢屋架、下方钢支架、吊挂在钢支架下的柔性组合式起重机及工件。吊装系统简图见图1，钢屋架各跨间距离8 m，立柱高12.8 m，钢屋架高2.7 m，钢支架高2.3 m，钢屋架与钢支架间距0.6 m。起重机见图2，由①纵梁(长11 m)，②横梁(长5.5 m)，③环链电动葫芦(质量20 kg)，④悬索组成。纵梁由6个吊挂装置吊挂在钢支架梁上，横梁与纵梁间及电动葫芦与横梁间分别用环形吊具吊挂，横梁可沿纵梁整体移动，电动葫芦可沿横梁自由移动，工件(质量125 kg)通过悬索吊挂在电动葫芦下方，通过操控电动葫芦使其上下移动。

图2 单梁悬挂起重机

图3 连接部位细节图

各连接细节见图3，图3(a)、(b)、(c)分别为纵梁与支架梁间连接、横梁与纵梁间连接及横梁与电动葫芦间连接。起重机工作过程中横梁与电动葫芦均可移动。工件运动状态变化会使系统受到惯性冲击载荷，引起系统振动。由力学角度该系统可视为时变系统[4]，其动力学特性随横梁及电动葫芦位置变化而变化。

由《起重机设计规范》(GB3811-2005)知，对一般起重机不规定校核动态刚度，但有要求(如：认为对起重机司机健康有影响)时则进行校核，并可用满载自振频率表征。由于本文研究吊装系统中，钢支架仅考虑静强度准则设计，导致在重物吊装时停顿引起的惯性冲击载荷作用下振动幅值过大，且衰减缓慢，严重影响操作及工件吊装效率，故须校核动态刚度。

本文由动态设计角度研究该柔性组合式起重机吊挂工件过程中出现的振动问题：① 对该起重机在工件吊挂过程中的振动现场测试，据测试数据分析结果，由提高结构动刚度角度提出能减小工件吊挂过程中振动幅值方案；② 对吊挂系统进行有限元建模及多种减振方案仿真、减振效果分析，为解决同类结构在安装、使用中出现的振动问题提供参考。

2 桥式起重机动态刚度

桥式起重机刚性要求包括静刚度与动刚度两方面，其中动刚度指起重机在工作时系统结构抵抗动载荷引起变形的能力，为衡量桥式起重机动力学特性的重要指标[5-6]。动刚度通常以系统动力响应表征，定义为产生单位振幅所需动态力。图4为受简谐激振力F=A0sin(ωt)的单自由度系统。其中A0，ω分别为简谐力振动幅值、圆频率；M，C，K分别为该系统质量、阻尼、刚度。其动刚度KD可表示为：

KD=K[(1-λ2)+2iξλ]

(1)

式中：λ为激励频率与系统固有频率之比；ξ为系统阻尼比。

动刚度幅值Kd为：

(2)

式(2)表明，单自由度系统动刚度为随激振频率变化的函数。

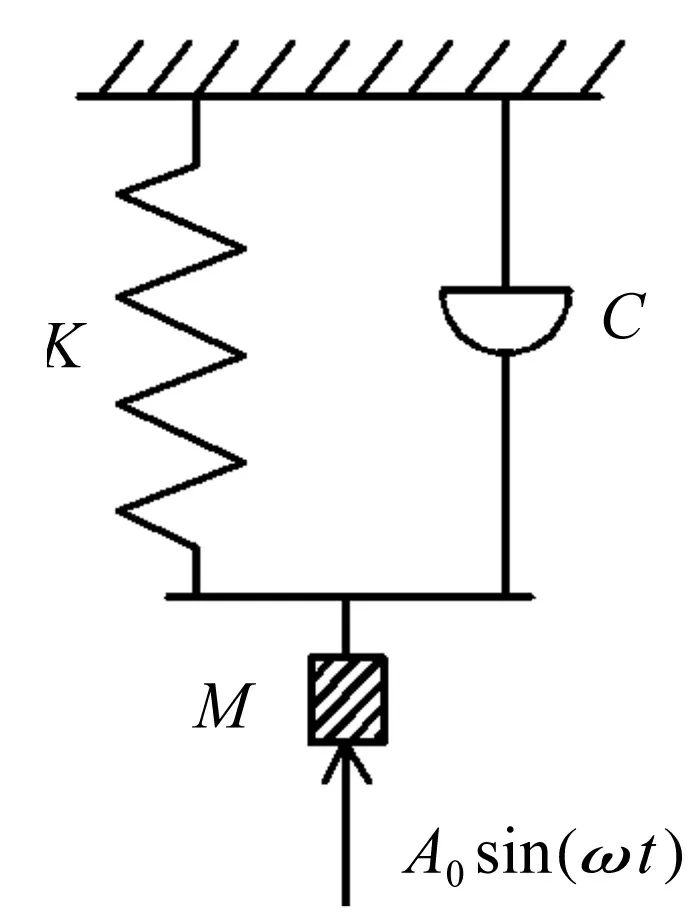
图4 受简谐力作用的单自由度系统

起重机起吊、卸载、变速时使被吊挂工件产生加速度a，引起工件附加大小为Ma的惯性冲击动载荷，其中M为工件质量。吊挂系统受到惯性冲击载荷作用引起系统随工件整体振动。影响工件振动幅值大小因素有：外界载荷大小、结构自身竖向动刚度及结构自身衰减特性等。本文主要研究通过改进结构自身设计减小工件吊挂的振动幅值。对图4中有阻尼单自由度系统，振幅由X0衰减为Xn所需时间为[7]：

(3)

由式(3)知，设阻尼比ξ为常数，则衰减时间T与自振频率fn成反比。通常起重机由起、制动冲击荷载引起的衰减振动频率为一阶固有频率[7]，振型为吊重与主梁上下同步振动。因此，起重机设计规范推荐用垂直方向振动一阶固有频率表征起重机动刚度时，一阶固有频率f0应不低于2 Hz。此外，由规范，本文所研究类型起重机工作级别为A3级，其挠度为：

(4)

式中：u为垂直挠度；L为起重机跨度。本文起重机跨度L为5.5 m，故垂直挠度应该满足u≤7.86 mm。

3 振动测试

3.1 测试工况及传感器布置方案

测试在最不利情况即振动幅值最大时进行。起重机横梁位于离纵梁端点1.78 m处，电动葫芦吊挂于横梁中点。加速度传感器布置见图5，各测点位置说明见表1。通过间歇性开动、停止电动葫芦引起工件振动激振整个吊挂系统。

3.2 测试结果分析

测试得振动垂直挠度10.13 mm。各测点加速度信号见图6。各测点加速度峰值及基频数据见表2，其中基频数据由各加速度信号频谱分析获得。

图5 传感器布置示意图

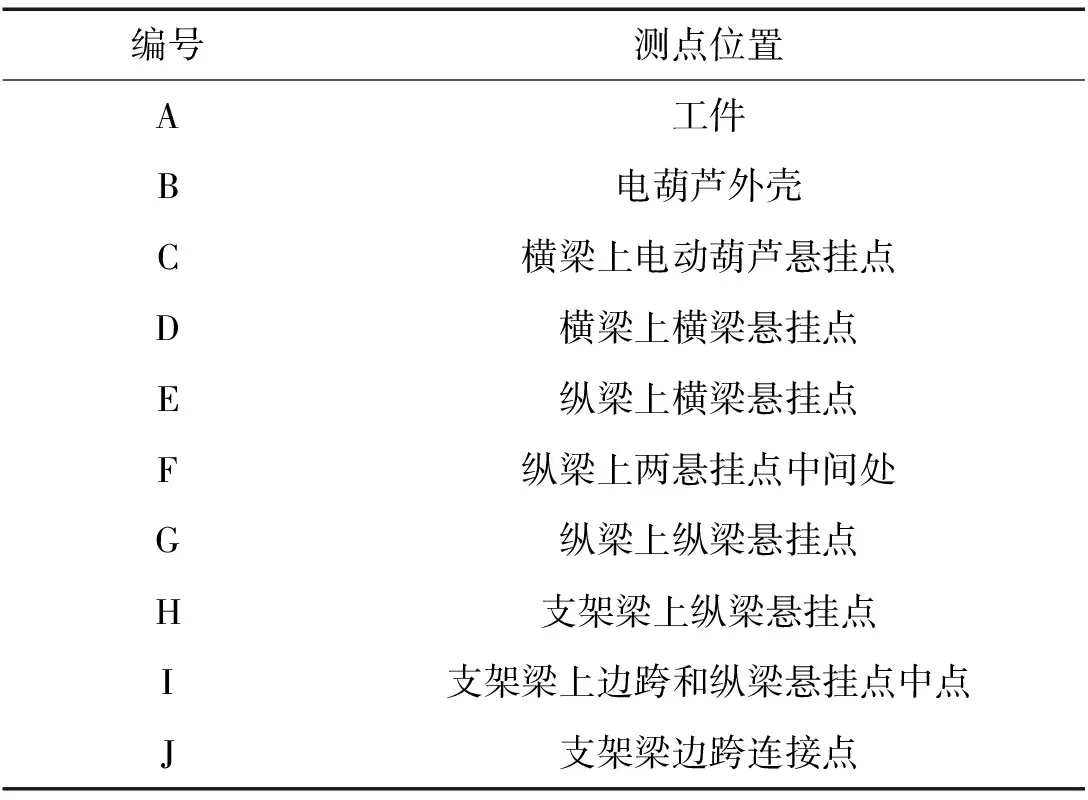
表1 各测点位置说明

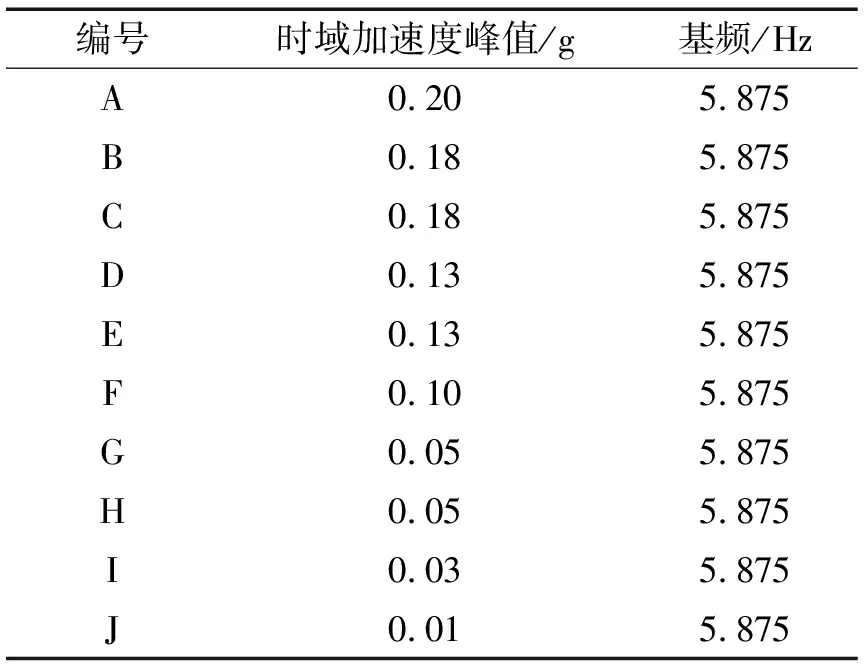
表2 各点测试结果

测试结果表明：① 分析各加速度信号频谱知，系统发生整体振动，且振动基频为5.875 Hz，虽满足规范对动刚度基频不小于2 Hz要求，但各吊点阻尼比较小，约0.3%，导致振动衰减较缓慢；② 垂直挠度大于规范值，表明整个吊装系统动刚度不足；③ A点振幅大于B点，说明电动葫芦内部结构及悬索会导致振动幅值变大；④ B、C点，D、E点，G、H点振动两两基本一致，表明各连接能较好传递竖向振动，刚性较强；⑤ D、C点振动趋势基本一致，幅值较小，结合E点振动信号可知横梁振动包含跟随纵梁的竖向整体振动及自身弯曲振动；⑥ E、F、G点振动逐渐降低，说明纵梁发生明显竖向弯曲振动，竖向刚度不足。同理，H、I、J点振动逐渐降低，表明纵梁上方钢梁支架有明显弯曲振动，竖向刚度不足。

图6 各测点加速度响应

3.3 系统加固方案

系统动刚度不足可能为：起重机纵梁、横梁本身刚度不足；纵梁吊点太少导致纵梁跨度过大；厂房结构、钢支架刚度不足等。由提高结构动刚度角度，提出系统加固方案为：① 在起重机横梁与纵梁上方加焊T型梁加固；② 纵梁上方加并行梁并增加吊点，提高纵梁刚度；③ 在钢支架与刚度较大的钢屋架间增加竖向吊杆加固。

4 有限元仿真及验证

4.1 吊装系统有限元建模

4.1.1 起重机建模

建立(图2)柔性组合式起重机测试工况有限元模型。悬索用三维杆单元模拟；横梁、纵梁及各部件连接用三维线性梁单元模拟；环链电动葫芦及工件用集中质量单元模拟，见图7。

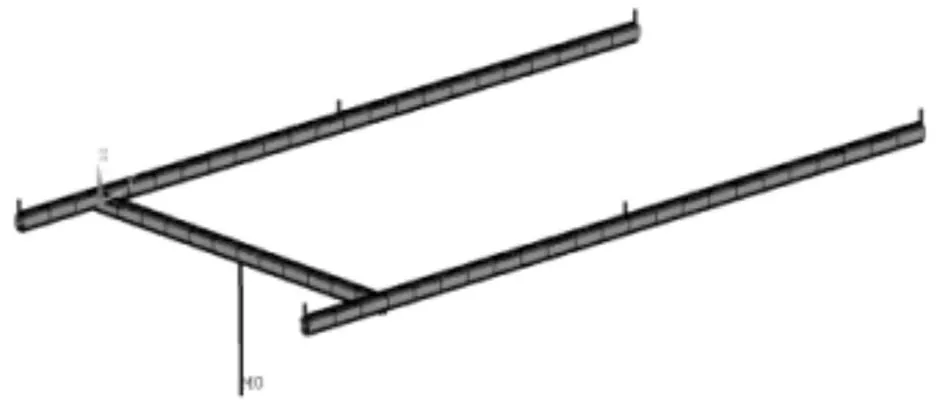
图7 起重机有限元模型

4.1.2 总体结构建模

厂房整体为钢结构，各部件均用相同截面三维梁单元模拟。见图8。

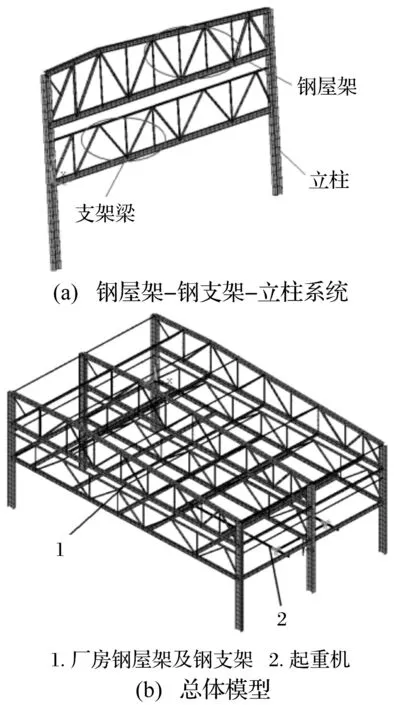
图8 总体结构有限元模型

4.2 基于有限元模型的动力学分析

4.2.1 模态分析

4.2.1.1 起重机模态分析

图9 起重机横梁一阶振型图

对起重机进行模态分析，前五阶模态均为纵梁水平方向模态，模态频率见表3。第六阶模态含横梁、纵梁整体竖向振动模态，见图9(a)，振动频率为5.786 Hz，与振动测试分析结果较接近。若将工件吊挂点移至横梁1/4跨处，起重机系统模态频率提升至7.003 Hz，模态振型见图9(b)，说明该系统动力学特性随工件吊挂位置不同而改变，工件吊挂位置对起重机系统动刚度有一定影响，体现出该系统“时变”特性。

表3 起重机前六阶模态频率

对3.3节中前两种加固方案进行有限元模拟及模态分析。加固前后模态振型出现顺序发生改变，模态频率见表4。由表4看出，综合前两种方法后，横梁与纵梁振动第一阶竖向固有频率由原5.786 Hz提高至加固后10.642 Hz，表明系统静刚度的提高，据式(1)知系统动刚度KD与静刚度K成正比，因此系统固有频率的提高亦表明系统动刚度提高。

（3）引进大数据处理的相关技术人员。在大数据时代下建设新型电网规划体系需要多方面技术人员的共同合作和努力，大数据不仅仅与计算机科学技术相关，它还涉及到社会经济、电子信息、社会调查等多个学科领域，所以除了电力人员以外，引入大数据相关的专业性人才是非常有必要的，这对新型电网规划体系的建设有着十分重要的意义。

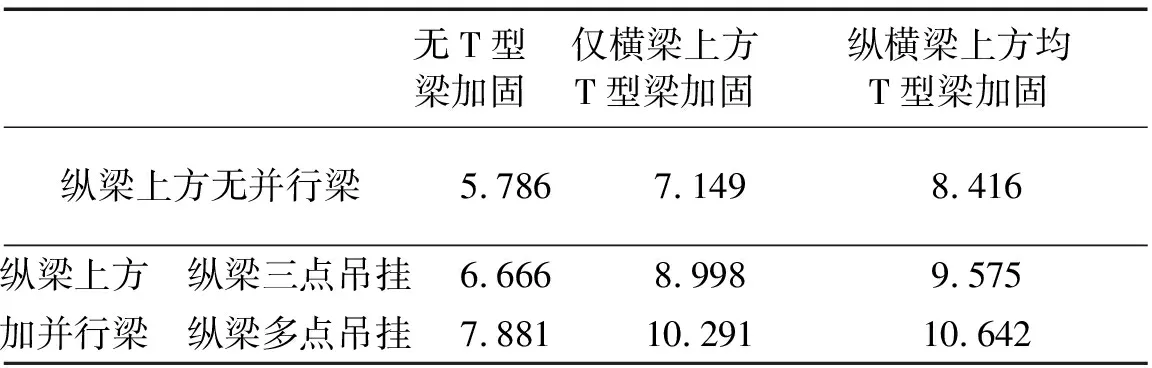
表4 各加固工况横梁一阶竖向模态频率(Hz)

4.2.1.2 钢屋架-钢支架-立柱系统模态分析

对图8(a)系统进行模态分析知，前两阶竖向模态频率为12.854 Hz、13.859 Hz。钢屋架及钢支架相向运动与同向运动振型见图10(a)、(b)。用加固方案三后，系统一阶竖向振型变为与加固前二阶类似，频率为13.911 Hz，而钢屋架与钢支架相向运动模态消失。证明该加固方法能提高结构动刚度。

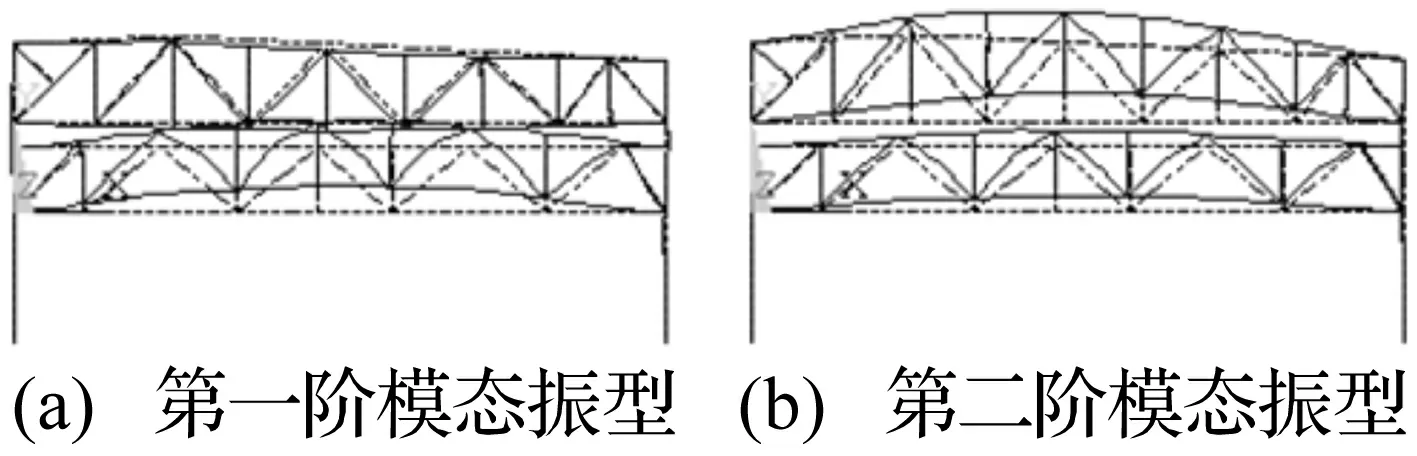
图10 钢屋架-钢支架-立柱系统前两阶竖向振型

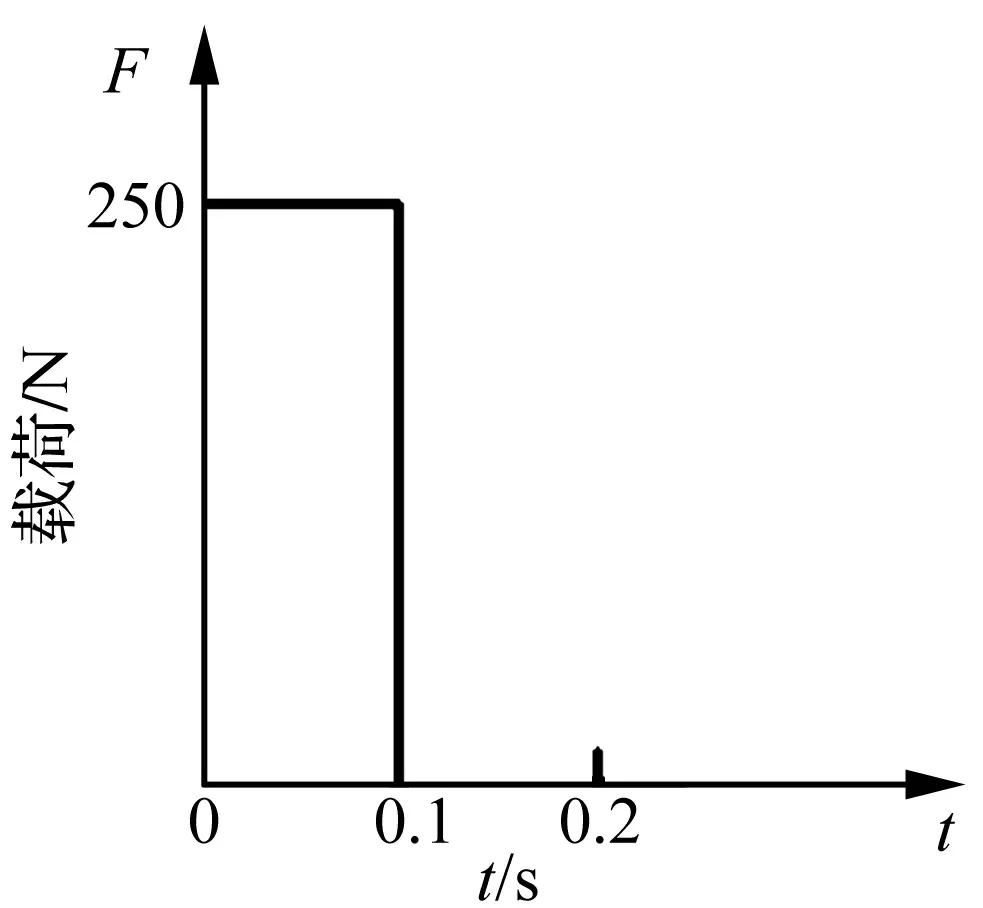
图11 工件处施加突变荷载

4.2.2 动响应分析

在工件处施加突变动载荷，模拟吊挂时工件运动状态突变引起作用于工件的惯性冲击动载荷。动载荷F=Ma=250 N。M=125 kg为工件质量，a=0.2 g为工件在外载荷冲击下加速度，持时0.1 s，见图11。在此冲击载荷下对系统进行动响应分析[8]。

图12为用三种加固方案前后工件的振动位移时程对比(虚线为减振前，实线为减振后)。表5为加固前后工件处最大振动幅值变化。由分析结果知，分别采用3.3节中三种系统加固方案，工件处最大振动幅值可减小50%、25%、11%。综合三种减振方法后，整个吊装系统含纵梁、横梁振动的一阶竖向模态频率由5.786 Hz提高到11.594 Hz，竖向动刚度得到大幅度提升，工件处振动幅值减小67%，垂直挠度完全达规范要求。振动衰减速率显著加快，其原因为：① 由式(3)知衰减时间与自振频率成反比， 加固后系统自振频率提升，衰减时间缩短；② 加固后附加结构提高了系统阻尼。

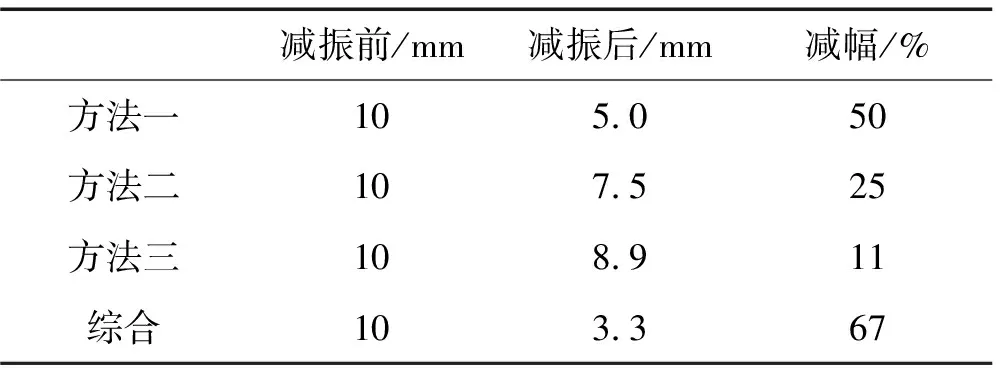
表5 减振处理前后最大振幅

图12 减振处理前后工件处位移时程

5 结 论

本文以某单梁柔性组合式起重机为例，由系统动刚度概念出发研究起重机在吊挂工件过程中出现的工件振动幅值过大、振动衰减过慢问题。通过分析现场测试数据，提出三种系统加固方案，并通过有限元仿真获得各方案减振效果。通过研究该类柔性组合式吊装系统的动力学特性及减振方案，结论如下：

(1) 本文认为起重机吊挂时工件处振动幅度过大、衰减缓慢主要原因在于系统动刚度不足、阻尼较小。用所提加固方案能较有效解决工件吊挂过程中振动问题；

(3) 起重机上方钢支架竖向动刚度不足亦会导致系统振动过大、衰减过慢。可通过加固钢支架并将支架与刚度较大的钢屋架用竖向吊杆相连接方法增加竖向动刚度。通过加固，吊装系统一阶竖向振动频率由5.786 Hz提高到11.594 Hz，工件位置最大振幅减小67%，垂直挠度达到规范要求，且衰减速度明显加快，系统减振效果较好。

参 考 文 献

[1]李 泉,倪大全.关于柔性组合式悬挂起重机检验中一些问题的探讨[C]. 中国力学学会学术大会论文集,2009.

[2]Fang Y, Dixon W E,Dawson D M,et al.Nonlinear coupling control laws for an underactuated overhead crane system[J]. Transactions on Mechatronics,2003,8(3):418-423.

[3]曾 春. 基于ANSYS的桥式起重机桥架结构有限元动态分析研究[D].武汉:武汉理工大学,2006.

[4]Spruogis B,Jakstas A,Turla V, et al. Dynamic reaction forces of an overhead crane on lifting[J]. Transport,2011, 26(3):279-283.

[5]王金诺，于兰瑞. 起重运输机金属结构[M]. 北京: 中国铁道出版社,2002.

[6]Oguamanam D C D,Hansen J S,Heppler G R. Dynamics of a three-dimensional overhead crane system[J].Journal of Sound and Vibration, 2001,242(3):411-426.

[7]王创民，高俊云，王首成. 桥式起重机动刚度计算的建模与分析[J]. 起重运输机械,2008,12:87-91.

WANG Chuang-min,GAO Jun-yun,WANG Shou-cheng. Modeling and analysis of the bridge crane dynamic stiffness [J]. Hoisting and Conveying Machinery, 2008, 12: 87-91.

[8]嘉红霞，李万莉，William Singhose. 考虑臂架弹性的动臂起重机动力学建模及振动分析[J]. 振动与冲击,2010,29(12): 136-140.

JIA Hong-xia, LI Wan-li, Singhose W. Dynamic modeling and vibration analysis of cherry pickers with flexible arms [J]. Journal of Vibration and Shock, 2010,29(12):136-140.