基于谐波平衡法的双稳态压电发电系统非线性振动特性研究

贾尚帅， 孙 舒， 李明高

(1.唐山轨道客车有限责任公司 产品技术研究中心，河北 唐山 063035；2.河北联合大学 理学院，河北 唐山 063009)

压电式结构为常用发电结构形式。目前研究的压电发电系统多为线性，具有单一固有频率。而实际环境振动常为非周期、随机、宽频激励。双稳态压电系统在周期或随机激励下，可在低宽频下产生大幅运动，为最可能实现利用振动发电的结构之一[1]。

Erturk等[2-3]将Moon与Holmes双稳态模型[4]用于压电发电，通过实验及数值计算分析双稳态压电悬臂梁响应与输出特性。Stanton等[5]通过对双稳态压电发电悬臂梁建模、数值计算及实验研究，获得叉形分岔的对称破缺、多吸引子共存、混沌、大幅运动等现象。Andò等[6]给出工作在双稳态下的MEMS设备分析模型。Arrieta等[7-9]对双稳态压电板进行数值模拟及实验研究发现具有宽频带的亚谐共振大振幅周期运动及混沌运动，认为双稳态板适用作压电发电。文献[10]在建立非线性磁力模型基础上，建立双稳态压电悬臂梁集中参数模型，并进行数值分析、实验研究，获得双稳态系统在低宽频下能产生大幅运动及激励参数与永久磁铁间距对系统运动影响规律。

以上研究多集中于数值计算与实验，而数值方法只能获得系统的动力学行为轨迹，并不能对系统运动行为本质做出刻画。本文在文献[10]基础上，利用谐波平衡法获得系统频响方程，研究不同参数下频响特性及输出特性，并通过实验研究进行验证。

1 双稳态压电发电系统模型

双稳态压电发电系统通过加入磁力实现双稳态，将一块永久磁铁固定于悬臂梁自由端，磁铁处于水平位置时其中心至梁根部距离为l，将另一块磁铁固定在距自由端d处，见图1。由图1看出，当d足够大时，两磁铁间无作用力，系统为线性；当d缩小到一定程度时， 梁具有3个平衡点，其中2个稳定平衡点与1个不稳定平衡点表现出双稳态现象。

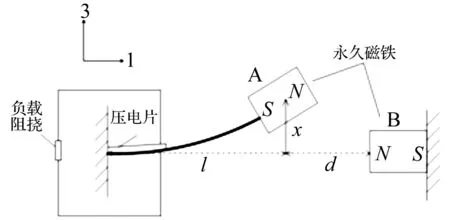
图1 双稳态压电发电系统模型

双稳态压电发电系统无量纲动力学方程[10]为：

(1)

其中:

(2)

式中：m为梁与磁铁等效质量；c为机械阻尼系数；k为悬臂梁弹性常数；μ0=4π×10-7H/m为真空磁导率；MA，MB为磁铁A，B磁化强度；F0为激励幅值；RL为负载阻抗；Cp为压电陶瓷等效电容；κv，κc为机械方程及电方程中机电耦合系数。

2 谐波平衡法求解

设式(1)的解为：

(3)

则：

(4)

将式(3)、(4)代入式(1)，常数项sin(Ωt)，cos(Ωt)系数为零，得：

(5)

(6)

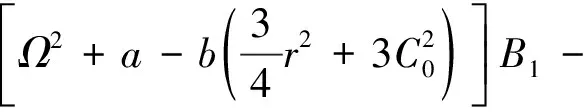
2ζΩA1+γB2+f=0

(7)

ΩB2-μA2+ϑΩB1=0

(8)

ΩA2+μB2+ϑΩA1=0

(8)

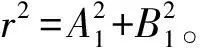
由式(8)、(9)得：

(10)

(11)

将式(10)、(11)代入式(6)、(7)化简得：

ΓAA1=ΓBB1

(12)

-f=ΓBA1+ΓAB1

(13)

其中：

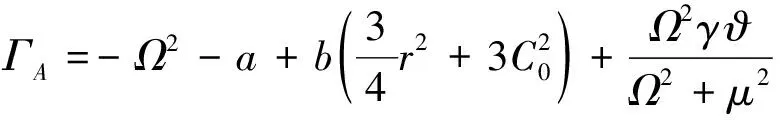
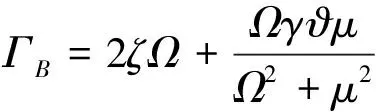
考虑式(12)、(13)得：

(14)

电压幅值为：

(15)

双稳态压电发电系统功率为：

(16)

3 系统非线性特性分析

3.1 幅频响应

取参数值ζ=0.05，a=0.5，b=25，γ=0.05，μ=0.7，ϑ=0.5，f=0.006。振幅r随激励频率变化时频率响应曲线见图2，其中虚线为不稳定部分。激励频率由小变大时，在Ω=0.85向上跳跃；激励频率由大变小时，在Ω=0.78向下跳跃；即在0.78～0.85区间系统出现多解现象，为不稳定区域。当系统的解被吸引到高能量解时，系统输出功率最大。分别分析磁化强度与负载阻抗对系统解影响。

由式(2)知，磁化强度MA，MB越大，非线性系数b值越大；负载阻抗RL越大，阻抗参数μ值越小。不同b，μ下幅频曲线研究磁化强度与负载阻抗对响应影响。b，μ取不同值时幅频响应曲线见图3、图4。由二图看出，随磁化强度MA，MB的增加，非线性系数b值增大，系统由低能量解跳到高能量解越不稳定，而共振幅值先增加后减小；调节阻抗参数μ可使不稳定区域最小。

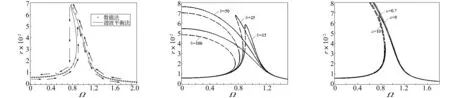
图2 幅频响应曲线

3.2 力幅响应

取参数值ζ=0.05，a=0.5，b=25，γ=0.05，μ=0.7，ϑ=0.5，Ω=0.77。力幅响应曲线见图5，其中虚线为不稳定部分。激励幅值由小变大，在f=0.012向上跳跃；激励幅值由大变小，在f=0.006 4向下跳跃；即在0.006 4～0.012区间系统出现多解现象，为不稳定区域。整体随激励幅值的增加，系统幅值逐渐增加，但增加幅度逐渐变小。b，μ不同值对应力幅响应曲线见图6、图7，随非线性系数b的增加，出现高能量解对应的激励幅值变小，但响应幅值亦变小；调节阻抗参数μ可使不稳定区域最小。

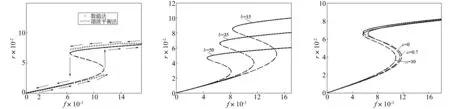
图5 力幅响应曲线

3.3 输出功率分析

由图8、图9看出，外加激励频率对功率影响与外加激励对振幅r影响相似。随非线性系数b的增大，不稳定区域变大，功率先增加后减小；对不同阻抗参数值μ，功率幅值先增加后减小，调节磁化强度及负载阻抗，对应非线性系数b与阻抗参数值μ随之发生变化，使系统输出功率最大。

图10、图11为力-功率响应曲线，随磁化强度MA，MB的增加，非线性系数b值增大，功率响应变小，不稳定区域对应的激励幅值也变小；随阻抗参数μ的增大，功率响应幅值先增大后减小。

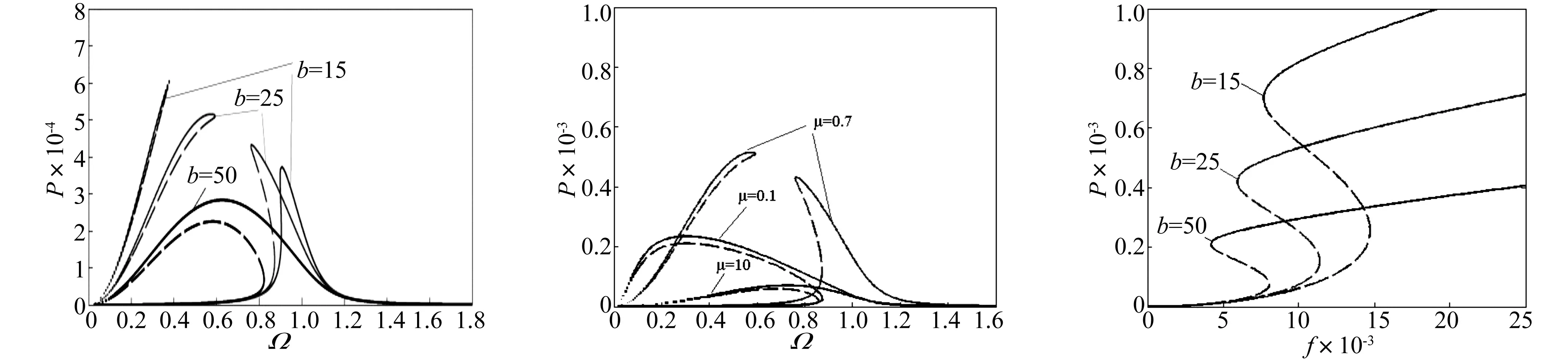
图8 功率频率响应曲线

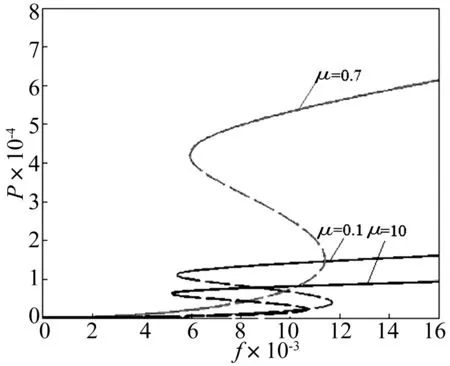
图11 力功率响应曲线

4 实验研究

双稳态压电发电系统实验原理见图12。将双稳态压电悬臂梁装置固定在激振台上，加速度传感器贴在压电悬臂梁自由端，利用激振控制器控制激励信号输出大小，用数据采集器采集实验数据。

不同激励幅值下系统输出电压频率响应曲线见图13，图中横轴为激励频率，纵轴为输出电压有效值。随激励幅值的增加，系统输出电压逐渐增加，且增加幅度逐渐变小，与图5力幅曲线趋势相同。1条曲线在一段较宽频率下系统输出电压较高，系统的解被吸引到高能量解时，系统输出电压也较高。

图12 实验原理图

不同频率下输出功率随电阻变化曲线见图14，随频率的增加，系统输出功率不断增加，频率为14Hz时输出功率最大；若继续增加频率，输出功率反会降低。对同一条随电阻变化功率曲线，存在的匹配电阻与激励频率无关，使输出功率最大。

5 结 论

利用谐波平衡法、实验方法研究双稳态压电发电系统响应特性。结论如下：

(1) 双稳态压电发电系统幅频响应曲线存在跳跃、多解现象。随非线性系数b的增加，不稳定区域范围增加，响应幅值先增加后减小，调节阻抗参数μ可使不稳定区域最小。

(2) 双稳态压电发电系统力幅响应曲线存在跳跃、多解现象。随非线性系数b的增加，响应幅值变小，不稳定区域对应的激励幅值也变小，调节阻抗参数μ可使不稳定区域最小。

(3) 通过调节磁化强度及负载阻抗可使系统输出功率最大。

参 考 文 献

[1]杜小振,褚金奎,朴相镐. 基于微型悬臂梁的发电机制探索[J]. 中国机械工程, 2005, 16(增): 41-43.

DU Xiao-zhen, ZHU Jin-kui, PIAO Xiang-gao. Study on electricity generating mechamism of micro cantilever[J].China Mechanical Engineering,2005, 16(S): 41-43.

[2]Ertrurk A,Inman D J. Broadband piezoelectric power generation on high-energy orbits of the bistable duffing oscillator with electromechanical coupling[J]. Journal of Sound and Vibration, 2011, 330(10): 2339-2353.

[3]Erturk A, Hoffmann J, Inman D J. A piezomagnetoelastic structure for broadband vibration energy harvesting[J]. Applied Physics Letters, 2009, 94: 254102.

[4]Moon F C,Holmes P J. A magnetoelastic strange attractor[J]. Journal of Sound and Vibration, 1979, 65: 275-296.

[5]Stanton S C, McGehee C C, Mann B P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator[J]. Physica D, 2010,239(10):640-653.

[6]And B,Baglio S, Trigona C, et al. Nonlinear mechnism in MEMS devices for energy harvesting applications[J]. Journal of Micromechanics and Microengineering, 2010, 20: 125020.

[7]Arrieta A F. Nonlinear dynamic response and modeling of a bistable composite plate for applications to adaptive structures[J]. Nonlinear Dynamics, 2009,58: 259-272.

[8]Arrieta A F, Hagedorn P, Erturk A,et al. A piezoelectric bistable plate for nonlinear broadband energy harvesting[J]. Applied Physics Letters, 2010, 97: 104102.

[9]Arrieta A F, Wagg D J, Neild S A. Dynamic snap-through for morphing of bi-stable composite plates[J]. Journal of Intelligent Material Systems and Structures, 2011,22: 103-112.

[10]孙 舒,曹树谦. 双稳态压电悬臂梁发电系统的动力学建模及分析[J]. 物理学报, 2012, 60(21): 103-114.

SUN Shu, CAO Shu-qian. Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system[J]. Acta Phys. Sinica, 2012, 60(21): 103-114.