应用改进复Morlet小波识别电力变压器绕组模态参数
2014-09-05王丰华廖天明金之俭
骆 波, 王丰华, 廖天明, 金之俭
(1. 上海交通大学 电气工程系,上海 200240; 2. 上海电力公司 运检部,上海 200240)
作为电力系统中重要组成部分,电力变压器的稳定性、可靠性与整个电网安全运行密切相关。统计分析表明[1],多数变压器故障来自绕组变形,而变压器绕组主要由线饼、绝缘垫块、压紧装置等构成,结构非常复杂,在变压器运行过程中发生的各种绕组变形故障均会使其机械特性改变、模态参数变化,导致变压器绕组振动特性及振动信号改变。因此,对绕组结构进行模态分析对其振动特性、故障诊断、动力特性优化设计及变形检测等具有重要意义及工程应用价值。
变压器绕组模态参数主要包括固有频率、振型、阻尼比等,能全面描述整个绕组机械系统固有动态特性,物理意义较明确。目前,获取变压器绕组类机械结构模态参数途径主要依赖绕组结构的试验测试,进而分析与参数识别。传统模态参数识别方法主要包括最小二乘负指数法、时间序列分析法等时域辨识方法[2]及最小二乘圆拟合法、分区模态综合法、频域总体识别法[3]等两类。但此方法大多限于时域或频域中单独对测试信号进行识别,参数辨识精度有限;而且对测试信号中噪声较敏感,固有频率识别与定阶存在较大主观性。因此,对电力变压器绕组类结构复杂强非线性机械结构系统而言,需寻求新的模态参数识别方法以提高模态参数识别准确性,此亦为变压器绕组结构健康监测的重要前提。
小波变换法因时频局部化特性良好、可使多自由度系统模态自动解耦等特点被广泛用于结构模态参数识别领域[4]。但在电力变压器绕组类机械结构系统模态参数识别领域鲜有应用。故本文以某10 kV电力变压器绕组为研究对象,尝试用复Morlet小波变换法对绕组轴向激振实验振动响应信号进行时频分析,用改进Crazy Climber算法提取小波脊线,以期获得较准确、高效的模态参数识别结果。为说明计算结果的正确性,本文给出使用多参考最小二乘复频域法PolyMAX法获所得绕组模态参数识别结果。
1 理论基础
1.1 小波变换与小波脊
对任意信号x(t)∈L2(R),其连续小波变换为:
(1)
式中:a,b为尺度因子、平移变量;ψ*表示共轭。
本文采用复Morlet小波作为母小波,原因为[5]:① 该小波的实部、虚部幅值均为按指数衰减的简谐振动信号,与动态系统自由响应信号一致;② 该小波具有单值频率,若分析信号与某尺度小波高度相关,即在该尺度下小波系数较大,则小波频率可表征产生该响应信号的动态系统固有频率。因此对密集模态的识别效果较好。Morlet小波时频域定义为:
(2)
(3)
式中:ω0为Morlet小波中心角频率。
由式(2)、(3)可见,Morlet小波的时、频域波形均为高斯窗函数形式,已具备分离出各阶模态能力。对形如x(t)=A(t)cos(ωt)的渐进单频信号进行Morlet小波变换有:
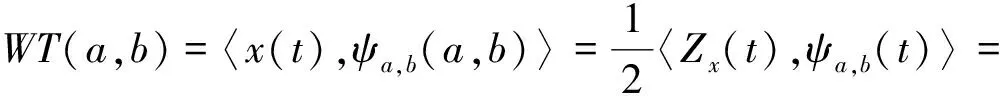
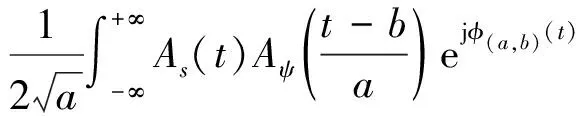
(4)
式中:Zx(t)为信x(t)的解析形式;ψa,b(a,b)为母小波;φ(a,b)(t)为相位。分别表示为:
Zx(t)=x(t)+jH[x(t)]=As(t)ejφ(t)
(5)
ψa,b(a,b)=Aψ(t)ejθ(t)
(6)
(7)
定义使φ′(x)=0且φ″(x)≠0的点x=x0称为φ(x)=0的一阶平稳相位点[6]。在小波变换域平面内,若平稳相位点t(a,b)满足条件t(a,b)=b,则定义满足条件的点(a,b)为小波变换脊点,脊点集合称为小波变换脊线。
若t=t0为一阶平稳点,则对式(7)求导有:
(8)
令a=ar(b)为小波脊线,将t0=b代入上式有:
(9)
令φ′(b)=ωs(b),据式(9)得信号在时间b处频率ωs(b)为[5]:
(10)
由上式可见,信号x(t)在时间b处频率与小波在尺度a=ar(b)处值有对应的定量关系。因此,只要获得小波变换脊线所在尺度位置即可求出原信号在该处频率特性。与小波脊对应的小波系数连线WTs(ar(b),b)称为小波骨架,其实部对应信号本身[7]。
1.2 模态参数识别方法
单自由度线性系统自由振动运动微分方程解的形式为[6]:
x(t)=Ae-εωntsin(ωdt+η)
(11)
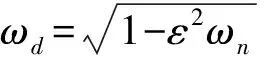
对式(11)进行小波变换:
(12)
将上式在t=b处进行Taylor级数展开:
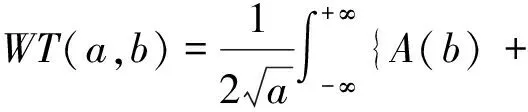

(13)
忽略高阶分量,上式可近似为:
(14)
选择Morlet小波为母小波,将式(2)、(12)代入式(15)得自由衰减振动信号x(t)的Morlet小波变换:
(15)
得小波系数模值为:
(16)
当尺度a=ω0/ωd时,小波系数模取得极大值,幅值、相位分别为:
(17)
∠WT(a,b)=ωdb+η
(18)
a=ω0/ωd确定的尺度值为该小波变换的一阶平稳点,因此可由小波脊线提取方法获得与该尺度位置对应的固有频率。此时尺度a对应频率即为系统固有频率。而该尺度下小波系数模值对数对时间的斜率即为无阻尼固有频率ωn与阻尼比ε的乘积,设斜率为k1,固有频率为fk,则得系统在该阶固有频率下阻尼比:
ε=-k1/(2πfk)
(19)
由此可见,对系统自由振动信号进行小波变换后,提取小波脊线的尺度位置即可识别出系统该阶固有频率及阻尼比。对多自由度系统,由于小波变换过程实为信号分解过程,只在子小波定义的窗内对信号进行分解。在窗外,因小波具有快速衰减特性,几乎不分解信号,此时小波变换过程即为时频滤波器对信号带通滤波。对特定频率尺度a,只有与该参数对应的模态频率成分信号才能通过小波滤波器,其它频率信号对此阶信号影响可忽略不计。故多自由度系统可变为单自由度系统分析[9]。
小波变换识别模态参数算法的输入应为系统按指数衰减的正弦自由振动信号。而变压器绕组轴向激振实验中采集的振动信号为白噪声激励下受迫振动,可通过计算系统频响函数,获得系统脉冲响应函数:
(20)
式中:X(jω)为信号x(t)傅氏变换;Y(jω)为实验中所采信号傅氏变换。由于系统脉冲响应函数h(t)即为频响函数H(jω)的傅里叶逆变换,而脉冲响应函数为系统自由振动信号,满足小波算法的输入要求。
1.3 基于改进Crazy Climber 算法的小波脊线提取
小波变换模态参数识别方法关键为小波脊线的提取。目前该提取方法主要有按定义计算的相位法及模值法、改进的局部模极大值法等[10]。但均存在对信号噪声较敏感、不能有效提取多条脊线等问题。因此,为能在噪声环境下准确进行多阶模态参数识别,本文引入自适应优化思想到Crazy Climber算法[11]中,完成复Morlet小波变换系数矩阵中小波脊线的提取。设信号经小波变换后时频矩阵为B×A矩阵,矩阵中每点(i,j)的小波变换系数值为M(i,j)。则据Crazy Climber算法提取小波脊线的基本过程为:
(1) 初始化N个可移动爬升点、小波变换视频矩阵尺寸相同爬升点观测矩阵B及度量矩阵D,并将N个可移动爬升点均匀分布于时频空间,度量矩阵D及观测矩阵B初始化为零矩阵;
(2) 定义系统循环参量T0=max(M)-min(M),并令系统当前循环参量为Tt=T0,记录可移动爬升点初始位置为Bk(t)=(i,j),k∈[1,2,…,N];
(3) 在t时刻,设可移动爬升点对应位置为Bk(t)=(i,j)。t+1时刻,在不考虑边界点时,可移动爬升点对应位置Bk(t+1)=(i′,j′)确定规则为:①t时刻i值,按50%概率左移或右移一格,即i′=i-1或i′=i+1;②t时刻j值,按50%概率上移或下移一格,即j′=j-1或j′=j+1;若小波变换系数矩阵M(i′,j′)>M(i,j),则该点垂直移动,有Bk(t+1)=(i′,j′),否则该点按概率p沿垂直方向移动,即Bk(t+1)=(i′,j′),按概率1-po沿垂直方向不移动,即j′=j,Bk(t+1)=(i′,j′),概率p的计算公式为:
(21)
(4) 移动结束后,在度量矩阵D的相应位置(i′,j′)上增加度量值M(i′,j′);
(5) 重复步骤(3)、(4),直至系统当前循环变量低于设定阈值Tf;
(6) 设定合适密度阈值Td,对最终所得度量矩阵D进行筛选低于该阈值的矩阵元素置零,此为降低信号中噪声对计算结果影响、提高模态参数识别精度之关键;
(7) 据所得度量矩阵D在时间方向(j向)进行递归,给定任意点(i,j),在(i-Δi,j)、(i-Δi,j±Δj)中寻找最优相邻点,并形成一条脊线;
(8) 重复步骤(7),直至所有满足要求的点均在脊线中,形成整个时频平面的脊线。
(1)~(6)步为随机移动阶段,(7)~(8)步为链接递归阶段。在脊线链接递归阶段,遍历网格大小选取直接影响小波脊线提取后形态。网格越小,提取脊线越平滑,模态参数辨识结果亦更准确。而网格大小亦直接影响密度阈值Td的选取,为保证脊线提取效果及模态参数识别精度,本文引入自适应优化算法确定密度阈值及网格尺寸的选取。过程为:① 在链接递归初始阶段,引入脊线参量s为一设定常数,其含义为所需提取的小波脊线数量。② 在链接递归过程中,将密度阈值Td设为相对较小数值,以确保真实模态能被识别。当一次脊线提取完后对模态数量进行统计,若超过脊线参量s,则增加密度阈值Td的数值,继续循环该过程直至提取的脊线数量与模态参量一致;否则减小密度阈值Td的数值,继续循环该过程直至提取的脊线数量与模态参量一致。在算法随机移动过程较充分情况下,该自适应过程可取得较理想结果。
2 仿真分析
为说明所提结合改进Crazy Climber算法复Morlet小波变换进行信号处理及模态识别的优越性,构造自由衰减仿真信号为:
x(t)=eε1ωn1πtsin(ωd1t)+
eε2ωn2πtsin(ωd2t+θ)
(22)
式中:ωd1≈ωn1=160π;ωd2≈ωn2=220π;ε1=-0.13;ε2=-0.08;t为时间;采样频率256 Hz,采样时间1 s。为说明信号中噪声对用Crazy Climber算法提取小波脊线影响,在式(22)中加入信噪比SNR=-3 dB的白噪声。
图1为信号x(t)时域波形。图2为采用复Morlet小波与原Crazy Climber算法所得小波脊线。由两图看出,信号x(t)的两个频率分量分别在80 Hz及110 Hz附近,即式(22)仿真信号中的频率分量。说明用复Morlet小波与Crazy Climber算法计算结果的正确性。但在原始信号中加入信号比为SNR=-3 dB的白噪声后,提取的小波脊线尤其110 Hz频率分量对应的小波脊线出现弯曲现象,说明信号中的噪声对原Crazy Climber算法的小波脊线提取结果有影响。

图1 信号x(t)的时域波形
用改进Crazy Climber算法对加入信号比SNR= -3 dB白噪声的仿真信号进行小波脊线提取后计算结果见图3。由3图看出,小波脊线弯曲现象已消失,表明本文改进Crazy Climber算法的有效性。
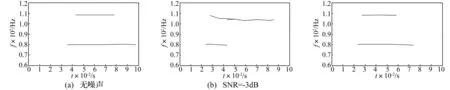
图2 用Crazy Climber算法所得小波脊线图
3 变压器绕组轴向激振实验分析
3.1 变压器绕组轴向激振实验描述
实验对象为一台饼式绕组结构10 kV变压器。用三维振动加速度测试振动信号,测点布置实物见图4。试验时用电磁激振器对绕组进行轴向激振,激振位置见图5。所用激振信号为白噪声信号,带宽20 kHz。白噪声信号发生器经功率放大直接驱动电磁激振器对变压器绕组进行激振。用DH5922振动信号采集与分析系统拾取各测点加速度传感器振动信号,获得绕组综合频响函数。

图4 绕组测点布置图
3.2 结果与分析
图6为根据变压器绕组轴向激振实验所得变压器绕组振动频响函数(Frequency Response Function, FRF),用半对数坐标表示。由图6看出,频响函数在229 Hz,322 Hz,425 Hz,724 Hz左右有明显叠加峰值结果。对其进行傅里叶逆变换,获得自由振动信号见图7。
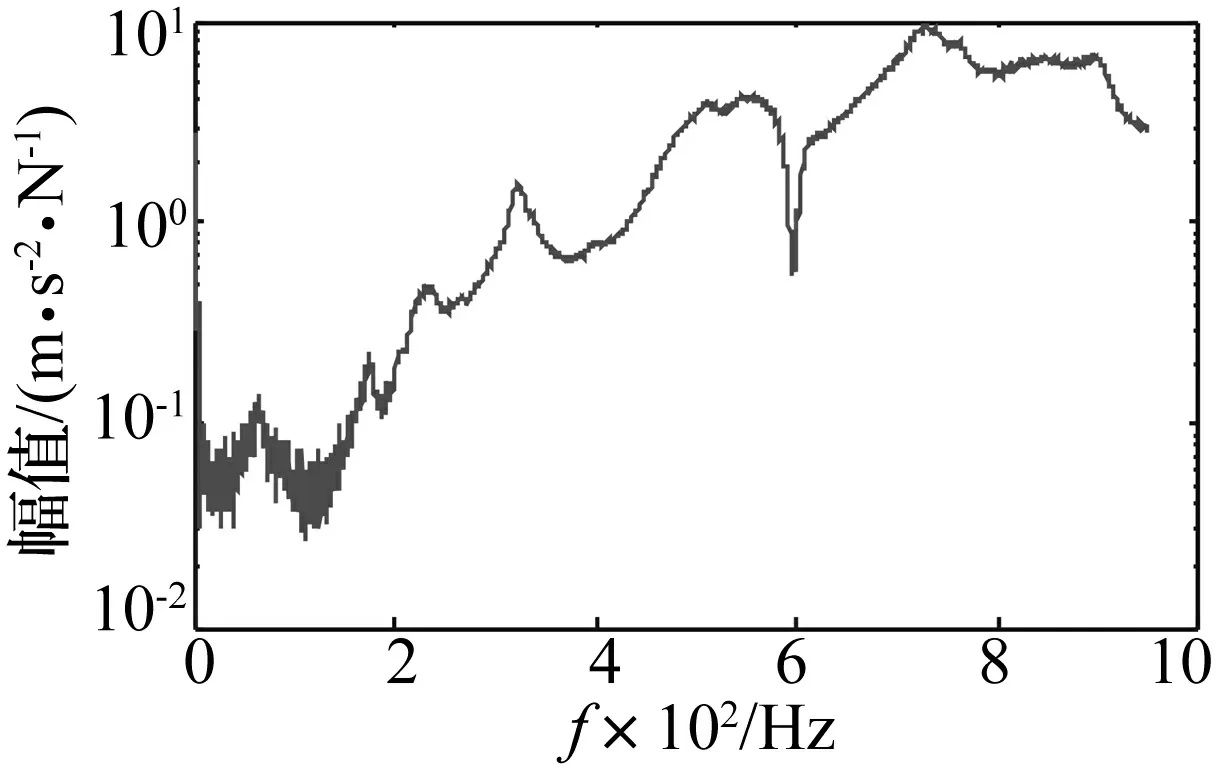
图6 振动频响函数

图7 自由振动时域信号
选复Morlet小波为小波母函数,对图7的自由振动信号进行连续小波变换,获得小波变换时频见图8。由图8看出,小波变换已将各阶固有频率所在频带清晰分离。但仅由时频图较难获得精确固有频率,需进一步提取小波脊。图9为用Crazy Climber算法据图8小波变换结果中提取的小波脊线图。由图9看出,绕组前四阶固有频率分别为227 Hz,330 Hz,427 Hz,732 Hz。分别提取四频率处小波系数,据式(19)得阻尼比分别为4.71%,4.47%,4.97%,3.05%。
为说明用复小波变换识别模态参数结果的正确性,本文亦用PolyMAX方法对测试所得振动数据模态参数进行识别[12]。表1为两种方法计算结果。由表1看出,两种方法对绕组固有频率识别一致性良好,说明用复小波变换法识别的绕组模态参数的正确性。此外,据PolyMAX方法计算所得各阶固有频率阻尼比差别较大,尤其二阶固有频率对应阻尼明显小于其它各阶,此由于PolyMax法对频响函数拟合时噪声影响所致。可见PolyMax在识别过程中受振动噪声影响较大。当频响函数存在较大噪声时,PolyMax计算结果对频率拟合范围较敏感,需根据频响函数峰值预先确定拟合区间而存在较大主观性。因此,基于小波变换的模态识别方法在变压器绕组模态识别中抗干扰性更好、识别精度更高。
4 结 论
(1) 本文根据实体变压器绕组轴向激振实验测试结果,提出用复Morlet小波变换及改进Crazy Climber算法对变压器绕组模态参数进行识别。计算结果与用PolyMAX方法识别结果的良好吻合说明该方法的正确性。变压器绕组前四阶固有频率均远离100 Hz电动力激励频率,说明变压器绕组结构设计较合理。
(2) 本文所提复Morlet小波变换及改进Crazy Climber算法在变压器绕组类复杂结构模态参数识别中优势明显、识别精度高、抗干扰性能强,且能清晰刻画信号能量随时间频率分布。研究结果可为变压器绕组结构振动特性分析及基于振动分析法的变压器绕组状态监测提供依据。
参 考 文 献
[1]金文龙,陈建华,李光范,等.全国110 kV及以上等级电力变压器短路损坏事故统计分析[J]. 电网技术,1999,23(6):21-25.
JIN Wen-long, CHEN Jian-hua, LI Guang-fan,et al. Statistics and analysis on power transformer damage caused by short circuit fault in 110kV and higher voltage classes[J]. Power System Technology, 1999,23(6):21-25.
[2]林循泓,潘得引,臧朝平,等,振动模态参数识别及其应用[M].南京:东南大学出版社,1994.
[3]周 云,易伟建.用PolyMAX方法进行弹性地基板的实验模态分析[J].振动与冲击,2007,26(7):139-145.
ZHOU Yun,YI Wei-jian.Experimental modal analysis of a slab on elastic foundation by PolyMAX method[J].Journal of Vibration and Shock, 2007, 26(7):139-145.
[4]何启源,汤宝平,程发斌. 基于修正Morlet小波的自适应模态参数识别[J]. 中国机械工程,2007,18(20): 2476-2480.
HE Qi-yuan,TANG Bao-ping,CHENG Fa-bin. Modified Morlet wavelet-based adaptive modal parameter identification[J]. China Mechanical Engineering, 2007,18(20): 2476-2480.
[5]孙 鹏,丁幼亮,张劲泉,等. 基于Morlet小波变换的结构密集模态参数识别[J]. 东南大学学报,2012,42(2):339-345.
SUN Peng, DING You-liang, ZHANG Jin-quan,et al. Modal identification of closely spaced modes based on Morlet wavelet transform[J]. Journal of Southeast University,2012,42(2):339-345.
[6]刘 宁. 系统模态参数小波辨识方法研究[D].天津:天津大学,2006.
[7]伊廷华,李宏男,王国新.基于小波变换的结构模态参数识别[J].振动工程学报, 2006,19(1):51-56.
YI Ting-hua,LI Hong-nan,WANG Guo-xin. Structural modal parameter identification based on wavelet transform[J].Journal of Vibration Engineering, 2006,19(1):51-56.
[8]Lardies J, Ta M N, Berthiller M. Modal parameter estimation based on the wavelet transform of output data[J]. Archive of Applied Mechanics, 2004, 73(9-10): 718-733.
[9]罗光坤,张令弥. 基于Morlet小波变换的模态参数识别研究[J].振动与冲击,2007,26(7):135-139.
LUO Guang-kun, ZHANG Ling-mi.Study on identification of modal parameters based on Morlet wavelet transformation[J]. Journal of Vibration and Shock, 2007, 26(7):135-139.
[10]Carmona R, Hwang W L. Characterization of signals by the ridges of their wavelet transforms[J].IEEE Transactions on Signal Proeessing,1997,45(10):2586-2590.
[11]Carmona R, Hwang W L, Torresani B. Multi-ridge detection and time-frequency reconstruction[J].IEEE Transactions on Signal Processing,1999, 47:480-492.
[12]谢小平,韩 旭,吴长德,等,基于PolyMAX方法的某轿车车身实验模态分析[J]. 汽车工程,2009,31(5):440-444.
XIE Xiao-ping, HAN Xu, WU Chang-de,et al.Experimental modal analysis for a car Body-in-white based on PolyMAX method [J].Automotive Engineering, 2009, 31(5): 440-444.
