基于饱和补偿控制器的壁板结构振动控制

马天兵， 杜 菲

(安徽理工大学 机械工程学院，安徽 淮南 232001)

虽加筋壁板结构非线性振动问题得以广泛研究[1-2]，而涉及结构振动控制的研究较少。MCS算法因不需精确的数学模型且在非线性扰动情况下具有良好的闭环鲁棒性[3-4]被应用于土木结构振动控制中[5-6]。但标准的MCS算法在快速扰动下无法保证系统稳定[7]，故带积分及sign函数补偿的EMCS算法[8]已被应用于非线性混沌系统中。由于仿真实验中发现因其正积分环节及sign函数在±1间高频切换影响，导致EMCS算法控制器输出易出现饱和现象，影响振动控制效果。因此本文基于波波夫准则设计新的饱和补偿器，针对飞机壁板前二阶模态，施加正弦叠加随机复合扰动。仿真及实验结果表明，该方法能保留EMCS算法的自适应跟踪特性，使控制器输出快速脱离饱和区，并在复合扰动下前二阶模态分别达31.79 dB，9.52 dB的振动控制效果。

1 SCMCS算法原理

标准的MCS算法控制律u表达式为[3]：

u(t)=K(t)Xp(t)+Kr(t)r(t)

(1)

式中：r(t)为参考输入；K(t)，Kr(t)为自适应结构调整增益，计算式为：

(2)

式中：α，β为决定自适应效果的正加权系数值；ye(t)为输出误差信号；e(t)为状态误差信号，计算式为：

e(t)=Xm(t)-Xp(t)

(3)

ye(t)=Cee(t)=Ce[Xm(t)-Xp(t)]

(4)

Ce=[0 1]P

(5)

其中：Xm(t)，Xp(t)分别为参考模型与被控对象状态变量。

(6)

式中：Am为参考模型系数矩阵；P，S为正定阵。

为解决快速扰动下标准MCS算法的稳定性问题，文献[8]提出改进的EMCS算法，表达式为：

u(t)=K(t)Xp(t)+Kr(t)r(t)+

KN(t)sign(ye(t))

(7)

实验中证明在求解器中因KN(t)不断正向累积、sign函数高频切换导致控制器较易进入饱和区。为避免此情况，本文用恒定正常数取代KN(t)，用erf高斯误差函数取代sign函数，降低补偿器的累加速率，促使自适应控制器难以进入非线性饱和区。高斯误差函数值域为(-1,1)，表达式为：

(8)

含饱和补偿的SCMCS算法为：

u(t)=K(t)Xp(t)+Kr(t)r(t)+ρerf[ye(t)]

(9)

其中：ρ为一正值，由实验过程中试凑获得。

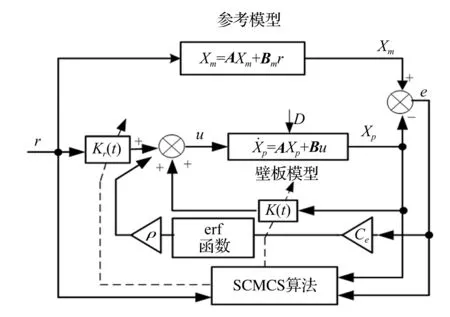
图1 SCMCS算法控制原理图

SCMCS算法控制原理见图1。图1中D为外部扰动；A，B为壁板模型系数矩阵；Am,Bm为参考模型系数矩阵。

2 稳定性证明

非线性控制器设计通常以超稳定性理论为基础[9]，借鉴文献[9]方法，通过波波夫准则验证SCMCS算法的稳定性。

(10)

(11)

BKr(t)]r(t)-[Bρerf(ye)+D(Xp,t)]

(12)

(13)

其中：

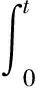
设A,B随时间的变化速度远慢于自适应系数变化速度，b，d为B,D矩阵最末位元素，则：

(14)

(15)

(16)

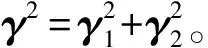
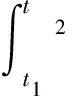
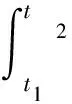
(19)

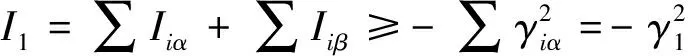
(20)

由于dye(t)有界，ye(t)(bρerf[ye(t)]为非负， 故：

(21)

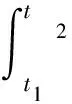
d+bρerf[ye(t)]dt≥-γ2

(22)

由此可据波波夫准则判断SCMCS算法在非线性扰动情况下具有全局渐进稳定性。

3 仿真验证

3.1 模型参数确定

3.2 仿真结果与分析

整个仿真时间设2 s，持续激励时间为1 s，然后自由衰减， 激励信号为结构前两阶模态频率为基准频率的正弦信号及频带20～500 Hz的随机信号混合。幅值均为5 V(功放输入端电压值)，设控制器饱和电压15 V，α=0.1,β=0.01,τ=ρ=10。定义不加限幅设计的EMCS算法为EMCS1，加限幅设计但未考虑饱和补偿的EMCS算法为EMCS2，本文改进方法为SCMCS。由控制电压、自适应系数及跟踪误差等比较不同方法效果。见图2～图7。

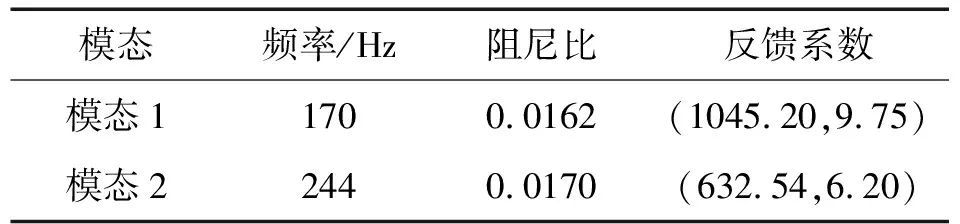
表1 系统参数

图2 第一阶模态控制电压

图5 自适应速度反馈系数

由图2～图7看出：不考虑限幅的EMCS1算法较易发散。实际上，诸多控制器硬件(如DSPACE系统) 输出端口电压均有相应限制，须在软件算法中施加限幅功能。施加限幅功能后EMCS2算法较快进入饱和截止状态。但控制器一旦进入饱和区，控制效果则明显下降，甚至影响系统的稳定性。本文设计的含饱和补偿的SCMCS算法不断调节自适应控制律，使其快速脱离非线性饱和区，收敛性、跟踪效果较好，可有效克服EMCS算法中补偿器不断累加所致不利影响。

4 实验验证

实验装置(图8)由计算机、DSPACE系统、ARJ21型飞机壁板、HEA-200D型功放、泰克示波器及压电片组成。通过敲击法识别壁板振型，将压电片贴在被控模态应变最大处，压电作动器1、2分别控制一、二阶模态。由DSPACE的AI口采集压电传感片电压信号，在SIMULINK中编写算法程序并下载至DSPACE中，再由AO口输出不同控制电压抑制各阶模态振动。为充分激励被控模态，接入电压功放输入端电压(激励信号)分别为信号叠加：第一阶正弦信号，幅值7 V，频率170 Hz；第二阶正弦信号，幅值2 V，频率244 Hz；随机噪声幅值-4～+4 V，带宽50～500 Hz。见图9～图12。图9、图10显示采用EMCS算法控制时，控制器耦合较多高频分量，导致压电传感片输出信号呈现高频振荡现象，控制器较快进入饱和截止状态，主要由补偿器中积分因子及sign函数共同作用所致。图11显示本文所提SCMCS算法对复合扰动下壁板前两阶模态振幅分别达到31.79 dB 及9.52 dB 的抑制效果。而第一阶模态控制效果明显好于第二阶，原因在于因壁板筋条的存在导致结构出现局部模态及整体模态，第一阶模态属局部模态，较易控制，而第二阶模态为整体模态，较难控。由图12看出，第二阶模态的控制电压小于第一阶，所产生作用力也较小，一定程度上影响控制效果。

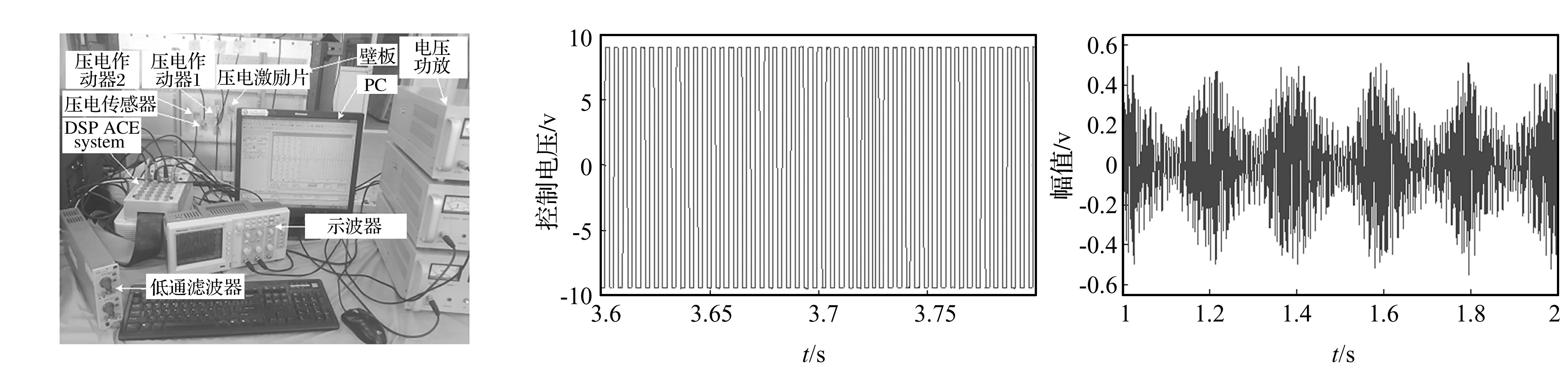
图8 振动控制实验照片

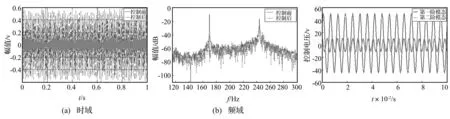
图11 SCMCS算法振动控制效果

5 结 论

本文针对EMCS算法控制器的输出饱和问题，基于波波夫准则提出新的具有饱和补偿功能的SCMCS算法，并应用于壁板结构振动控制中。通过正弦复合随机扰动激励实验表明，该方法对壁板前两阶模态振动具有较好控制效果，能有效克服EMCS算法中控制器饱和现象、改善控制器性能、提高系统稳定性。

参 考 文 献

[1]Srivastavaa A K L. Dynamic instability of stiffened plate subjected to non-uniform harmonic in-plan edge Loading[J].Journal of Sound and Vibration , 2003, 262 (5): 1171-1189.

[2]吴 晓.复合材料层合矩形板非线性湿热振动[J].振动与冲击,2002,21 (1):27-29.

WU Xiao. The nonlinear moist thermal vibration of composite materials laminates rectangular plates[J]. Journal of Vibration and Shock, 2002,21(1):27-29.

[3]Stoten D P, Benchoubane H. Robustness of a minimal controller synthesis algorithm[J]. Int.J. Control,1990, 51(4):851-861.

[4]Stoten D P, Benchoubane H. The extended minimal controller synthesis algorithm[J]. Int.J. Control,1992, 56(5):1139-1165.

[5]瞿伟廉,查小鹏．基于最小控制综合算法的结构振动控制研究[J]．武汉理工大学学报,2007,29(1):145-148．

QU Wei-lian，ZHA Xiao-peng. Application of minimal control synthesis algorithm to structural vibration control[J].Journal of Wuhan University of Technology,2007,29(1): 145-148.

[6]张凯静,周莉萍,王官磊.最小控制合成算法在结构振动控制中的应用[J].华中科技大学学报(城市科学版),2010,27(3):76-80.

ZHANG Kai-jing,ZHOU Li-ping,WANG Guan-lei. Minimal control synthesis algorithm in structural vibration control[J].J. of HUST.(Urban Science Editon),2010,27(3): 76-80.

[7]Bernardo M di, Stoten D P. A new extended minimal control synthesis algorithm with an application to the control of chaotic systems[C]. Proceedings of the 36th Conference on Decision & Control, 1997:1902-1907.

[8]Bernardo M di, Stoten D P. Minimal control synthesis adaptive control of chaos nonlinear systems: utilizing the properties of chaos.phil[J]. Trans.R.Soc.A, 2006,364(9): 2397-2415.

[9]马天兵,裘进浩,季宏丽.用于壁板结构多模态振动主动控制的改进最小控制合成(MCS)算法[J].西安交通大学学报,2012, 46(7) :87-92.

MA Tian-bing, QIU Jin-hao, JI Hong-li. Improved minmal control synthesis(mcs) algorithm for multi-modal active vibration control of piezoelectric panel structure[J].Journal of XI’AN Jiaotong University, 2012, 46(7) :87-92.