柴油机振动信号盲分离组合算法
2014-09-05韩春杨姚国凤张修路
韩春杨, 姚国凤, 赵 建, 张修路, 盛 鑫
(1.吉林大学 机械科学与工程学院工程力学系,长春 130022;2.汽车振动噪声与安全控制综合技术国家重点实验室,长春 130011)
机械系统振动信号为故障特征识别与诊断的重要信息来源。由于机械系统滤波、耦合作用[1-2]使其信号具有非平稳性,且在时、频域上有大量重叠,因此限制了一些时频分析手段分析机械系统振动信号的能力。而盲源分离法(BSS)可在输入源及混合系统均未知时,假设输入源相互统计独立,利用输出源对输入源进行估计[3-6];或假设源信号部分子带相互统计独立,并基于小波包分解对输入源进行盲源分离[7]。
近年来盲源分离方法在机械系统信号处理方面取得诸多进展,但由于大多数机械系统振动信号混合模型均为卷积模型、机械系统盲振动源数量未知,如旋转机械系统所含大量盲振动源使在医学信号处理、混合语音信号分离、图像信号消噪等应用[8-9]较好的盲源分离算法在机械系统混合信号分离上遇到困难。
本文在已有研究基础上,提出多通道盲最小均方差(Multi-Channel Blind Least Mean Squares,MBLMS)与缩减盲源(The Deflation Source,TDS)结合的盲源分离组合算法,一定程度上可解决上述存在问题,并由模拟的混合振动信号盲去卷积及柴油机燃烧激励、活塞撞击缸体激励的盲识别两方面验证该算法的有效性。
1 机械系统振动特性分析
机械系统(如柴油机、变速箱)可分解成大量子结构系统,由于完整机械系统会有较多固有频率,加之该系统激励源数量较大,且部分激励源为非周期性激励,因此,机械系统响应较复杂。一个机械系统可近似视为n的自由度振动系统,任意激励力系统受迫振动方程为:
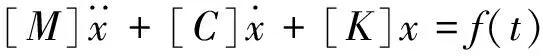
(1)
其中:[M],[C],[K]分别为n×n阶质量阵、刚度阵、阻尼阵;f(t)=[f1(t),f2(t),…,fn(t)]T为时间任意函数。
利用模态叠加法对式(1)解耦,得此系统脉冲响应矩阵为:
[hij(t)]=φHp(t)φT
(2)
其中:hij(t)为沿第i质量块单位脉冲激励引起的第i个质量块暂态响应;φ为n×p截断模态矩阵;Hp(t)=diag[h1(t),h2(t),…,hp(t)];hj(t)(j=1,2,…,p)为各主坐标脉冲响应函数。
综上知,在材料的弹性形变范围内,机械振动系统响应可表示为脉冲响应阵与任意激励力卷积效果及瞬时作用效果的和:
(3)
其中:xi(t)为第i个自由度位移响应;fj(t)为非周期激励力;Vj为瞬态冲击激励幅值;ni(t)为高斯白噪声。
2 多通道盲最小均方差与缩减盲源组合(MBLMS-TDS)算法
由于脉冲响应与任意激励力瞬时作用效果可表示为卷积的特例,因此多个激励力引起的机械系统振动响应为:
Y=H*S
(4)
其中:S=[s1(t),s2(t),…,sm(t)]T为输入系统m个源向量;Y=[y1(t),y2(t),…,yn(t)]T为系统输出n个观察信号;H=[hij]n×m为混合系统脉冲响应矩阵;*表示卷积。
由于上述卷积模型的存在,以往大部分仅针对瞬态混合模型的盲源分离算法具有一定局限性。本文采用多通道盲最小均方差与缩减盲源组合(MBLMS-TDS)算法对多通道卷积模型进行盲解卷积。盲解卷积目的为估计一个解混系统W,使观察信号Y(t)经解混系统W所得Y为源信号S的较好估计。解混系统模型为:
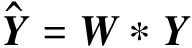
(5)
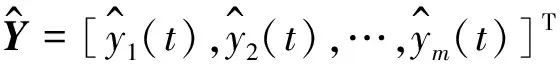
2.1 多通道盲最小均方差(MBLMS)
MBLMS方法为根据中心极限定理,通过散度(Kullback-Leibler Divergence)对估计源信号进行非高斯性度量,利用相对熵[10]构造多通道目标函数表达式:
(6)
由于式(6)对概率密度函数估计较困难,因此用Gray’s变量准则[11]取代式(4)得:
(7)
其中:α为参数,可据源信号统计分布特性选取,源信号为超高斯分布时,α=1;源信号为亚高斯分布时,α=4。
求目标函数最值,寻找自适应性算法:
(8)
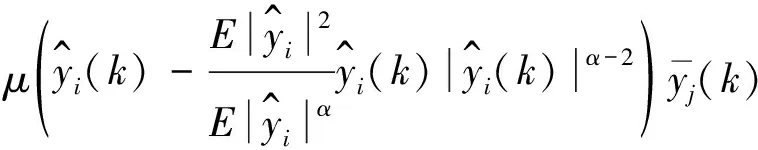
(9)
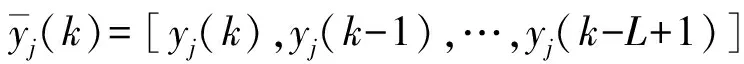
由此知,在源信号数量未知时能分离出具有超高斯性或亚高斯性的源信号;但用MBLMS算法仅能分离出一个盲源。
2.2 缩减盲源方法(TDS)
由于源信号统计的独立性及线性时不变滤波器性质可知,输出混合信号向量Y的能量总和为:
(10)
其中:E为期望。

(11)
y1j(k)=yj(k)-w1j*y1(k)
(12)
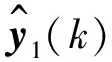
3 模拟示例

图1 初始激励源信号
用MBLMS-TDS算法对以上三盲源进行盲解卷积,见图4,α=1时,稀疏脉冲响应激励源s3经盲解卷积系统被分离出来;α=4时,用MBLMS-TDS算法依次从混合观察源信号中分离出归一化均匀分布激励源s1与正弦波激励源s2。将混合前三激励源x1,x2,x3与经盲解卷积分离出来的激励源s1,s2,s3比较知,除存在顺序、幅值的不确定性外,s1,s2,s3带有精度范围内误差,说明MBLMS-TDS算法能成功对混合源信号进行盲解卷积,且能分离出多个盲源。

图4 分离信号
4 柴油机表面振动加速度信号高斯性研究
用MBLMS-TDS算法对混合源信号分离时,源信号间应统计独立,各源信号分量均为非高斯分布或至多有一个分量服从高斯分布。因此,在分离前应对柴油机表面振动加速度信号进行非高斯性研究。图5为由某型号柴油机表面测得的50组振动加速度信号分别计算的四阶累计峰度(kurtosis)值。由图5看出, 50组振动加速度信号的kurtosis值均大于零。因此,振动加速度信号可认为服从超高斯分布。表明可用MBLMS-TDS算法对振动加速度信号进行分离。
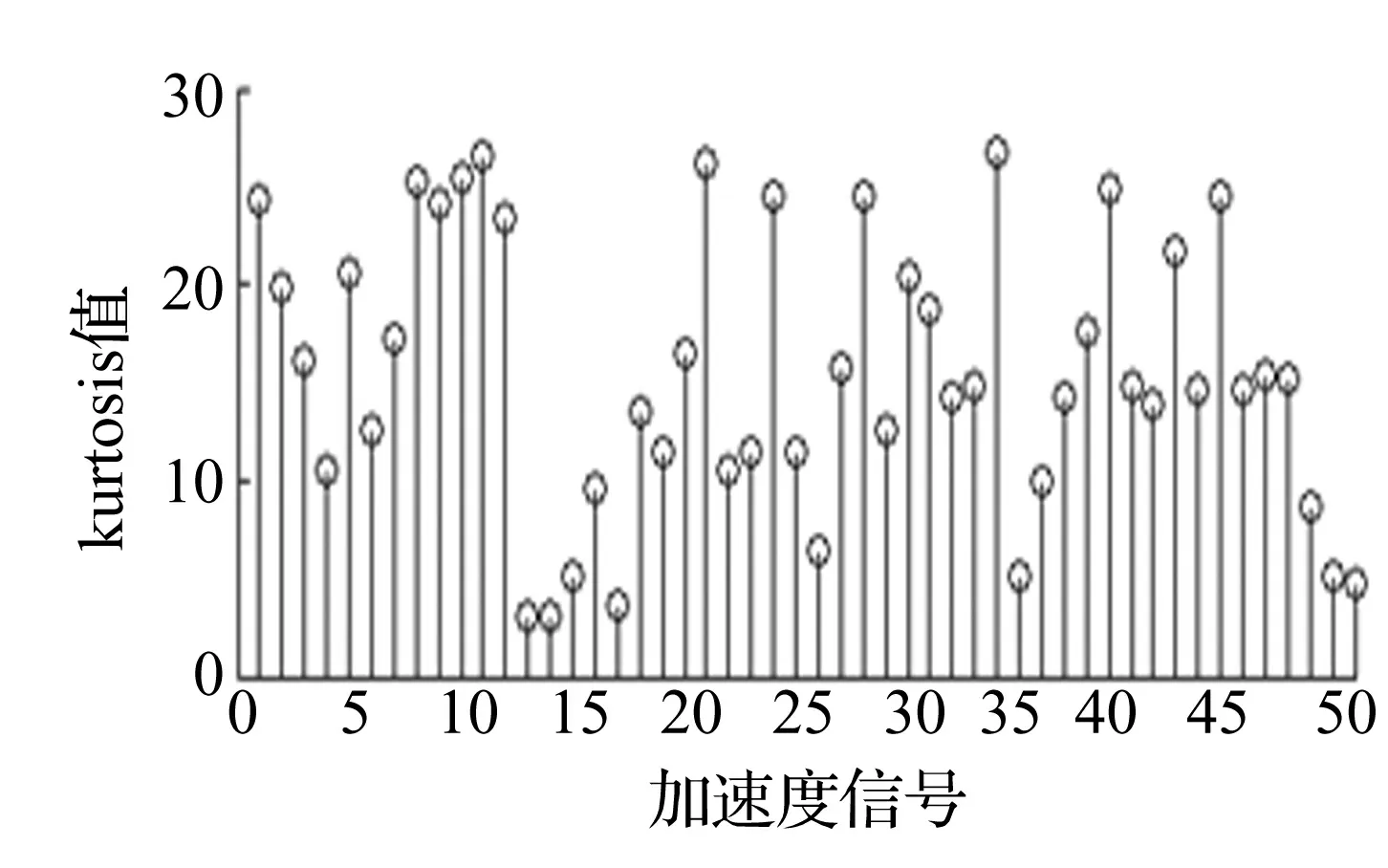
图5 加速度信号kurtosis值
5 柴油机振动信号盲解卷积
用MBLMS-TDS算法对柴油机表面振动加速度信号进行盲分离。观测信号源于一汽技术中心某型号四缸柴油机,在#1缸中插入型号为6052A的Kistler爆发压力传感器,其灵敏度为-20 PC/bar。并在其一侧曲轴转角0°~180°范围布置10个B&K公司型号为33B30的振动加速度传感器。缸盖顶端均匀布置2测点,传感器方向为Z向,缸盖测端及缸体侧面均匀布置6测点,传感器方向为Y向,油底壳测端、低端各布置1个测点,传感器方向为Y,Z向。
在上止点(TDC)附近短时间内振动辐射噪声主要由缸体振动产生,其中缸体振动主要激励源为燃烧、活塞撞击缸体及其它微弱振动激励力组成。燃烧激励主要由气体压缩、膨胀及爆燃组成,其对缸体冲击力称为缸内燃烧压力。假设内燃机各种激励为严格的周期信号,且在上止点(TDC)附近短时间内振动系统为时不变[13]。
进行振动信号测量试验在全消声室内进行,背景噪声30 dB,柴油机进排气噪声用长管引出。柴油机工况为全载荷,转数为2 500 r/min,柴油机发火顺序1-3-4-2。由上止点(TDC)附近所测柴油机表面振动加速度信号中选4个具有较大振幅信号x1,x2,x3,x4,见图6,所测信号均为曲轴转角-幅值信号。
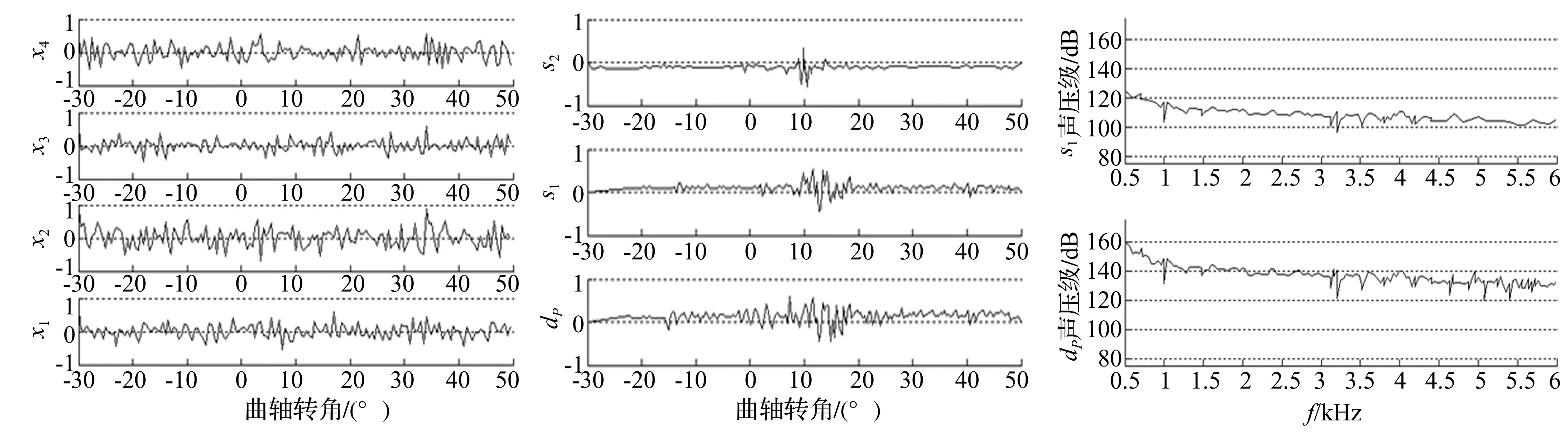
图6 柴油机混合振动信号
由于在上止点(TDC)附近,柴油机表面振动主要由缸内燃烧压力与活塞拍击压力共同产生的,该曲轴转角附近范围内辐射噪声主要为燃烧噪声及活塞拍击噪声。对活塞撞击缸体信号及缸内燃烧压力信号进行统计特性分析发现,活塞撞击缸体信号峰度值大于0,属超高斯信号,而缸内燃烧压力信号峰度值小于0,属亚高斯信号[14]。因此,利用MBLMS-TDS算法对上止点(TDC)附近测量所得振动信号x1,x2,x3,x4进行盲源分离,可得燃烧压力信号、活塞拍击信号。
用MBLMS-TDS算法,信号s1,s2将通过盲解卷积由测量信号x1,x2,x3,x4中分离出来,见图7。由图7看出,分离出的信号s1,s2均在上止点(TDC)附近产生,信号s2主要集中在10°曲轴转角附近。由于活塞与缸套存在间隙,在燃烧开始时活塞对缸套产生强烈敲击,信号s2紧随信号s1开始发生,且落后s1几度,由活塞撞击噪声时域特性[15]知,被分离出的s2为活塞撞击缸体激励。由于MBLMS-TDS算法为优化算法,因此s2会含其它能量较小成分。而s1虽在10°曲轴转角附近产生,但相对s2,s1持时长。此因柴油机燃烧存在滞燃期,且滞燃期后预混燃烧速度较快,导致缸内压力急剧升高。后续扩散燃烧使缸压明显下降。与已测得的维纳滤波缸压信号dP相比看出,在10°曲轴转角附近的曲线变化规律具有一定相似性,以2×10-5Pa为基准压力分别计算信号s1与维纳滤波缸压信号dP的压力级幅频曲线,比较二者在中频范围内压力级幅频曲线,见图8。对比可知,信号s1压力级幅频曲线与缸压信号dP压力级幅频曲线变化趋势相同,且信号能量主要集中在中频区,此因柴油机零件的固有频率多处于此频段,振动衰减较小,已被确认为燃烧冲击激励所致发动机缸体震荡。因此,用维纳高通滤波器测量的燃烧激励信号dP更精确,且方法简单。但测试中所用压力传感器昂贵且测试性能稳定性差。
6 展 望
本文后续工作将从两方面进行研究:①对置于柴油机缸体表面加速度传感器位置进行优化。传感器位置不同测量结果会不同。理论认为,传感器与分离盲源测量位置距离不易很近,若距离较近,系统混合响应矩阵为非广义逆矩阵[16],分离不出盲源。②柴油机缸内压力恢复及发动机载荷与发动机缸内压力变化关系。由于盲源分离不能恢复发动机激励源幅值。
7 结 论
(1) 介绍MBLMS算法,指出该算法的局限性,即仅能恢复出1个超高斯盲源,或1个亚高斯盲源。
(2) 将MBLMS算法与缩减盲源算法相合,对包含超高斯、亚高斯混合源信号进行盲解卷积,并证明该结合算法合理。
(3) 通过对四缸柴油机表面混合信号盲源分离,获得柴油机活塞撞击缸体激励及柴油机燃烧激励。结果与压力传感器所测燃烧激励信号相比表明,盲解卷积分离结果具有可靠性。本方法可用于轿车、航天器等噪声源识别,为消除噪声的可靠方法。
参 考 文 献
[1]焦卫东.基于独立分量分析的旋转机械故障诊断方法研究[D].杭州:浙江大学,2003.
[2]Ypma A, Leshem A, Duin R P W. Blind separation of rotating machine sources bilinears and convolutive mixture[R].Neurocomputing-special Issue on ICA/BSS,2002.
[3]Haykin S.Unsupervised adaptive filtering volume i:blind source separation[M]. New York: Wiley, Chichester,2000.
[4]Cichocki A, Amari S.Adaptive blind singal and image processing[M]. New York: Wiley,2003.
[5]叶红仙,杨世锡,杨将新.振动源信号的快速二阶统计算法研究[J].振动与冲击,2008,27(7):79-82.
YE Hong-xian,YANG Shi-xi,YANG Jiang-xin.Rapid second-order blind source separation algorithm for vibration signals[J]. Journal of Vibration and Shock, 2008,27(7):79-82.
[7]JG/T10-2009,钢网架螺栓球节点[S].
[8]范 重,杨 苏,栾海强.空间结构节点设计研究进展与实践[J].建筑结构学报,2011,32(12):1-15.
FAN Zhong,YANG Su,LUAN Hai-qiang. Research progress and practice of design of spatial structure joints[J]. Journal of Building Structures, 2011,32(12): 1-15.
[9]张毅刚, 周宜哲. 螺栓球节点刚度分析及其计算模型简化[A]. 第十二届全国现代结构工程学术研讨会论文集[C]. 北京:工业建筑杂志社, 2012:347-351.
[10]Jiang S F, Zhang C M, Yao J. Eigen-level data fusion model by integrating rough set and probabilistic neural network for structural damage detection[J]. Advances in Structural Engineering, 2011,14 (2):333-350.
[11]吴金志. 基于动力检测的网格结构损伤识别研究[D]. 北京:北京工业大学,2005:23-96.
[12]孙木楠. 基于神经网络的结构模型修改[J]. 振动与冲击, 2006, 25(1): 54-57.
SUN Mu-nan. Structural model updating based on neural network[J]. Journal of Vibration and Shock,2006, 25(1): 54-57.
[13]李金宝, 王 达, 刘 扬. 基于参数分析的子结构有限元模型修正技术[J]. 中外公路, 2012, 32(3): 227-232.
LI Jin-bao,WANG Da,LIU Yang.Sub-structure finite element model updating technology based on the parametric analysis[J]. Journal of China & Foreign Highway, 2012,32(3):227-232.
[14]韩 芳, 钟冬望, 汪 君. 基于径向基神经网络的有限元模型修正研究[J]. 武汉科技大学学报, 2011, 34(2):115-118.
HAN Fang, ZHONG Dong-wang, WANG Jun. Model updating based on radial basis function neural network[J]. Journal of Wuhan University of Science and Technology,2011, 34(2): 115-118.
