水电站机组与厂房结构耦合动力系统振动传递路径识别

孙万泉， 黄雄辉

(华北电力大学 可再生能源学院 水利水电工程系，北京 102206)

近年利用动力监测成果对水电站厂房及机组进行系统识别与反分析、探讨合理分析模型及动力特性已成研究热点。文献[1]以结构自振频率为目标函数，利用遗传算法对水电站厂房动态材料参数及边界条件进行识别；文献[2]在频域内对该厂房高频水力脉动荷载与结构阻尼参数进行优化识别；文献[3-4]对小波分析及遗传算法等在水电站结构分析与识别中应用进行阐述；文献[5]论述系统相干函数模型在水电站振动传递路径识别中应用。但该识别方法仅基于不同测点的振动相关程度分析，无法判别信号传递方向、具体振源传递路径。

事实上，水电站振动为由机组与厂房结构相互作用的耦合动力系统，其振动表现为多种信号的相互耦合及叠加，各处观测信号常表现为类似白噪声的随机信号[6]。因此，如何在复杂信息中识别出各振源信号的传递规律对研究水电站振动内在机理意义极其重要。为此，本文提出基于延时传递熵的水电站信息传递路径时域识别方法，通过数值模拟分析验证该方法的有效性，并结合原型观测研究水电站耦合动力系统振源信息传递规律。

1 延时传递熵

信息传递路径的识别需对多个信号各自特征及信号间信息关联与传递特性进行分析。传统的相关函数基于线性随机过程统计量，有对称特性，而非线性过程则不然。传统非线性统计量均源于两点自相关或信号功率谱，不含任何时间方向性信息。而传递熵为互信息函数，表示公共信息量的平均值，具有良好性质，定义时无假设变量间存在任何关系，因而其不仅能反映变量间线性关系，亦能描述变量间非线性关系。较传统相关函数传递熵含更多信息，可描述信号间线性、非线性关系，更适用于复杂系统信号分析。

传递熵用于研究不同信息流间的传递能量[7]。文献[8-9]提出延时传递熵理论，并将其应用于弹簧质量单元动力系统中信息流及损伤识别，获得较好效果。文献[10]对延时传递熵进行改进，研究二维延时传递熵在结构动力系统中应用。文献[11]通过理论、实验研究噪声对传递熵影响，结果表明传递熵在噪声环境中仍能较好识别单元间信息传递特性及非线性损伤特性。

1.1 延时传递熵定义

传统的马尔科夫过程表示随机序列x在某时刻发生只受该序列过去有限时间内影响，定义k阶马尔科夫序列为：

p[x(n+1)|x(n)(k)]=p[x(n+1)|x(n),x(n-1),…,x(n-k+1)]=p[x(1)|x(k)]

(1)

为方便表示可将式(1)中n略去。若x序列同时受另一随机序列y影响，则x在当前时刻发生的概率为：

(2)

基于两序列信号相互关系，传递熵定义为[6]：

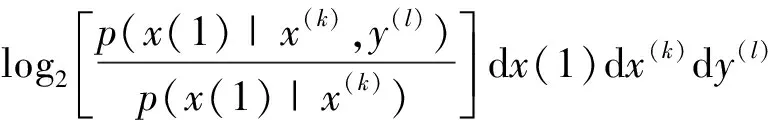
(3)

因此，传递熵提供了一种方法用于定量分析观测序列y对另一序列x未来发生值的影响，但式(3)的计算需求解高维概率密度。为简化计算令阶数k=l=1，并将时延参数τ引入序列y(n)中，传递熵可改写为延时传递熵形式[8-9]：

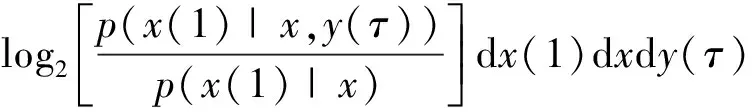
(4)

1.2 延时传递熵估计

据文献[12]，对离散观测序列x(n)，其熵可近似表示为核密度估计形式：

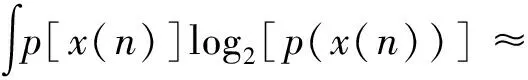
(5)

(6)

式中：N为采样点数；K(·)为核函数；ε为带宽参数。

用最常见的阶梯式核函数：

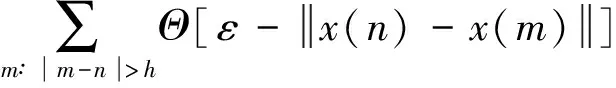
其中：Θ(·)为Heaviside函数[9]；h为Theiler窗口，用其可剔除暂时相关点。

将式(5)代入式(4)，延时传递熵可写为完全展开式[8]：

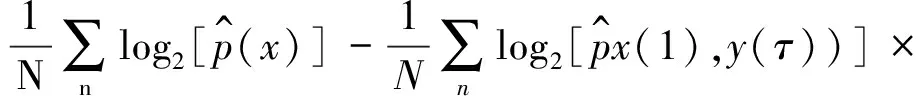
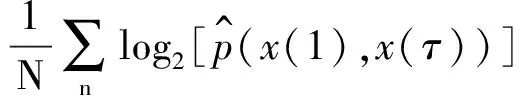
(7)

2 数值仿真分析

通过ANSYS有限元数值分析研究大型抽水蓄能电站振动系统中振源信息传递路径的延时传递熵识别方法。

2.1 计算模型与计算工况

该抽水蓄能水电站厂房结构混凝土材料为C25，钢筋为Ⅱ级钢。电站内布置4台单机容量300 MW竖轴混流可逆式水泵水轮机组，总装机容量1 200 MW，电站额定水头624 m。水轮机额定转速500 r/min，频率8.33 Hz。该水电站机组及厂房结构整体有限元模型与测点布置见图1、表1。厂房底部边界完全固结，四周为自由边界。

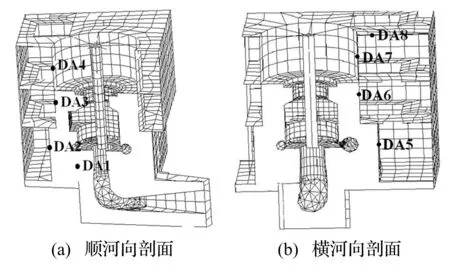
图1 振动观测点布置与有限元模型图

表1 振动观测点位置

数值模拟中各计算工况(施加荷载、采样频率250 Hz(0.004 s))为工况1：仅在下机架处施加水平向随机振动荷载，最大值653 N；工况2：仅在尾水管内施加随机面荷载，最大值65.2 N/m2；工况3：将上两种工况荷载同时作用在结构上。

2.2 延时传递熵计算结果及识别方法

据有限元计算响应，提取低点DA(i)、高点DA(i+1)测点某方向时程响应结果，分别作为随机序列x、y，代入式(7)分别计算延时、超时，再经排列便可得出T(i+1→i)结果(即高点DA(i+1)对低点DA(i)的延时传递熵)；反之，将DA(i)、DA(i+1)分别作为序列y、x进行计算，便可得出T(i→i+1)结果。相邻两测点T(i+1→i)、T(i→i+1)结果曲线见图2～图4。

图2为工况1径向动位移响应的延时传递熵计算结果。由图2看出，在中间轴及左侧(延时τ≤0部分)，可据熵值大小判断信息传递方向，即信息传递正方向(即真实信息传递方向)熵值大于负方向熵值。因该工况中荷载作用在下机架处，距离DA3最近，据信息传递路径最短原则，振动传递路径应为DA1← DA2← DA3→ DA4；DA5←DA6→DA7→DA8。当τ≤0时，T(3→2)>T(2→3)，T(2→1)>T(1→2)，T(7→8)>T(8→7)等。该现象主要因DA3信息超前于DA2，故当τ≤0时DA3→DA2的传递能量大于相反方向。因此，实际运用中可通过此传递熵特性综合分析，识别出振动信息传递方向。延时τ≤0部分的传递熵大小说明哪个方向信息更超前，而该现象在τ>0中表现为传递熵峰值点出现的早晚。即在τ>0部分若传递熵曲线峰值点更早出现(即更靠近中间轴)，则该传递方向信息更超前。但在实际问题中因信息传递的复杂性、正反信号交叉重叠等，以上现象有时较难区别。因此，应据熵值大小、峰值点位置、熵曲线偏移方向等多种方法综合分析识别。

图2 工况1各测点间相对延时传递熵

用同样方法计算得工况2、3中径向动位移响应的延时传递熵，典型结果见图3、图4(篇幅所限，不列全部结果)。由工况2中传递熵曲线看出，当τ≤0时，T(低层→高层)>T(高层→低层)(例：T(2→3)>T(3→2))，由该结果可判断出振动信息全部由最底层向上传递。该识别结果与真实荷载激励位置、信息传递方向一致。由图4看出，工况3中因尾水管处荷载激励使τ≤0时，T(1→2)>T(2→1)，信息传递方向为DA1→DA2。但因同时存在下机架处荷载作用，在DA2与DA3间却表现出向下的信息传递。因此，由以上结果可识别出结构同时承受两处荷载激励，识别出荷载作用位置。

通过对其它不同结构、荷载作用方式进行模拟分析，结论与前述一致，也可证明该识别方法的有效性。

2.3 噪声对识别方法影响

将振动观测结果加入5%、10%不同水平白噪声后分别进行延时传递熵计算。结果表明，噪声的存在减小了τ≤0区间相对传递熵大小，但仍能判别出正方向(即真实信息传递方向)传递熵大于负方向，以工况1的DA2、DA3为例，见图5。由图5看出，虽有噪声干扰，该识别方法对分析信息的传递方向仍然有效。

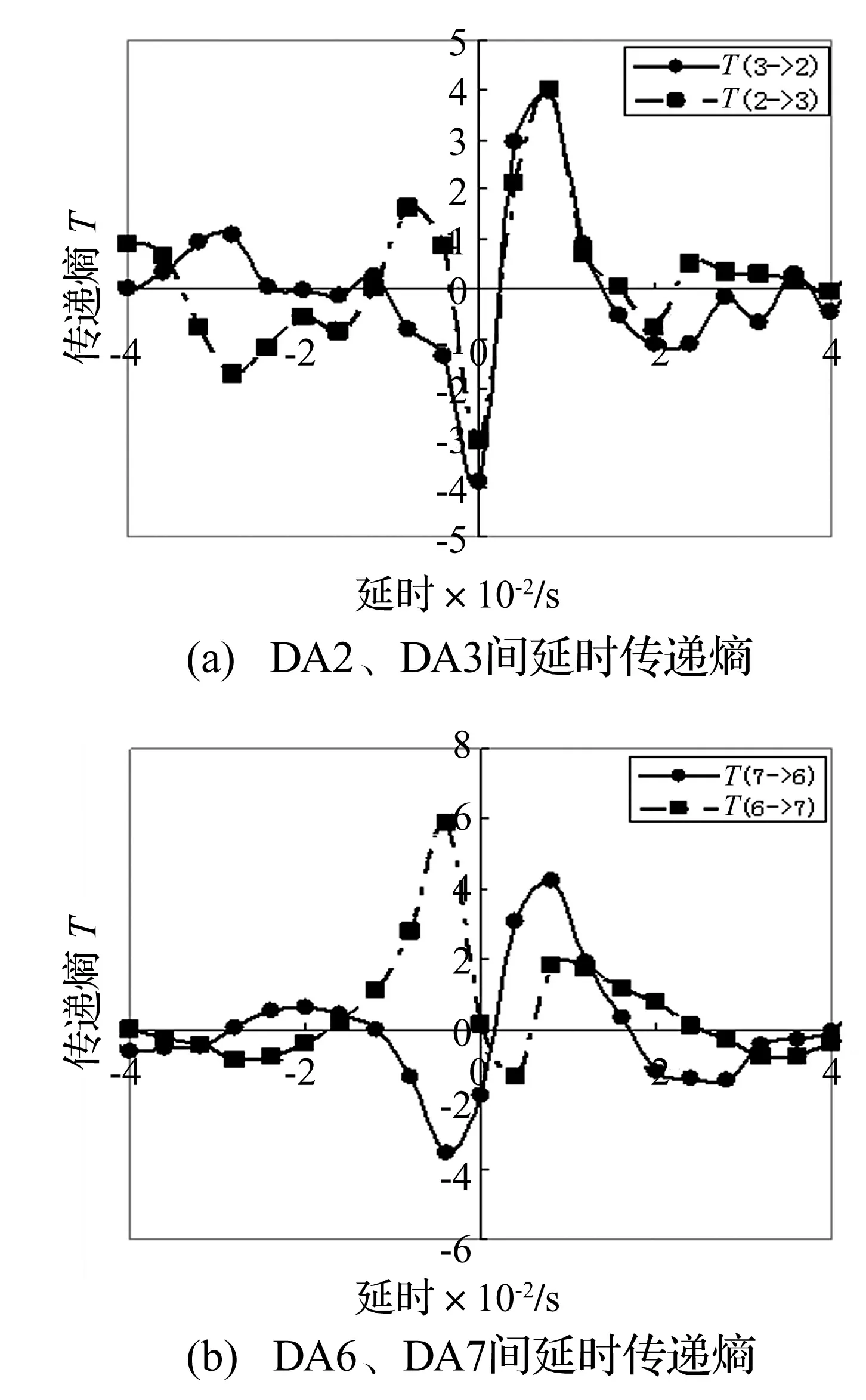
图3 工况2中部分测点间相对延时传递熵

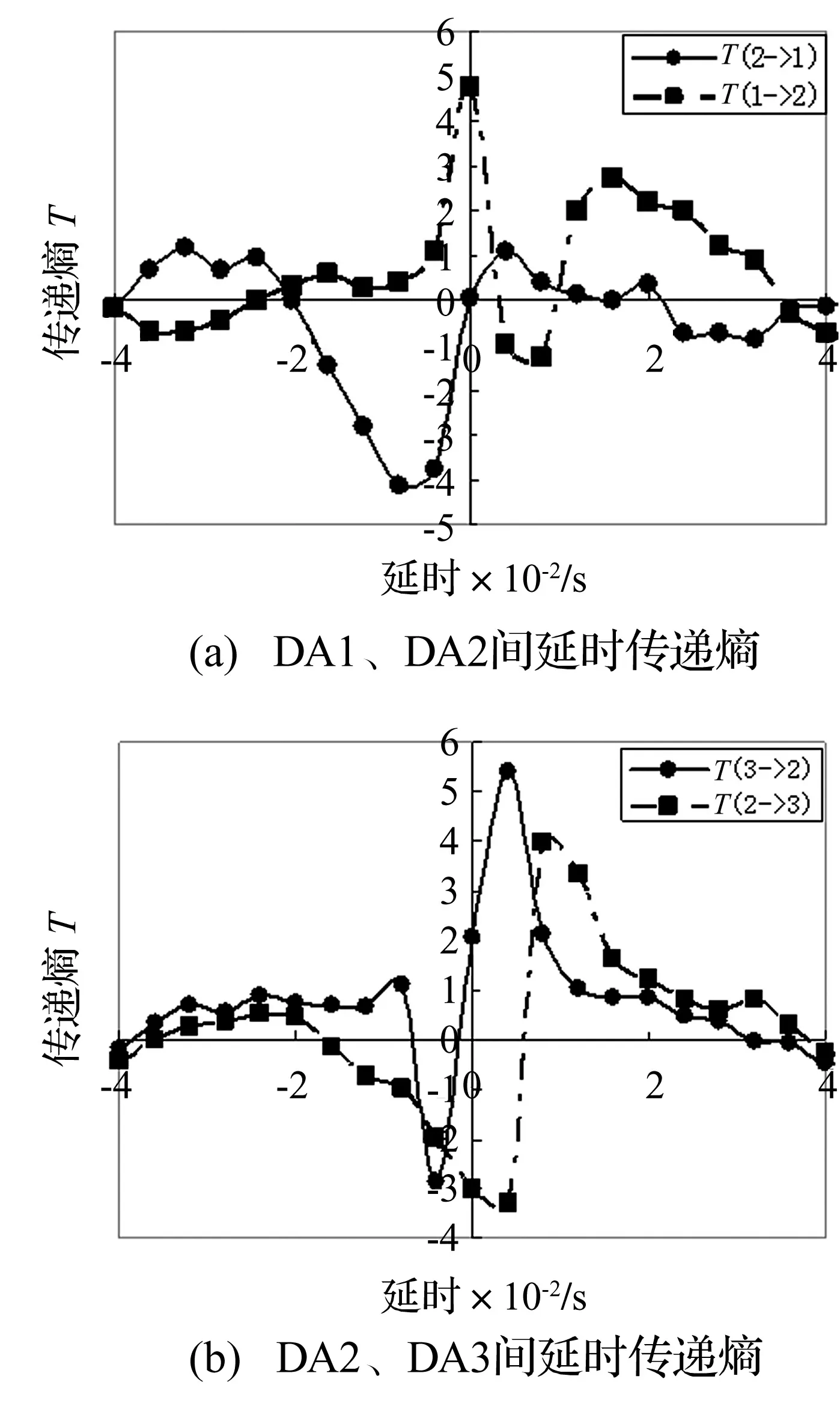
图4 工况3中部分测点间相对延时传递熵

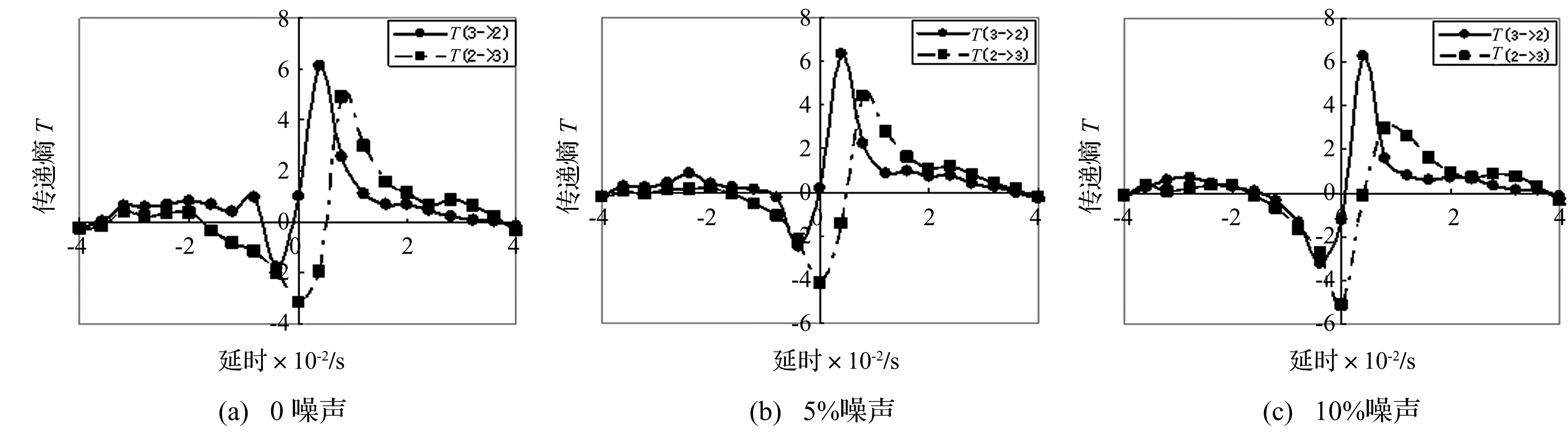
图5 工况1 DA2、DA3不同水平噪声对延时传递熵影响

3 现场测试信号识别

该抽水蓄能电站振动现场监测采用EDS24-24工程数字振动仪，采样率250 Hz。现场测点为施工时事前埋入，布置情况与数值分析同图1。测试工况为满负荷发电，提取各测点水平径向加速度振动信号进行分析。水电站直接测量所得信号为多种振源相互耦合、叠加的随机振动信号，包括机械振动、水力振动、电磁振动信号等。先对直接所测原始信号识别分析，再用小波分析提取其中两主要成份信号(转频振动、转轮叶片数频率振动信号)进行识别分析。

3.1 原始测量信号识别

图6为各测点间相对方向延时传递熵。由计算结果知，在τ≤0区间，除DA2、DA3外，其它各测点间传递熵值无明显大小区分。而通过DA2、DA3间传递熵可识别出该两测点间的信息传递方向为DA2→DA3。说明水电站整体振动由多种传递信号相互耦合结果，表现为无方向性。但在厂房上游侧蜗壳附近表现出较明显的信息向上传递特性(即DA2→DA3)，分析原因应为蜗壳进水口与流道内产生的不均匀水流造成顺河向水力脉动，又通过蜗壳流道壁及相关机械附件传递，为该运行工况最突出振源。

图6 原始测量信号相对方向延时传递熵

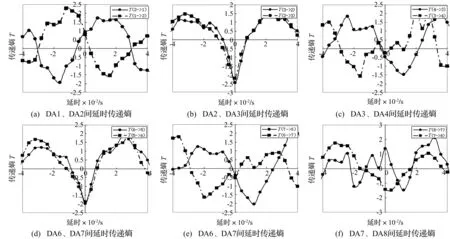
图7 8.33 Hz转频振动信号相对方向延时传递熵

3.2 8.33 Hz转速频率振动信号识别

利用小波分析工具从直接测量的综合信息中提取8.33 Hz转速频率时频信号进行延时传递熵计算，结果见图7。由图7看出，该传递熵结果表现出较强的方向性。除DA1、DA2间信息传递方向向上外，其它各测点间传递熵均表现出方向向下的传递特性；在转轮以下8.33 Hz信号主要为尾水管内的水力脉动激励；而蜗壳层以上部位8.33 Hz信号主要由转子不平横振动造成，该振动通过上、下机架向下传递，且主要通过上机架向下传递。

3.3 转轮叶片数频率58 Hz振动识别

转轮叶片数频率58 Hz振动为水电站主要振源之一。通过小波分析提取该时频信号进行延时传递熵计算，结果见图8。由图8看出，厂房上游侧振动传递路径为DA1→ DA2← →DA3←DA4；厂房左侧振动传递路径为DA5←DA6→DA7→DA8。说明因转轮叶片数频率振动引起的水力脉动不但直接作用于尾水管直锥段壁(或转轮室)向上传递，且通过机组大轴传递到上、下机架后再作用于厂房结构。厂房上游侧主要通过上机架传递，厂房左侧主要通过下机架传递。

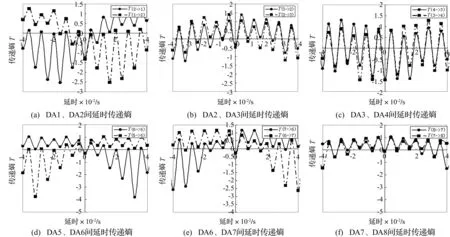
图8 转轮叶片数频率58 Hz振动信号相对方向延时传递熵

4 结 论

(1) 本文提出基于延时传递熵理论的水电站振动信息传递路径及传递方向时域识别方法，并通过有限元数值模拟分析验证该方法的有效性及抗噪声能力。

(2) 结合原型观测的振动资料，研究水电站耦合动力系统振源信息传递规律。对直接所测原始信号识别分析，用小波分析提取其中转频振动、转轮叶片数频率振动两主要成份信号进行识别分析，研究不同振源信息传递方向及传递路径。

本文研究为进一步分析水电站振动传递规律、振源位置及内在机理提供新时域识别方法及相关研究结论。

参 考 文 献

[1]马震岳，孙万泉，陈维江. 基于遗传算法的地下发电厂房动态识别[J]. 大连理工大学学报，2004，44(2)：292-296.

MA Zhen-yue, SUN Wan-quan,CHEN Wei-jiang. Dynamic identification for underground power house based on genetic algorithm[J]. Journal of Dalian University of Technology,2004,44(2):292-296.

[2]SUN Wan-quan, MA Zhen-yue, YAN Xu-dong,et al. Intelligent identification of underground powerhouse of pumped-storage power plant[J]. Acta Mechanica Sinica, 2005,21(2):187-191.

[3]练继建, 王海军, 秦 亮. 水电站厂房结构研究[M].北京：中国水利水电出版社,2007.

[4]李松辉, 练继建. 水电站厂房结构模态参数的遗传识别方法[J]. 天津大学学报, 2009,42(1):11-16.

LI Song-hui, LIAN Ji-jian. Genetic algorithm for hydraulic power house modal parameters identification[J]. Journal of Tianjin University, 2009,42(1):11-16.

[5]毛汉领, 熊焕庭, 沈炜良. 偏相干分析在水电站振动传递路径识别的应用[J]. 广西大学学报,1998(1):6-9.

MAO Han-ling, XIONG Huan-ting, SHEN Wei-liang. The partial coherence annalysis and it′s application on the identification of vibration transfer path on the hydraulic power station[J]. Journal of Guangxi University,1998(1):6-9.

[6]幸享林,陈建康,廖成刚,等. 大型地下厂房结构振动反应分析[J]. 振动与冲击, 2013, 32(9): 21-27.

XING Xiang-lin,CHEN Jian-kang,LIAO Cheng-gang,et al.Viration response of large underground powerhouse [J].Journal of Vibration and Shock,2013,32(9):21-27.

[7]Schreiber T.Measuring information transfer[J].Physical Review Letters,2000,85(2):461-464.

[8]Nichols J M. Examining structural dynamics using information flow[J].Probabilistic Engineering Mechanics,2006,21 (4):420-433.

[9]Nichols J M, Seaver M, Trickey S T. A method for detecting damage-induced nonlinearities in structures using information theory[J]. Journal of Sound and Vibration,2006,297(1-2):1-16.

[10]Overbey L A, Todd M D.Dynamic system change detection using a modification of the transfer entropy[J]. Journal of Sound and Vibration,2009,322(1-2):438-453.

[11]Overbey L A, Todd M D.Effects of noise on transfer entropy estimation for damage detection[J]. Mechanical Systems and Signal Processing,2009,23(7):2178-2191.

[12]Liebert W, Schuster H G. Proper choice of the time delay for the analysis of chaotic time series[J].Physics Letters A,1989,142(2-3):107-111.