几类带宽极图
2014-09-04陆锋
陆 锋
(湄洲湾职业技术学院 福建莆田 351254)
几类带宽极图
陆 锋
(湄洲湾职业技术学院 福建莆田 351254)
本文主要在e(p,p-2)的所有极图的研究的基础上,进一步考虑带宽为p-3的图的补图结构,从而确定了e(p,p-3)(p≤9)以及e(p,p-4)(p≤8)的所有极图,对已有的结论进一步做了推广.
图,带宽,极图
图论是数学的一个分支,特别是组合数学的重要分支之一.其广阔的应用领域涵盖了人类学、计算机科学、化学、环境保护、流体动力学、电信领域等等.在实际生活、生产和科学研究中,有许多问题可以利用图论的方法来解决.在图论的研究课题中,有一类相当有趣的问题,那就是图的带宽问题.由于它在数值计算、编码理论、网络设计及结构力学分析、超大规模集成电路(VLSL)布线设计等方面的实际应用,引起了国内外学者的关注.图的带宽问题是一个既有广泛的实际应用背景,又是极有趣味的数学课题.笔者首先介绍一些与带宽极图相关的理论成果.定义带宽极图如下:
记e(p,B)=min{‖G‖∶|G|=p,B(G)=B,G,其中},|G|,‖G‖分别表示图的顶点数和边数.达到此最小值的图就称为e(p,B)的一个极图.
1 准备知识
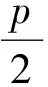
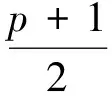
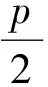
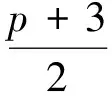
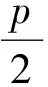
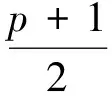
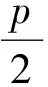
定理1.8[6]设 ,则:
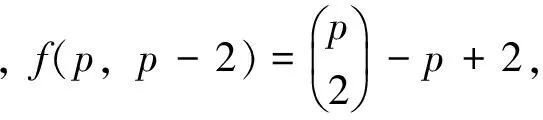


2 e(p,p-3)(p≤9)的所有极图
文献[6]考虑了e(p,p-2)的极图基础上,本文笔者主要考虑为e(p,p-3)的极图问题,结合已有结论确定e(p,p-3)的所有极图,对文献[7]的结论进一步作了推广.
定理1.1易得,当p≤6时e(p,p-3)的所有极图.当p=4时,e(4,1)=3,p4是e(4,1)的唯一极图.当p=5时,e(5,2)=4,图1所示为e(5,2)仅有的两个极图.当p=6时,e(6,3)=5,k1,5是e(6,3)的唯一极图.

图1
文章[7]通过考虑e(7,4)极图的补图结构性质,确定了e(7,4)的所有极图是下列三种图形的补图(即图2中(1)(2)(3)的补图)
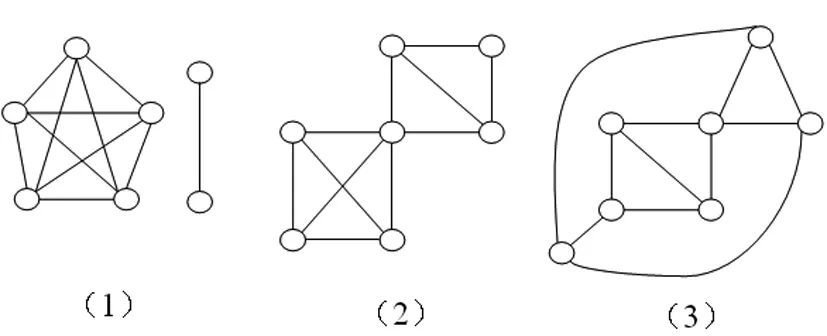
图2
现在笔者考虑当p=8时,即e(8,5)的极图及其构造的形式.首先笔者考虑e(8,5)的极图的补图,为此先给出如下命题:
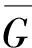
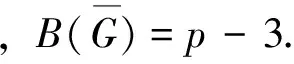
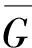
对不含H3的图,可以分两种情况讨论(1)图中不含C4;(2)图中含C4.
下面对以上两种情况进行讨论:
(1)如果图G不含有C4的图的性质,则在文献[8]给出不含C4且边数最多的连通图情形如下定理:
引理[8]设G顶点数为p、不含C4、边数最多的连通图,则边数‖G‖(1≤p≤21)如表1所示:

表1
(2)现在考虑如果图G含有C4但不含有H3的情况.本文仅考虑顶点数不大于8的连通图,由于点数较小,可以确定顶点数8的边数最多的连通图G的,其中:C4⊂G、H3⊄G、Δ(G)≤6.按照图G含有 但不含 的性质对 有如下的导出子图(如图3)的可能性进行讨论(同时含有不止一种情况下,本文就考虑边数尽可能多的导出子图)
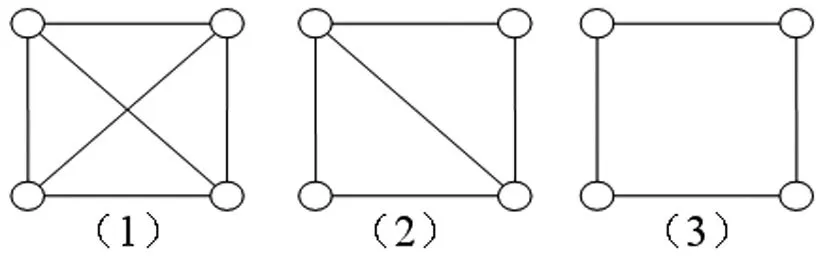
图3 F含有C4但不含H3的性质导出子图
当p=8时,且满足下列条件C4⊂G、H3⊄G、Δ(G)≤6.则G仅有如图4所示的4种形式.
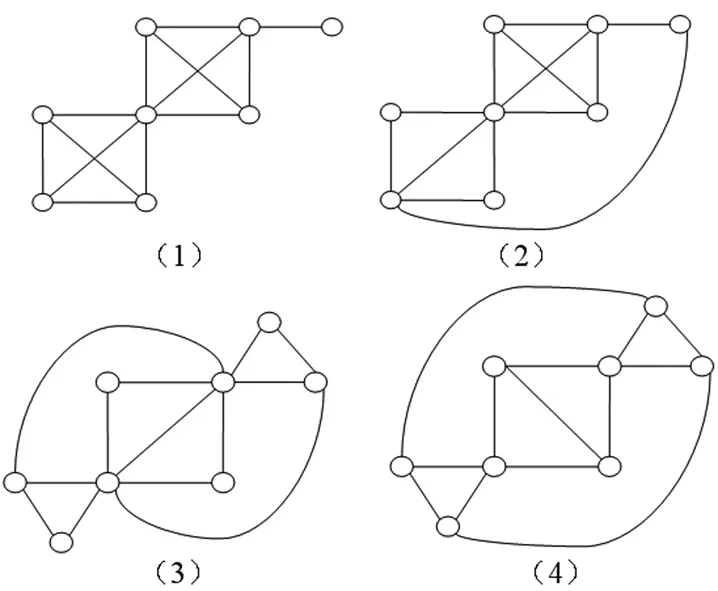
图4 p=8时, 符合条件图
由以上可得如下性质:当顶点数p=8时,边数最多的连通图G,其中C4⊂G、H3⊄G、Δ(G)≤6,则‖G‖=13.和比较表1,可见当p=8时,对于相同顶点数p的图G,含有子图C4的图边数更多,因此,就只需考虑含C4的情况.
下面本文考虑e(8,5)的所有极图:首先,寻找满足下述条件的顶点数为8的边数最多的图G,G满足d(v)≤6,∀v∈V(G),含有p4⊂G,H3⊄G.令Gm为图G中顶点数最多的连通分支.综上满足条件P4⊂G、H3⊄G、Δ(G)≤6的图 的边数为13.仅有如下图5的三种形式.由命题2.1知e(8,5)的所有极图只有5种分别为如图5所示的图形.
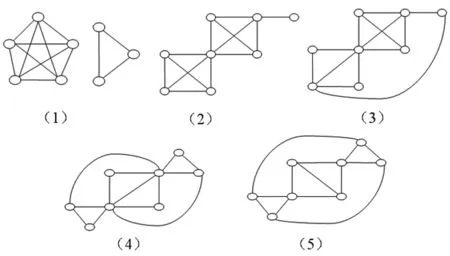
图5 e(8,5)的所有极图
同理,考虑当p=9时,且满足下列条件:P4⊂G、H3⊄G、Δ(G)≤7.则 仅有如图6所示的2种形式.

图6 p=9时,G符合条件图
由以上可得如下性质:当顶点数p=9时,边数最多的连通图G,其中:P4⊂G、H3⊄G、Δ(G)≤7,则‖G‖=16.和比较表1,可见当p=9时,对于相同顶点数p的图G,含有子图C4的图边数更多,因此,只需考虑含C4的情况.由此可以得到e(9,6)的所有极图,其中G满足d(v)≤7,∀v∈V(G),含有P4⊂G、H3⊄G、Δ(G)≤7. 的图G的边数为16,仅有如图7的3种形式.
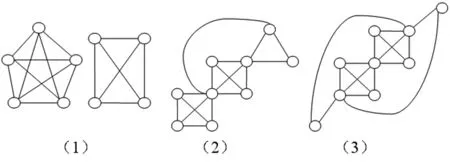
图7 e(9,6)的所有极图
3 e(p,p-4)(p≤8)的所有极图
综合所述,实际上可以得到e(p,p-4)(p≤8)的所有极图.当p=5时,e(5,1)=4,P5是e(5,1)的唯一极图.当p=6时,e(6,2)=5,图8所示是e(6,2)仅有的4个极图.当p=7时,e(7,3)=6,图9是e(7,3)的所有极图.当p=8时,e(8,4)=7,k1,7是e(8,4)的唯一极图.
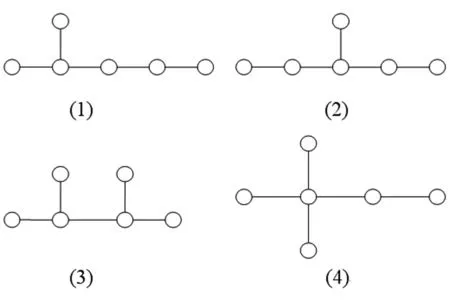
图8 e(6,3)的4个极图
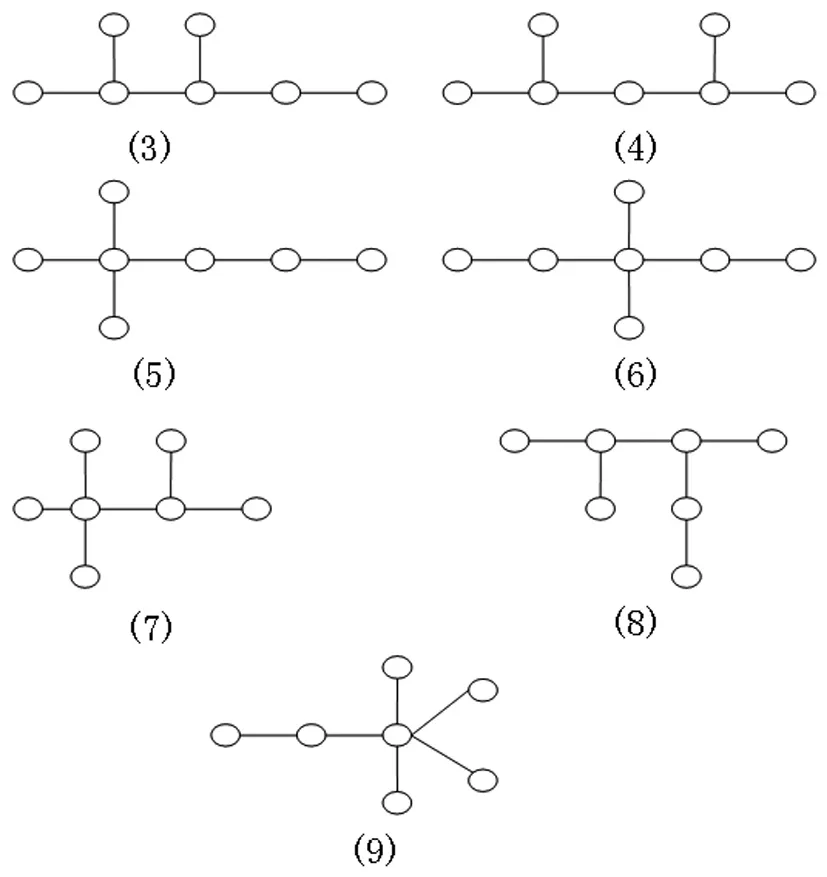
图9 e(7,3)的所有极图
对于e(p,p-4)(p>9)的极图由定理1.1至定理1.6可知,可以找到相应的极图,但是要把所有的极图一一找出是有一定的困难的,有待今后进一步研究.
[1]RD Dutton and RC Brigham. On the size of graphs of a given bandwidth [J]. Disc Math 1989,76:191.
[2]Y Alavi, J Liu, J McCanna,et al. On the minimum size of graphs with a given bandwidth [J]. Bu11 Inst Comb App1,1992,33(6):22.
[3]PCB Lam and Y Lin. An extremal graph problem on bandwidth [S]. Manuscript. 1996.
[4]郝建修.关于带宽极值问题的两个结果[J].应用数学,2000,13(3):73.
[5]林冶勋.图带宽问题的若干刻划[J].运筹学学报,2000,4(2):1.
[6]陆锋.带宽极图的一个反例[J].九江学院学报(自然科学版),2013,28(3):68.
[7]袁文彬.关于图的带宽问题[D].福州:福州大学.2009.
[8]Yang Aifeng, Lin Yixun. Some results on an extreml bandwidth graph problem. Mathematica Applicata,2003,16(1):143.
(责任编辑李平)
2014-4-23
陆锋,21848119@qq.com.
O 157.5
A
1674-9545(2014)02-0058-(04)
