基于三坐标测量机的涡轮钻具叶型测量与分析
2014-09-04孟晓平王作文李一岚
孟晓平, 袁 园, 龚 彦, 王 彪, 王作文, 李一岚
(1.西南石油大学机电工程学院,四川成都 610500;2.中国石油新疆油田分公司陆梁油田作业区,新疆克拉玛依 834000)
在油气田开发工程中,涡轮钻具作为一种重要的井下动力钻具已被广泛应用于油田现场,并产生了良好的经济效益[1]。不同的工作条件下,需要使用不同性能的涡轮钻具,而涡轮钻具的性能主要由其定转子决定。涡轮钻具的定转子由形状复杂的叶片组成,叶片的叶型不同,定转子的性能不同,所以优化涡轮钻具叶型设计是提高涡轮钻具性能的重要一环[2]。常用的涡轮钻具叶片叶型很多,效率差异很大,对这些叶片叶型进行测量,并结合现场使用情况进行对比分析,有助于设计出更高效的涡轮钻具叶片。但是,目前并没有专门针对涡轮钻具叶片这种小尺寸曲面构件的测量研究方法,而采用常规曲面测量研究方法测量出来的结果误差太大,达不到分析研究的精度要求,因此失去了涡轮钻具叶型测量的意义。为此,笔者提出一种基于三坐标测量机的涡轮钻具叶片叶型的测量方法,一方面可以检验其制造精度,另一方面可以研究叶片的动力特性。
1 叶片的测量方式及方法
1.1 叶片的测量方式
由于受到所钻井井眼径向尺寸的限制,涡轮钻具的定转子均采用整体式结构,通过精铸加工一次成型。为了保证涡轮钻具的水力效率,叶片采用带冠形式,如图1、图2所示。

图1 涡轮钻具的定子Fig.1 Stator of turbodrill

图2 涡轮钻具的转子Fig.2 Rotor of turbodrill
从图1、图2可以看出,涡轮钻具定转子叶栅的叶片被封闭在叶冠和轮毂之间。在机械加工领域,常采用基于三坐标测量机的接触式测量的精密测量方式,并以影像测量、激光扫描测量等作为辅助测量方式。其中,影像和激光扫描两种非接触测量方式,可在不破坏被测零件的条件下采用[3],但采用影像测量或激光扫描方式测量弯度较大的叶片时,沿叶片轴向弦长方向,叶片的进口段会遮住出口段的部分区域,叶片的最大弯度位置部位会遮住下一叶片的出口段某一区域,因此产生测量盲区。而接触式测量是通过测针接触所测零件表面获取触点准确位置来完成测量,为便于测针按运动轨迹完成测量,有时需要破坏零件,但其测量精度较高。由于涡轮钻具叶片叶型测量选用的通常是已经使用过的涡轮定转子或专门生产出来用作测量的涡轮定转子,不要求保证其完整性,并对测量精度要求较高,所以选择接触式测量方式用以测量涡轮钻具的定转子叶片叶型。
1.2 叶片的测量方法
采用接触式测量方式时,测针测头与零件被测部位接触,触发传感器获取相应触点的准确位置坐标。相对测针而言,涡轮钻具定转子叶片尺寸小,叶片密集,测针难以伸入两叶片之间的流道中获取叶型数据。因此,需将叶片去冠,使叶片截面暴露,方便测针深入。切去叶片叶冠需沿特定路径:一是沿垂直于半径方向的一条直线轨迹切割(如图3所示);二是沿某一半径的基元级轨迹切割(如图4所示)。因为,涡轮钻具的叶片为平面直叶片,叶型在不同半径处的基元级相同。钻井液在涡轮钻具中的流动,实际为在直径为D1(叶尖直径)和D2(叶根直径)的两个同轴圆柱面间的空间运动,根据流体机械的圆柱层无关理论,可将其看作无数圆柱层钻井液的合成运动[1]。不同半径处圆柱层上的质点,其所受的周向牵连速度大小不同,为研究方便,简化为平均水力半径为D/2的圆柱面上的流动进行计算[1],故取基元级切割路径的半径为平均水力半径D/2(见图4)。
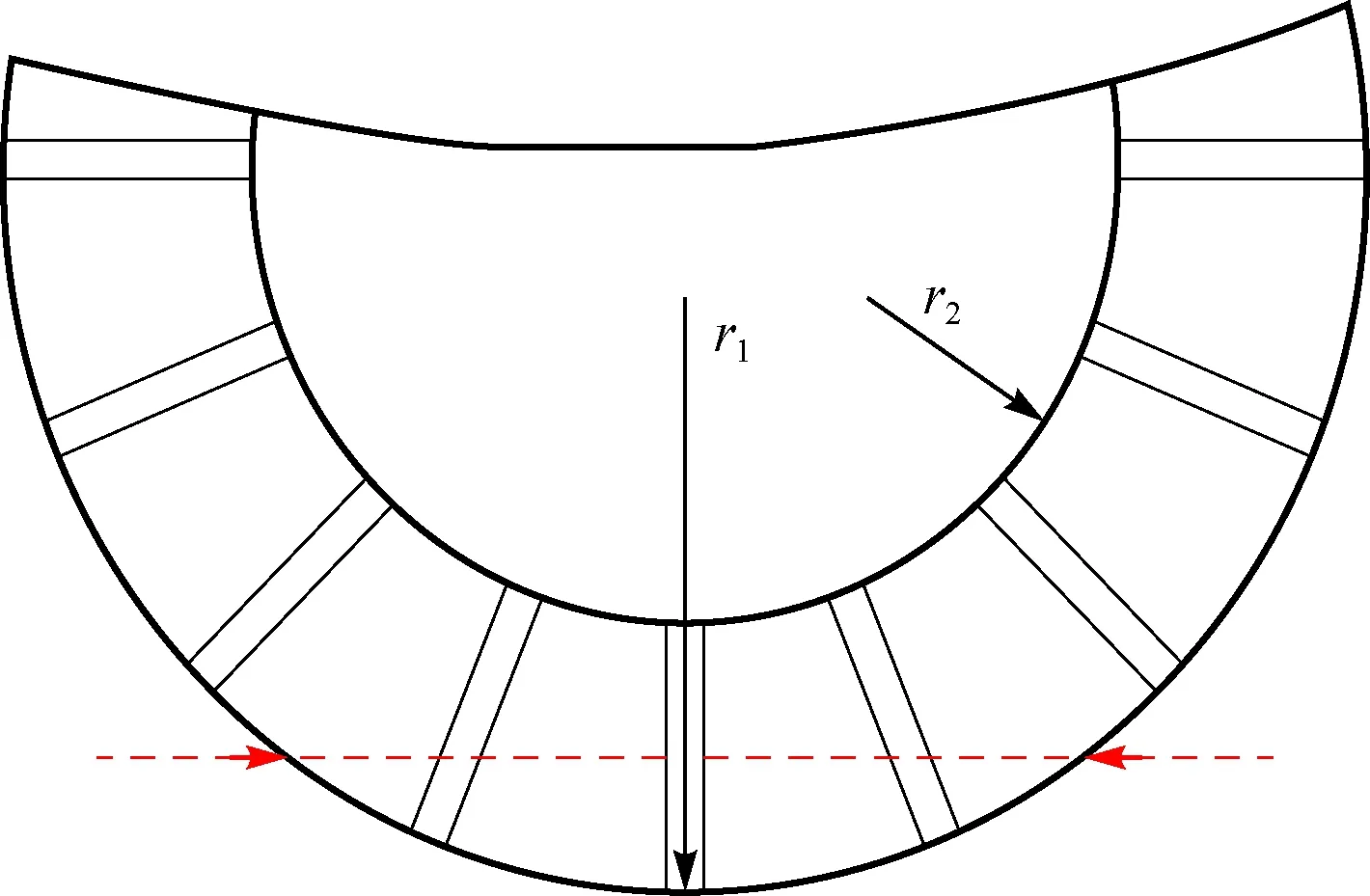
图3 直线切割路径Fig.3 Path of straight line cutting
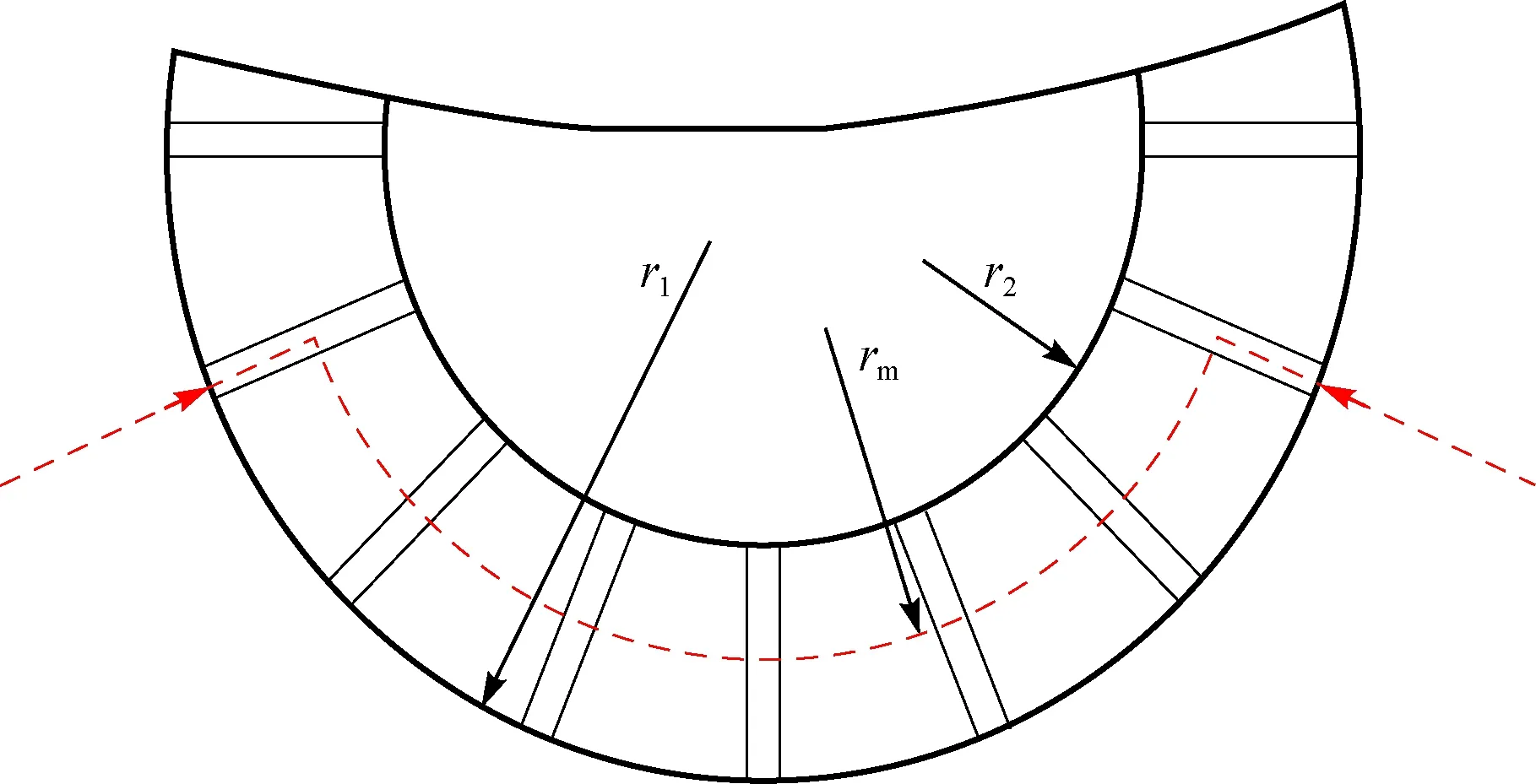
图4 基元级切割路径Fig.4 Path of elementary stage cutting
平均水力半径计算公式为:
(1)
式中:rm为平均水力半径,即D/2,mm;r1为叶尖半径,mm;r2为叶根半径,mm。
涡轮钻具的叶片为平面直叶片,沿涡轮径向摆放,所以与径向垂直平面上的叶型便是真实的叶片叶型。采用直线切割路径时,只有与切割路径垂直的叶片才能真实反映叶片的截面形状,其余被切到的叶片均被切废,该切割方法适用于叶片比较稀疏的叶栅。采用基元级切割路径切割叶片时,被切叶片均能真实反映叶片叶型。
涡轮钻具定转子叶型是按压力面曲线和吸力面曲线分别表达的,故测量时采用AC-DIMS软件中的自动曲线测量方式分别测其吸力面和压力面,该测量方式精度可达0.002 4 mm。为了保证能够测量到完整的压力面型线或吸力面型线,在测量压力面时,测量的起始点和结束点均要取在吸力面型线上;同理,在测量吸力面时,测量的起始点和结束点选取在压力面型线上。在处理数据时,计算压力面型线要去掉所测吸力面型线的点,计算吸力面型线则要去掉所测压力面型线上的点。测量结果如图5所示(图中,红色轮廓线是测针测头的运动轨迹,黄色曲线为测量数据点的集合)。
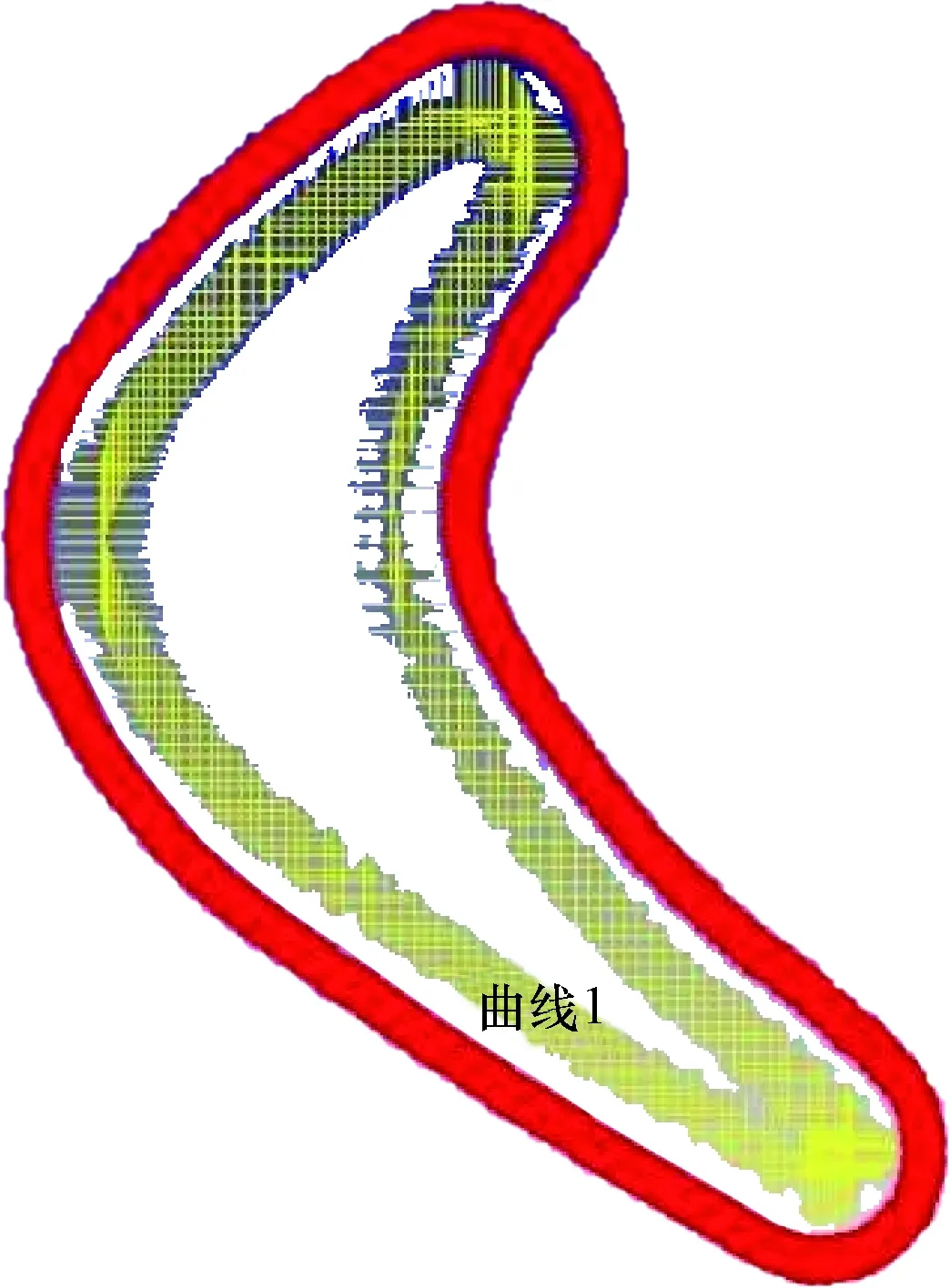
图5 叶型测量结果Fig.5 Measuring result of blade profile
2 基于点分组控制三次曲线的叶型计算
在传统的精密铸造加工过程中,通过一系列叶片型线上的点来确定蜡模,这些点在设计时给定。在接触式测量中,很难直接准确测取到这些点,而通过采取测点数据拟合的方式可以得到叶型曲线,由叶型曲线则可以准确获得加工时所选用点的坐标,再与设计时给定的点对比,就可以检验加工出的叶片的精度[4]。在现代加工制造的技术手段中,也可通过叶型曲线方程来加工叶片。在测量从国外引进的涡轮钻具的叶片叶型时,获得未知叶型的曲线方程后,就可建立起相应叶片的CAD模型,以便后续做叶片的流体动力分析,研究其性能[5]。
流体在涡轮钻具的定转子中流动时,叶片压力面型线和吸力面型线均为流场中的流线。根据型线为流线的条件可知,型线必须具有连续的三阶导数,才能满足光滑流动的要求[6]。该条件下的最简单情况是第三阶导数为常数,对应的多项式为三次多项式,其一般表达式为:
y=a0+a1x+a2x2+a3x3
(2)
三次多项式控制的曲线大致形状相似,只是因各项系数不同曲线的陡缓程度有区别,或者方向不同,在小范围内不发生震荡,切线斜率符号改变不多于一次,并且是光滑的[7]。在测量叶型数据点时,各点之间的步长为0.5 mm以下,即每两个点之间控制的叶片型线特别短,因此在如此小的范围内,三次曲线不会发生振荡,故采用该方法来拟合计算叶型是可行的[8-9]。
根据式(2),三次多项式的一般形式具有4个未知系数,因此采用4个已知点,建立4个线性方程组,即可求得该三次多项式的表达式:
(3)
拟合后的型线必须是光滑的,因此要求各段三次曲线应平滑连接,为了保证该条件,要求连接点上前后的切向向量要同向[10]。小范围内的三次曲线,其上任意一点前后的切向向量相同,根据该特点把型线上的所测点进行分组,每组点控制1条三次曲线,每组共有4个点,N个所测点可以分为N-3组。把这些测点记为s1,s2,…,si,…,sN,任一点si的坐标用(xi,yi)表示,则分组情况如下:
第1组:s1,s2,s3,s4控制曲线c1;
第2组:s2,s3,s4,s5控制曲线c2;
第3组:s3,s4,s5,s6控制曲线c3;
……
第N-3组:sN-3,sN-2,sN-1,sN控制曲线cN-3。
根据分组情况知,以上每两组相邻的点组合总有3个共有点。因此,拟合后的叶型曲线上每两条相连接的三次曲线有3个共同控制点,对曲线ci而言为后3个点,对曲线ci+1而言是前3个点,那么这两条曲线的3个共同点上各点的切向向量方向是相同的,差别在于大小不一致,这是因为三次曲线在小范围内是光滑的。从数学上讲,这两条三次曲线相交,构成一个三次方程,满足一定条件的三次方程,可以有3个实根,也就满足上述要求。
因此,采用上述方法来拟合的型线方程可以简写为:
(4)
前文已述,接触式测量是由测针测头依次触碰叶片表面而获得的数据点,所有数据点均为有效数据点,不存在冗余数据点,用于拟合曲线的数据点也是有效的。由此,可根据测量数据拟合得到叶型曲线,完成对叶栅叶型的测量与计算。
3 实例分析
对φ127.0 mm涡轮钻具某型转子的叶片叶型进行了测量,将工件坐标系建立在转子叶栅出口平面上,测量步长为0.2,获得的有效数据点196组,数据588个。按照前述方法进行叶型计算,得到各组控制点控制的三次曲线193条(图6所示为测量数据处理界面及前6条拟合曲线的方程)。为便于对比通过测量点拟合出的叶型与原设计叶型,将拟合叶型导入到AutoCAD中,结果如图7所示。
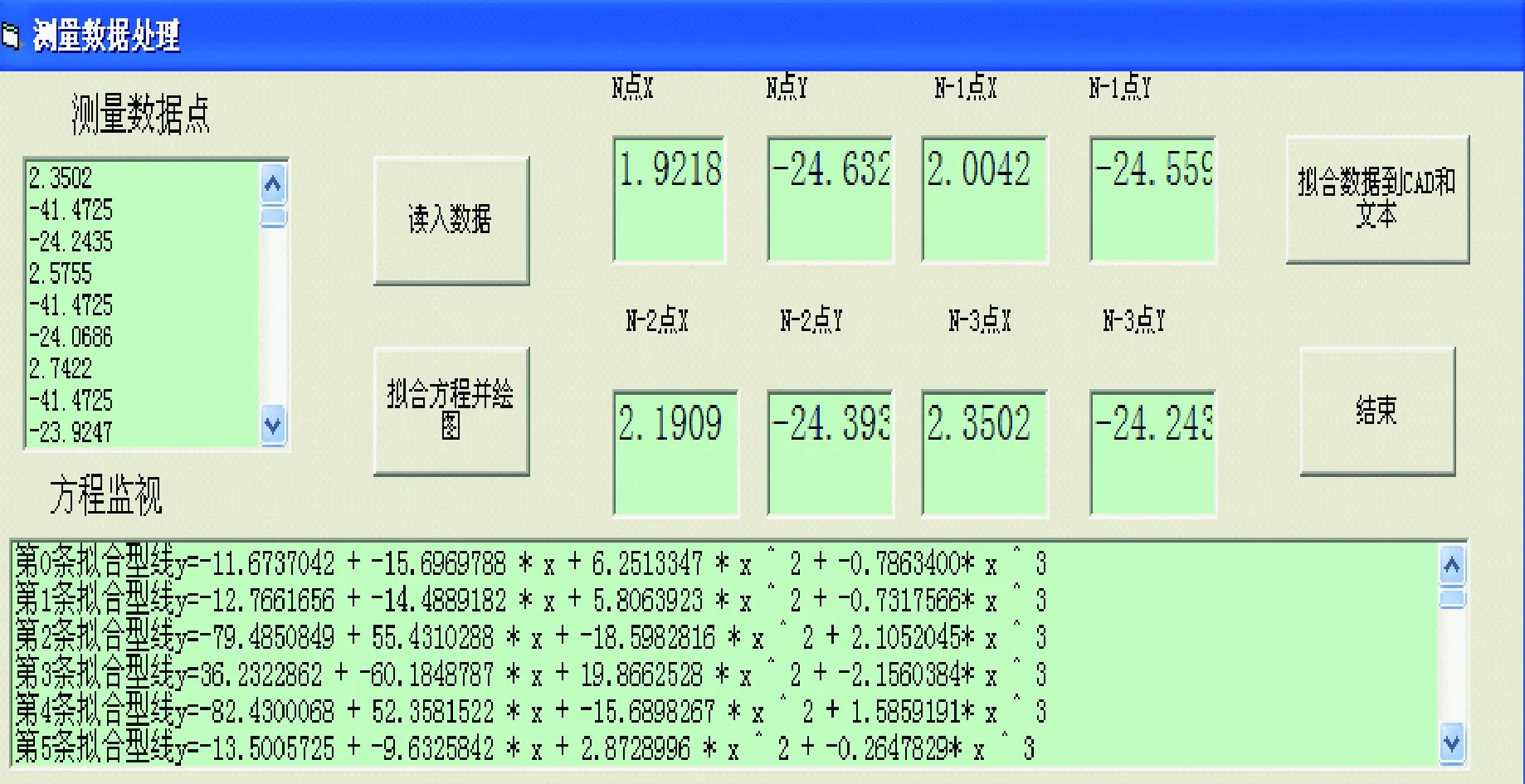
图6 叶片叶型拟合计算界面Fig.6 Interface of fitting calculation of blade profile
从图7可以看出,拟合型线在进口圆处、压力面、吸力面最大弯度位置以前的部分与原设计叶片型线基本吻合,只是在吸力面型线出口段与设计型线相比出现了一些偏离。分析出现偏离的原因认为:由于接触式测量是在零件表面按一定步长选取有限个点测量其坐标,而在吸力面型线出口段曲线曲率较大,为了使测点能够准确描述该段形状,需要更多测点,即减小测量步长,而增加整个叶片的测点会给后面的叶片型线拟合带来更大难度。图7中,原设计叶型的出口圆直径为0.8 mm,拟合叶型出口圆直径为0.2 mm,拟合叶型与原设计叶型在吸力面出口段的偏离不是很大,基本可以满足测量要求。
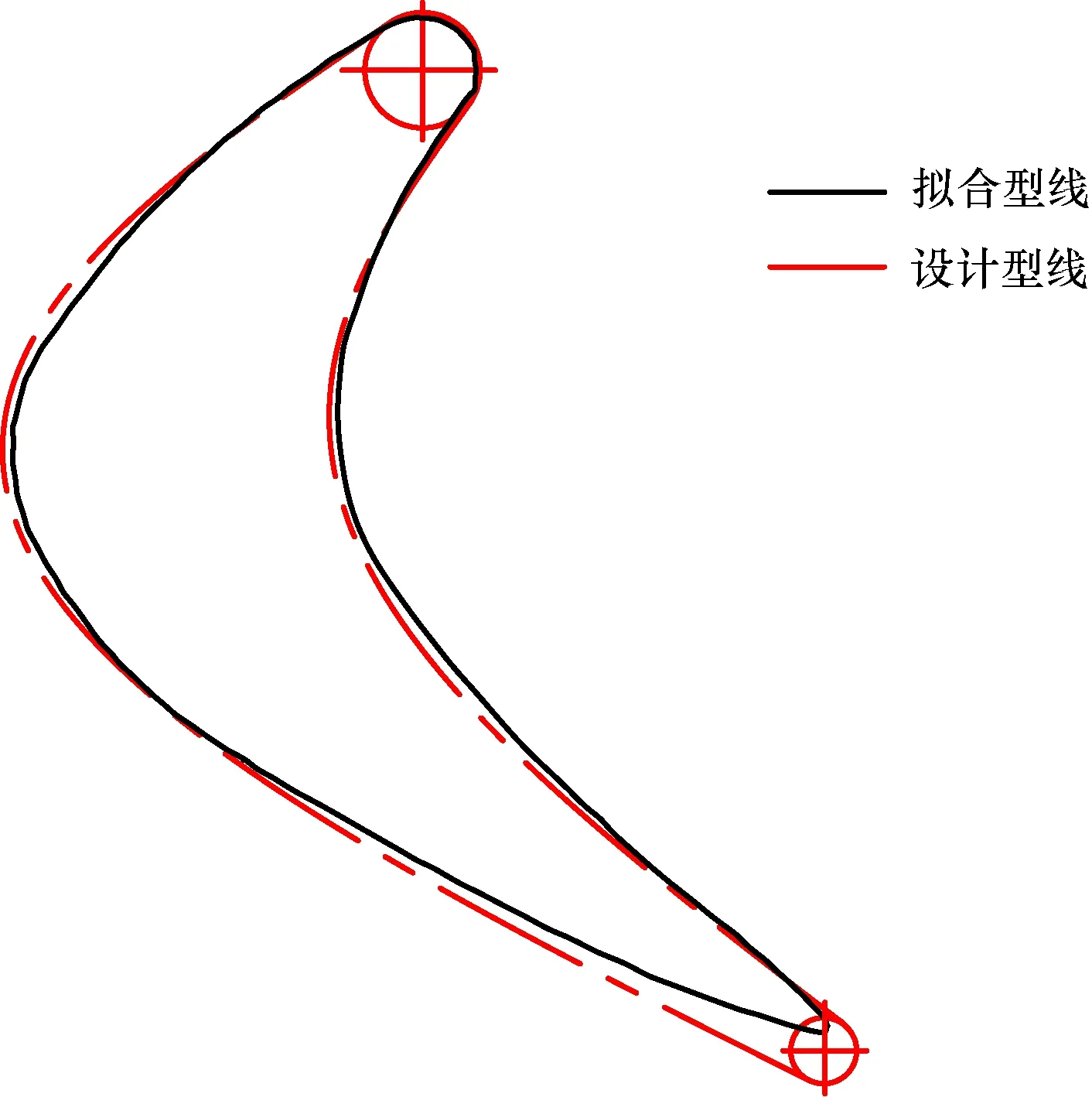
图7 拟合叶片型线与设计叶片型线对比Fig.7 Comparison of fitted blade profile and designed blade profile
综上所述,通过提出的基于三坐标测量机的涡轮钻具叶片叶型测量方法,拟合的叶片型线与原设计型线吻合较好,可基本满足相关测量要求,证明该方法可行。
4 结束语
基于涡轮钻具的定转子结构分析,确定了以接触式测量方式来测量涡轮钻具叶片叶型的方法,提出了以平均水力半径为切割路径来去掉叶片叶冠而获得叶型的技术手段,给出了分别测量吸力面和压力面型线的方法。在测量数据点坐标的基础上,结合流体流动的特点,提出了以点分组控制三次曲线的方法来拟合被测叶片型线,并通过实例分析证明了所提出方法的可行性。当然,目前情况下该方法的总体测量精度还不够高,还有待于进一步分析研究。
参考文献
References
[1] 许福东,张晓东.带同步减速器涡轮钻具工作力学与性能仿真[M].武汉:中国地质大学出版社,2004:2-5.
Xu Fudong,Zhang Xiaodong.Working mechanics and performance simulation of turbodrill with synchronous reducer[M].Wuhan:China University of Geosciences Press,2004:2-5.
[2] 李俊华.高速涡轮节设计与涡轮叶栅流场分析[D].成都:西南石油大学机电工程学院,2010.
Li Junhua.Design of high-speed turbine section and flow field analysis of turbodrill blade[D].Chengdu:Southwest Petroleum University,School of Mechatronic Engineering,2010.
[3] 万军,鞠鲁粤.逆向工程中数据点云精简方法研究[J].上海大学学报:自然科学版,2004,10(1):26-29.
Wan Jun,Ju Luyue.Data reduction for reverse engineering[J].Journal of Shanghai University:Natural Science,2004,10(1):26-29.
[4] 戴静.逆向工程数据处理关键技术研究[D].南京:南京理工大学机械工程学院,2003.
Dai Jing.Key technology research of data processing in reverse engineering[D].Nanjing:Nanjing University of Science & Technology,School of Mechatronic Engineering,2003.
[5] Sobieczky H,Dulikravich G S,Dennis B H.Parameterized geometry formulation for inverse design and optimization:proceeding of 4th International Conference on Inverse Problems in Engineering,Angra dos Reis,Brasil,May 26-31,2002[C].
[6] 冯进,符达良.涡轮钻具涡轮叶片造型设计新方法[J].石油机械,2000,28(11):9-12.
Feng Jin,Fu Daliang.New design method of turbine blade shape of turbodrill[J].China Petroleum Machinery,2000,28(11):9-12.
[7] 陈铁,刘仪,刘斌,等.轴流式叶轮机械叶型的参数设计方法[J].西安交通大学学报,1997,31(5):52-57.
Chen Tie,Liu Yi,Liu Bin,et al.A character-parameter method for axial turbomachinery blade design[J].Journal of Xi’an Jiaotong University,1997,31(5):52-57.
[8] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000:32-42.
Zhu Xinxiong.Freedom curve and surface modeling techniques[M].Beijing:Science Press,2000:32-42.
[9] 白晓亮,张树生.涡轮叶片叶面B-spline曲面层次化拟合方法[J].航空学报, 2009,30(10):1978-1984.
Bai Xiaoliang,Zhang Shusheng.Hierarchical B-spline surface fitting of turbine blades[J].Acta Aeronautica et Astronautica Sinica,2009,30(10):1978-1984.
[10] Shahpar D S.A comparative study of optimization methods for aerodynamic design of turbomachinery blades[R].ASME 2000-GT-523,2000.
