页岩气水平井分段压裂优化设计新方法

蒋廷学, 卞晓冰, 袁 凯, 周林波

(1.中国石化石油工程技术研究院，北京 100101；2.中国石油大学(北京)石油工程学院，北京 102249)

由于页岩裂缝形态复杂，要考虑的因素多[1-4]，因此与常规油气井压裂优化设计相比，页岩气水平井压裂优化设计要更复杂、更困难。目前，页岩气水平井分段压裂设计是在采用常规砂岩水平井分段压裂设计方法的基础上，又应用正交设计原理，对网络裂缝多缝长及多导流能力进行优化[5-6]。实际上，网络裂缝是页岩气水平井压裂设计的最高目标，一般难以实现。多口页岩气水平井压后评估结论认为，网络裂缝形成的概率仅为10%左右，单一裂缝为40%左右，其余的则是介于单一裂缝和网络裂缝之间的复杂裂缝[7-8]。可以这样认为，压裂产生的裂缝形态都是复杂裂缝，单一裂缝和网络裂缝是复杂裂缝的两种特殊表现形式。目前，对于复杂裂缝的表征及压裂优化设计还没有一套成熟的方法。为此，笔者提出了以提高裂缝复杂性指数为目标的页岩气水平井压裂优化设计新方法，针对水平层理缝/纹理缝发育储层及高角度天然裂缝发育储层，给出了分段压裂优化设计方法和流程，以及提高裂缝复杂性指数的技术措施。现场应用实例表明，该方法可以提高页岩气井的压后产量。

1 复杂裂缝的量化表征新方法

文献[9]虽然已对页岩气水平井分段压裂的裂缝复杂性指数进行了量化表征，但仅给出了不同缝间距及缝长条件下裂缝复杂性指数的分布范围，并未就复杂裂缝本身进一步细分。例如，同样是复杂裂缝，有的复杂性指数接近单一裂缝的临界值，而有的裂缝复杂性指数却接近网络裂缝的临界值。因此，泛泛讨论复杂裂缝，忽视了复杂裂缝本身的差异性，对裂缝的复杂程度仍没有清晰的认识，并不能实现压裂设计的最优化。为此，笔者提出了一个新的复杂裂缝量化表征方法。

1.1 裂缝复杂性指数的新定义

水平井分段压裂裂缝如图1所示。图1中，假设分支裂缝1—6相互平行，都垂直于水力裂缝Ⅱ，且对称分布于水力裂缝Ⅱ的全缝长范围内。根据已有裂缝复杂性指数的定义[9]，分支裂缝1—6的平均长度与水力裂缝Ⅱ的全缝长的比值再乘以4因素的叠加因子，其值即为裂缝复杂性指数。该定义认为分支裂缝1—6的渗流干扰波及面积正好相互叠置，但实际上分支裂缝的密集程度可能没有达到将上述渗流干扰波及面积全覆盖的程度。因此，笔者提出裂缝复杂性指数的一个新定义：不同分支裂缝渗流干扰波及面积与水力裂缝Ⅱ的全缝长相除，得到分支裂缝的等效缝宽，该等效缝宽与水力裂缝Ⅱ的全缝长的比值，再乘以4因素的叠加因子，其值即为裂缝复杂性指数。表达式为：

(1)

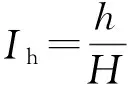
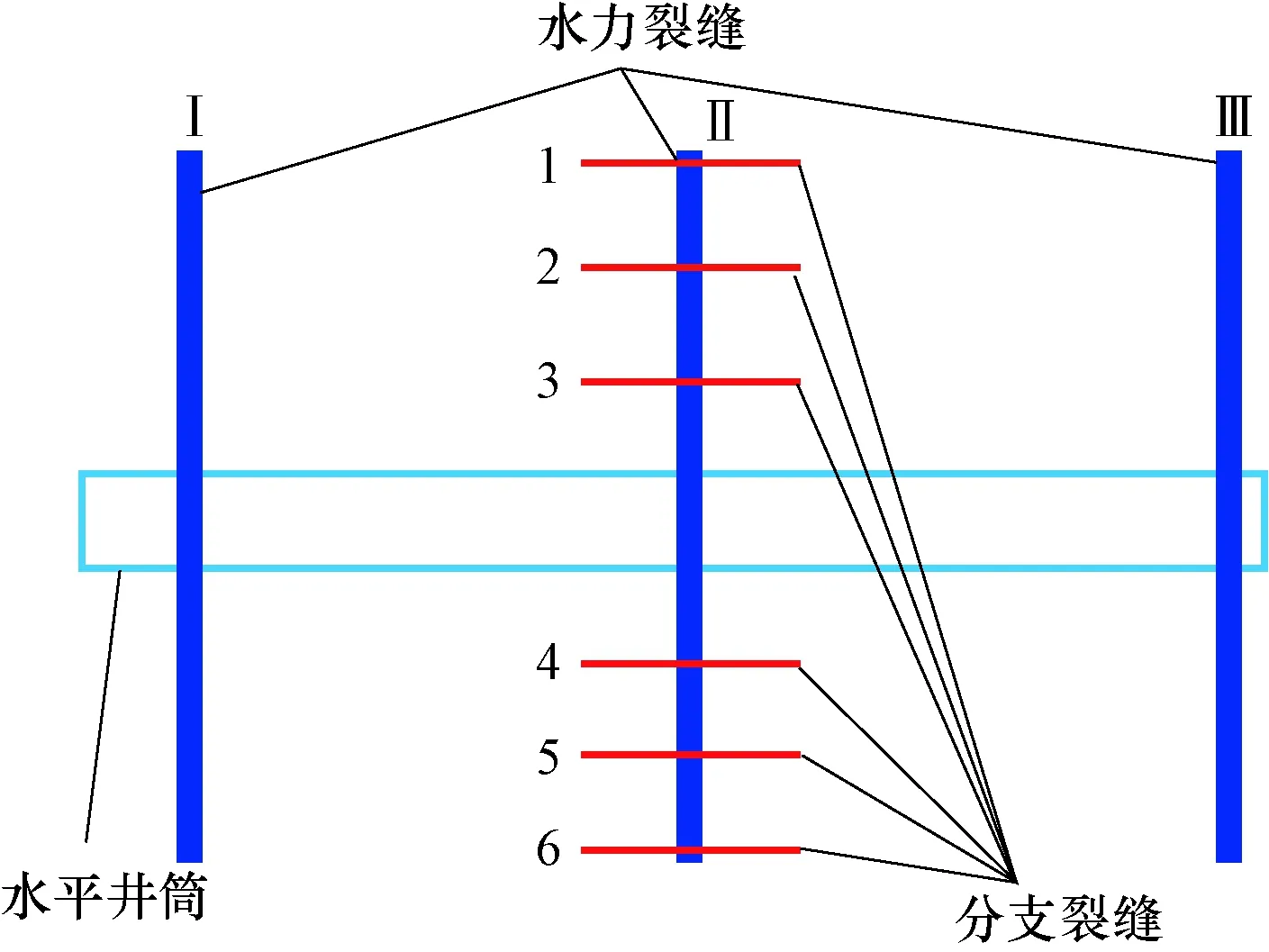
图1 水平井分段压裂裂缝示意Fig.1 Schematic of fractures of staged fracturing horizontal well

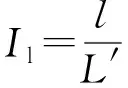
1.2 分支裂缝渗流干扰波及面积的确定

如果完全按渗流干扰理论，页岩基质的超低渗透性会导致渗流影响的区域非常有限。为此，笔者认为可以将应力干扰区叠加面积近似视为分支裂缝的渗流干扰波及面积。在计算应力干扰区叠加面积时，首先计算水力裂缝Ⅱ的诱导应力传播区域，再分别计算分支裂缝1—6的诱导应力传播区域，2个传播区域的叠加面积，即为应力干扰区叠加面积。如果水力裂缝Ⅱ的传播距离超过分支裂缝1—6的半缝长，可以用原始水平应力差为界来压缩水力裂缝Ⅱ的诱导应力传播距离。此外，如果分支裂缝净压力太小，其诱导应力传播距离实在有限，可以不考虑以水平应力差(此水平应力差非原始水平应力差，而是考虑了水力裂缝Ⅱ已经产生的诱导应力)为界，而直接计算水力裂缝Ⅱ与分支裂缝1—6的渗流干扰波及面积。

1.3 分支裂缝的分布及延伸长度的确定

由前期裂缝扩展物模试验结果可知[10]，水力裂缝Ⅱ在扩展过程中，遇到天然裂缝的表现是压力曲线呈现锯齿状波动。出现压力波动的时机反映出分支裂缝距离水平井筒的远近，压力波动的幅度及波幅的宽度反映了分支裂缝的长度及宽度。利用压裂施工综合曲线，可以近似计算出每个分支裂缝延伸的用液量(约等于波幅宽度对应的时间与注入排量的乘积)。至于分支裂缝的排量分配，目前还没有可靠的方法，可以假设为注入排量的1/10～1/5，并且假设分支缝的端部净压力低于临界应力强度因子后，分支裂缝不再继续延伸。按照同样的方法，可以计算出水力裂缝Ⅱ遇到第2个分支裂缝后，第2个分支裂缝的长度及宽度。两个相邻分支裂缝的距离，可以依据压裂施工参数，通过成熟的商业软件(如MEYER等)模拟计算得出。至此，可计算出各分支裂缝沿水力裂缝Ⅱ全缝长方向的分布，以及每个分支裂缝的长度及宽度。

将分支裂缝的渗流干扰波及面积及其长度、宽度以及其他已知参数，代入式(1)即可计算出裂缝复杂性指数。

2 压裂优化设计方法

笔者采用ECLIPSE软件(具备模拟吸附气的功能模块)，按图1所示设置了不同复杂性指数条件下的水力裂缝与分支裂缝分布，对压裂后形成不同形态裂缝的产量动态进行了模拟计算，结果见图2。理论上讲，裂缝复杂性指数越高，压后产量越高，但从图2可以看出，一般很难找到裂缝复杂性指数的拐点值。换言之，压裂优化设计的目标就是在已有施工条件的前提下，最大限度地提高裂缝复杂性指数。

图2 不同裂缝复杂性指数下页岩气水平井压后3年累计产气量模拟计算结果Fig.2 3 years cumulative gas production of fractured horizontal shale gas well with different fracture complex index

2.1 水平层理缝/纹理缝发育储层

在压裂水平层理缝/纹理缝发育储层时，水力裂缝即使不能沟通全部的层理缝/纹理缝，也能在一定程度上沟通层理缝/纹理缝。这与图1中的分支裂缝情况不同，因二者的方向刚好相差90°。一般情况下，层理缝/纹理缝的存在是页岩的重要特征，且呈多层叠置分布，它对水力裂缝缝高的增长具有较强的遏制作用，常规砂岩或碳酸盐岩的垂向应力差遮挡的概念在很大程度上已不适用。

目前，室内试验已证实，当遇到水平层理缝/纹理缝时，水力裂缝能很快沟通并使其延伸。但由于受试验排量的限制，还未发现水力裂缝接着穿越第2条层理缝/纹理缝的情况。根据能量守恒原则，当水力裂缝穿越第1条层理缝/纹理缝后，由于消耗掉很大一部分能量，已再无能量穿越另外的层理缝/纹理缝。或者，虽有后续能量的不断补充，但层理缝/纹理缝一旦被沟通，由于其处于地质力学上的弱面，能量大部分被已延伸的层理缝/纹理缝吸收并继续延伸。实际上，最理想的情况是不同的层理缝/纹理缝都能被依次打开并且都能最大限度地得到延伸，最终形成体积裂缝。为此，可先设计低黏度滑溜水打开第1条层理缝/纹理缝，等延伸到预期的缝长后，再注入高黏度胶液(线性胶或交联冻胶)，并尽最大可能提高注入排量，以尽可能打开第2条层理缝/纹理缝，然后再注入低黏度滑溜水，由于黏度差发生的黏滞指进效应，滑溜水会很快穿过高黏度胶液，在新打开的层理缝/纹理缝里继续延伸。依次类推，最终实现所有层理缝/纹理缝都被打开并被充分延伸的目的。

滑溜水与胶液的注入比例、具体注入体积、排量等参数，要采取循序渐进的原则。换言之，胶液的体积及排量宜小不宜大，以防止一次就打开所有层理缝/纹理缝。但也不能太小，太小可能就难以压开第2条层理缝/纹理缝。

理论分析认为，先用高黏度胶液一次将所有层理缝/纹理缝全部压开，然后换用低黏度滑溜水同时延伸所有已压开的层理缝/纹理缝的设计思路，实现难度较大，因为如果多个水平层理缝/纹理缝同时延伸的话，其延伸阻力会非常大，而在垂向上还有两翼主裂缝在与它们争夺注入的压裂液，显然两翼主裂缝更易吸收大量的压裂液，因其流动阻力毕竟要相对小很多。

因施工现场面临操作上的一些难题，目前在压裂水平层理缝/纹理缝比较发育的储层时，大多只简单地用高黏度胶液，争取先把它们全部压开。随着理论的进一步完善和现场实践经验的不断丰富，随着技术水平的日益提高，会逐步实现上述目标。

2.2 高角度天然裂缝发育储层

在遇到高角度天然裂缝发育储层时，首先要判断该裂缝是张开型还是潜在型(或充填型)。

对于张开型高角度天然裂缝，为了降低压裂液滤失量，应当尝试粉陶与常规大粒径支撑剂混合的施工方法，即在遇到张开型天然裂缝后，将粉陶按一定比例和大粒径支撑剂混合，一起注入裂缝中，因小粒径粉陶的流动阻力小，会优先进入裂缝，而大粒径支撑剂因流动阻力大，很难进入天然裂缝，而且天然裂缝的张开宽度可能也不足以使其进入。粉陶用量与天然裂缝发育程度密切相关，最理想的结果是所有粉陶都进入天然裂缝中，所有的大粒径支撑剂都留在人工主裂缝中，但由于天然裂缝的分布情况很难准确预测，因而粉陶用量的设计不可能达到最优。但开始压裂时可先采用小比例粉陶，在压裂施工过程中不断优化加量，逐步摸索出最佳的混合比例。先前技术人员对天然裂缝有一种先入为主的偏见，即遇到天然裂缝就快速封堵，不让其延伸。随着人们对裂缝复杂性指数认识的不断深入，认为有必要先延伸天然裂缝，然后再实施封堵，可以采取延缓粉陶的注入时机和/或降低粉陶加量等办法来达到该目的。

对潜在型(或充填型)天然裂缝，可先计算其临界张开压力，如果临界张开压力很大，而主裂缝净压力又相对较小，则天然裂缝在整个压裂施工过程中是不能张开的。反之，如果临界张开压力很小，在压裂施工过程中天然裂缝会过早张开，使主裂缝的缝长难以达到设计要求。因此，在该情况下，压裂初期就要优选施工参数(液量、排量、黏度、砂浓度等)，以有效控制主裂缝净压力小于天然裂缝的临界张开压力，等主裂缝的缝长达到设计要求后，再优选施工参数以提高主裂缝净压力，使天然裂缝张开，最终形成沟通近井、远井微裂缝系统的网络裂缝，达到最大限度提高改造体积的目的。

天然裂缝临界张开压力计算公式为：

(2)

式中：pc为天然裂缝临界张开压力，MPa；σmax，σmin分别为最大和最小水平主应力，MPa；ν为泊松比。

2.3 天然裂缝分布密度及延伸缝长的定量描述方法

天然裂缝分布密度的计算相对容易，可将现场压裂施工的井口压力曲线转变为井底压力曲线，再根据压力曲线的波动情况，结合相关裂缝模拟软件，识别在主裂缝缝长方向上的天然裂缝分布密度。

主裂缝穿过天然裂缝有以下3种情况：

1) 主裂缝遇到张开型天然裂缝。当主裂缝遇到第1条天然裂缝时，压裂液会发生分流，但大部分压裂液仍在主裂缝内。由于天然裂缝缝宽小，压裂液流动阻力大，在不长时间内裂缝就会停止延伸。当主裂缝遇到第2条天然裂缝时，又发生上述同样的现象，依此类推。

2) 主裂缝遇到潜在型(或充填型)天然裂缝，净压力未控制好。在这种情况下，天然裂缝会过早张开，这与第一种情况类似，不再赘述。

3) 主裂缝遇到潜在型(或充填型)天然裂缝，但净压力控制好。在这种情况下，直到主裂缝的缝长达到预期要求时，才让所有的天然裂缝张开。由于多个天然裂缝同步张开，相互间竞争压裂液，因而与前两种情况相比，天然裂缝延伸范围会较大幅度缩小，这与限流压裂的分流情况类似。

描述每条天然裂缝的缝长及缝宽的一个重点就是确定流量在各裂缝的动态分配，多条裂缝同时存在和延伸时满足Kirchoff第一定律和第二定律，即物质平衡和压力连续准则。对主裂缝穿过天然裂缝的3种情况建立数学模型，可计算不同液量及排量条件下每条天然裂缝的缝长及缝宽，即可定量确定裂缝复杂性指数。

2.3.1 第一和第二种情况下的裂缝扩展模型

第一、第二种情况下，随着压裂施工的进行，天然裂缝的张开数量逐渐增加，即参与分流的裂缝数量增加。假设在j-1 时刻，主裂缝延伸至第k+1条天然裂缝且天然裂缝开始张开，则第k+1条天然裂缝的缝口压力为缝口闭合压力σc,k+1，裂缝扩展模型为：

(3)

p0=Δpcfi+Δpwi+σni=Δpcf,k+1+σc,k+1

(4)

(5)

pwi,xi=pcfi

(6)

(7)

(8)

pcf,xk+1=σc,k+1

(9)

pcf,x0=p0

(10)

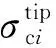
随后的时间段，仍然只有k+1条天然裂缝，则裂缝扩展模型为：

(11)

p0=Δpcfi+Δpwi+σni

(12)

(13)

pwi,xi=pcfi

(14)

(15)

(16)

pcf,x0=p0

(17)

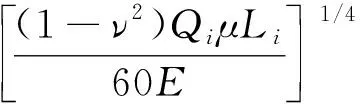
(18)

(19)

(20)

(21)

式中：i=1,2,…,k+1。

2.3.2 第三种情况下的裂缝扩展模型

第三种情况下，假设各天然裂缝同时开启和进液，则裂缝扩展模型为：

(22)

p0=Δpcfi+Δpwi+σni

(23)

(24)

pcf,inlet=p0

(25)

(26)

pwi,inlet=pcfi

(27)

(28)

式中：pwi,inlet为第i条天然裂缝的缝口压力，MPa。

各个天然裂缝的缝宽与缝长计算公式与式(18)—(21)相同。

2.4 提高裂缝复杂性指数的技术措施

由式(3)～(28)可知，要提高裂缝复杂性指数，关键是尽可能增大天然裂缝的缝长和缝宽。如有可能，应使主裂缝的转向次数更多。在纵向上，尽可能多地压开所有的层理缝/纹理缝，并让其最大限度地得到延伸。由此，可在纵横向上最大限度地提高裂缝的改造体积，实现压裂效果的最优化。

延伸天然裂缝的主要技术措施：一是要降低压裂液的黏度，使其尽可能多地进入天然裂缝，促使天然裂缝尽可能延伸，可通过模型计算延伸的缝长及缝宽；二是控制粉陶的加砂时机及加量、段塞量等，目前还无法实现定量模拟。

促使主裂缝多次转向的主要技术措施：由于主裂缝内存在压力梯度，压力梯度越小，主裂缝转向的概率越大，可采用低黏度压裂液和降低排量等措施来降低主裂缝内的压力梯度；另外，要最大限度地提高主裂缝的净压力，除了可以优化压裂液黏度、液量、排量及施工砂液比等参数外，还可以采用人工转向技术，如应用缝内暂堵剂等。

3 应用实例

涪陵焦石坝区块A井和B井2口页岩气井位于同一平台，其水平段长度、压裂段数及施工压力都比较接近，两井施工参数见表1，压裂施工曲线如图3所示。其中，B井压裂设计采用了笔者提出的新方法，A井使用常规方法。

表1焦石坝区块2口页岩气井施工参数

Table1Constructionparametersof2horizontalshalegaswellsinJiaoshibaArea

井名水平段长/m段数/簇数施工压力/MPa停泵压力/MPaA井1 00815/3650～5731B井1 00315/3650～7028

根据笔者提出的压裂设计新方法，增大液量和排量是提高裂缝复杂性指数的有效措施，因此与A井相比，B井的单段施工液量约高214 m3，排量高2～3 m3/min。根据式(1)计算得到A井的裂缝复杂性指数为0.13，B井的裂缝复杂性指数为0.16，2口井压后无阻流量分别为16.74×104和21.18×104m3/d(见表2)，产量约提高26%。由此可见，采用笔者提出的新方法对压裂施工参数(排量和液量等)进行优化后，气井的裂缝复杂性指数及压后产量都得到了明显提高。

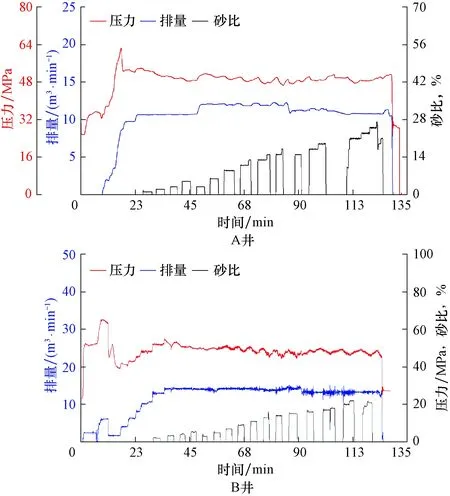
图3 A井和B井压裂施工曲线Fig.3 Hydrofracture construction curve of Well A and well B

4 结论与建议

1) 考虑了各分支裂缝沿主水力裂缝方向的分布密度及其相互间的渗流干扰波及面积，提出了新的裂缝复杂性指数表达式，使其不仅仅是一个范围，而是一个具体数值。

2) 初步建立了以最大限度提高裂缝复杂性指数为目标的页岩气水平井分段压裂优化设计新方法。

3) 现场应用实例表明，提出的压裂优化设计新方法能较大幅度地提高裂缝复杂性指数和压裂后的产量。

4) 建议对水力裂缝与层理缝/纹理缝及天然裂缝的相互干扰及扩展互动情况进行三维模拟分析，并尽量与相应的物理模拟相结合，以完善页岩气水平井分段压裂优化设计方法。

表2 焦石坝区块2口页岩气井裂缝复杂性指数及无阻流量Table 2 Fracture complex index and open flow capacity of 2 horizontal shale gas wells in Jiaoshiba Area

参考文献
References

[1] Rickman R,Mullen M,Petre E,et al.A practical use of shale petrophysics for stimulation design optimization:all shale plays are not clones of the Barnett shale[R].SPE 115258,2008.

[2] Wang Y,Miskimins J L.Experimental investigations of hydraulic fracture growth complexity in slick water fracturing treatments[R].SPE 137515，2010.

[3] 蒋廷学,贾长贵,王海涛,等.页岩气网络压裂设计方法研究[J].石油钻探技术,2011,39(3)：36-40.

Jiang Tingxue,Jia Changgui,Wang Haitao,et al.Study on network fracturing design method in shale gas[J].Petroleum Drilling Techniques,2011,39(3)：36-40.

[4] 赵金洲，王松，李勇明.页岩气藏压裂改造难点与技术关键[J].天然气工业，2012，32(4)：46-49.

Zhao Jingzhou,Wang Song,Li Yongming.Difficulties and techniques in the fracturing treatment of shale gas reservoirs[J].Natural Gas Industry,2012，32(4)：46-49.

[5] 吴奇,胥云,王腾飞,等.增产改造理念的重大变革：体积改造技术概论[J].天然气工业，2011，31(4)：7-12.

Wu Qi,Xu Yun,Wang Tengfei,et al.The revolution of reservoir stimulation:an introduction of volume fracturing[J].Natural Gas Industry,2011,31(4)：7-12.

[6] Beugelsdijk L J L,Pater C J,Sato K,et al.Experimental hydraulic fracture propagation in a multi-fractured medium[R].SPE 59419,2000.

[7] 曾雨辰，杨保军，王凌冰.涪页HF-1井泵送易钻桥塞分段大型压裂技术[J].石油钻采工艺，2012，34(5)：75-79.

Zeng Yuchen,Yang Baojun,Wang Lingbing.Large-scales staged fracturing technology with pump-down drillable bridge plug for Well Fuye HF-1[J].Oil Drilling & Production Technology,2012,34(5)：75-79.

[8] Soliman M Y,East L,Augustine J.Fracturing design aimed at enhancing fracture complexity[R].SPE 130043,2010.

[9] 蒋廷学.页岩油气水平井压裂裂缝复杂性指数研究及应用展望[J].石油钻探技术，2013，41(2)：7-12.

Jiang Tingxue.The fracture complexity index of horizontal wells in shale oil and gas reservoirs[J].Petroleum Drilling Techniques,2013,41(2)：7-12.

[10] 张旭,蒋廷学,贾长贵,等.页岩气储层水力压裂物理模拟试验研究[J].石油钻探技术，2013，41(2)：70-74.

Zhang Xu,Jiang Tingxue,Jia Changgui,et al.Physical simulation of hydraulic fracturing of shale gas reservoir[J].Petroleum Drilling Techniques,2013，41(2)：70-74.