含沙水下粒径对螺旋离心泵磨蚀效应的数值分析
2014-09-04辉1李仁年1苏清苗
权 辉1,李仁年1 , 苏清苗
(1.兰州理工大学能源与动力工程学院,甘肃 兰州730050;2.甘肃蓝科石化高新装备股份有限公司,甘肃 兰州 730070)
在自然界中,水流经常夹带着悬浮的泥沙、固体颗粒及其他杂质,成为自然界水流运动最普遍的现象[1]。这使得在含沙量比较大的河流运行的流体机械长期受到泥沙冲击而产生汽蚀和磨蚀效应,其使用寿命大大减少。杂质泵中性能优越的螺旋离心泵,是一种把螺旋泵与离心泵2者的优势融合为一体的固液两相流泵,其独特的结构可将2者的优势充分发挥,螺旋离心泵的结构如图1所示。
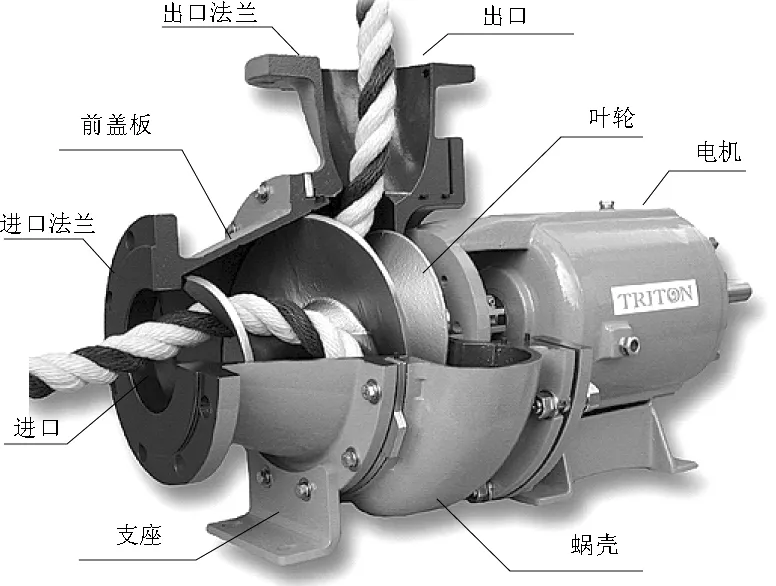
图1 螺旋离心泵结构图
国外对杂质泵磨损规律的研究较早,做过大量的基础性试验和理论分析等工作。日本的Yoshiro Jwai等[2]在不同的实验条件下,给出了计算磨蚀损失的经验公式,Craig I. Walke等[3]通过实验得出了磨损对主要参数影响的经验公式。在国内,罗先武[4]、田爱民等[5]为研究叶片参数、颗粒浓度、叶轮转速以及叶片数对磨损的影响,采用了失重法、磨损量测法和表面涂层法等。在螺旋离心泵内部,由于固相和液相的密度不同,导致产生滑移速度,这不但影响了泵的水力性能,而且容易使固体颗粒容易和过流表面冲突造成泵过流部件的磨损等问题,如果磨损严重的话常常使得泵腔内的汽蚀性能大大降低,进一步恶化其内部流动情况。图2是甘肃兴堡川引黄灌泵站叶轮运行6个月后的磨损状况,可以看出磨损是非常严重的。因此,磨蚀效应仍然是含沙河流中流体机械长久稳定和安全运行所要解决的主要问题。

图2 双吸泵检修叶轮磨蚀状况
1 泥沙磨蚀机制
1.1 泥沙磨蚀机制
关于对磨蚀机制的研究,长期以来都有争论。第1种理论是先空蚀后泥沙磨损,第2种理论是先泥沙磨损,后才产生空蚀破坏,还有1种理论是泥沙磨损与空蚀2者联合作用的结果,作者更认同最后一种说法。本文就含沙水颗粒粒径对螺旋离心泵磨蚀作一定的研究。
1.2 颗粒磨蚀模型
采用数值模拟方法探究螺旋离心泵在含沙水下的磨蚀情况,选用离散相模型,在所有的壁面监视颗粒的磨蚀与沉积情况,其中磨蚀速率[6]定义为
(1)
式中:N为颗粒数;m为颗粒质量流率;C(d)为颗粒直径的函数;a为颗粒对壁面的冲击角;f(a)为 冲击角函数;v为颗粒相对于壁面速度;b(v)为相对速度函数;A为颗粒在壁面上的投影面积。
2 模型建立及数值方法
2.1 模型泵的参数及网格划分
选用150×100LN-32型螺旋离心泵建立模型,其各项性能参数为:流量Q=165 m3/h,扬程H=32 m,转速n=1 480 r/min,轴功率P=23.2 kW。
将整个计算区域按特性分为3段,由2个耦合面来处理动静干涉,进口段和蜗壳采用结构网格,叶轮旋转域采用贴合性较好的非结构四面体网格,整个流道网格节点总数为89 403,单元总数为507 886,并进行了网格无关性检查,整机计算域和网格如图3所示。
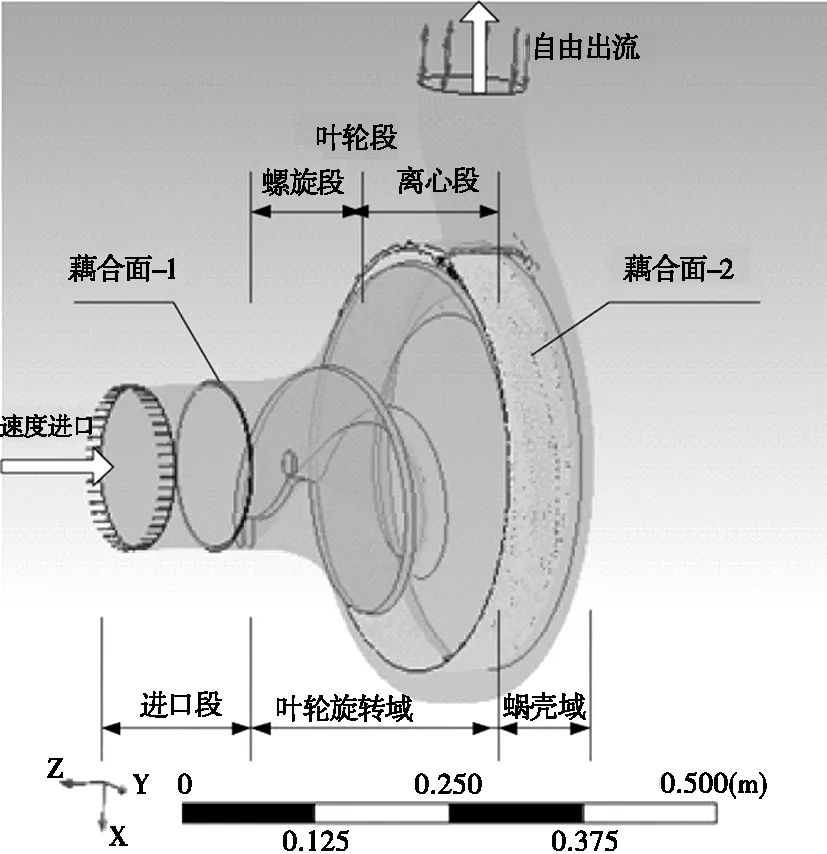
(a)边界示意图

(b)网格划分
2.2 数值方法
对于输送含沙水,选用DPM模型和k-ε湍流模型,流体为清水(water),固相沙粒(sand)作为惰性颗粒。其中,DPM模型中进口设置为质量流率以面射流源形式进入整个计算域,旋转区域的离散相边界为弹性反射。为保证解的收敛性,引入亚松驰因子,经试算,选用压强项亚松弛系数为0.3,动量项亚松弛系数为0.1,紊动能亚松弛系数为0.05,耗散率亚松弛系数为0.05时,可得到收敛解[7-8]。当模拟两相耦合过程时,首先计算得到收敛或部分收敛的连续相流场,然后再创建固相喷射源进行耦合计算。
3 数值模拟结果与分析
由于叶轮是螺旋离心泵的主要做功部件,也是最易因磨蚀而破坏的部件,因此文中选用流体介质为黄河含沙水,固体密度为2 650 kg/m3,在最优工况下运行时一般固相体积分数约为5%;选用颗粒大小分别为0.076 、0.5 、1 mm对叶轮域的磨蚀情况进行了数值模拟,模拟结果及分析如下。
3.1 颗粒体积浓度变化
图4为颗粒大小分别为0.076、0.5、1 mm下的叶轮域的固相体积浓度分布云图。

(a)d=0.076 (b)d=0.5

(c)d=1
由图4(a)、(b) 和 (c)叶轮浓度分布可以看出,浓度分布比较紊乱,叶片背面外缘处浓度分布明显高于靠轮毂侧的浓度分布,工作面在螺旋段进口部分和离心段出口部分外缘浓度分布高于靠轮毂侧浓度分布,其他部分浓度相差不大,小颗粒没有往轮毂聚集的趋势,这与国内对颗粒运动轨迹的研究结论一致。
3.2 叶轮域速度变化
叶轮表面的法向速度对叶轮主要是冲击破坏,切向速度对叶轮表面主要是磨蚀破坏,工作面为叶轮做功面。图5为粒径0.5 mm时的固相沿工作面轮缘、轮毂的速度变化。

(a) 法向速度变化
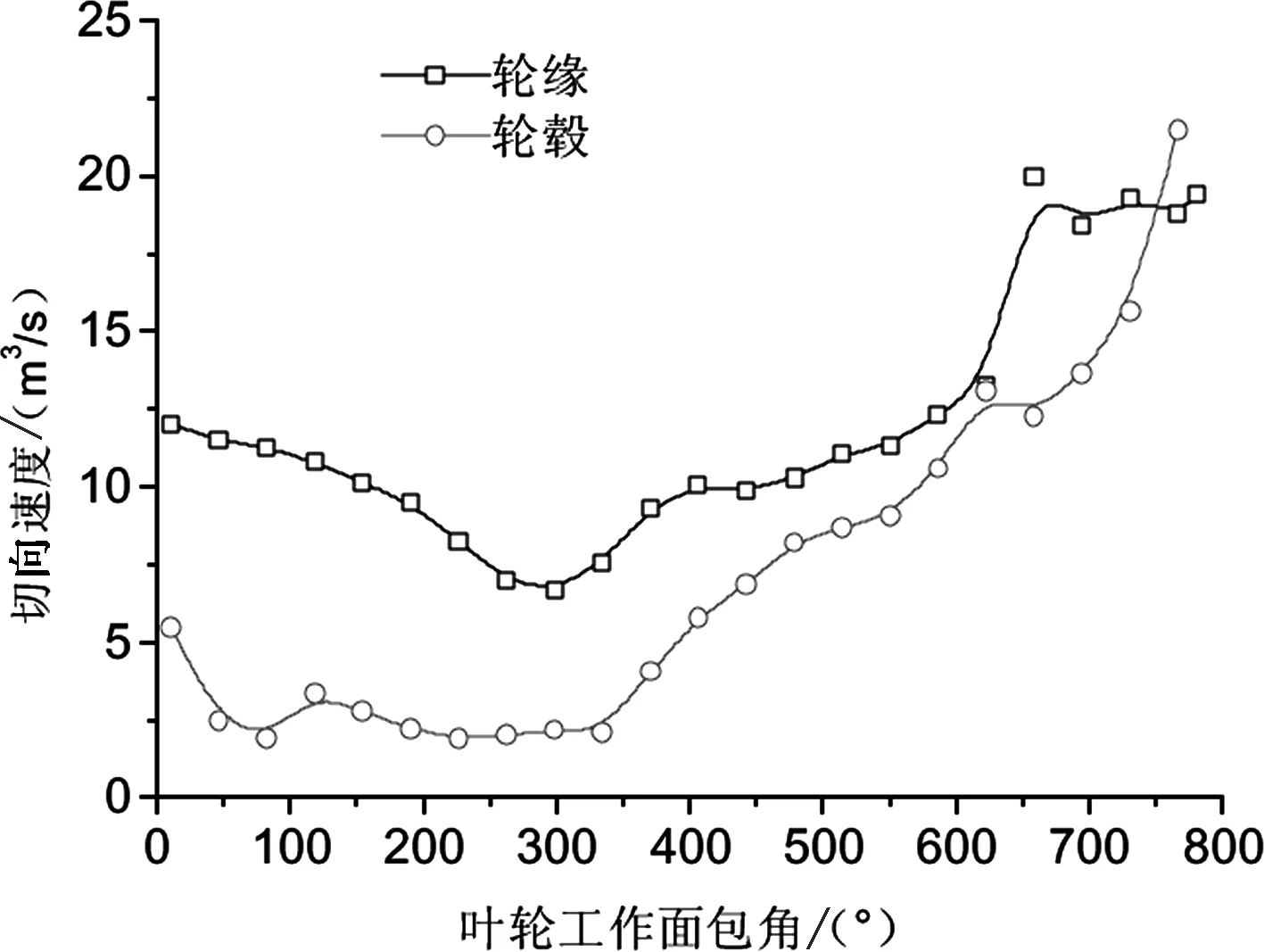
(b)切向速度变化
由图5(a)和(b)可以看出:无论是法向速度还是切向速度,沿叶轮工作面的轮缘处的速度整体上大于轮毂处,这说明磨蚀在轮缘处要比轮毂处更容易发生;对比叶轮同一位置可以看出,无论在轮缘还是轮毂,切向速度整体大于法向速度,也就是说在冲击磨损和磨蚀中,切向速度的大小决定了磨蚀的程度。下面就不同颗粒粒径下的磨蚀进行分析。
3.3 磨蚀云图
在FLUENT软件中,DPM模型中参数Erosion Rate是对磨蚀程度衡量的一个重要参数,单位为kg/(m2·s)。图6为颗粒大小分别为0.076 、0.5、1 mm下的叶片域的Erosion Rate变化云图。

(a)d=0.076

(b)d=0.5
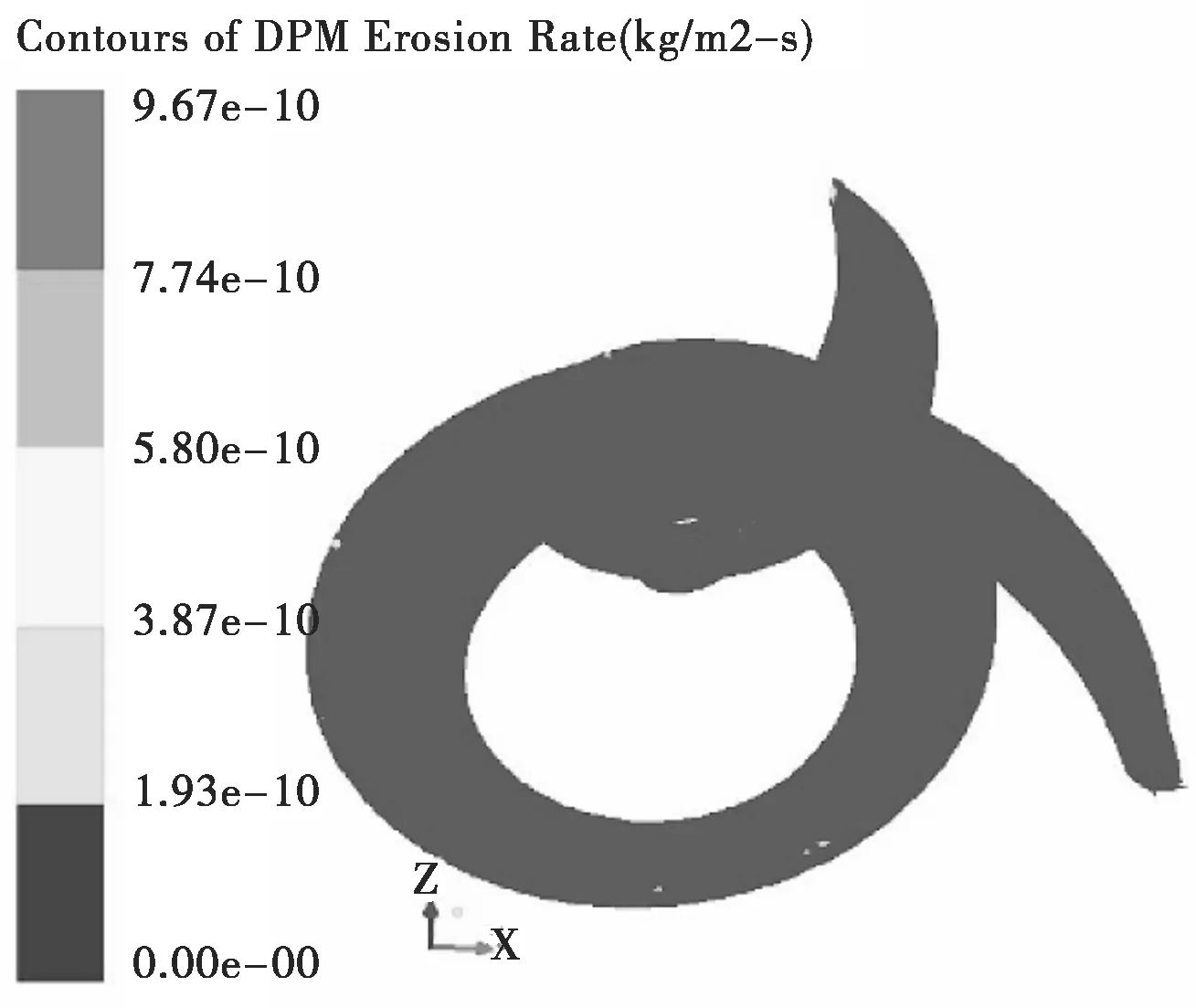
(c)d=1
由图6(a)、(b)和(c)叶片的磨蚀云图可以看出:粒径分别为0.076、0.5、1 mm时,叶片域的磨蚀云图变化基本一致,说明了粒径对叶轮的磨蚀局域变化影响不大;从磨蚀指标Erosion Rate可以看出,粒径越大,磨蚀指标Erosion Rate越大,也就是说粒径决定了磨蚀的程度。
综合体积浓度变化和磨蚀指标来看,粒径越大,颗粒在叶片轮缘聚集越多,浓度体积梯度越大,对轮缘的磨蚀比靠轮毂侧的严重。同时,粒径越大,在模拟中并不是磨蚀越明显,通过分析可知,磨蚀是多因素综合决定的,除了粒径之外,还与颗粒的硬度、速度、冲击角等有关。
4 结论
1) 颗粒粒径对颗粒运动轨迹的影响较大,颗粒粒径越大,越偏向叶片的轮缘,对轮缘的破坏越严重;
2) 对于同一种颗粒,由于粒子比重一样,在叶轮作用下,颗粒大对叶轮的冲击越大。同时,形成体积浓度的梯度不均匀,更加剧了磨损的破坏程度;
3)磨蚀是一个综合作用的共同效应,本文只是从固相粒径的方面进行一定的探究,还有待进一步研究固相多因素对磨蚀的影响。
[1]吴玉林.水力机械空化和固液两相流体动力学[M].北京:中国水利水电出版社,2007:1-6.
[2]Yoshiro Jwai, Kazuyuki Nambu. Slurry Wear Properties of Pump Lining Materials[J].Wear,1997,210:211-219.
[3]Craig I Walker, Greg C Bodkin. Empirical Wear Relationships for Centrifugal Pumps Part Ⅰ: side-lines[J]. Wear 242, 2000:140-146.
[4]罗先武.离心泵叶轮内磨损规律的实验研究[D]. 北京:清华大学,1996.
[5]田爱民,许洪元,罗先武,等.离心式渣浆泵叶轮的磨损规律研究[J].水泵技术,1997(6):7-10.
[6]赵新学,金有海,孟玉青,等. 旋风分离器壁面磨损的数值分析[J]. 流体机械, 2010, 38(4):18-22.
[7]李仁年,齐学义,张建华.用能耗极值原理模拟水轮机内含沙水流的数学模型[J].动力工程,2003,19(5):399-402.
[8] Wu Yulin,Oba R,Ikohagi T. Computation on Turbulent Dilute Liquid-panicle Flows through a Centrifugal Impeller[J]. Japanese J Multiphase Flow,2004,8(2):118-125.
