平面二次包络环面蜗杆数控加工误差分析研究

(四川工程职业技术学院，四川 德阳 618000)

平面二次包络环面蜗杆副是20世纪70年代由我国首创的一种优良传动副[1]。作为一种可靠的重载传动副，它具有承载能力强、传动效率高、使用寿命长等优点，广泛应用于冶金矿山机械、化工硫化机械、军舰和船舶甲板机械[2]。虽然平面二次包络环面蜗杆副是我国的原创技术，但是加工高精度蜗杆副比较困难；所以，国内平面二次包络环面蜗杆传动与国外的类似蜗杆传动产品相比还是存在较大差距[3-10]。在机械加工中，机床加工精度最终是由刀具与工件间的相对位移决定的，刀具与工件间的误差可用误差数学模型来表示。本文根据多体系统理论及运动副的误差运动学原理对包含2个移动副和2个转动副并考虑几何误差和热误差等共计37个误差元素的四轴数控蜗杆加工机床建立空间几何误差模型[3]。

1 理论基础

第1次包络过程的坐标设置如图1所示。Sj为蜗杆的静坐标系。S1为与蜗杆固联的动坐标系。S0为工作台的固定坐标系，也即蜗轮的静坐标系。S2为与工作台一起转动的动坐标系即蜗轮的动坐标系[4]。

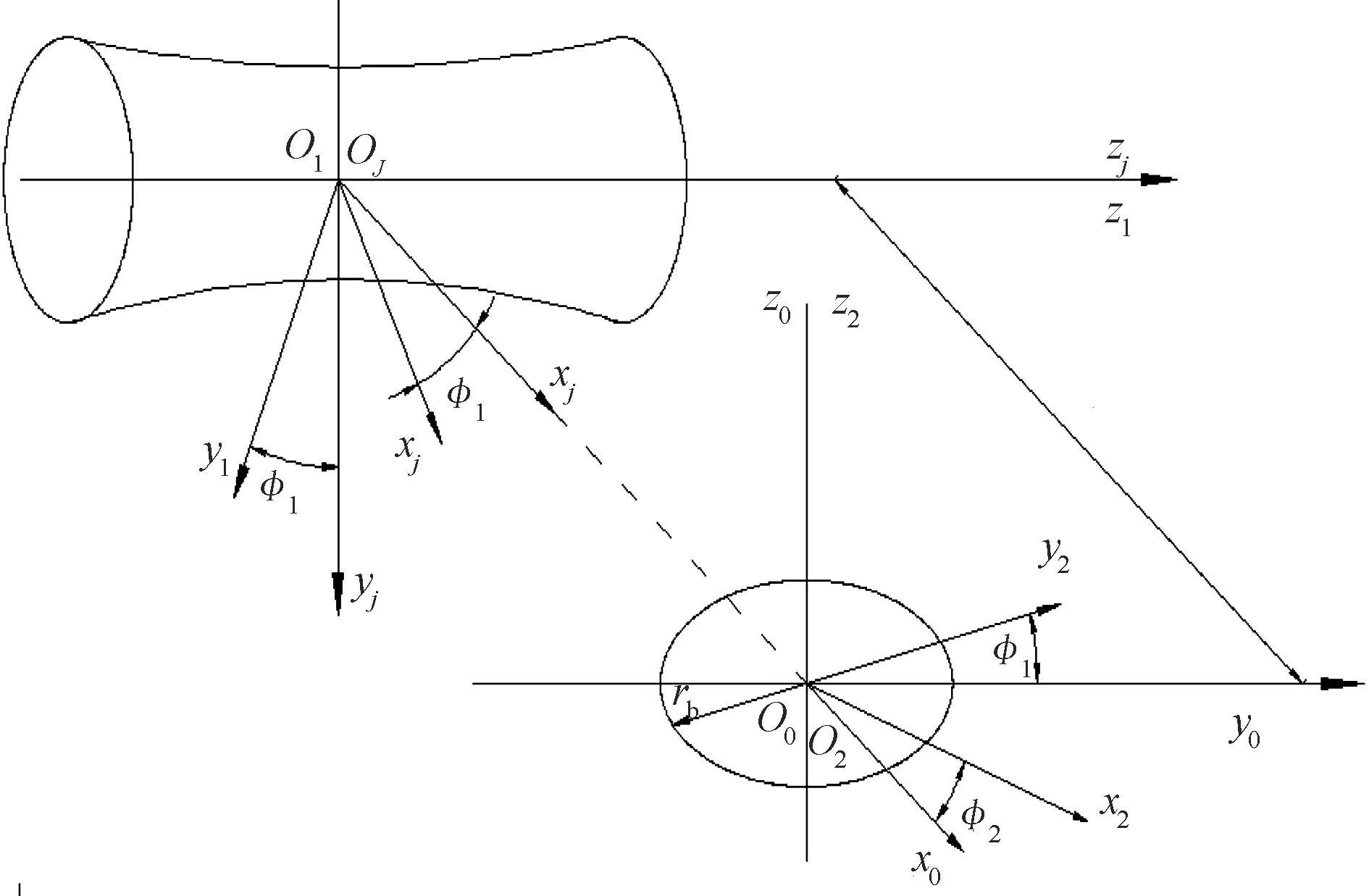
图1 包络坐标系的建立

利用空间啮合原理和旋转变换矩阵法可推导出蜗杆理论廓面方程为:

(1)

由蜗杆齿面方程[1]可知，式(1)为关于u和φ2(φ1)的函数，且其齿面接触线为直线。φ2、φ1分别为第2次和第1次包络转角。当确定某一φ2(φ1)值时，即得到某一时刻蜗杆齿面上的一条接触线，此时变换u值即可得此接触线上沿齿高方向的不同点。φ2和u值范围可由以下几何关系[5]求得：

(2)

式中：φi为蜗杆工作起始角；φh为蜗杆工作半角；rf2、ra2分别为与蜗杆配对的蜗轮的齿根圆弧半径和齿顶圆弧半径。

构造蜗杆齿面时，首先将工作角φ2以一定的步长进行离散，然后在每一确定的φ2处取u的最大值和最小值分别代入蜗杆齿面方程式即可得到接触线两端点，最后将所有点拟合即可得蜗杆齿面。

2 机床几何空间误差建模理论

本节详细介绍蜗杆加工数控机床的结构、低序阵列图以及低序体阵列表。下面根据机床结构给出各轴运动误差。图2中四轴加工机床在实际加工中每根运动轴将包含6项运动误差：TMX、TMY、TMZ、RMX、RMY、RMZ。其中，RMX、RMY、RMZ是转动误差，TMX、TMY、TMZ是移动误差。机床在加工工件过程中所有的误差都是在变化的，所以移动量与转动量也是变化的；因此，机床就产生了24(4×6)项运动误差。同时，主轴产生3项热漂移误差，X、Y、A、B轴又会产生4项垂直误差，分别是Sxz、Sax、Say、Syx、Sab，一共37项误差。T、R、S分别表示移动误差、转动误差、垂直度误差[6]。求出的各特征矩阵如下。

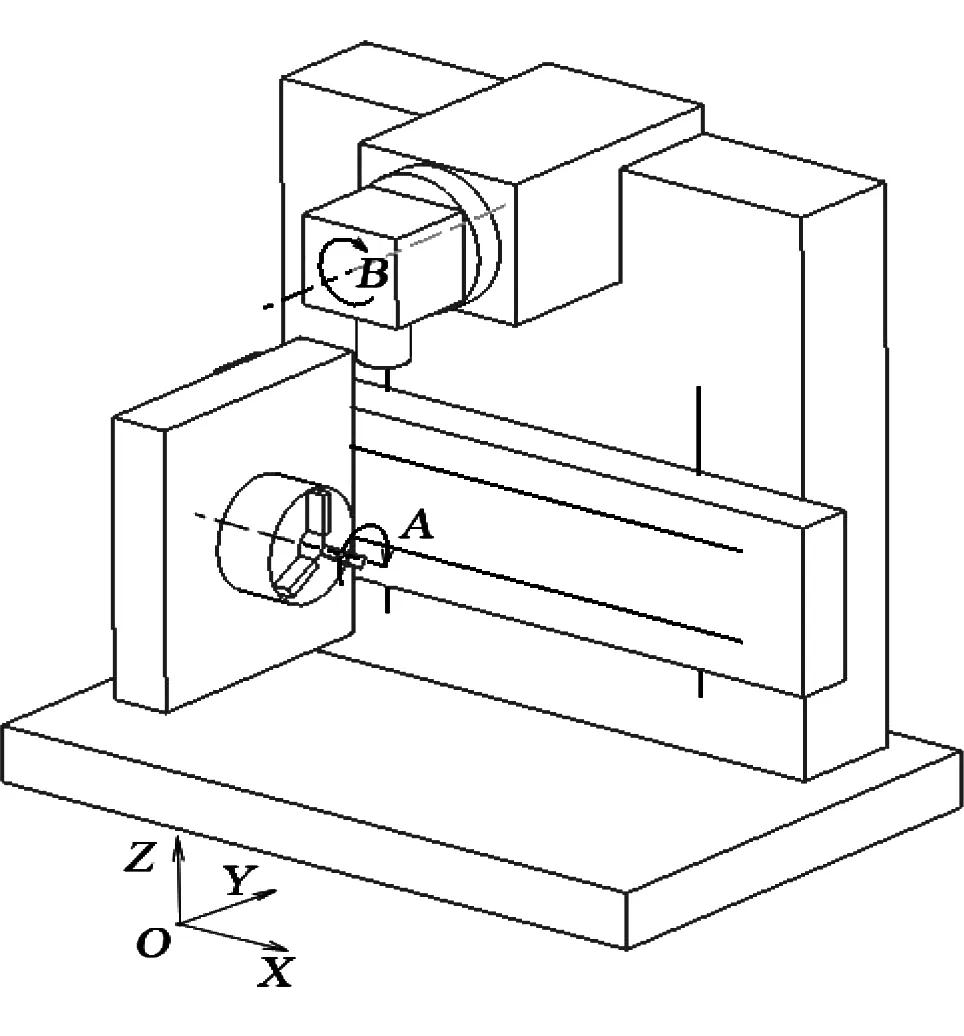
图2 蜗杆加工机床示意图

1)主轴与Y轴的转换矩阵

(3)

2)Y轴的转动变换矩阵

VXY=[VXY]pe[VXY]s[VXY]se=

(4)

其中，Y为其角位移。

3)X轴的移动变换矩阵

VZX=[VZX]pe[VZX]s[VZX]se=

(5)

其中，X为其角位移。

4)Z轴的移动变换矩阵

VOZ=[VOZ]s[VOZ]se=

(6)

其中，Z为其移动位移。

5)A轴的转动变换矩阵

VOA=[VZX]pe[VZX]s[VZX]se=

(7)

其中，A表示其角位移。

6)B轴的转动变换矩阵

VTB=[VTB]pe[VTB]s[VTB]se=

(8)

其中，B表示其角位移。

设刀尖点在刀具坐标系的位置矢量t=[0 0 0]T，理论切削点在工件坐标系中的位置矢量w=[xWyWzW]T，那么刀尖点和理论切削点在机床床身坐标系中的位置矢量tO、wO分别为：

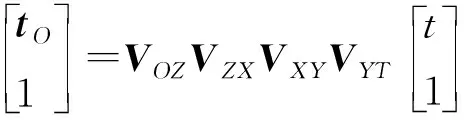
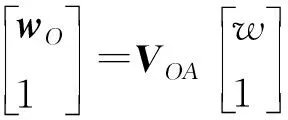
(9)

式中：VOZVZXVXYVYT表示从刀具到床身的刀具分支坐标变换矩阵；VOA表示从工件到床身的工件分支坐标变换矩阵。

令e=[ΔxΔyΔz]T表示机床加工的误差矢量，则有

(10)

用牛顿迭代法[5]求解和φc的值，将其代入理论工作廓面方程即可得蜗杆理论廓面上点P2的坐标(x,y,z)。平面二次包络环面蜗杆廓面的法向误差为

(11)

式中：P1是误差点；P2是蜗杆理论廓面上的点。

将式(3)—(10)的变换矩阵带入式(11)，计算得机床加工蜗杆廓面误差

Re=R·VOZVZXVXYVYTVTB-C

(12)

式中C为蜗杆毛坯的转动中心在第1次包络坐标系的位矢量。

3 计算结果与实例分析

3.1 蜗杆法向误差计算

本文以一蜗杆计算为例进行分析。蜗杆的具体参数：中心距a=200 mm，基圆半径rb=65 mm，蜗杆分度圆直径d1=70 mm，母平面倾角β=10°35′,蜗杆头数=1，传动比i=40，蜗杆工作起始角φi=7°14′,蜗杆工作半角φh=15°5′，rf2=157.575 mm,ra2=170.775 mm。

由式(1)、(2)可得φ2、u的范围分别是：7°14′≤φ2≤39°10′；143.544 mm≤u≤157.920 mm。误差计算时蜗杆坐标系X2=h的步长取为1 mm，S2动坐标系转角φ2的步长取为4°进行计算。

设各轴误差偏移量为1×10-3mm，角误差转动量为0.5×10-6rad，误差数据如图3—8。

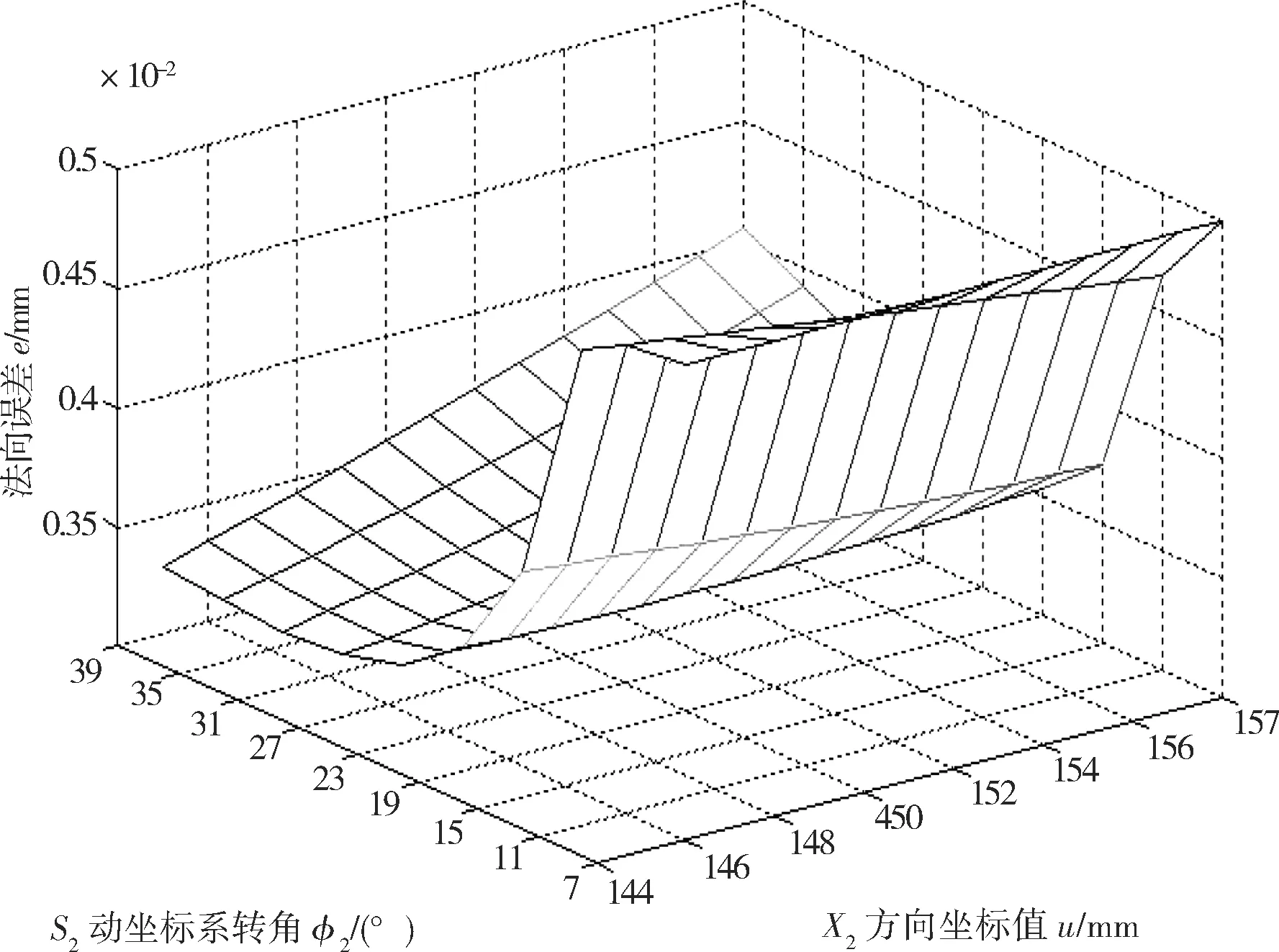
图3 X轴误差对法向误差的影响

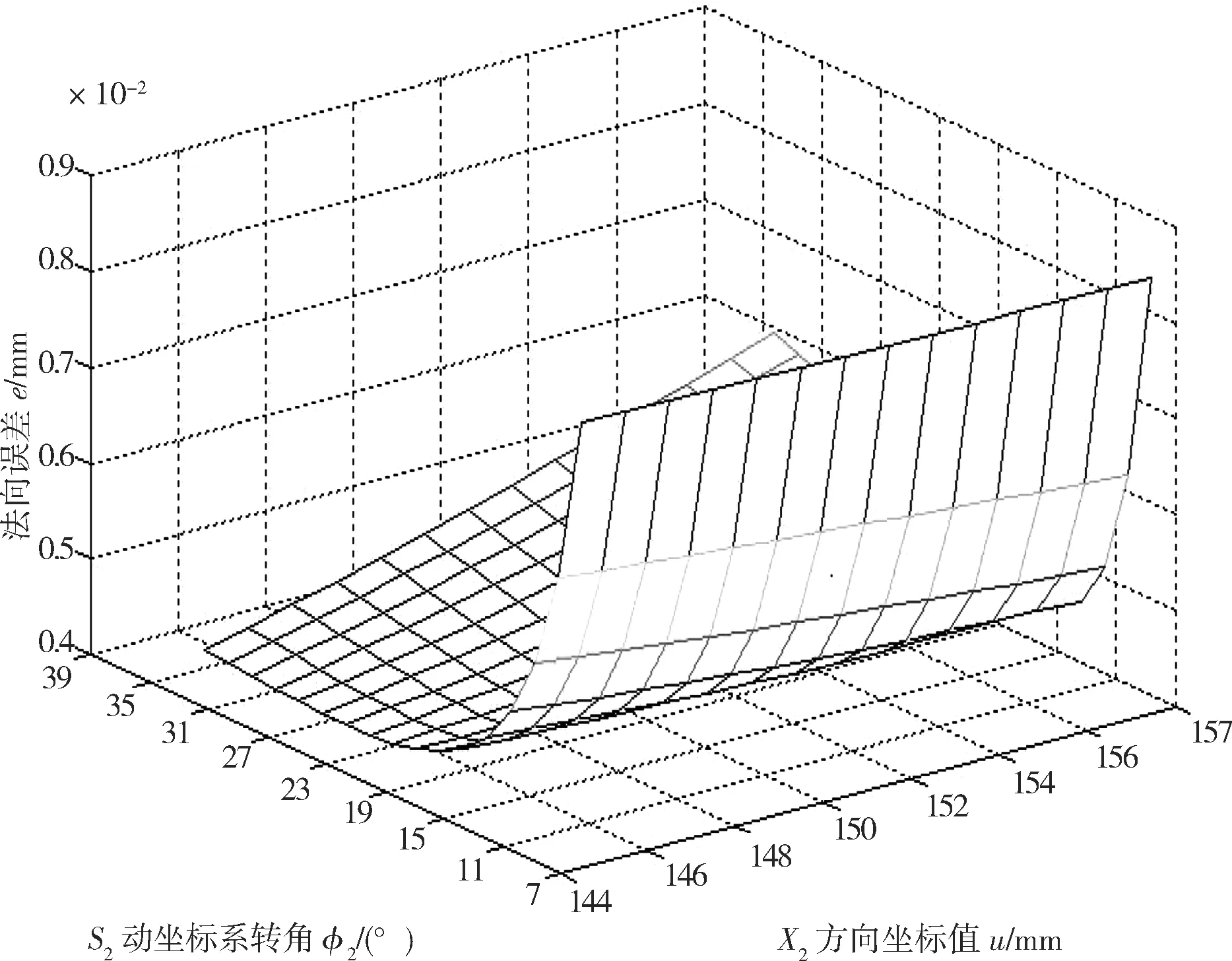
图4 Y轴误差对法向误差的影响

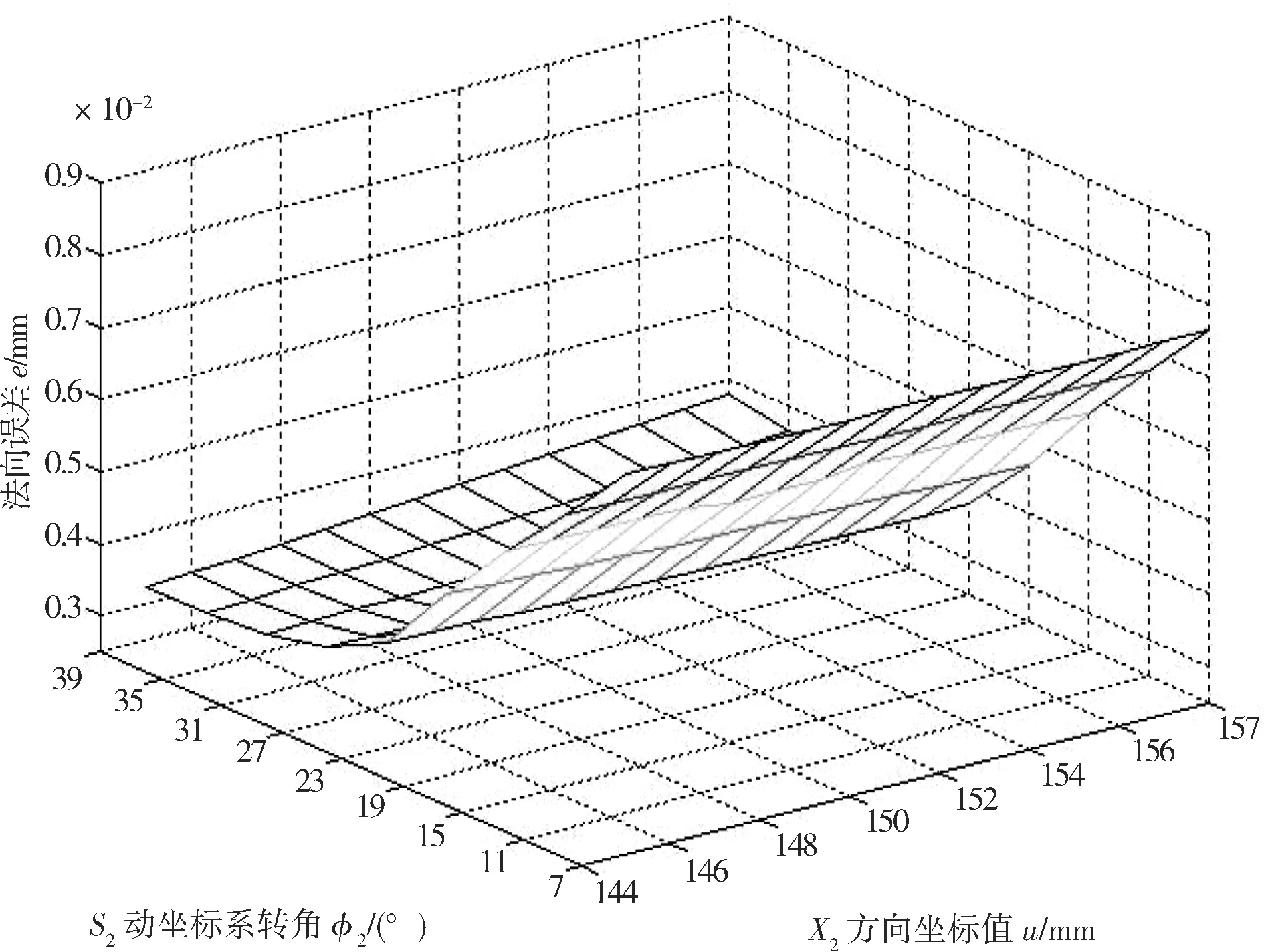
图5 Z轴误差对法向误差的影响

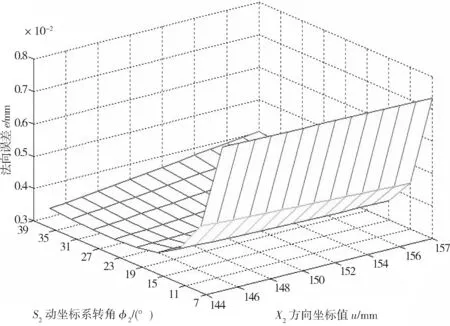
图6 A轴误差对法向误差的影响

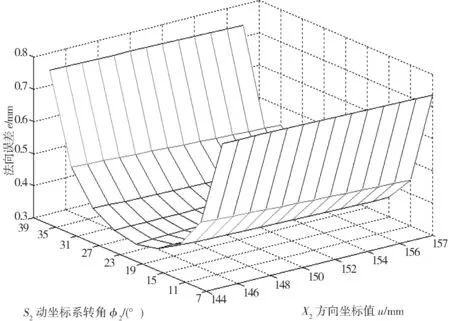
图7 综合误差对法向误差的影响

3.2 结果分析

如图3—8所示，在蜗杆副数控机床切削加工中，根据输出的蜗杆副误差输出数据，取机床原始误差对蜗杆法向误差的影响平均值进行排序，从大到小为Z轴、主轴、A轴、X轴。

X轴对法向误差的影响在7°～23°区间递减，在23°～39°区间上升，沿着u方向误差增加，如图3所示。Y轴对法向误差的影响在7°～19°区间递减，在19°～39°区间沿着u方向增加0.002 mm，如图4所示。Z轴对法向误差的影响在7°～23°区间线性递减，在23°～39°区间变化不大，且沿u坐标方向误差很小，可以认为u对Z轴的误差几乎没影响，如图5所示。A轴对法向误差的影响在7°～19°区间递减，在23°～39°区间变化不大，且沿u方向的误差递增，Δe≤0.001 mm。综合误差对法向误差的影响在7°～23°区间递减，在23°～39°区间递增呈U型分布，在23°取得最小，e=0.003 mm。

4 结论

1)引入数控机床各轴运动误差到平面二次包络环面蜗杆廓面误差分析中，推导出包含机床各轴运动误差的平面二次包络环面蜗杆误差廓面方程，给出了平面二次包络环面蜗杆廓面法向误差的计算方法。

2)通过实例计算分析，其结果表明，机床综合误差对平面二次包络环面蜗杆廓面精度影响较大，所以在平面二次包络环面蜗杆实际加工过程中必须严格控制这些综合误差。

3)本文的研究成果对于数控机床各轴运动误差补偿和平面二次包络环面蜗杆廓面精度的预测以及高精度平面二次包络环面蜗杆的制造提供了理论参考。

[1]周良墉. 环面蜗杆的曲率修形原理[J]. 机械工程学报, 2002， 38(2): 112-115.

[2]Chen K， Tsay C. Mathematical Model and Worm Wheel Tooth Working Surfaces of the ZN-type Hourglass Worm Gear Set[J]. Mechanism and Machine Theory, 2009,44(9): 1701-1712.

[3]任永强，杨建国，窦小龙，等. 五轴数控机床综合误差建模分析[J]. 上海交通大学学报：自然科学版, 2003,37(1): 70-75.

[4]夏江敬, 胡剑,张仲甫，等.平面二次包络环面蜗轮副三维建模与数控仿真[J]. 武汉理工大学学报:信息与管理工程版, 2003，25(1): 81-83.

[5]黄安贻，夏江敬，张仲甫，等. 平面包络环面蜗杆啮合齿面的结构特性及其应用[J]. 武汉理工大学学报:信息与管理工程版, 2003，25(1):67-70.

[6]粟时平，李圣怡. 多体系统理论在数控加工精度软件预测中的应用[J]. 组合机床与自动化加工技术, 2004 (3) :28-32.

[7]单乐生，徐燕申，陈永亮，等. 基于CAD平台及其开发工具的箱体类零件CAD/CAPP集成系统开发技术[J]. 制造业自动化, 1999 (5) :15-18.

[8]Zhao Y D, Su Z Zhang. Meshing Analysis and Technological Parameters Selection of Dual Tori Double-enveloping Toroidal Worm Drive[J]. Mechanism and Machine Theory, 2010, 45(9): 1269-1285.

[9]Oiwa T K , Kobayashi A Toyama. Grinding of Highly Accurate Hourglass Worm Gears: Trial Manufacture of the Worm Grinding Device[J]. Precision Engineering, 1990, 12(2): 85-90.

[10]段振云，金嘉琦，郑鹏，等. 齿轮整体误差测量过程的平差效应[J]. 机械工程学报, 2001，37 (2) :55-57.