细长轴的车削仿真研究
2014-09-04
(西华大学机械工程与自动化学院,四川 成都 610039)
细长轴类零件在加工过程中容易产生弯曲变形,改变了刀具的实际切削路径,降低了零件的机械加工精度, 使其很难获得理想的加工尺寸[1]。它的加工一直被认为是机械加工中的工艺难题。目前研究提高细长轴类零件加工精度的方法主要有:1)改变装夹方式,将传统的一夹一顶的方式改进为两顶尖装夹方式;2)改变切削力的进给方向,将正向切削加工改进成逆向车削加工。本文在对传统的单刀车削加工方法的力学建模和受力分析的基础上,提出对称式双刀车削的加工方法,并建立双刀车削力学模型分析其受力情况,以论证双刀车削加工方法的可行性。通过ANSYS有限元法[2]对2种车削加工精度的仿真结果表明,双刀车削方法能够提高轴类零件的加工精度。
1 细长轴的弯曲变形分析
1.1 单刀切削的弯曲变形模型
细长轴在机械加工时,由于沿着轴方向的进给力Fx对工件产生的弯曲变形可以忽略不计,因此细长轴类零件加工产生的弯曲变形主要来自刀具在y轴和z轴方向的作用力Fy、Fz。切削力Fy、Fz改变了刀具在切削加工中的实际背吃刀量,影响了工件加工的最终成形尺寸,从而产生了加工误差。
在受力分析中,把卡盘夹紧端A简化成固定端,限制全部自由度。回转顶尖的一端B简化为铰支座,限定z轴方向的自由度,如图1所示,受力模型为径向力Fz使工件在z方向上产生弯曲变形[3-7]。

图1 细长轴在径向力作用下的力学模型
如图1所示坐标,由静力平衡方程可得:
∑FZ=FB+FA-F=0
(1)
∑MA=MA-Fa+FBl=0
(2)
2个方程要求解3个未知量,必须补充1个形变方程。利用奇异函数法写出细长轴的挠曲线方程。在奇异函数中定义:若x
EIw″=FA
(3)
对式(3)进行积分得
(4)
根据边界条件x=0时w′=0求解,得C1=0。对式(4)再进行积分得
(5)
根据边界条件x=0时w=0求解,得C2=0;再把边界条件x=l处w=0代入 式(5),得
(6)
通过联解方程组(1)(2)(6)求解,得:
所以挠曲线微分方程
(7)
1.2 双刀切削的力学模型
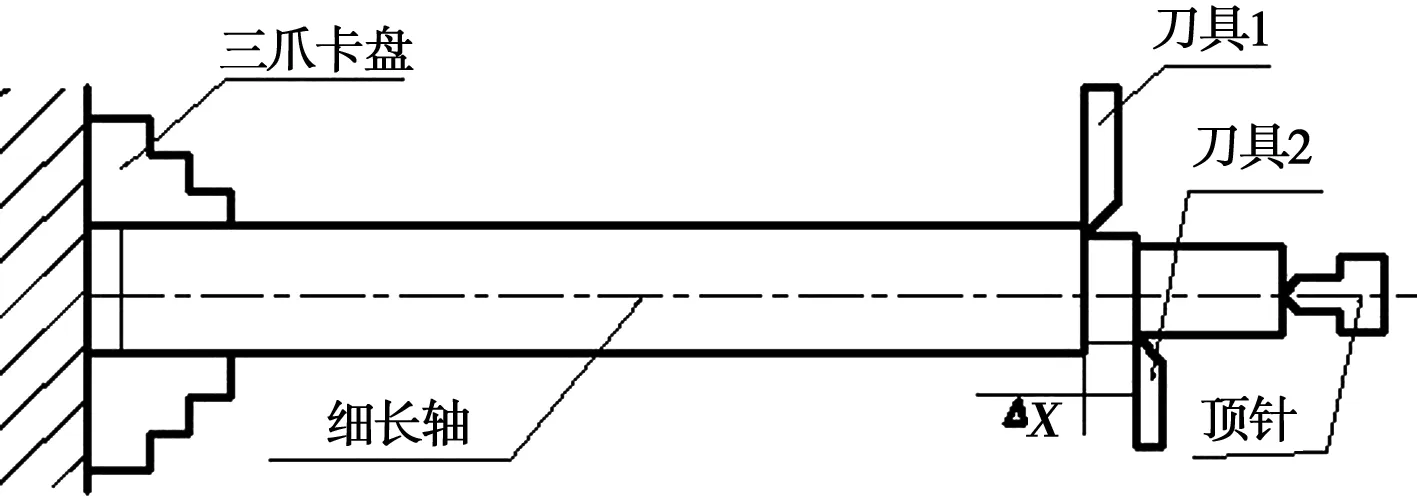
图2对称式双刀车削结构示意图
2把刀具分布在轴的两侧,轴向间距为Δx,Δx为一恒定而且微小的值。刀具1先对工件加工,刀具2再对工件进行第2次加工,这样就把原来的1次加工分成了2次加工,减小了双刀车削中单把刀具的切削力。设计2把刀具在轴上如此分布的目的是使其产生的弯曲变形可以相互抵消,以减小细长轴在纵向方向的弯曲变形量。
1.3 双刀车削力学模型分析
根据双刀车削中一夹一顶的装夹方式,结合加工的实际情况,在受力分析时把卡盘夹紧端简化成固定端A,限制全部自由度,回转顶针的一端简化为铰支座B,限定z轴方向的自由度,这样就把它简化成一个超静定梁的问题。
图3是双刀车削中细长轴在zox平面的受力分析模型。F1、F2表示刀具径向力,当2把刀具的背吃刀量相等时,即ap1=ap2,根据刀具切削力经验公式[8]可知,在双刀车削方案中,工件材料、刀具几何参数、进给量、切削速度相同,刀具的切削力由刀具背吃刀量ap决定。由于在一般切削力实验公式中,背吃刀量ap的指数xFZ接近于1,背吃刀量ap与刀具切削力F近似成正比,因此F1=F2。由于它们的横向间距Δx相对l来说很微小,所以可以把作用在细长轴的刀具径向力F1、F2等效于一个力偶MF,力偶MF与A端距离为a+Δx/2,与B端距离为b+Δx/2,这里采用奇异函数法求解。
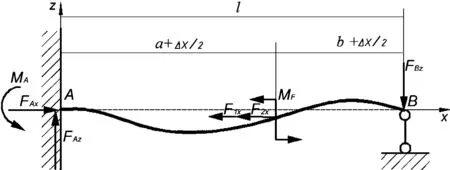
图3 对称式双刀车削力学模型
根据静力平衡方程
∑FZ=F1+FBz-F2-FAz=0
得
FBz=FAz
(8)
由静力平衡条件可知
∑MA=MA+MF-FBzl±FAxw合=0
即
MA+MF-FAzl±FAxw合=0
(9)
其中±表示与w合同号,MF=ΔxF1。
根据静力平衡方程
∑Fx=F1x+Fx-FAx=0
得
FAz=F1x+F2x
式(9)中还剩下MA、FAz是未知量,要求解必须还要增加一个基于体系形变的方程,因此利用奇异函数法写出细长轴的挠曲线方程
(10)
利用边界条件x=0,w=0,w′=0 和x=l,w=0,求解,可得到细长轴的挠曲线方程。
如果分离出刀具进给力,只研究刀具径向力使细长轴产生的弯曲变形,那么令式(9)、(10)中的FAxw合因子为0,对式(10)两边求积分
(11)
根据边界条件x=0时w′=0求解,得C1=0,对式(11)两边再进行一次积分得

(12)
根据边界条件x=0时w=0求解,得C2=0。再把边界条件x=l处w=0代入式(12)得
(13)
联立式(9)(13)2个方程组可求得:
最后求解出双刀车削中细长轴在径向力作用下的变形挠曲线微分方程为
(14)
2 双刀车削有限元模型
双刀车削模型是以梁理论为基础建立的简支梁模型,把卡盘处简化为固定支撑,回转顶尖处简化为铰支座,细长轴全长为l。采用有限元方法把细长轴离散为100个节点进行分析,节点编号如图4所示,节点1处为固定端,节点2处为铰支座,径向力F1、F2分别作用在节点71、72处,双刀车削仿真模型如图4所示。
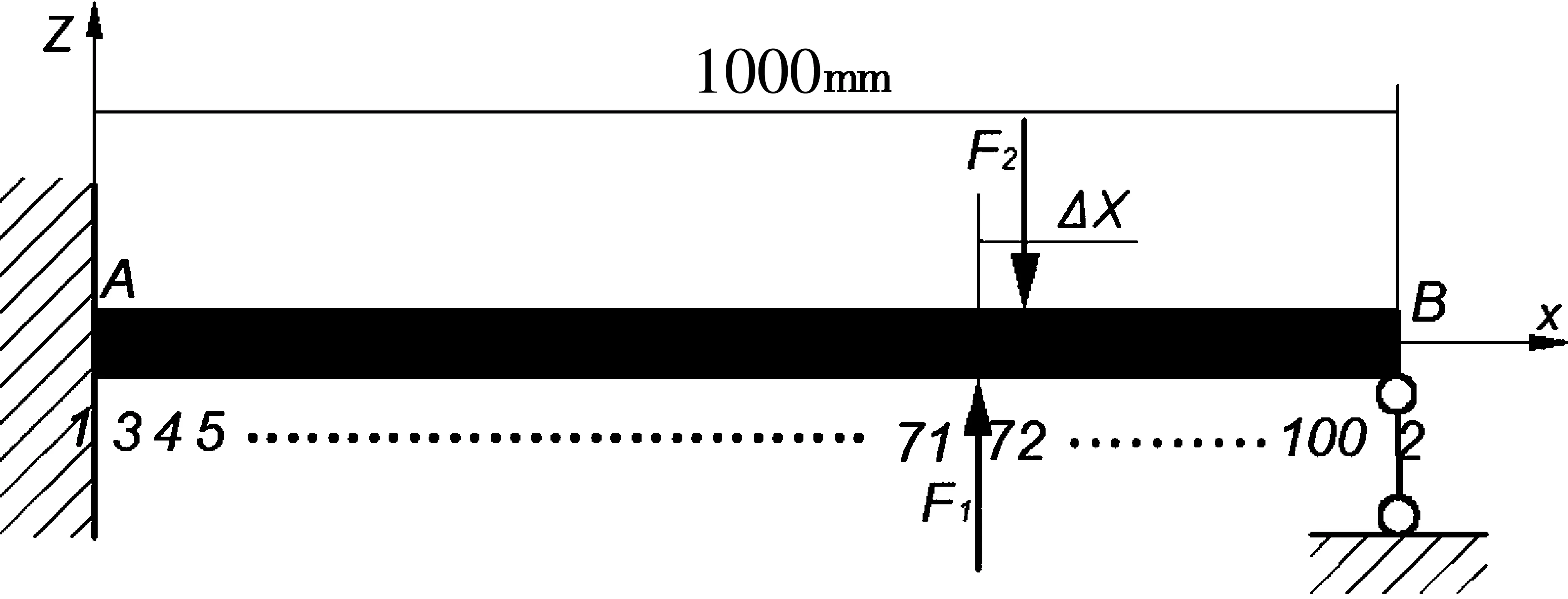
图4 对称式双刀车削仿真模型
3 有限元仿真分析
已知条件:细长轴长为1000 mm,直径为50 mm,材料为45号钢,密度为7.8 g/cm3,泊松比为0.3,重力加速度为9.8 N/kg ,转速为600 rad/s,进给速度为0.5 mm/r,E=210 GPa。本次仿真加工中普通车削加工背吃刀量设置为2.0 mm;双刀车削加工中第1组刀具1背吃刀量设置为1.5 mm,刀具2背吃刀量设置为0.5 mm,第2组刀具1背吃刀量设置为1 mm,刀具2背吃刀量设置为1 mm;双刀车削设置为在71号节点z轴方向施加107 N的作用力F1,在72号节点z轴方向施加-38.4 N的作用力F2,普通车削设置为在71号节点z轴方向施加132 N的作用力F。该仿真选取Beam188单元作为分析单元,按实验所需,在细长轴x方向上进行网格划分,分成100份,然后进行求解。
图5示出一般普通车床加工细长轴零件受力后的变形情况:最大变形位置在轴的l/2附近处 ,最大位移量为18.4 μm,位移方向向上。图6示出第1组双刀车削加工细长轴零件受力后的变形情况:最大变形位置也在轴的l/2附近处 ,最大位移量为9.84 μm,位移方向向上。图7示出第2组双刀车削加工细长轴零件受力后变形情况:最大变形位置也在轴的l/2附近处 ,最大位移量为0.446 μm ,位移方向向上。加工相同背吃刀量细长轴时,双刀车削方案引起的最大挠度比普通车削引起的最大挠度小。 可见,双刀车削方案能较明显地提高细长轴车削的加工精度。
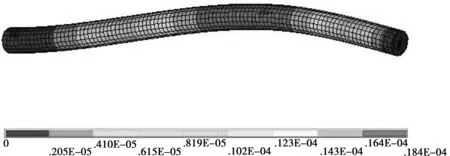
图5 经普通车床加工后零件变形图

图6 经双刀车削法加工后零件变图(第1组)
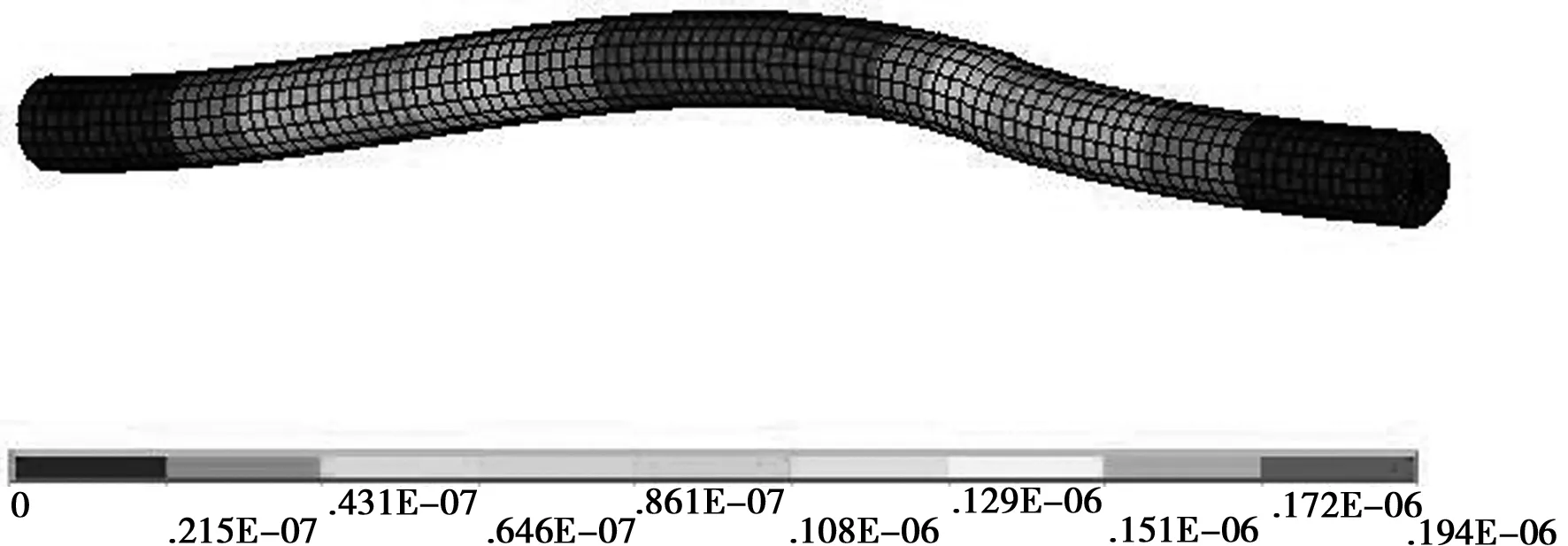
图7 经双刀车削法加工后零件变图(第2组)
4 结论
仿真结果表明,对称式双刀车削加工细长轴的方法能满足零件加工精度要求。通过改变刀具切削力在细长轴上的分布情况,能有效地解决细长轴因受刀具切削力引起的弯曲变形的问题,能提高零件的加工表面质量和几何形状精度。
[1] 吴能章.轴类零件加工的鼓形误差预报与补偿[J].西华大学学报:自然科学版,2005,24(1):41-44.
[2] 李娅,赵文.有限元网格自动剖分及优化方法[J].西华大学学报:自然科学版,2003,22(3):106-108.
[3] 戴海港,邓志平.细长轴的双刀车削加工方法[J].组合机床与自动化加工技术.2010(6):88-89.
[4] 赵刚,邓志平,陈胜金.精密细长轴数控车削自适应加工研究[J].煤矿机械.2013,34(1):133-135.
[5] 李健,庞勇.细长轴车削加工径向变形和切削力的分析计算[J]. 组合机床与自动化加工技术,2012(2):23-25.
[6]杨红义,李卫民,潘静,等.基于ANSYS的细长轴车削过程中的模态分析[J].辽宁工业大学学报,2008,28(4):242-245.
[7]郭建亮,崔伯第,郑书华,等.基于切削力测量的细长轴加工误差在线补偿[J].机床与液压,2009,37(12):66-67.
[8] 邓志平.机械制造技术基础[M].成都:西南交通大学出版社,2008:82-84.
