基于时变Copula GARCH模型的金融风险度量

刘 娟1,， 王 沁，刘 曦 ，昌春艳

(1.湖南科技学院数学与计算科学系计算数学研究所，湖南 永州 425199；2.西南交通大学数学学院，四川 成都 610031)

Copula目前在金融领域的应用非常广泛，特别是在金融市场上的风险管理、投资组合的选择、资产定价等方面。利用Copula函数，可以将若干个随机变量的边缘分布连接为联合分布[1]。Copula函数的引入，可将金融资产的风险分解成单个资产的风险和投资组合产生的风险2部分，其中单个资产的风险可以由各自的边缘分布来描述，而投资组合产生的风险则由他们的连接函数来刻画。Copula建模的方法与普通的线性相关的建模方法不同，且其导出的相依指标在单调变化下具有不变性[2-3]。时变Copula即变量之间相关系数的时变，最先提出时变相关Copula模型的是Patton[4],用一个类似ARMA(1,10)的过程来描述二元正态Copula函数的相关参数。Van den Goorbergh等[5]将动态Copula模型应用于2种不同的金融市场，并对其结果作对比分析。B. Candelon等[6]运用时变Copula模型对金融危机后的股票市场进行分析。龚朴等[7]建立了用于描述时变相依参数的新的演化方程，采用时变条件t-Copula模型对我国人民币汇率制度改革前后美元、欧元和日元兑人民币汇率之间的相关性进行了研究。杨楠等[8]通过构建效用评估函数，使用时变相关t-Copula模型、蒙特卡洛模拟和VaR计算方法系统研究了我国国际储备的最优结构。

本文采用Kendall tau 来构建其相关系数的时变性，从而达到时变Copula的目的。本文内容安排如下：第1部分时变相关Copula理论；第2部分针对金发科技和ST国农2支股票数据建立Copula模型；第3部分利用所建立的Copula模型计算VAR；第4部分是小结。

1 时变相关Copula

1.1 秩相关参数

时变相关Copula模型的关键在于Copula函数的相关参数的时变形式。Copula函数的相关参数常见的有Kendall tau 、spearman rho 、尾相关。 Kendall tau 、spearman rho是一个全局变量，而尾相关是一个局部变量，本文选取Kendall tau 作为Copula函数的相关参数。下面介绍Kendall tau[9]。

定义1设X=(x1，x2)，Y=(y1，y2)，且(x1,y1)、(x2,y2)是独立同分布的随机向量，令Kendall tau秩相关系数τ为

τ=P[(x2-x1)(y2-y1)>0]-P[(x2-

x1)(y2-y1)<0]=2P[(x2-x1)(y2-y1)>0]-1

(1)

若随机变量X、Y的边缘分布分别为F(x)、G(y),相应的Copula函数为C(u、v)，其中u=F(x),v=G(y)，u,v∈I,I=[0,1]，则Kendall tau秩相关系数τ为

τ=4∬I2C(u,v)dC(u,v)-1

(2)

1.2 Copula函数及边缘分布函数的选取

由于金融时间序列的分布多呈现时变、波动集群、高峰等特性，本文选取Copula函数为二元正态Copula函数，对应的边缘分布为GARCH模型。

二元正态Copula函数的分布函数及其密度函数的表达式分别为：

(3)

(4)

其中：Φ-1(·)是标准一元正态分布函数Φ(·)的逆函数；ρ为相关参数，即为Φ-1(u)与Φ-1(t)的线性相关系数；u、t为边缘分布数据。

Bollerslev给出的GARCH(p,q)模型[10]为：

(7)

其中εt是随机扰动项，且E(εt)=0。

2 Copula模型的建立

2.1 数据的选取及其描述性统计

本文选取ST国农和金发科技2支股票的日收盘价，数据选取2011年1月4日到2012年5月31日之间的数据，数据来自CCER数据库。P为收盘价，收益率：Rt=lnpt-lnpt-1,由此得到金发科技和ST国农的日收益率数据。在组合中，金发科技和ST国农的权重比分别为1∶1和3∶7。表1为各收益率序列的总体指标，表2为指数收益率序列的单位根检验值。2种股票的日收益率线图如图1所示。

表1 ST国农和金发科技的描述性统计

图1 2种股票的日收益率线图

由表1和图1可以看出，2只股票有一定的丛集性，存在尖峰的现象。ST国农数据较金发科技数据平稳。

表2 金发科技与ST国农的单位根检验

ADF检验的原假设是2支股票均存在单位根，由表2可以看出，其P值趋于0，所以拒绝原假设，2支股票不存在单位根，数据是平稳的时间序列。

2.2 GARCH模型的建立

根据前面的描述性统计，本文对其边缘分布建立GARCH(1,1)-Norm模型，得到其参数估计如表3所示。

表3 GARCH(1,1)-Norm模型的参数估计

观察表3，2只股票其α+β项的值均小于1，故可知其GARCH(1,1)模型是平稳的，95%的置信水平下其参数估计是显著的。所建立的GARCH(1,1)模型分别为：

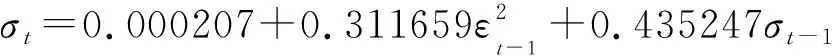
2.3 时变Copula

根据Kendall tau的定义，本文采用滑动窗宽的方法来构建时变Kendall tau,其具体步骤如下：

1)对金发科技与ST国农所建立的GARCH模型中的et1,et2作概率积分变换，得到的数据分别用u,t表示。

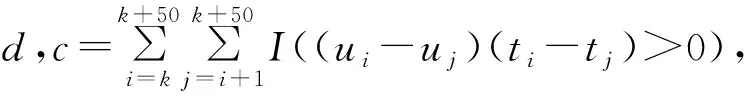
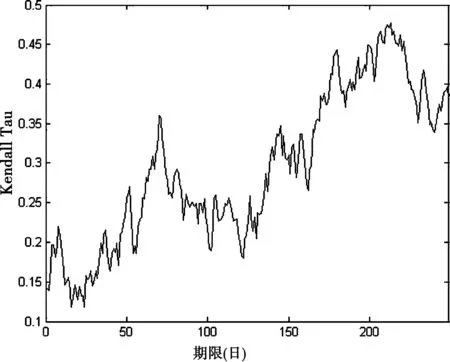
图2 滑动窗口为50的Kendall tau 线图

Kendall tau是一个全局变量，它反映了变量之间相关系数随时间发生的变化。

总体参数ρ与Kendall tau存在如下的一一对应关系

(8)

根据ρ与Kendall tau存在的一一对应关系得到ρ的时变图(见图3)。

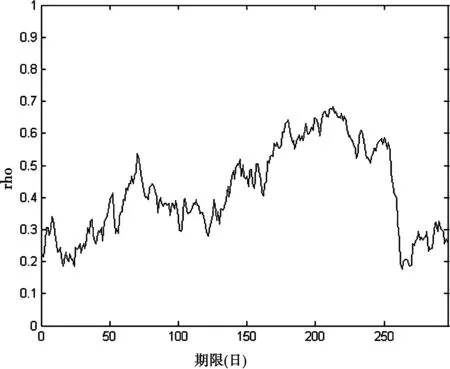
图3 总体参数ρ的时变图

3 蒙特卡洛模拟计算VaR

建立了恰当的时变正态Copula模型的前提下，采用蒙特卡洛模拟方法计算资产组合风险值的程序如下：

Step1: 利用时变参数ρt产生100个随机数对(μ1,μ2)～CGaussian(.,.)，取第50个数对为(μt1,μt2)。

Step3:用所建立的GARCH(1,1)模型，计算

(9)

Rt1=0.5xt1+0.5xt2

(10)

Rt2=0.3xt1+0.7xt2

(11)

其中：Rt1为金发科技和ST国农的比例为1∶1的组合：Rt2为金发科技和ST国农的比例为3∶7的组合。

Step4: 将所得的Rt1、Rt2按从小到大的顺序排序，取对应分位数下的值即为所求VaR。

本文对VaR的准确性检验采用的是Kupic等的失败检验法[11]。该方法假定VaR估计具有时间的独立性，实际损失超过VaR的估计为失败，实际损失低于VaR为成功。假定计算VaR的置信度为C，实际考察天数为T，失败天数为N，则失败率为p(N/T)。GARCH(1,1)-Norm下的VaR如表4所示。

表4 GARCH(1,1)-Norm下的VaR

由表4可以得出，ST国农在置信水平为95%时，其风险要比金发科技的好，但是在置信水平为99%时，其风险要比金发科技大。无论置信水平是在95%或者是99%，其组合资产风险均要小于单个资产的风险，这跟实际情况是相符的，当组合权重分别为0.5和0.5时其风险要比其组合权重为0.3和0.7的低，不同权重的资产组合其风险不同。

4 结论

本文选取ST国农和金发科技2支股票的日收盘价，取其对数收益率，对每只股票的数据建立GARCH(1,1)-Norm模型，根据GARCH(1,1)-Norm模型的残差项建立时变Kendall tau,由时变Kendall tau 模拟产生服从二元正态Copula的随机数据，最终根据其产生的随机数据，利用蒙特卡罗模拟技术计算其单个资产风险和组合资产风险，得出组合投资能减低风险的结论。

同时由表4可以看出不同权重的资产组合其风险不同，本文只是列举2种不同的权重，而如何找到不同股票数据的最佳权重，有待进一步研究。

[1]刘伟,陈功,马利军.含状态转换的Copula模型及其应用[J].运筹与管理，2009,18(5):120-125.

[2]高岳,王家华,杨爱军.具有时变自由度的t-Copula蒙特卡罗组合收益风险研究[J].中国管理科学，2011,19(2):10-15.

[3]韦艳华，张世英.金融市场的相关性分析：Copula-GARCH模型及其应用[J].系统工程，2004,22(4):7-12.

[4]Patton A J.Modeling Time-varying Exchange Rate Dependence Using the Conditional Copula[D]. San Diego :University of Califonia,2001.

[5]Van den Goorbergh R W J, Genest C, Werker B J M. Bivariate Option Pricing Using Dynamic Copula Models[J]. Insurance: Mathematics and Economics, 2005,37:101-114.

[6]Candelon B，Manner H. Testing for Asset Market Linkages: A New Approach Based on Time-varying Copulas[J]. Pacific Economic Review, 2010,15:364-384.

[7]龚朴,黄荣兵.外汇资产的时变相关性分析[J]. 系统工程理论与实践, 2008(8):26-37.

[8] 杨楠,邱丽颖.我国国际储备资产的最优结构研究：基于时变Copula及VaR的投资组合模型分析[J]. 财经研究, 2012,38(5):15-27.

[9] Nelsen R B.An Introduction to Copulas[M]. New York:Elsevier Science,2006:158-160.

[10]Botterstev T. Generalized Autoregressive Conditionat Heter os Kedastility[J]. Jourhat of Econometrics，1986，31:307-327.

[11] Kupic,Paul. Techniques for Verifying the Accuracy of Risk Measurement Model.Journal of York[J].Journal of Derivatives,1995:73-84.