基于蚁群算法的公共自行车系统调度算法研究
2014-09-04,2,3,2,3
,2,3,2,3
(1.西南交通大学交通运输与物流学院,四川 成都 610031;2.综合运输四川省重点实验室,四川 成都 610031;3. 交通运输智能化国家地方联合工程实验室,四川 成都610031)
公共自行车系统是一种创新型自行车交通模式[1]。其目的是通过将自行车与其他几种交通方式结合,使之成为城市公共交通的一部分,成为居民交通出行的重要选择。公共自行车系统的实施不仅可以降低出行成本、提高道路资源利用效率、缓解交通拥堵,还能节能减排,提高城市的空气质量。
围绕公共自行车,学者们进行了大量的研究[2-14]。这些研究成果为公共自行车系统的实施与发展提供了有力的支撑,但是它们大多是对系统运营和租赁点位置确定的研究,对于不同租赁点之间公共自行车车辆调配路径选择没有进行深入阐述和量化分析。文献[15]虽然运用蚁群算法得到公共自行车最优调度回路,但是没有考虑1d内不同时段公共自行车的借还需求情况。为得到符合实际需求的调配路径方案,本文在考虑不同时段车辆借还特点条件下建立路径优化模型。
1 公共自行车调配路径优化模型
确定车辆调配的路径,需分别考虑平峰时期租赁点自行车数量均衡和高峰时期租赁点租赁需求被拒绝率低的调配目标。在平峰时的车辆调配或早晚高峰前的预调配时,由于租赁点借还量较小,可以不考虑租赁点的自行车数量随时间变化而变化,因此不考虑时间约束。在高峰期调配过程中,租赁点借还量大,借还速率快,租赁点的自行车数量随时间变化而变化,租赁点在还未被调配之前可能就出现无车可借或者无停车桩可还车的情况,这时需求者借还车要求将会被拒绝,因此高峰期车辆调配路径优化模型需要考虑时间因素。为此,建立以上2种模型,并作以下假设。
1)用有向图G=(A,E)表示公共自行车车辆调配网络。A={0,1,2,…,n}表示租赁点的集合,0点表示调度中心;E={(i,j)|i,j∈A,i≠j}表示相连租赁点的边集;V={0,1,2,…,m}表示调度车的集合。
2)调度车均从调度中心出发,并且最终回到调度中心,出发时调度车上公共自行车数量为0(实际中若调度中心储备有公共自行车,可以将调度中心看作由虚拟的一个调度中心与几个租赁点组成,调度中心与这几个租赁点间距离及费用均为0)。
3)lij表示租赁点i到租赁点j之间的距离。如果2个租赁点之间无法直接到达,其值为无穷。由于城市道路通行条件限制租赁点i到租赁点j的距离lij不等于租赁点j到租赁点i的距离lji,即lij≠lji。
4)xij为调度车路线安排。当调度车经由租赁点i到租赁点j时,xij取1;否则,xij取0。
5)租赁点i的车辆调配需求为di(i=1,2,…,n),且di
为便于计算,将调配区域划分为m个子区域,每个子区域由1辆调度车调配,求解全局最优问题就转化为求解局部最优问题。
1.1 不带时间窗的公共自行车调配路径优化模型
由于平峰时车辆调配不考虑时间约束,因此以调配成本最小化为目标,建立不带时间窗的公共自行车车辆调配路径优化模型,对平峰时车辆调配或早晚高峰前预调配的调配路径进行优化。
考虑该问题的约束条件和优化目标,车辆调配路径的数学模型如下:
目标函数为
(1)
约束函数为
0≤dj+rj≤Q
(2)
(3)
(4)
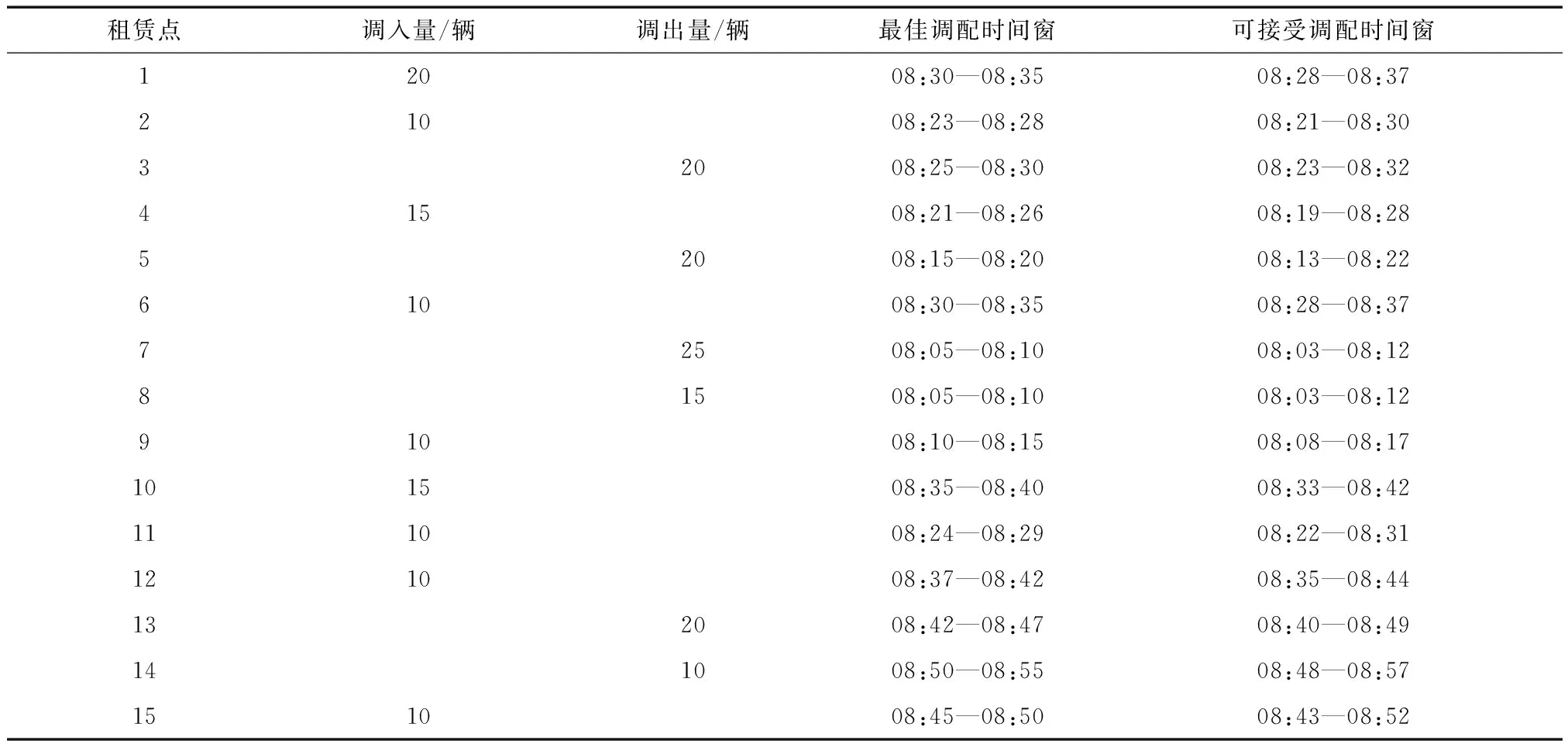
式中:Z为车辆调配的费用;co、ct、cb、cv分别为调度车每千米损耗费用、每千米时间费用、每千米油耗费用、调度车的固定费用;rj(1 式(2)保证调度车不超载,并且在服务下一个租赁点时车上有足够的自行车对其进行服务;式(3)保证从调度中心出发的调度车回到调度中心;式(4)保证调度车只对租赁点服务1次。 与平峰时段借还需求不同,高峰时段需求量大, 此时将以满足需求者要求为目标,车辆调度问题的优化目标中费用问题就不是考虑的重点。由于需求者在高峰时借还车要求可能会被拒绝,因此,为使租赁点拒绝需求者借还要求次数最低,设定一个调配时间窗。在这时间窗内租赁点不会出现无车可借或者无停车桩可还车的情况,调度车对其进行车辆调配就不会有需求者借还要求被拒绝的情况。为使需求者借还的要求拒绝率最低,调度车尽可能地在租赁点所要求的时间窗内对其进行车辆调配。这个时间窗是租赁点最佳调配时间。实际车辆调配过程中,租赁点所要求的最佳时间窗可能无法满足,因此将最佳调配时间窗扩大为可接受调配时间窗。若调度车在此时间范围内对其进行调配,只有少数需求者借还要求被拒绝,租赁点对此可以接受。本文通过引入租赁点满意度对需求者借还要求被拒绝率进行定量表达。租赁点满意度越大,需求者借还要求被拒绝率越低,因此高峰时公共自行车车辆调配路径优化模型是以租赁点满意度最大为目标建立的。 满意度函数是用来衡量租赁点对调度车调配工作的满意程度。如图1所示,(Ci,Di)代表租赁点最佳调配时间范围,(Ai,Bi)代表租赁点可接受的调配时间范围。 图1 软时间窗 当调度车到达租赁点i的时间ti∈(Ci,Di)时,租赁点i对此次的调配服务满意度fi(ti)最大,且fi(ti)=1;当达到时间ti∈(Ai,Ci)或者(Di,Bi)时,租赁点i对此次的调配服务满意度fi(ti)介于0与1之间;当到达时间ti (5) 因此,该问题的数学模型如下: 目标函数为 (6) 其中 (7) 约束条件为: 0≤Qi≤Q (8) (9) (10) (11) 式中:Z为最大满意率;T为时间轴;N(t)为t时刻,所有未被调配租赁点、新增需要服务的点和停车场的集合;M(t)为t时刻,所有调配完成的租赁点的集合;tiv为调度车v到达租赁点i的时间;Qi为调度车在租赁点i服务后车上装载的自行车的数量;v0为调度车的行驶速度,高峰时不同道路服务水平存在差异(道路拥堵情况不同),因此每段道路调度车的行驶速度不一致,行驶速度为2个阻力点的行程速度,在实际情况中,调度车每条路段行程速度可以根据历史行程速度回归分析确定。式(8)保证调度车都不超载,并且在服务下一个租赁点时车上有足够的自行车对其服务;式(9)保证任意从调度中心出发的车都要回到调度中心;式(10)保证对任意由调度车调配的租赁点j必定有另一个(而且只有一个)租赁点(包括调配中心)i;式(11)保证对任意由调度车调配的租赁点i必定有另一个(而且只有一个)租赁点(包括调配中心)j。 公共自行车车辆调配路径优化问题属于图论问题,也是组合优化问题,无法准确的求解,只能采用近似算法求得近似解。一般用于解决此类问题的方法有蚁群算法、禁忌搜索算法和遗传优化算法等[16]。虽然这几种现代优化算法均可用于求解;但由于城市公共自行车租赁点数量规模大,采用禁忌搜索方法求解时,计算机运算时间将较长,因此蚁群算法与遗传算法较为合适求解调配路径优化问题。由于本问题属于带容量约束的旅行商问题,而蚁群算法在旅行商问题中的应用较为广泛,并且不带时间窗的公共自行车车辆调配路径优化模型和基于滚动时域的公共自行车车辆调配路径优化模型均可采用蚁群算法求全局近似最优解;因此,本文采用蚁群算法作为求解算法。 运用蚁群算法求解模型的关键步骤设计如下。 1) 解构造图。蚁群算法的关键问题之一是如何将要解决的问题映射为解构造图,通过人工蚂蚁在该图从起点上行走到终点的路线从而得到问题可行解。 图2 公共自行车车辆调配路径优化蚁群算法构造图 图2是公共自行车车辆调配路径优化蚁群算法构造图。其中:实数1、2、3表示调度车所行使的区间步骤;Di表示租赁点i;dij表示租赁点Di与租赁点Dj之间的距离;虚线框中的租赁点表示在确定前一个租赁点后,调度车在现有可调出公共自行车能力及现有可调入公共自行车能力条件下,满足各项约束后可选择的租赁点去向集合;黑实线表示调度车行走路径。 3)信息素的表示、初始化及更新的原则。信息素τij是指调度车去往租赁点Di的期望度。 (1)信息素的初始化。为在迭代的初期扩大蚂蚁在解空间的搜索范围,解构造图中所有的实边上的信息素均被初始化为τmax,即τij(0)=τmax。图中所有的虚边为辅助边,不起决策作用,因此虚边上没有信息素。 (2)信息素更新原则。信息素的更新原则为: τij(t+1)=(1-ρ)τij(t)+Δτij (12) (13) 式中:ηij是启发式信息,是指调度车自租赁点Di至租赁点Dj的期望度,在模型1中ηij=1/dij,在模型 2中ηij=1/tij;0≤∂≤1表示τij、ηij在构造解时的作用程度。当迭代次数达到上限时,终止算法,输出结果。算法流程如图3所示。 step1:初始化参数,如输入租赁点距离dij、租赁点间行程时间、租赁点自行车数qi等基础数据,初始化蚂蚁数目K、迭代次数M、参数Q、∂、η、τ、ρ等蚁群算法参数。 step2:在0点放置m只蚂蚁。 step4:判断是否走完所有租赁点。若是,则转到step5;若否,则此转到step3。 step5:判断m只蚂蚁是否都走完所有租赁点。若是,则转到step6;若否,则转到step3。 step6:根据信息素更新原则更新信息素矩阵,即每条边上信息素的量。 step7:判断是否满足迭代条件。若是,则输出最优结果;若否,则转到step2。 图3 公共自行车车辆调配路径优化模型算法流程图 以成都市金牛区的公共自行车租赁点为对象进行算例分析。金牛区15个自行车租赁点之间行驶的最短距离如表1所示。 表1 各租赁点之间距离 m 表1(续) m 假设考虑道路交通条件等影响因素,调度车的行程速度为20 km/h,则每个租赁点之间行程时间如表2所示。 表2 各租赁点之间调度车的行程时间 min 1)平峰。 每个租赁点需要调配的自行车数量见表3。 表3 早高峰前每个租赁点需要调配的自行车数量 根据确定的租赁点调配量,首先采用贪婪算法,求得早高峰前车辆调配的初始可行路径为0-2-1-8-10-6-9-5-3-4-7-13-14-15-11-12-0,初始行驶路程为20.4 km。假设调度车每千米损耗费用co为0.26元,每千米时间费用ct为0.1元,每千米油耗费用cb为调度车每千米消耗燃油费用,一般按照汽车每百千米油耗计算,如调度车油耗为8.5 L/100 km,0号柴油价格为7.4元/km,则 为cb为0.629元/km,调度车的固定费用cv为49.1元[17]。此时车辆调配费用为69.3元。运用模型1对调配路径进行优化,采用蚁群优化算法求解,利用MATLAB软件编程运算,如图4所示。优化后行驶路径为0-13-10-7-5-6-1-2-4-8-9-11-12-3-14-15-0,优化后行驶路程为10.5 km,车辆调配费用为59.5元,优化后行驶路程比初始行驶路程减少了48.5%,费用减少14.1%,如表4、图4所示。 表4 早高峰前预调配路径方案比较 图4 早高峰前预调配路径MATLAB软件运算结果 2)早高峰。 假设根据早高峰期租赁点历史借还需求规律以及信息管理系统采集的数据,得出早高峰期每个租赁点的需要调配量及调配时间窗,如表5所示。 表5 早高峰每个租赁点需要调配的自行车数量及调配时间窗 假设调度车对每个租赁点自行车调配时间均为2 min,则根据早高峰时租赁点需要调配的量,首先采用贪婪算法,求得早高峰期初始可行路径为0-7-8-9-10-5-4-3-2-6-11-13-15-14-1-0,租赁点满意度为5.03。运用模型2对调配路径进行优化,采用蚁群优化算法求解,利用MATLAB软件编程运算,如图5所示。优化后行驶路径为0-8-9-5-2-3-11-12-13-15-10-14-6-7-4-1-0,租赁点满意度为8.165,优化后满意度比初始满意度提高了62.3%。 图5 早高峰时调配路径Matlab软件运算结果 将不带时间窗的调配路径优化模型与基于滚动时域的调配路径优化模型进行比较发现:采用滚动时域的优化模型得到的调配总路径为14.78 km,比采用不带时间窗模型的最优路径增加28.9%;但是将不带时间窗模型的最优路径运用于基于滚动时域的优化模型,其满意度为5.382,比基于滚动时域模型的最优满意度减少34.1%。可见,为满足不同时刻的最大需求,应采用不同的模型,才能使利益最大化。同时考虑使调配费用最小与满意度最高,建立公共自行车调配路径优化模型,使该模型均适用于平峰和高峰,是本文下一步研究的问题。 本文从高峰时段和平峰时段的调配需求出发,分别建立不同目标的优化模型,并运用蚁群算法对其求解。通过算例分析表明,该模型具有良好的适用性。在实际公共自行车调配中,调度车的行程时间不仅与租赁点之间的距离有关,还受道路交通条件影响,本算例采用的是较为理想状态;因此在实际调配中应根据实际路况调整调配路径。 公共自行车产生调配问题的一个原因就是租赁点规划布设不合理。目前缺乏科学系统的理论指导租赁点的规划与建设,导致租赁点建成后借还量与规划时预测量存在较大差距,使得后期调配工作任务繁重;因此,把公共自行车租赁点规划布设与路径调配问题统一研究仍需进一步研究讨论。 [1]王志高,孔喆,谢建华,等. 欧洲第三代公共自行车系统案例及启示[J]. 城市交通,2009,7(4):7-12. [2]Demaio Paul. Smart Bikes:Public Transportation for the 21 Century [J]. Transportation Quarterly,2003, 57(1):9-11. [3]Pinand Antoine, Santos Canals Mare. Copenhagen: How Bicycles can Become an Efficient Means of Public Transportation[EB/OL].[2013-08-10].http://hdl.hand le.net/1800/2122. [4]Andreas Kaltenbrunner, Rodrigo Meza, Jens Grivolla, et al. Urban Bicycles and Mobility Patterns: Exploring and Predicting Trends in a Bicycle-based Public Transport System[J]. Pervasive and Mobile Computing,2010(4):455-466. [5]耿雪,田凯,张宇,等. 巴黎公共自行车租赁点规划设计[J]. 城市交通,2009,7(4):21-29. [6]韩惠敏,张宇,乔伟. 里昂公共自行车系统[J]. 城市交通,2009,7(4):13-20. [7]何流,陈大伟,李旭宏,等. 城市公共自行车租赁点布局优化模型[J]. 武汉理工大学学报:交通科学与工程版,2012,35(1):129-134. [8]李婷婷. 城市公共自行车租赁点选址规划研究[D]. 北京:北京交通大学, 2010. [9]何博. 城市公共自行车系统的应用研究[D]. 成都:西南交通大学, 2012. [10]龚迪嘉,朱忠东. 城市公共自行车交通系统实施机制[J]. 城市交通,2008,6(6):27-32. [11]龚迪嘉. 公共自行车交通系统在上海和长沙的应用机制研究[D]. 长沙:湖南大学,2009. [12]Parkin J, Wardman M, Page M. Estimation of the Determinants of Bicycle Mode Share for the Journey to Work Using Census Data[J]. Transportation,2008, 35(1):93-109. [13]董红召,赵敬洋,郭海锋,等. 公共慢行系统的动态调度建模与滚动时域调度算法研究[J]. 公路工程,2009,34(6):68-75. [14]刘登涛,方文道,章坚民,等. 公共自行车交通系统调度算法[J]. 计算机系统应用,2011,20(9):112-116. [15]柳祖鹏,李克平,朱晓宏. 基于蚁群算法的公共自行车站间调度优化[J]. 交通信息与安全,2012,30(4):71-74. [16]陈文兰,戴树贵.旅行商问题算法研究综述[J]. 滁州学院学报, 2006,8(3):1-6. [17]张建国. 城市公共自行车车辆调配问题研究[D]. 成都:西南交通大学,2013.1.2 基于滚动时域的公共自行车调配路径优化模型

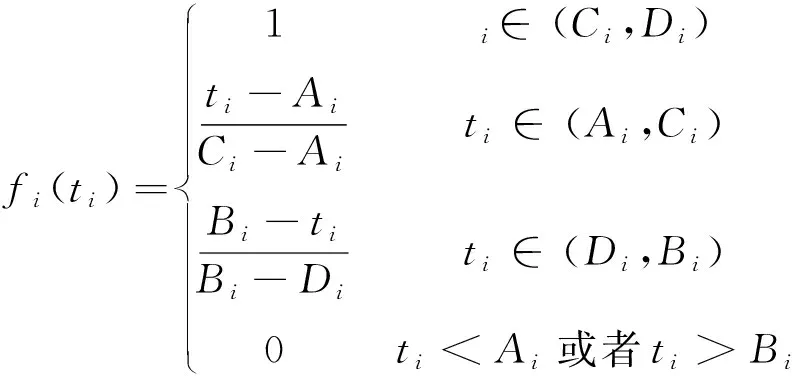

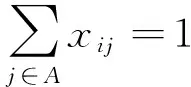
2 算法设计


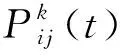

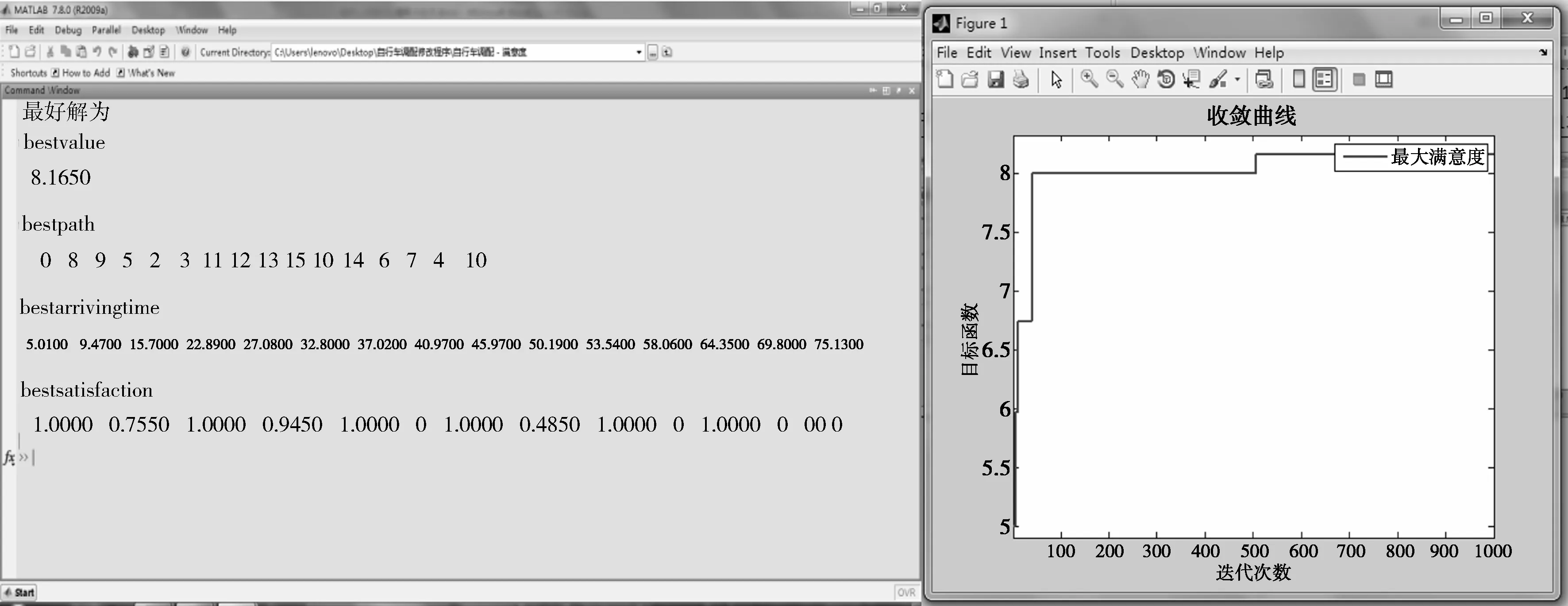
3 算例分析






4 结束语
