相对时差超声法检测微量SF6浓度及FPGA实现

(西华大学电气信息学院，四川 成都 610039)

SF6具有优异的绝缘和灭弧性能,在电力、工业生产等场合得以广泛应用。在实际操作中，由于设备的制造、安装质量差异和设备老化等因素，不可避免地会出现SF6的泄漏[1]。泄漏的SF6被电击后将产生有毒气体，这不仅会危及电力安全，对大气环境造成极大危害，而且会造成低层空间缺氧，使人窒息[2]；因此，准确检测空气中SF6浓度，对确保设备可靠运行、保证现场工作人员的人生安全和保护大气环境都具有重要意义[3]。

目前对SF6浓度进行检测的方法有很多，如红外吸收法、化学分析法、电晕放电法、超声检测法等。红外吸收法使用的仪器体积庞大、复杂且造价高，所以红外吸收法难以被推广；化学分析法不宜在线检测；电晕放电法使用的传感器寿命较短，不能长期稳定工作[4]。超声法检测由于具有精度高、稳定性好且不存在二次污染等优点，而得以广泛应用。超声波检测气体浓度的方法很多，但从原理上来看，仅有2类：时差法和时间差分法(又称为相位差法)。时差法易于实现，但不能达到电力系统对SF6气体浓度的检测精度要求。时间差分法虽然检测精度高，但在实际应用中条件苛刻，不易于实现，且浓度的测量范围也比较受限。

本文结合时差法和时间差分法各自的优点，基于超声技术提出一种成本低、结构简单、可靠性高的微量气体浓度检测方法——相对时差法，并使用现场可编程门阵列(FPGA)器件实现SF6浓度的相对时差法检测。仿真结果表明，该方法的测量精度可达到10-5，相对误差不大于1%。

1 相对时差法检测SF6浓度的原理

时差法检测SF6浓度的原理是固定超声波收发距离，测出超声波在混合气体中传播的时间，再根据温度、气体参数等条件，计算出被测气体浓度[2,4]。因为超声波传感器收、发头的固有特性，在接收端不能检测出前面几个超声波脉冲，所以时间测量误差过大，不能达到电力系统对SF6气体浓度的检测精度要求。

时间差分法检测SF6浓度的原理是采用2组声程相同的超声波传感器，一组测超声波在背景气体，如空气中的传播时间，另一组测超声波在被测气体，如混合气体中的传播时间，利用两者时间的差值计算出被测气体的浓度[5]。这类方法最高精度可达10-6[5-6]，完全能满足SF6浓度检测要求，但这是在2组超声波传感器特性、声程、背景气体和被测气体的温度完全相同的情况下获得的，在实际应用中，这种条件是不可能满足的。另外，检测还要满足2个传播时间之差不能超过1个脉冲周期，这大大限制了它的测量范围。

在利用相对时差法检测微量SF6浓度时，只需要1组超声波传感器。图1为相对时差法超声检测原理示意图。在发送端，发射一串超声波脉冲串。在相同温度、声程的条件下，超声波脉冲串分别经过空气和被测混合气体到达接收端。从图可以看出，由于超声波收发头起振和超声波在气体中传播能量衰减特性，导致前几个脉冲检测不出来，使得所测收发脉冲时差会比真实值大Tx。Tx是未知量，它与声程、温度等有关。先在检测SF6浓度前，测出介质为空气时的收发脉冲时差T0,k，再测混合气体收发脉冲时差T1,k。由于在2次检测收发脉冲的时差时，声程、温度都一样，且检测的是微量气体，故2次测试的Tx值不变。相对时差

ΔT=T1,k-T0,k

(1)

从式(1)可以看出，ΔT与Tx无关，从而削除了超声波收发头特性带来的误差。当被测气体浓度很小时，其浓度公式[6]可近似表示为

(2)

式中：L为声程；cR为超声波在空气中的声速；MO为SF6的摩尔质量；MR为空气的摩尔质量；x为SF6的浓度。将式(1)代入式(2)，整理可得

(3)

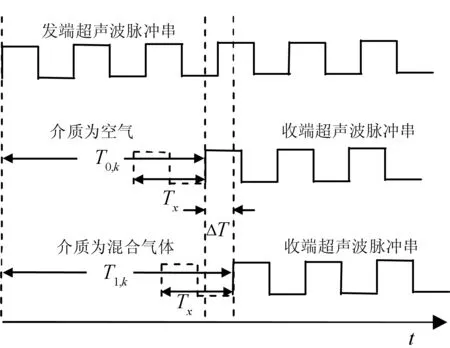
图1 相对时差法超声气体检测原理示意图

相对时差法检测SF6浓度的误差主要来源于电路所采用的时钟。这种误差同样也存在于其他超声波检测气体浓度方法中，只是很多文献没有提到。在接收端，收到的超声波信号与电路时钟并不同步，必定会产生亚稳态。如果检测电路采用FPGA实现，这一状态将持续约3 ns[7]；因此，电路时钟周期必须大于3 ns 。经D触发器采样、同步后，得到稳定信号，这样产生ΔT的最大误差为1个时钟周期Tclk。由此，被测气体误差Δx的公式为

(4)

设定L=10 cm，MR为28.96 g /mol，MO为146.06 g/mol，不同温度下超声波在空气中的速度cR为

(5)

式(5)中的T为热力学温度。将式(5)代入式(4)得到Tclk与Δx的关系式。

Tclk与Δx的关系由图2给出。从图可以看出：SF6气体浓度误差随时钟周期增加而线性增大；当温度越高，这一误差随时钟周期增加而更快的增加。当环境热力学温度为350 K、时钟周期为100 ns时，误差最大，为0.185 4×10-3。需要指出的是，无论时差法还是时间差分法，都有这种误差存在，只是相关文献未讨论。表1给出了相对时差法与另外2种检测方法的误差比较结果。比较时考虑了3种方法的实际应用特点，工作环境温度为310 K。为公平比较，3种方法的误差计算都采用文献[7]的公式。时差法不需要2路超声波，故没有2种气体温度与2路超声波脉宽差引起的误差；而时间差分法测的是2路超声波相对时间差，不需要在收端测超声波脉冲串的起始位置，因此没有未检测出超声波脉冲引起的误差。由表1可以看出：由任一因素引起的3种检测方法的误差中，相对时差法都是最小的，最后统计的误差总和自然也是它最小；时间差分法采用2组超声波收发器，检测设备复杂，总误差却比相对时差法大1个数量级；时差法检测误差过大，不宜用于微量气体浓度检测。

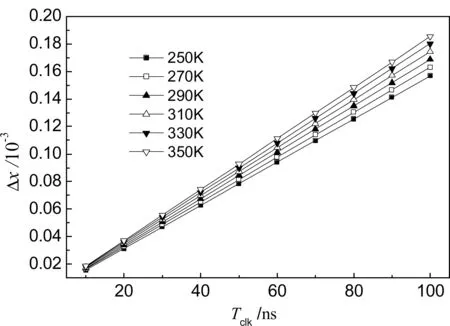
图2 Tclk与Δx的关系

表1 3种检测方法的误差比较

2 相对时差法的FPGA实现

相对时差法检测SF6浓度的主要功能是由Altera公司的Cyclone II EP2C8Q208C8完成。该器件具有成本低、速度快、逻辑单元密度高等优点[8]。FPGA实现检测的功能模块划分如图3所示。器件工作分为2种模式：T0,k检测模式和SF6浓度检测模式。这2种模式可以通过按键来选择。器件首先工作在T0,k检测模式下。设备放置在空气环境中，温度由253 K升到333 K(即由-20 ℃升至60 ℃)，T0,k/T1,k检测模块在温度每上升0.5 K就测1个T0,k值。数据转换模块将ds1820温度传感器测得的数据处理并转换为并行地址。这样，FPGA就可以将温度与测得的T0,k值对应起来，存入T0,k存储模块中。为避免掉电引起T0,k数据丢失，该设备采用不间断电源。T0,k检测模式结束后，器件就可以正常工作在SF6浓度检测模式下。在这工作模式下，FPGA首先根据测得的温度值，在T0,k存储模块中找出对应的T0,k，然后由T0,k/T1,k检测模块利用收发超声波脉冲串测得T1,k，再由SF6浓度计算模块根据T0,k、T1,k和温度值(用于计算空气中的超声波速度)按式(3)计算出SF6的浓度，最后将浓度数据由显示模块转换送给数码管显示。

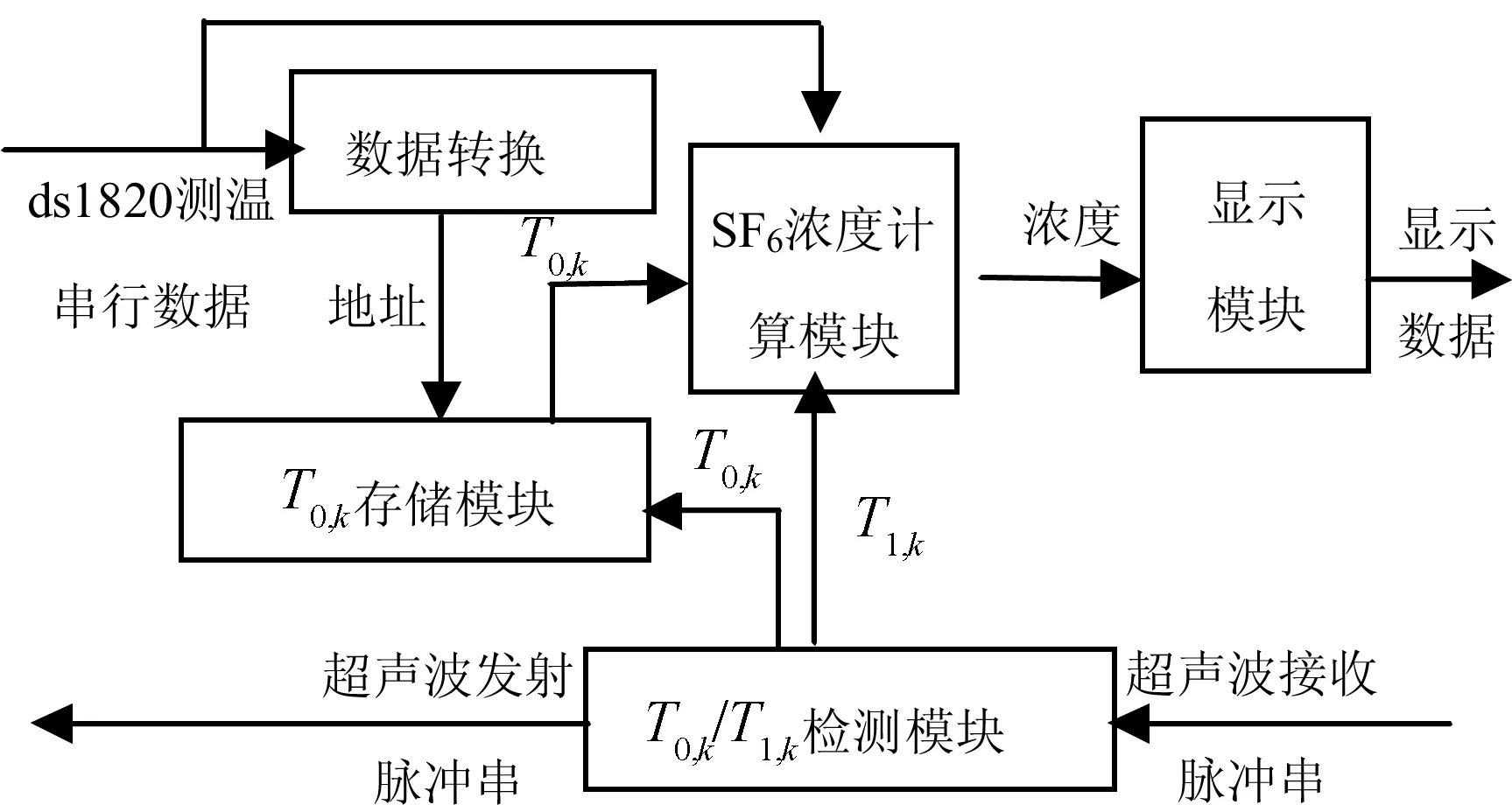
图3 FPGA实现SF6浓度检测功能模块图

在FPGA设计中，最重要的是SF6浓度计算模块。温度变化范围为253 K到333 K，如果每0.5 K取1个值，共有161个值。如果用0到160分别表示253 K到333 K，只需8位数据总线表示即可。由式(3)可得，在微量浓度下，T1,k-T0,k与x成正比，每个温度值对应1个(2cR/L)/[(MO/MR)-1]；因此，可以事先将这161个值存于ROM中， 运算时FPGA先根据由环境温度转换而成的ROM地址，从ROM中找出Z=(2cR/L)/[(MO/MR)-1]的值，再由FPGA获取的T1,k、T0,k的值计算出T1,k-T0,k，最后按式(3)计算出结果x。这一实现方案充分考虑到FPGA有丰富的片内RAM，可以非常容易地配置为ROM，从而实现关键的运算功能，无需耗费大量的逻辑单元，大大提高了速度。经Quartus II软件综合后，电路占用器件逻辑资源小于1%，占用存储单元仅为2%，器件工作速度可以达到154 MHz以上。

FPGA计算SF6浓度的仿真结果，如图4所示。仿真温度设为300 K，换为ROM存储地址后T为94，对应的参数Z的值为1 796.9，经过T0,k/T1,k检测模块得出T0,k、T1,k的值在虚线a处分别为2.881 0×

10-4s和2.881 5×10-4s，在虚线b处FPGA计算出对应的x值为8.584 5×10-5。与实际SF6浓度8.665 1×10-5的相对误差为0.930 2%，不超过1%，这和用公式(3)的结果完全一致。

图4 相对时差法测SF6气体浓度的仿真结果

3 结束语

本文以混合气体中SF6浓度测量为研究背景，结合时差法和时间差法的优点，利用相对时间差法进行分析，得出二元混合气体中浓度、声速和相对时间差存在的函数关系。仿真结果表明，利用超声技术的相对时差法测量SF6气体浓度具有电路简单、成本低的优点，其测量精度能达到10-5，相对误差不大于1%。相对时差法不仅适用于空气中FS6浓度的测量，而且在修改公式中的参数后能用于检测其他二元混合气体浓度；因此，它在微量气体浓度测量领域中，具有广阔的应用前景。

[1]郭利民，赵红梅，吕运朋，等．SF6气体泄漏环境在线智能检测系统的设计[J]． 仪表技术与传感器，2011 (8) : 76-78．

[2]蔡艺剧，黄勇，尹遴，等.一种新的微量气体浓度检测方法[J].化工自动化及仪表，2012,39(4)：477-479.

[3]朱昌平，单鸣雷，刘永富，等． 基于 CPLD 的SF6微量气体浓度检测仪[J]． 仪器仪表学报，2005，26(s1) : 448-449．

[4]王明伟，姚展．一种二元混合气体浓度超声测量仪的设计[J]．计算机测量与控制，2010，18(12) : 2908-2910．

[5]张晓花，朱昌平，单鸣雷，等． 超声宽量程微量气体浓度检测的仿真研究[J]． 声学技术，2008，27(1):40-43．

[6]单鸣雷，王月庆，朱昌平，等．微量浓度二元混合气体的超声检测研究[J]．压电与声光，2009，31(1):129-131．

[7]阳小明．高速异步FIFO的实现[J]．西华大学学报：自然科学版，2005，24(4):77-79.

[8]宋泽琳，郑恩让，马令坤． 基于 FPGA 的电力系统谐波检测算法研究及实现[J]． 化工自动化及仪表，2011，38(6) : 713- 717．