金团簇二维到三维的结构转变和电子特性的理论研究

(西华大学物理与化学学院,四川 成都 610039)

金是人类较早发现和利用的金属之一，块状的金有很强的延展性，熔点1 063 ℃，化学性质非常稳定，所谓“烈火见真金”正是由此而来。随着科学技术的发展，人们对金的认识也越多。许多研究已经表明：对于一氧化碳的氧化、苯乙烯和甲醇的选择性氧化、丙烯的环氧化等，纳米Au团簇是一类较好的催化剂[1-3]，而且，其独特的物理化学性质在光电信息处理、纳米电子器件等方面也有着广阔的潜在应用价值[4]。

为了理解团簇结构与性质之间的关系，Au团簇的研究一直受到人们广泛的关注，然而，关于基态金团簇的结构由二维到三维的转变，究竟是从多少个Au原子开始的，至今仍无一个定论。毛华平等[5]利用密度泛函方法和Wang等[6]在LDA近似下结合遗传算法，发现二维结构到三维结构的转变出现在7个金原子处。Olson等[7]利用CCSD(T)、DFT、MP2方法优化了Au6和Au8团簇的几何结构，推测二维到三维构型的转变应该出现在8个Au原子形成的团簇；但是Han[8]在此基础上重新计算后认为平面Au8比其三维结构能量更低。Fa等[3]和Eva等[9]的研究又认为金团簇的基态结构从平面到立体的转变发生在Au12和Au13团簇，而Ajanta等的计算显示2～13个Au原子团簇的基态结构都为平面结构[10]。最近，Idrobo等[11]利用密度泛函理论研究显示，金团簇原子数小于14的基态结构均为平面结构。金团簇的基态结构从二维到三维的转变究竟在何处，仍需进一步的计算和实验来验证。

在本文中，我们将利用密度泛函理论系统地研究Aun(n=2～14)团簇的几何结构和电子特性，这对进一步了解金团簇结构与催化性能的联系具有较重要的理论和实践意义。

1 计算方法

早期的研究已经证明密度泛函PW91与TZVPP基组对于金团簇的物性研究是一种较好的计算组合[2,12]。为了搜索到金团簇的最稳定结构，许多的初始构型被使用，其中包括各种线性、平面和立体结构。考虑到自旋极化的影响，本文对每一种构型都在相应的自旋多重态下做了几何结构优化和频率分析，认为只有振动频率不存在虚频的异构体才是稳定的结构。所有计算中收敛极限设置是：能量为10-8a.u.；最大位移为1.8×10-3a.u.，其方均根偏差为1.2×10-3a.u.；最大力为4.5×10-4a.u.，其方均根偏差为3×10-4a.u.。该理论级别和其他计算方法的比较情况如表1所示。可以看出PW91/TZVPP计算值与实验结果符合较好。

表1 不同密度泛函方法下基态Au2的计算值与实验 结果

2 结果与讨论

2.1 几何结构

对于小的Aun(n=3～6)团簇，本文的计算结果表明其基态结构都为平面构型，而且它们的最低自旋态都比高自旋态能量低。这与前人的研究结果一致，所以图1仅显示了其基态结构。对于Aun(n=7～14)团簇，许多异构体被得到，图1给出了每一大小团簇的基态结构和 3个能量最接近基态的异构体，并按能量从低到高的顺序编为na、nb、nc和nd，同时，每个结构下面给出的3个参数依次为对称性、自旋态和相对基态的能量差。

Au7团簇的基态结构如图1(7a)所示，为平面构型，这与Idrobo等[11]的计算结果一致。至于毛华平等报道的五角双棱锥基态结构[5-6]，在本文的理论级别下其能量比7a高0.77 eV。第2个异构体是D2h对称的环状平面结构，由于Jahn-Teller效应，该Au六环相对于D6h有一很小的畸变；第3、4异构体是2个三维结构。对于Au8团簇的基态结构，Olson等利用CCSD(T) 方法推测为三维结构[7]，但Han的计算结果是二维结构[8]；本文的DFT计算支持Han的结果，为D4h平面结构。至于Au8团簇的三维异构体，我们的计算显示其能量都比8a高。

随着团簇的增大，许多平面和立体结构被优化。得到的Aun(n=9～11)团簇的低能异构体明显偏于平面结构，如图1所示，其基态结构为9a、10a、11a。在其余的平面异构体中，9b仅比9a高0.01 eV，10b和10c是2个简并的异构体，11a—11d都包含一个类似于9a的结构。至于n=9～11的三维异构体，我们的优化显示：它们的能量都比各自的列在图1中的平面结构的能量还要高。

对于Aun(n=12、13)团簇，Eva等[9]计算得到的基态结构为三维结构，但是Ajanta等[10]的计算结果为平面结构。鉴于此，我们对前人的所有结构进行了重新优化，同时又对以前没有考虑的二维和三维结构进行了优化。结果显示Au12和Au13团簇的前4个低能异构体均为平面构型，如图1中的12a—13d所示，而前人得到的立体结构在本文的理论级别下均比图1中相应的平面结构更不稳定。

在Au14团簇的结构优化中，超过30个平面和立体结构被获得。Au14团簇的基态结构为三维扁笼状形结构，如图1中的14a所示，其他3个低能异构体均为平面结构，其中第2个异构体仅比基态高0.05 eV。另外，Idrobo等[11]计算得到的Au14团簇的基态结构也是一个三维结构，但他们的基态结构不同于本文获得的。我们的计算显示他们的基态结构有一个8.5 cm-1的虚频，是一个不稳定的结构，只有转变成14a才是一个稳定的结构。

由以上对计算结构的分析可以看出，Aun团簇的基态结构在n=3～13范围内都为平面结构，当n=14时，开始从平面结构转变成立体扁笼状形结构。

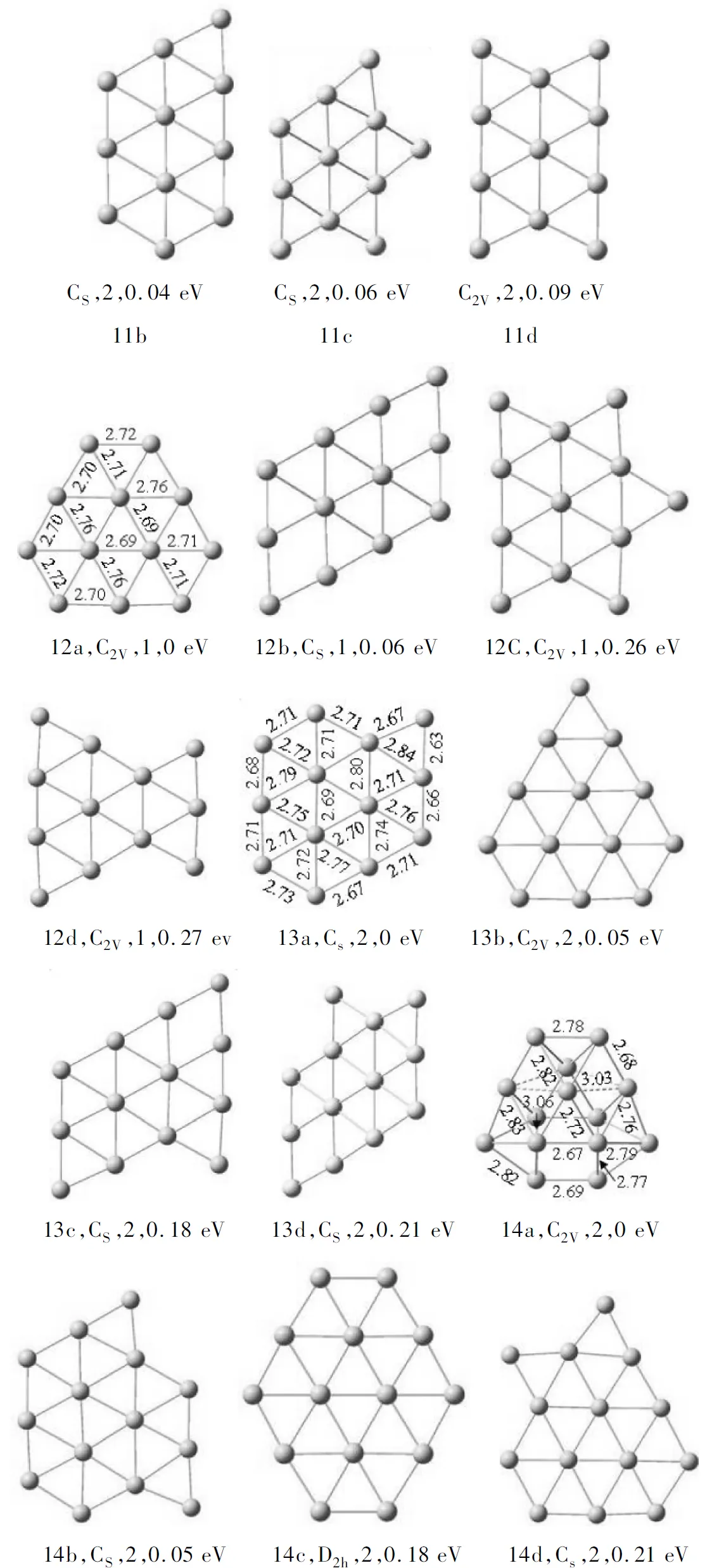
图 1 Aun(n=3～14)团簇的基态结构和对于n≥7的3个低能异构体

2.2 电子特性

团簇生长过程中由于电子的耦合导致能量变化的情况，可通过计算原子平均结合能(Eb)来反映，对于基态Aun团簇，其计算公式为

(1)

式中E(Au)、E(Aun)分别表示基态Au原子和Aun团簇的能量。图2给出了Aun团簇的原子平均结合能随Au原子数的变化关系。可以看出，从n=2～6 原子平均结合能增长较快，随后趋于平缓。这表明大的金团簇原子之间的结合力比小的金团簇更强。

团簇的稳定性随团簇大小的变化，理论上可利用团簇的二阶能量差分来界定。二阶能量差分较小，表明该团簇的稳定性较低，反之则稳定性较高。对于基态Aun团簇，二阶能量差分(Δ2E)定义为

Δ2E(Aun)=E(Aun+1)+E[(Aun-1)-2E(Aun)。

(2)

式中E分别表示相应基态团簇的能量。图3显示了Aun团簇的Δ2E随团簇n的变化的函数关系。可以看出，基态偶数原子Aun团簇的Δ2E值大于奇数Aun团簇，随原子数n表现出奇偶变化。说明n为偶数的Aun团簇在稳定性方面高于邻近的n为奇数的Aun团簇，这可能源于Aun团簇价电子的奇偶交替变化。

图 2 Aun团簇的平均结合能

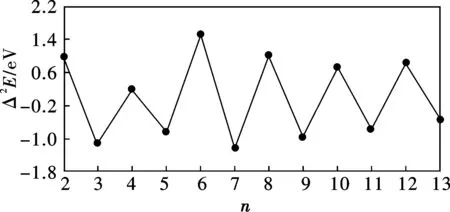
图 3 Aun团簇的二阶能量差分

团簇中电子的最高占据能级(HOMO)与最低未占据能级(LUMO)之间的能量差是反映团簇中价电子从占据能级向未占能级跃迁的一个重要参数，决定着团簇在化学反应中的活性。如果该能级差较小，则化学活性较高；能级差较大，则化学活性较低。图4展示了基态Aun团簇的HOMO-LUMO能级差随Au原子个数的变化关系，偶数金团簇的能级间隙大于奇数金团簇，这说明奇数金团簇的化学活性比相邻偶数金团簇高。

图 4 Aun团簇的HOMO-LUMO能级间隙

团簇的电子亲和势(EA)和垂直电离势(VIP)是反应团簇内部电子结构和实验上可以测定的2个重要物理量。电子亲和势为中性团簇的能量与具有相同结构参数且带一个单位负电荷的阴离子团簇的能量差；垂直电离势为中性团簇的能量与具有相同结构参数且带一个单位正电荷的阳离子团簇的能量差。我们计算得到的金团簇的EA、VIP和实验值如表2所示，同时也显示在图5中。可以看出：金团簇EA的计算结果与实验值符合较好，且都表现出奇偶振荡性；除Au3团簇外，其他金团簇VIP的理论值与实验结果保持了相同的变化趋势。这说明偶数金团簇不易失去电子，奇数金团簇容易得到电子，也进一步证明了本文理论级别对于金团簇研究的适用性。

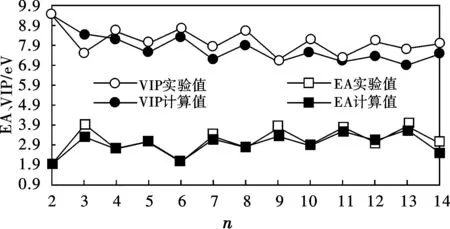
图 5 Aun团簇的EA、VIP计算结果和实验值的比较

表2 Aun团簇的EA和VIP的计算值和实验值eV

团簇Au2Au3Au4Au5Au6Au7Au8Au9Au10Au11Au12Au13Au14EA计算值1.893.312.663.052.093.192.763.362.873.593.153.652.47EA实验值1.923.882.703.062.063.402.733.813.893.763.033.912.94VIP计算值9.508.448.287.578.417.207.937.067.557.067.386.917.47VIP实验值9.507.508.608.008.807.808.657.158.207.288.157.708.00

3 结论

本文利用密度泛函PW91方法，研究了Aun团簇的几何结构和电子特性。结果表明：在n=3～13范围内，Aun团簇的基态结构为平面构型，当n=14时，开始从平面结构转变为三维结构；大的金团簇原子之间的结合力强于小的金团簇，偶数金原子团簇的稳定性高于相邻奇数金原子团簇，奇数金团簇的化学活性比相邻偶数金团簇高，且在化学反应中易得到电子。

[1] Haruta M, Kobayashi T, Sano H, et al. Novel Gold Catalysts for the Oxidation of Carbon Monoxide at a Temperature far Below 0oC [J]. Chem Lett, 1987, 2: 405-408.

[2] Die D, Zheng B-X, Zhu B. Geometrical, Electronic, and Magnetic Properties of AunV (n=1-8) Clusters: A Density Functional Study [J]. Mol Phys, 2011, 109: 1709-1716.

[3] Fa W, Luo C, Dong J. Bulk Fragment and Tubelike Structures of AuN(N=2-26) [J]. Phys Rev B, 2005, 72: 205428.

[4] 任娟, 代雯乐, 付欣,等. 金团簇的荧光性质及其生物应用[J]. 化学通报, 2011, 74: 683-687.

[5] 毛华平, 王红艳, 倪羽,等. Aun(n=2-9)团簇的几何结构和电子特性 [J]. 物理学报, 2004, 53(6): 1766-1771.

[6] Wang J, Wang G, Zhao J. Density-functional Study of Aun(n=2-20) Clusters: Lowest Energy Structures and Electronic Properties [J]. Phys Rev B, 2002, 66: 035418.

[7] Olson R M, Varganov S, Gordon M S, et al. Where Does the Planar-to-nonplanar Turnover Occur in small Gold Clusters [J]. J Am Chem Soc , 2005, 127: 1049-1052.

[8] Han Y K. Structure of Au8: Planar or Nonplanar [J]. J Chem Phys, 2006, 124: 024316.

[9] Eva M F, José M S M, Ignacio L G, et al.Trends in the Structure and Bonding of Noble Metal Clusters [J]. Phys Rev B, 2004, 70: 165403.

[10] Ajanta D, Ramesh C D. Structural Electronic Properties of Stable Aun(n=2-13) clusters: A Density Functional Study [J]. J Mol Struc-Theochem, 2008, 870: 83-93.

[11] Idrobo J C, Walkosz W, Yip S F, et al. Static Polarizabilities and Optical Absorption Spectra of Gold Clusters (Aun,n=2-14 and 20) from first Principles [J]. Phys Rev B, 2007, 76: 205422.

[12] Li X B， Wang H Y，Yang X, et al. Size Dependence of the Structures and Energetic and Electronic Properties of Gold Clusters [J]. J Chem Phys, 2007, 126: 084505.