基于Agent的保险系统非对称信息博弈研究

刘 超 赵钦涵

（山东财经大学，山东 济南 250014）

一、引言

保险系统作为金融系统的重要组成部分，集风险性和金融性于一体。保险经营活动中交易双方因各自所处的地位、信息交流的愿望、拥有的资源和保险知识等差异，形成了保险系统信息不对称的现象。信息是市场经济中影响资源有效配置的重要因素，保险系统的买方和卖方都难以获得完全的信息，信息不对称产生了保险逆向选择和道德风险，妨碍了保险机制顺利运转，使保险系统资源配置效率严重降低。信息不对称是根植于保险系统的内生因素，是导致保险系统脆弱性的深层原因。研究如何降低信息不对称，对于降低保险系统的风险积累，缓解保险系统的脆弱性，具有极其重要的意义。

自博弈论诞生以来，针对保险系统信息不对称问题的研究就与博弈论密不可分了。不完全信息博弈论，在信息不对称问题研究中具有天然的优势。然而，虽然博弈论能较好地解决非对称信息问题，但它在理性基础方面采用的是一种“完全理性”的假设。

实际市场中的投资者并非像传统金融理论中所假设的那样，是具备完全信息的。在不具备完全信息条件下的投资者对信息有不同的反应方式，有不同的预测与决策机制，每个投资者在已有的信息下做出预测及投资决策形成了市场价格，反过来市场价格所包含的信息又影响投资者的预测及决策。这样每个投资者根据市场状态的变化及成功者的经验不断地形成新预测规则，并验证与修改预测规则。从而每个投资者的预测规则与市场是协同进化的，且在此进化过程中，投资者的聚集、分化、对信息的非线性反应方式造就了整个保险系统宏观层面上的复杂性。保险系统宏观层面上的复杂性是由微观层面上各个投资者不断适应市场环境造就的，因此保险系统是一个复杂自适应系统。传统的博弈数学模型中最重要的假设就是博弈双方行为人的“共同知识”假设，很明显复杂保险系统中这种假设通常是得不到保证的，对于复杂保险系统中的难题传统博弈论难以有效解决。

与传统的博弈数学研究范式相比，复杂性科学能够全面有效解决非线性、复杂性、动态性问题，而保险系统非对称信息系统恰恰具有非线性、复杂性、动态性等特性，因此复杂适应系统理论恰好可以解决这个困难，实现从均衡经济学理论到非线性经济学理论的跨越。

二、国内外研究现状

对逆向选择问题的研究中，最核心的研究是由罗斯切尔德和施蒂格利茨（Rothchild和Stiglitz，1976）做出的。罗斯切尔德和施蒂格利茨（1976）通过对竞争性保险系统均衡的分析发现，具有不完备信息的竞争性保险系统比具有完备信息的标准模式更为复杂。在施蒂格利茨和阿莫特（Stiglitz和Amott，1988）合作构造的保险系统纯道德风险标准模型中，他们用倒置的因果关系推导出获得高保障的被保险人更容易因为疏于防范将自己置于更大的风险中。R&S模型只讨论了逆向选择单独存在的情况，而在现实中逆向选择与道德风险往往同时存在。沙萨尼翁和基亚波里（A·Chassagnon和P·A·Chiappori，1997）考察了保险系统逆向选择和道德风险并存下的混合标准模型，得出风险与保障之间存在正相关性。

复杂性科学是研究复杂性与复杂系统中各组成部分之间相互作用所涌现出的复杂行为、特性与规律的科学。1995年，霍兰出版了系统阐述复杂适应系统理论的专著——《隐秩序—适应性造就复杂性》，标志着复杂系统理论的创立。CAS理论的核心思想就是“适应性造就复杂性”。20世纪90年代前后国内外学者逐渐将复杂性理论应用到金融研究中。圣菲人工股市模型（SFI-ASM）（1997）的建立，标志着基于Agent建模的金融复杂性研究这个领域正式确立。沙莱和张（Challet和Zhang，1997）建立的少数派博弈模型（Minority Game，MG）是一个同时具备适应性、异质性和反馈特点的确定性系统。此后少数派博弈模型就迅速成为人们研究复杂适应系统、建立金融市场模型的一个重要的范式。李玉丰等（2001）借助Swarm仿真平台研究博弈论的定量化问题，以“囚徒困境”经典模型为实例，通过适应度来求解均衡结果，验证了理论的均衡解。王文举、杨思磊（2002）研究了复杂适应性系统与博弈论的关系，发现二者之间存在诸多相似性：研究在一个给定的环境中智能体（即局中人）相互作用的问题；研究策略互动思想并设计了很好的学习机制等。任韬（2009）以复杂适应系统为基础，使用经济动态模拟方法，对保险活动的主体以及主体的属性和行为进行了分析，提出了建立保险市场经济动态模拟模型的一般方法。

通过文献梳理可以发现，国内学者只是对我国保险系统信息不对称问题的现状作了简要描述，提出一些我国保险实务界针对信息不对称问题的对策，并没有进行深入的理论研究和实证分析，理论研究成果与保险实务上有一定差距。有的学者虽然从信息经济学角度作了分析，但也只是简单介绍了信息经济学中对信息不对称的分类及其表现，没有深入展开研究，更没有构造和分析解决信息不对称问题的对策模型。国外学者虽然对保险系统不对称信息问题进行了大量的实证研究，但在理论基础方面采取的是“完全理性”的假设，分析结果并不能反映现实世界的真实情况。国内学者在应用复杂性科学的理论思想时，更侧重于对保险系统进行定性方面的考察，对保险系统的定量研究虽有突破，但大部分学者还是借鉴国外的研究成果和方法。国外学者在应用复杂性科学的理论思想时，更侧重于进行数量技术层面的实证分析，侧重于对某一个或几个保险系统中的具体问题进行定量研究，缺乏一种宏观层面上的、整体性的系统把握。

三、保险系统中非对称信息博弈模型

（一）保险系统的逆向选择模型

假设在模型中，保险公司为代理人Agent，投保人为委托人Agent，假设条件为：

1.只存在两类风险水平不同的投保人：一类是低风险投保人，其发生该险种条款规定灾难或事故的概率为PL；另一类是高风险投保人，其发生该险种条款规定灾难或事故的概率为PH，且PH＞PL。

2.所有投保人具有相同的效用函数u（x），初始收入为M，最大损失为L。

3.保险公司管理成本为零，保险公司对风险持中性态度，市场中所有参与人以利益最大化为出发点。设保险费率为π，投保人投保资产为Q。

分别考察双方在发生灾害和未发生灾害两种状况下的收益：Y1代表未发生灾害状态下的收入，Y2代表发生灾害状态下的收入。

所以，投保人的收入就是保险公司的支出，保险公司的收益就是投保人的支出，投保人与保险公司的经济利益是相互对立的。

在上述两种风险水平不同的人可能得到的赔偿额相同的情况下，出于自身利益考虑，高风险的投保人总是希望购买低风险型的保险契约，从而以更少的成本获得同样的效用。完全竞争市场上的不对称信息均衡，主要有以下两种：

1.逆向选择下的混同均衡。混同均衡就是指不同类的消费者购买相同的保险合约。假设保险公司提供的保险合同为单一保费率π，∂表示高风险投保人所占的比例，1-∂为低风险投保人所占的比例，则均衡费率Pˉ=∂PH+(1-∂)PL。保险公司的保险费率是根据平均风险水平厘定的，由于PL＜Pˉ＜PH，如图1所示：混合费率下投保人的预算线T过初始点A但介于TH和TL之间。由于高风险投保人在π=PH时的均衡点在45度角平分线上，将在45度角平分线左侧的b点达到最优。同理，低风险投保人将在45度角平分线的右侧达到最优。但是，在这种情况下，投保人选择保险合约b等于告诉保险公司他属于高风险的投保人，因为低风险投保人总是会选择保险合约a，此时，追求利润最大化的保险公司将会提供专为高风险者准备的保险合约K给该投保人。因此，高风险的投保人会伪装成低风险者去选择保险合约a。在逆向选择条件下，高风险类型投保人从混同均衡保单中获得预期效用的增加是以牺牲低风险类型投保人的预期效用为代价的。

但是，保险合约a也不可能是均衡点。在任一点低风险者的无差异曲线都会比高风险者的无差异曲线陡峭，所以在a点，低风险者的无差异曲线必然从上往下穿过高风险者的无差异曲线。因此，在一个完全竞争的保险系统上，混同均衡解不可能存在，如果一家保险公司向投保人提供单一的混合保险合约a，必然会有其他竞争者设计出一个只吸引低风险者的保险合约，从而使得该保险公司面临的投保人事故发生概率并不是P，而是PH，保险公司还是亏损。因而，在完全竞争市场上，混同均衡不可能存在。

2.逆向选择下的分离均衡。如图2所示的保险合约H和保险合约L，此时，高风险的投保人与对称信息均衡下没有区别，在保险合约H下达到效用最大化；若保险公司对低风险投保人提供的合同在45度线与TL的交点上，这时低风险投保人的期望效用与对称信息下相同，而高风险投保人的期望效用比对称信息下更高，于是为防止高风险投保人混同于低风险型投保人，低风险投保人的合同必须在UH（H）之上，即TL线上。在零利润假设下，H和L构成一个分离均衡：高风险类型的投保人选择合同H，低风险类型的投保人选择合同L。

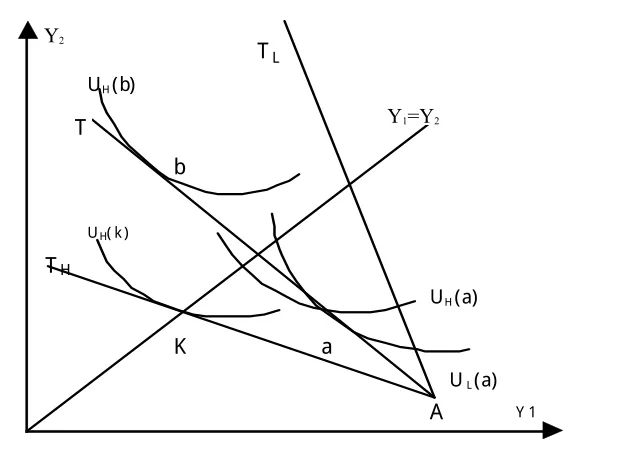
图1：逆向选择下的混同均衡

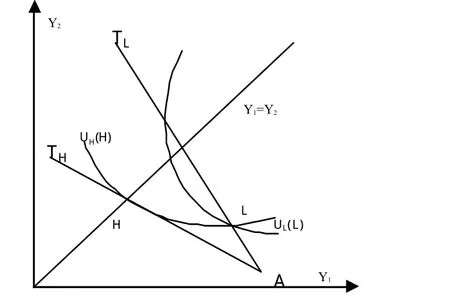
图2：逆向选择下的分离均衡

在存在逆向选择的保险系统上，保险企业针对不同风险水平的投保人设计出不同费率的保险合同，同时，对不同风险水平的保险合同规定不同的保险限额。这样一种分离均衡成为逆向选择的理论解。但与对称信息情况不同的是，在非对称信息下，低风险类型的投保人只能被部分地保险。

（二）保险系统的道德风险模型

假设保险系统上只有投保人和保险公司两个参与者，每一个参与者都希望自己的效用最大化。保险公司追求预期利润最大化，即收取高保费，赔付较低的保险金；而投保人希望以最低的保险价格获得最全面的保险，显然这两者的目标是不一致的。两方参与人在信息方面存在不对称性，投保方对保险标的风险及风险控制状况更了解，而保险公司则对自身的偿付能力和信用状况比投保方有更清楚的认识。博弈双方均采取触发策略，即一旦一方采取不合作的策略，那在接下来的博弈中另一方当事人将一直采取不合作的策略。

图3：保险人与投保人的支付矩阵

图3是重复博弈的一个单阶段博弈。

保险人的期望利润函数为：

其中，X为保费；Y为保险金额；g为发生事故的概率；a，b，c，d均为大于零的常数。

投保人的期望利润函数为

C(g)表示投保人采取防范措施的成本支出，p、q均为大于零的常数。

假设高风险的g2＞低风险的g1，可以得到支付矩阵中各个元素的具体表达形式。

1.3.1 临床数据采集 对所有的受试者进行详细的病史采集和生化指标检测。一般资料包括：性别、年龄，糖尿病病程、受教育年限、体质量指数（BMI）、血压等。生化检查包括：糖化血红蛋白（HbA1c）、空腹血糖、C肽、甘油三酯、总胆固醇、低密度脂蛋白胆固醇（LDL-C）、高密度脂蛋白胆固醇（HDL-C）等。

由于出险概率越高，保险人收取保费越高，并提供更少的保险；采取防范措施降低出险概率会使成本增加。整理可得U22＜U11,V22＜V11。

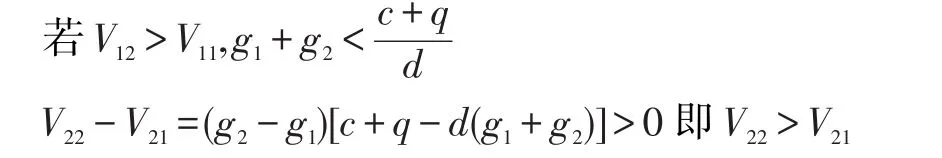
综上可得，V22＞V21，V12＞V11，即在静态博弈中，不采取防范措施是投保人的占优策略，而若投保人选择不防范的策略，保险人的最优反应是收取高保费，因此均衡是（U22，V22）。这是一个典型的囚徒困境的非合作解，帕累托无效，因为如果投保人选择防范措施，而保险人收取低保费，双方状况都能得到改善，但是代表更高福利的（U11，V11）组合并没有成为均衡解。

但是，如果在一个无限重复博弈的结构中，结果就会不一样。假设当事人在任何一个阶段的收益等于其在本阶段所得以及以后阶段博弈产生的收益的贴现值之和。设保险人与投保人的贴现因子均为δ，此时投保人的收益为：

如果保险人采取低保费策略，而投保人采取小心防范的策略，则在以后的博弈中，双方保持合作，此时投保人的收益为：

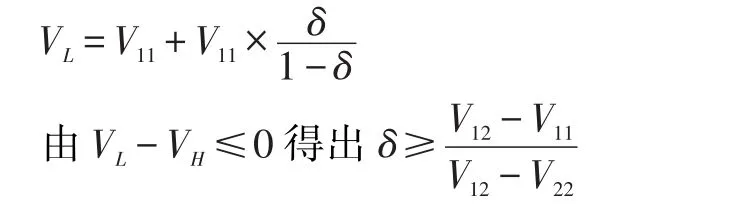
只要贴现因子δ趋于无穷大，即当事人重视未来合作收益，采取防范的策略就是投保人的最优选择，即VL≤VH。如果投保人一直采取合作的策略，保险人也一定会采取合作策略。只要投保人采取了合作策略，保险人没有激励偏离低保费的合作策略。由此可见，在一个重复博弈的结构中，如果当事人足够重视未来收益，道德风险是可以避免的，就有可能达成一个合作的均衡，博弈双方福利均能得到帕累托改善。

（三）传统博弈数学模型的缺陷

通过对保险系统非对称信息博弈模型的分析可以看出，首先，传统的博弈数学模型在假设上采取“完全理性”的分析，这在现实世界中不可能存在，所以，分析结果可能得不到事实的检验。其次，在基于博弈数学模型的建模方法中，模型由一系列方程式组成，而模型的运行就是计算这些方程的过程，不能反映复杂保险系统中Agent之间的交互反应行为，不能形象地模拟出保险系统运行的过程。最后，基于博弈数学方程的模型，要分析的过程是用一组流量变量和水平变量描述的用数学方程组来定义的传统模型，其处理和求解往往需用复杂艰深的理论和技巧，所得结果有时无法进行实证检验。因此，对于复杂保险系统中的传统博弈论这一难题难以全面有效的解决。

四、复杂保险市场系统模型机制

（一）保险系统是一个复杂适应性系统

保险系统作为社会经济系统的子系统，是作为一个整体存在进行发展和演化的。霍兰定义了复杂适应性理论中适应性主体，为了使这些主体能够相互作用、相互影响、相互协同，促进系统的演化与发展，他又提出了对CAS理论都通用的四个特性——聚集、非线性、流及多样性，三个机制——标识、内部模型和积木机制。

1.聚集：保险系统作为一个复杂适应性系统，主体之间的相互作用是保险系统发展的前提条件。包含保险产品、保险人才、保险机构以及保险交易活动在内的各类金融要素资源在一定空间范围内的聚集形成保险聚集。在复杂保险系统的演变过程中，较小的、较低层的个体（如基础保险产品、保险人才）在一定条件下，通过某种特定的聚集形成较大的、较高层次的个体，如基础金融产品通过新的组合变化聚集成更高层次的多元化的保险产品，各种新型的保险产品又吸引了更多的投资者，更多投资者的聚集必然会涌现出更为复杂的保险系统。聚集不是对个体的简单合并，而是更新型更高层次上的个体的出现，原来的个体在更适应自己的生存环境中得到了发展。

2.非线性：保险系统的复杂性特征正是由于保险系统中的个体主体之间的非线性作用构成的。非线性表明保险系统上的某些现象不是个体参与者行为表现的简单加总，仅仅通过观察和研究参与者个体的表现，是不能从总体上认识造成这些现象的原因，而必须作基于整个保险系统的研究，寻找整体性的规律。

3.流：复杂保险系统中存在着各种各样的流，主要有保险信息流和保险资源流。保险信息流和保险资源流存在运行于各种保险主体构成的网络中。保险主体作为节点，是处理者；而保险主体之间可能的相互作用、相互联通方式是流的连接者；保险资源通过保险主体和保险主体作用、连接网络不断地流动。

4.多样性：保险系统多样性通过保险体系多样性、保险机构多样性、保险产品或保险服务品种的多样性、保险行为的多样性、决策规则的多样性、投资者的多样性、保险创新实践的多样性、信息的多样性等多层面、多视角、全方位地呈现。

5.标识机制：复杂适应性系统的聚集导致了系统层次性的出现，但并不是任意的两个主体都可以聚集在一块，只有那些为了完成共同功能的主体之间才存在这种关系，这种共同的功能需要赋予一种可以辨认的形式，这种形式就是复杂适应系统的标识机制。保险系统中的主体通过标识机制的相互作用形成集聚，具有某些共性的主体以同样的标志被识别说明。例如，在保险系统中，投保人可以通过标识机制作用分成低风险投保人、高风险投保人等。

6.内部模型机制：在复杂适应性系统中，主体能够预知某些事情，是因为他们本身存在一种极为复杂的机制——内部模型。内部模型一般分为隐式和显式两类。隐式内部模型在对一些期望的未来状态的隐式预测下，仅指明一种当前的行为。而显式模型用于作为其他选择时进行明显的内部探索，即前瞻过程。如果主体产生的行为对未来的结果能够有效地预知，则主体具有一个有效的内部模型；反之，则具有无效的内部模型。通过进化过程，可以把未来的结果与目前的行为联系起来，从而可以支持有效的内部模型并剔除无效的内部模型。

作为整体的保险系统以及作为其组成部分的每个适应性个体都有基于经验的内部模型，凭借这个模型去感知外界、获取和处理信息、预测未来、采取行动，再总结经验、改进模型等。

7.积木机制：积木是内部模型的生成机制和基本条件。在CAS系统中，基于规则的主体不可能事先准备好一个规则，使他能够适应所遇到的每一种情况。因此，主体通过组合已检验的规则来描述新的情况，那些用于可供组合的活动规则就成为积木。

复杂的保险系统就是由大量的积木块构成的。因此，认识积木、分析积木、改造积木、利用积木是我们剖析保险系统复杂性的切入点，也是保险系统创新的源泉。传统的保险产品通过组合形成更高层次、更复杂的积木块，运用这些基础积木块进行组合又可形成新的保险产品。

保险系统是由保险产品原始提供者（如保险公司）、保险中介机构与投资者以及复杂的外部环境组成的系统。实际市场中的投资者是不具备完全信息的，在这种情况下，投资者对信息存在不同的反应方式，所以预测机制与决策机制也是各异的。在已有的信息下，每个投资者都做出相应的预测与投资决策，最终形成市场价格，相反，市场价格蕴含的信息又对投资者的预测与决策产生影响。这样每个投资者按照市场状态的变化，通过不断学习成功者的经验，形成新的预测规则，并对预测规则进行验证、修改，使投资者的预测规则与市场协同进化。同时在进化过程中，投资者的聚集、分化、对信息的非线性反应方式导致了整个保险系统在宏观层面上呈现复杂性特征。而整个保险系统在宏观层面上的复杂性特征是由在微观层面上各投资者对市场环境进行不断适应调整造就的，保险系统是一个具有复杂自适应性的系统（如图4）。

（二）复杂保险系统的特点

1.复杂保险系统中的主体是具有主动性、适应性的“活”的主体。保险产品、保险人才、保险机构以及保险交易活动等各类金融要素资源之间相互交流，相互“学习”，具有主动性和适应性。

2.复杂保险系统中主体之间、主体与经济环境之间的相互作用和相互影响是市场演化和进化的主要动力。复杂保险系统中的保险产品、保险人才、保险机构以及保险交易活动具有的不同属性，使得他们之间相互作用关系变得更加复杂。同时，这些个体能够聚集成更大的聚集体（金融子系统），这样就使得金融系统的结构多样化。

3.复杂保险系统中主体具有聚集特性，能使简单主体形成具有高度适应性的聚集体，主体的聚集效应隐含着一种“正反馈”机制。复杂保险系统作为一个复杂适应性系统，主体之间的相互作用是金融市场发展的前提条件。

五、保险系统逆向选择模型的动态仿真分析

（一）保险系统逆向模型简介

在逆向模型中，应用基于微观经济主体的建模方法，对模型赋予真实的微观基础。基于Swarm软件平台，构建智能主体的人工生命模型，以模仿复杂保险系统中罗斯切尔德和施蒂格利茨（Rothchild和Stiglitz）保险模型的生成。在施蒂格利茨和阿莫特（Stiglitz和Amott，1988）合作构建的保险系统纯道德风险标准模型中，他们用倒置的因果关系推导出获得高保障的被保险人更容易因为疏于防范而将自己置于更大的风险中。与传统动态分析中应用的数学分析模型相比较，该仿真模型更加直观有效，能够充分地表明系统演化的动力来自于主体之间进行的持续不断的交互改进。整个系统随着主体的适应行为而发生变化，符合客观规律，在一定程度上使得保险系统不对称信息模型更加接近客观现实，为保险系统的健康发展提供了一种新的分析方法。

（二）建模分析过程

假设在逆向模型中，保险公司为代理人Agent，投保人为委托人Agent，假设条件如下：

1.只存在两类风险水平不同的投保人Agent：一类是低风险投保人Agent，一类是高风险投保人Agent。假设不出事收入为revenue0，出事收入为revenue1，风险系数为p。已经参加保险的人标识为insured1，未参加保险的人标识为insured0。

2.所有投保人Agent具有相同的效用函数。

3.保险公司管理成本为零，保险公司对风险持中性态度，市场中所有参与人以利益最大化为出发点。保险公司的属性变量包括保费（premium）、赔偿金额（compensation）、利润（profit）、成本（cost）、参保的投保人的总数量（insured number）、高风险投保人数量（high risk insured number）、低风险投保人数量 （low risk insured number）。

4.保险公司与投保人Agent之间有着信息不对称的现象，也就是说，投保人Agent对于保险公司的保险金和赔偿额非常清楚，但是保险公司并不知道投保人的风险类型。因此只能向每一个投保人收取相同的保险金（因为高、低风险类型的人投保的财产数额相同），在投保人出事的情况下都会支付同样的赔偿额。在上述条件的基础上，构建保险系统逆向模型并进行模拟仿真，具体过程如下：

1.构建一个保险公司模型，对其进行初始化处理，对保险金（premium）和赔偿额（compensation）进行赋值。

2.随机生成投保人Agent，投保人Agent的风险性随机生成。

3.利润（profit）、成本（cost）、参保的投保人总数量（insured number）、高风险投保人数量（high risk insured number）、低风险投保人数量（low risk insured number）这些变量属性的本期值与上一期的值都设置为0。

4.投保人根据效用函数选择是否参加保险：保险前的期望效用函数为expected utility 0=p∗revenue1+（1-p）∗revenue0；参加保险后的期望效用函数为expected utility 1=p∗（revenue1+compensation-premi-um）+（1-p）∗（revenue0-premium）；如果expected utility 1＞expected utility 0，说明参加保险后的效用更大，所以投保人会参加保险。

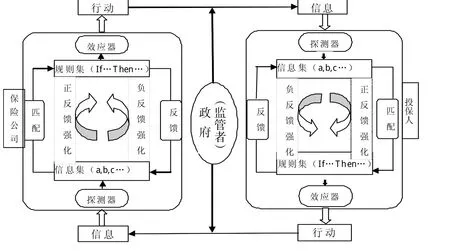
图4：复杂保险系统

5.赔偿：每个参加保险的人在（0，1）区间内产生随机数q，若q＜p，则该投保人Agent会出现事故，保险公司需对投保人赔偿。

6.计算利润：记录参加投保人Agent的数量Insured number和出现事故的投保人Agent的数量compensation number，计算利润profit=insured number∗premium-compensation number∗compensation。

7.主体具有学习能力，可以根据利润的增长来更改保费：在保险公司对某一行为进行确定之后，该行为会在一定程度上影响利润。若利润下降了，保险公司就会认为该行为是“不好”的，所以必须减小该行为发生的概率；若利润上升了，则保险公司就会认为该行为是“好”的，所以必须增加该行为发生的概率。运行程序结果如下（见图5、6、7）：

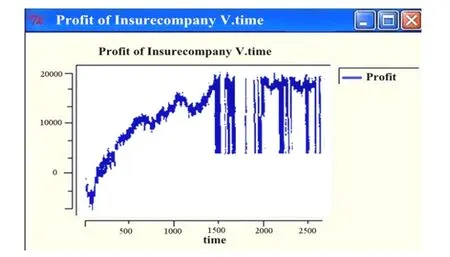
图5：保险公司利润时序图

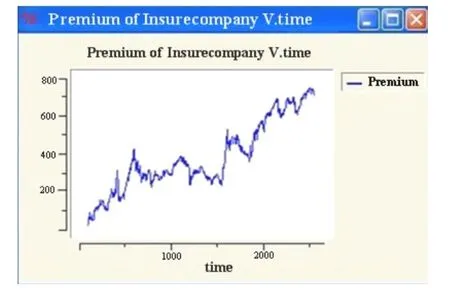
图6：保费时序图

图7：高低风险投保人数时序图

（三）模拟仿真结果分析

借助计算实验金融学的研究方法，结合保险系统微观结构理论和博弈论，遵循“自底向上”的复杂系统建模思路，通过多主体仿真技术构建了复杂保险系统，把交易者定义为具有自适应性的主体（Agent），根据市场环境的变化，调整利率，进而模拟实际市场的演化过程。

研究发现，当程序运行一段时间后保险公司的利润与保费大幅上升，高风险投保人占据主要市场，将低风险投保人“挤出”保险系统。随着保费不断提高，低风险投保人不愿承担过高的保费而退出了保险系统，此时市场上只剩下高保费的高风险投保人。所有的高风险投保人要么都参加保险，要么都不参加保险。对于高风险投保人来说，若投保是有利的，他们就会参加投保，那么保险公司的利润随即会升到一个最高值，此时在受到保费修改策略的影响下，保费会继续上升直到高风险投保人认为保费太高时，才同时退出市场，与此同时参加保险的人数为零，所以在受到保费修改策略的影响下，应该降低保费，直到保费下降到一定水平，高风险投保人重新投保，这样反复下去便出现了上述的运行结果图。

若有关投保人关于风险程度方面的信息是非对称的，则帕累托最优保险合同是不可能达到的。所以，由于信息不对称，低风险投保人会被高风险投保人“挤出”市场，这种逆向选择行为在保险系统中是客观存在的。

六、结论与政策建议

本文用动态仿真的方法实现了对保险系统逆向选择现象的检验。因此，在信息不对称的保险系统中，帕累托最优保险合同是不可能达到的。对于市场参与者的双方而言，信息是不对称、不完全的，彻底消除不对称信息对保险系统的束缚是不可能的，但我们可以采取措施尽可能地减少信息不对称对保险市场产生的不良影响，从而使我国保险系统能够适应市场竞争的要求，健康、持续、有序发展。

首先，通过动态仿真结果可以看出，在信息不对称的保险系统中，低风险投资者将会被高风险投资者“挤出”市场，不利于保险系统的健康运行，因此要解决保险系统信息不对称问题，加大信息披露力度。关于保险系统的信息披露法律制度既是保险监管机构对保险公司进行监管的主要手段之一，也是促进保险系统健康持续发展的客观要求。只有对信息进行充分及时的披露，才能保障投保人公平获取信息，保险监管机构和被监管机构的行为才能接受公众的监督，公众才能主动维护自身利益。市场参与者对保险市场的监督也非常重要，成熟的市场上总有相互对立的利益主体，各种利益主体、各方的分析师和媒体一起形成强大的市场合力，推动了市场透明度的提高。

其次，通过仿真过程可以看出保险系统中仅存在委托人Agent与单一形式的代理人Agent，委托人对代理人的选择单一化，因此完善代理人有利于保险系统的良性发展。在国外，保险市场较为成熟，保险中介市场由保险代理人（代表保险公司）、保险经纪人（代表投保人）以及处于中立的保险公估人组成。而我国的保险营销主要是由个人代理人来完成的，这显然不利于我国保险业的健康持续发展。保险中介机构可以根据所掌握的信息以及相应的专业优势向参与双方提供服务，增加保险运作的透明度，提高公平性，有效降低信息成本，最终推进交易的成功。完善的保险中介制度对于改善保险市场出现的信息不完全、不对称状况具有重要意义，能够在一定程度上防范逆向选择与道德风险的产生。

最后，仿真结论对提高实际保险系统监管工作有一定的借鉴意义。R&S保险模型只是实现了真实决策策略和现实环境中一部分的仿真，并没有加入监管人Agent。监管机构对保险系统中个体的行为进行有效的约束与监管，将会在一定程度上抑制逆向选择与道德风险行为的发生，从而促进了保险系统的健康发展。

[1]Rothchild，M.and J.Stiglitz.1976.Equilibrium in Competitive Insurance Markets[J].Quarterly Journal of Economics，93.

[2]Arnott R J，Stiglitz J E.1988.The Basic Analytics of Moral Hazard.Scandinavian[J].Journal of Economics，90（3）.

[3]刘超，刘丽.系统金融理论研究——兼现代金融理论、行为金融理论、系统金融理论比较[J].南方金融，2011，（12）.

[4]苗东升.系统科学精要[M].北京：中国人民大学出版社，2010.

[5]邓宏钟，谭跃进，多人混合博弈的仿真分析[J].管理科学学报，2002，（4）.

[6]王文举，杨思磊.复杂适应性系统、博弈论及经济动态模拟[J].首都经济贸易大学学报，2002，（5）.

[7]任韬.基于适应性主体的保险市场经济动态模拟研究[J].理论与当代，2009，（12）.

[8]姜璐，谷可.从复杂性研究看非线性科学与系统科学[M].系统科学与工程研究（2版），上海：上海科技教育出版社，2001.

[9]李士勇.非线形科学与复杂性系统[M].哈尔滨：哈尔滨工业大学出版社，2006.

[10]李倩.保险系统中逆向选择模型的仿真检验[J].首都经贸大学学报.2005，（5）.