模型不确定非线性系统的自适应模糊Backstepping预测控制

郑 兰，周卫东，廖成毅，程 华

（1.哈尔滨工程大学自动化学院，150001哈尔滨；2.齐齐哈尔建华机械有限公司，161006黑龙江齐齐哈尔）

模型不确定非线性系统的自适应模糊Backstepping预测控制

郑 兰1，周卫东1，廖成毅1，程 华2

（1.哈尔滨工程大学自动化学院，150001哈尔滨；2.齐齐哈尔建华机械有限公司，161006黑龙江齐齐哈尔）

为解决一类模型不确定严格反馈非线性系统的跟踪控制问题，提出一种使闭环系统稳定且滚动时域性能指标在线最小化的自适应模糊反步预测控制策略.模糊系统用来逼近该设计过程中的未知非线性项，自适应参数直接用来估计最优逼近权值向量范数的平方，从而只有一个自适应参数需要在线调节；同时考虑模糊基函数的性质，所设计的控制律与自适应律均不含模糊基函数项，理论证明该方法设计的控制器保证闭环系统所有信号是半全局有界的，并且跟踪误差收敛于零的某一邻域.该方法所设计的控制器形式简单，计算量小，更易于实际应用，仿真算例验证提出算法的有效性.

模型不确定；滚动时域；模糊自适应控制；反步设计；预测控制

在各类工业系统中，不确定性普遍存在，且有可能使系统性能变差甚至导致系统不稳定.因而，不确定系统的控制器设计成为控制领域研究的热点.由于Backstepping设计方法在处理具有严格反馈形式的不确定系统时所特有的优越性，已成为设计非线性系统控制器的主流工具［1-8］.但反步设计法对可调整的性能指标缺乏“自适应”能力.相反，预测控制在最优控制的框架内可显示地处理系统的控制目标，这使得预测控制无论在理论上还是在实际应用中都取得了令人瞩目的发展.

模型预测控制（model predictive control，MPC），又称为滚动时域控制（receding horizoncontrol，RHC），是处理不确定问题的一种行之有效的方法.它通过在线优化给定的目标函数来设计控制器，现已被广泛应用于各个领域.针对不确定系统的鲁棒预测控制研究目前倍受关注［9-16］.何德峰等［9］采用仿射输入定义预测控制的控制律，研究了一类模型不确定非线性系统的H∞鲁棒预测控制；平续斌等［10］基于辅助优化方法研究了一类具有多胞不确定性和有界噪声系统的动态输出反馈鲁棒模型预测控制，并将闭环系统的稳定性进行了扩展；刘晓华等［11］针对一类同时具有状态和输入时滞的不确定广义系统通过近似求解无穷时域二次性能指标优化问题，提出了鲁棒预测控制器的设计方法；苏成利等［12］在文献［11］的基础上，针对一类同时存在多重状态和输入时滞且具有非线性扰动的不确定系统研究了其鲁棒预测控制器的设计方法；黄鹤等［13］针对具有有界扰动的多胞不确定系统着重研究了采用混合H2／H∞指标的鲁棒预测控制算法的设计及其可行性、稳定性以及在线计算量的分析；史冬琳等［14］针对有扰动的受限非线性系统，基于仿射控制输入方法提出了一种反馈控制策略，且给出了扰动上界的求解方法；郑鹏远等［15］基于控制不变集方法研究了一类具有结构不确定性时滞系统的闭环鲁棒预测控制算法，增加了控制设计的自由度；杨国诗等［16］将预测控制与构造性控制结合研究了基于反步设计的构造性非线性预测控制算法；张利宾［17］等针对多卫星处置阶段非线性姿态控制算法进行了研究，基于反馈线性化理论研究了非线性预测控制算法设计，并对系统的鲁棒性进行了分析.该控制算法具有良好的抗扰性，快速性，稳定性和鲁棒性；杨青等［18］将预测控制与反步设计方法相结合，针对模型不确定的非线性系统设计了一种预测控制器，该方法比传统的预测控制算法更容易使闭环系统稳定，且具有良好的动态特性.但此方法是在假设系统的不确定性是有界且为已知的有界光滑函数的前提下研究的，使用范围很有限.因此，针对更一般的系统设计相应的控制器是需要进一步解决的问题.

本文在文献［18］的基础上直接针对一类模型不确定的严格反馈非线性系统设计基于反步法的自适应模糊控制器.通过每一步对Lyapunov函数的构造以及对模糊逻辑系统的使用，最终得到实际的控制律和自适应律，与此同时系统的不确定性也得以解决.与以往所设计的控制器相比，本文所设计的控制器结构简单，并且包含更少的自适应参数（只有一个），从而降低了计算量，减少了计算时间.仿真结果验证了该算法的有效性.

1 问题描述

考虑如下一类单输入单输出非线性系统

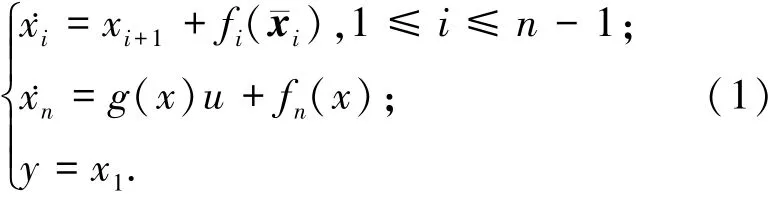
式中：ˉχi＝［χ1，χ2，…，χi］T，（i＝1，2，…，n-1）；χ＝［χ1，χ2，…，χn］T∈Rn和u∈Rn分别是系统状态向量和控制输入；y∈R为系统输出；fi（·），g（·）和fn（·）为未知光滑非线性函数，i＝1，2，…，n-1．控制目标是设计一个稳定的自适应控制器，使系统式（1）所有的信号半全局有界．为此，作如下假设：

假设1 存在正常数gr和ˉg≥g＞0使函数g（χ）满足0＜g≤｜g（χ）｜≤ˉg且｜.g（χ）｜≤gr．这里，不妨设g（χ）≥g＞0．

假设2 yd（t）及其一阶导数.yd（t）是已知光滑有界函数．

在自适应模糊控制设计中，首先引入误差向量

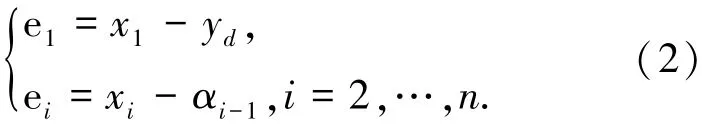
式中：yd表示期望输出，＾αi是期望虚拟控制信号，将在第i步中给出．

考虑系统式（1）中存在的未知非线性，将采用模糊系统来进行逼近.根据万能逼近定理，可以把模糊系统写为如下形式：

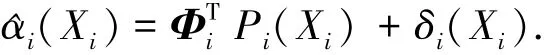
式中：Φi为最优权向量，Pi（Xi）为模糊基函数，δi（Xi）为逼近误差，且｜δi（Xi）｜≤εi，εi为某一正常数．模糊基函数Pi（Xi）满足0＜（Xi）Pi（Xi）≤1．

定义

在控制器设计步骤中，＾θ为θ的估计，估计误差˜θ为˜θ＝θ-＾θ．

自适应Backstepping控制算法中虚拟控制量以及自适应律设计如下：

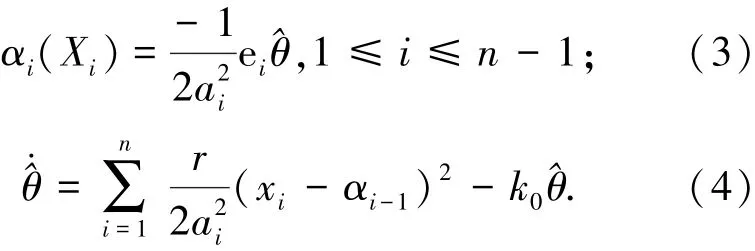
式中k0，r，ai（i＝1，2，…，n）为设计的正常数，实际控制律u＝αn，即

2 主要结论

2.1 控制器设计

控制器设计分为n步，在每一步中将设计虚拟控制律αi，i＝1，2，…，n．最后，在第n步时将会得到系统的控制律u．

步骤1 考虑如下的Lyapunov候选函数

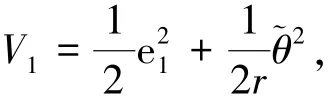
由式（1）、（2）可知

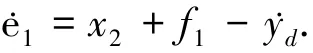
对V1求导有

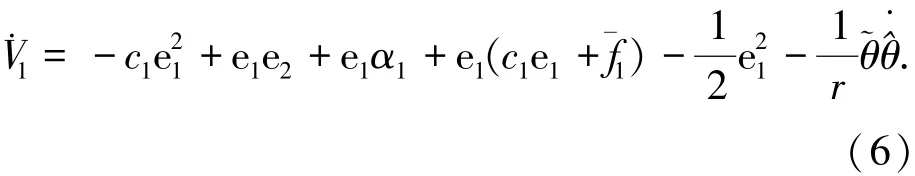
式中c1为常数，

因为＾α1为未知函数，用模糊逻辑系统来逼近＾α1，

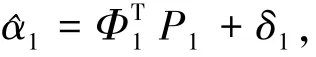
式中｜δ1｜≤ε，ε1是一个正常数．

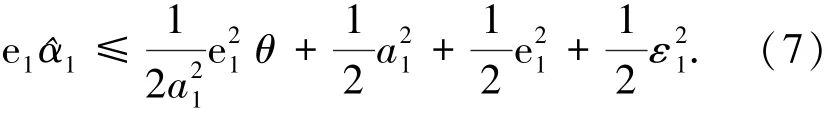
将式（5）、（12）代入式（10），整理可得：

步骤2 选取如下的Lyapunov候选函数

对V2求导得

式中：c2为一个常数，＾α2＝c2e2＋ˉf2，

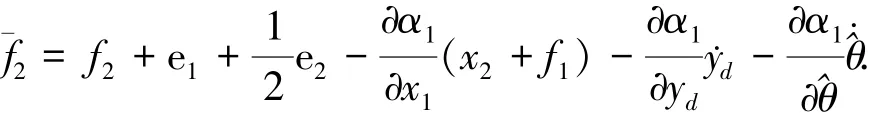
利用模糊系统和虚拟控制α2可得

步骤k （3≤k≤n-1），利用类似的推导过程并选择Lyapunov候选函数为

利用模糊系统和虚拟控制αk同理可推出

步骤n 这一步将得到控制u，根据式（1）、（2）可得

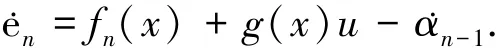
式中：c′n为一个常数，

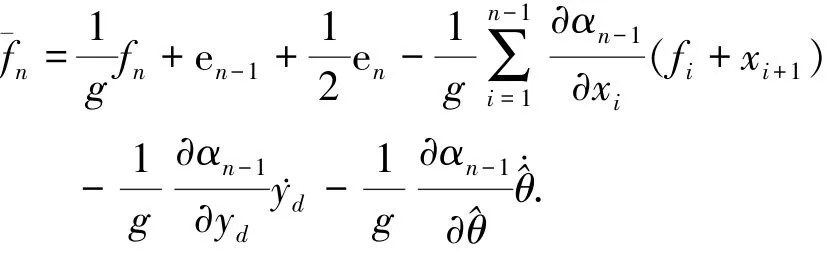
采用模糊系统来逼近未知函数＾αn，可得

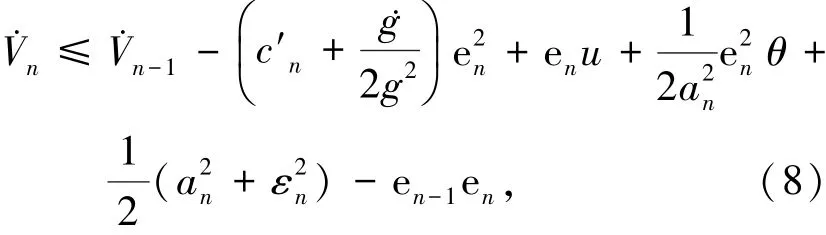
由假设1可得

通过选择适当的c′n使得

将式（5）、（9）代入式（8），.Vn可进一步表示为

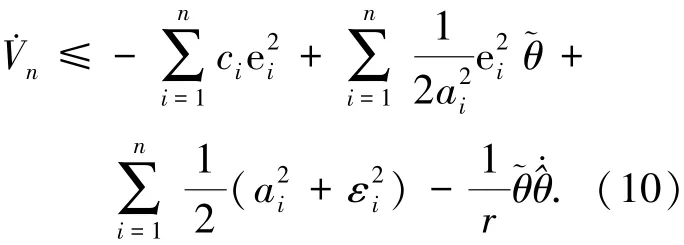
从步骤1到步骤n的设计过程来看，控制律u的设计清晰明了，对比文献［9-10］等，此文的关键之处在于采用了一种新的Lyapunov函数，自适应律仅包含一个参数θ．与文献［18］所设计的控制器相比，本文设计的控制器结构简单，降低了计算量，减少了计算时间.

2.2 稳定性分析

为了分析闭环系统的稳定性，选取Lyapunov候选函数为V＝Vn．由式（4）、（10）可得

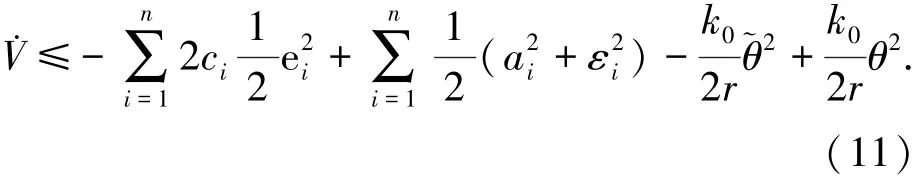
设a0＝min｛2ci，k0，i＝1，2，…，n｝，

由式（11）得.V（t）＋a0V（t）≤b0，则

in）和˜θ都是有界的．又因为θ是一个常量，则＾θ是有界的，所以αi也是有界的．由此得出χi是有界的．证明闭环系统所有信号是有界的．ci，r，ai和k0是设计的参数，并且θ，g和ˉg是常数．对任意给定的ε＞0，首先设计参数ci和k0，选择ai，εi和ρ充分小且r充分大，可得b0／a0≤ε2／2．另外，由式（12）得

3 控制器参数在线优化

利用在线滚动优化确定控制器参数，提出一种非线性预测控制算法.在传统的Backstepping设计中控制器参数c1，c2，…，c′n为时变的正实数变量，在滚动优化过程中，在线调整参数c1，c2，…，c′n使得预测控制的目标函数最小．

为适应在线计算机计算的需要，采用差分的方法把系统式（1）、（3）和（5）离散化，采样时间为T：

考虑取目标函数为

1）RΔu（k＋i-1）］＋eT（k＋P）Se（k＋P）．式中：Δu为输入量的变化量，Q，S为正定矩阵，R为正实数，P为预测时域.基于Backstepping设计思想的非线性预测控制算法为

通过在线求解有约束非线性规划的方法，得到使目标函数最优的控制器参数矩阵C，得到所设计的预测控制器.采用序列二次规划的方法求解［19-20］.

4 仿真研究

考虑如下三阶非线性系统：

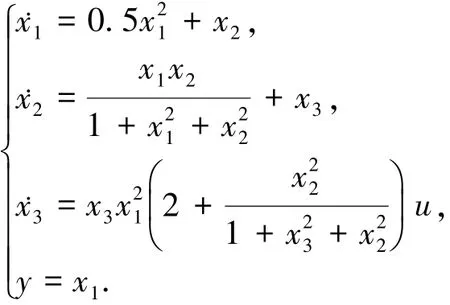
定义yd＝sin 2t＋cos t，控制律与自适应律为

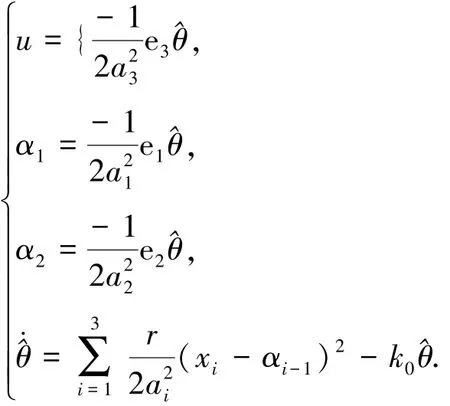
由图1～2可以看出系统输出能跟踪给定的期望信号，跟踪误差收敛于零的某一邻域.图3表示控制输入，由图可知控制输入有界.图4为系统性能指标，可知所设计的控制器可使得性能指标在线最小化.

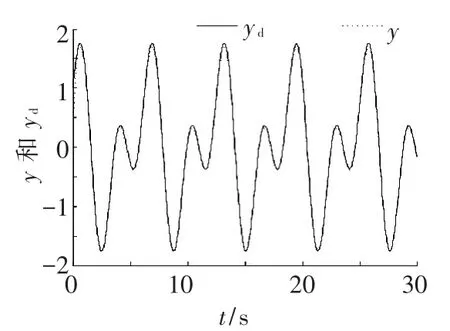
图1 系统输出与期望信号曲线轨迹

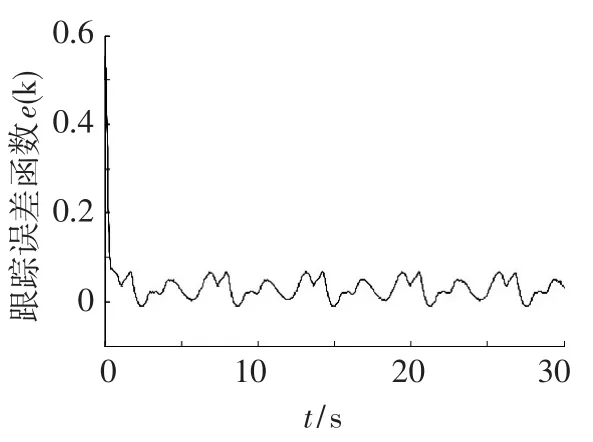
图2 跟踪误差曲线

图3 控制输入曲线

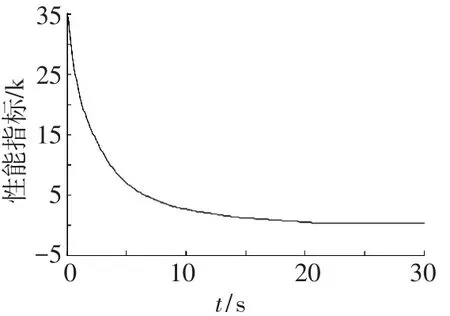
图4 性能指标曲线

5 结 语

针对模型的不确定性，本文研究了一类严格反馈非线性系统的自适应模糊反步预测控制算法.反步设计方法与模糊系统的引入解决了模型的不确定性，降低控制器的设计难度.考虑万能逼近特性和模糊基函数的性质，设计的控制器结构简单，且有效降低预测控制在线优化的计算量.通过仿真验证了所提出控制器设计方法的有效性.

［1］KANELLAKOPOULOS I，KOKOTOVIC P V，MORS E A S.Systematic design of adaptive controllers for feedback linearizable systems［J］.IEEE Transactions on Automatic Control，1991，36（11）：1241-1253.

［2］ZHANG Tao，GE S S，HANG C C.Adaptive neural network control for strictfeedback nonlinear systems using backstepping design［J］.Automatica，2000，36（12）：1835-1814.

［3］YANG Yansheng，ZHOU Changjiu，REN Jusheng. Model reference adaptive robust fuzzy control for ship steering autopilot with uncertain nonlinear systems［J］. Applied Soft Computing，2003，3：305-316.

［4］YANG Yansheng，FENG Gang，REN Junsheng.A combined backsteppingandsmall⁃gainapproachto robust adaptive fuzzy control for strict⁃feedback nonlinear systems［J］.IEEE Transactions on Systems，Man，and Cybernetics⁃PartA：SystemsandHumans，2004，34（3）：406-420.

［5］ZHOU Jing，WEN Changyun，WANG Wei.Adaptive backstepping control of uncertain systems with unknown input time⁃delay［J］.Automatica，2009，45（6）：1415-1422.

［6］WEN Changyun，ZHOU Jing，WANG Wei.Decentralized adaptivebacksteppingstabilizationofinterconnected systems with dynamic input and output interactions［J］. Automatica，2009，45（1）：55-67.

［7］CHEN Bing，LIU Xiaoping，LIU Kefu，et al.Direct adaptivefuzzycontrolofnonlinearstrict⁃feedback systems［J］.Automatica，2009，45：1530-1535.

［8］文杰.非仿射非线性不确定系统的自适应模糊控制研究及应用［D］.南京：南京航空航天大学，2011.

［9］何德峰，季海波，郑涛.持续有界扰动下的非线性H∞鲁棒预测控制［J］.自动化学报，2008，34（2）：215-219.

［10］平续斌，丁宝苍，韩崇昭.动态输出反馈鲁棒模型预测控制［J］.自动化学报，2012，38（1）：31-37.

［11］刘晓华，王利杰.带有状态和输入时滞的不确定广义系统的鲁棒预测控制［J］.控制理论与应用，2010，27（4）：527-532.

［12］黄鹤.混合H2／H∞指标鲁棒模型预测控制器的设计［D］.上海：上海交通大学，2011.

［13］苏成利，赵家程，李平.一类具有非线性扰动的多重时滞不确定系统的鲁棒预测控制［J］.自动化学报，2013，39（5）：644-649.

［14］SHI Donglin，MAO Zhizhong.Input⁃to⁃state stabilizing MPC for constrained nonlinear system with persistent disturbance［C］／／Proceedings of the Chinese Control and Decision Conference（CCDC），Mianyang：IEEE，2011，1126-1129.

［15］ZHENG Pengyuan，XI Yugeng，LI Dewei.Closed⁃loop robust model predictive control for time⁃delay systems with structured uncertainties［J］.Control Theory＆Applications，2013，30（6）：683-692.

［16］杨国诗，何德峰.基于反步设计的构造性非线性预测控制算法［J］.信息与控制，2011，40（3）：314-317.

［17］ZHANG Libin，CUI Naigang，PU Jialun.Research on nonlinear attitude control algorithm for upper stage during multi⁃satellite disposing［J］.Journal of Harbin Institute of Technology（New Series），2011，18（5）：14-18.

［18］杨青，李树荣.基于Backstepping设计的不确定非线性系统的预测控制［J］.控制理论与应用，2007，24（4）：525-529.

［19］袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2001.

［20］赵敏，李少远.基于信赖域二次规划的非线性模型预测控制优化算法［J］.控制理论与应用，2009， 26（6）：634-640.

（编辑 苗秀芝）

Adaptive fuzzy backstepping predictive control for a class for nonlinear systems with model uncertainty

ZHENG Lan1，ZHOU Weidong1，LIAO Chengyi1，CHENG Hua2
（1.College of Automation，Harbin Engineering University，150001 Harbin，China；2.Qiqihaer jianhua machinery co.，LTD，161006 Qiqihaer，Heilongjiang，China）

To overcome the tracking control problem for a class of strict⁃feedback nonlinear system with model uncertain，an adaptive fuzzy backstepping predication control algorithm which can make the closed⁃loop system stable and minimize the receding horizon guaranteed cost on⁃line is proposed.Fuzzy logic systems are employed to approximate the unknown term in the design process.As the adaptive parameter are directly used to estimate the norm of the optimal approximation weight vector，only one parameter need to be tuned on⁃line.Considering the property of the fuzzy basis function，the designed control laws and adaptive laws do not contain the fuzzy basis function term.Theoretically，it is proved that the using the constructed controller can guarantee that all signals in closed⁃loop are semi⁃globally uniformly ultimately bounded，and the tracking error convergence to a small neighborhood of the origin.As the form of the controller designed in this way is simplicity and the computation is small，this control strategy is easily realized in practice.Finally，the simulation results demonstrate the feasibility of the proposed scheme.

model uncertain；receding horizon；fuzzy adaptive control；backstepping design；prediction control

TP273

：A

：0367-6234（2014）11-0107-05

2013-10-09.

国家自然科学基金（61102107；61374208）.

郑 兰（1982—），女，博士研究生；周卫东（1966—），男，教授，博士生导师.

郑 兰，zhenglan000＠163.com.