深圳市人口与医疗需求预测*

朱家明,张月茹,郭 溪,郑 路

(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)

深圳市人口与医疗需求预测*

朱家明,张月茹,郭 溪,郑 路

(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)

针对深圳市人口与医疗需求，以人口的变化与结构特征为切入点，综合分析了2002-2011年深圳市及各区人口基本情况、2002年以来深圳市床位需求状况以及某些疾病的就医情况的数据资料，建立了人口增长和Leslie预测以及马尔科夫预测等模型，得出深圳市未来十年人口与医疗需求变化的预测.

修正Frisch法;Leslie模型;组合预测;马尔科夫预测

深圳作为中国改革开放的前沿和工业化的先锋城市，高速发展引发各地劳动力的大量流入.随着时间推移，深圳人口老龄化和产业结构的变化都可能影响深圳市未来的医疗需求.现据已有数据，分析深圳近十年人口变化特征，预测其发展趋势，以此为基础预测未来全市和各区医疗床位需求.

1 人口增长模型及未来十年深圳市人口的预测

1.1 数据的来源与处理

对2002-2012年深圳市常住人口与非常住人口数据整理并分别求和得各年总人口(如表1).

将2002年作初始时刻即t=0 ，则2011年为终时刻9(以年为单位).运用Matlab软件作散点图进行线性拟合，如图1.

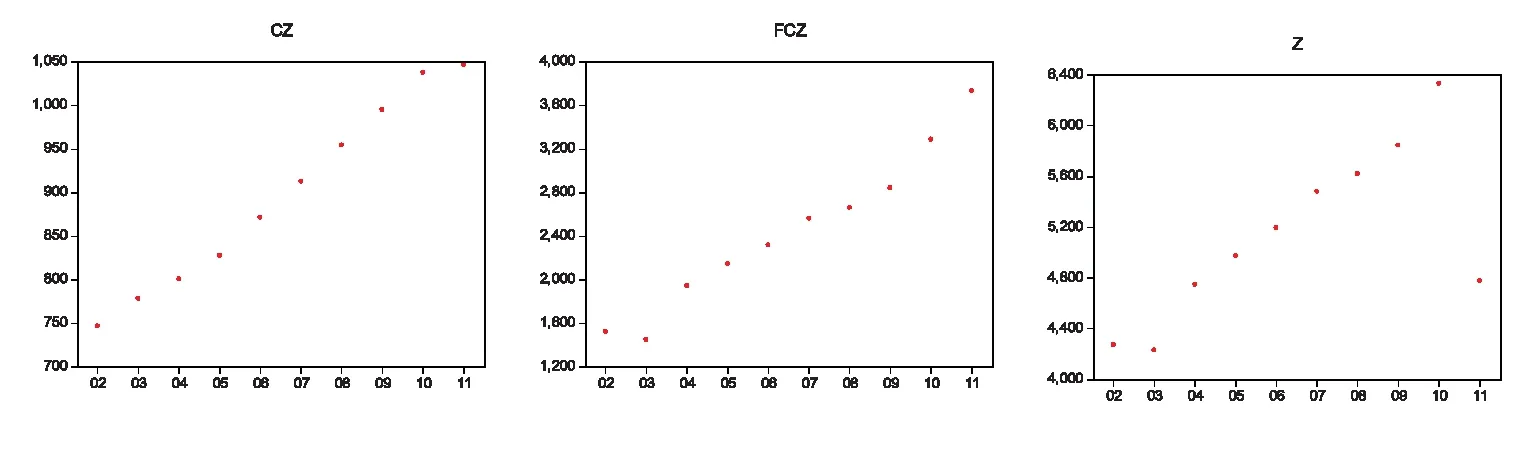
图1 2002-2011年常住人口、非常住人口及总人口散点图

三类人口均呈现线性变化趋势，用Eviews6进行线性拟合：

ycz=735.9549+35.7909t,

yrcz=1381.024+236.4944t,

Yz=4411.488+163.5944t

1.2 未来十年深圳市总人口预测

根据以上三个模型得到三类人口的预测值(如表2).

表1 2002-2011年深圳市常住人口、非常住人口、总人口(单位：万人)

表2 2012-2021年深圳市常住人口、非常住人口、总人口预测(单位：万人)

1.3Leslie人口模型及未来十年深圳市各年龄阶段人口百分比的预测

这里采用Leslie人口模型[1]，按三步对深圳市各年龄阶段人口百分比进行研究.

(1)计算2010年深圳市各年龄段妇女人数的分布向量ci(0),i=0,1,…,20.

设在时间段t第i年龄组的人口数为ci(t) ，2010年深圳女性人数占总人口的比例是p(且假设各年龄段妇女所占比例均为p)，则第i年龄阶段的妇女人数为ci(0)=p·ci.

(2)计算在第i(i=0,1,…,20) 年龄段的每个女性平均生育女儿的生育率bi(i=0,1,…,20).

根据各年龄段妇女(15-49岁)的生育率(i<4 或i>10 时均为0)，可以估算出2010年处在第i年龄段深圳市妇女生育的小孩数Hi，那么Hi=bici(0) .经查阅，2011年深圳市男女出生人口性别比c(女100计)，求出2011年处在第i(i=4,5,…,10)年龄段的每个女性平均生育女儿的人数：

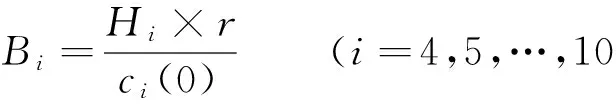
(3)计算第i年龄段的女性总存活率di(i=0,1,…,20).

记第i年龄段的女性死亡率为di，则总存活率为si=1-di.根据Leslie矩阵，再推算出各年龄阶段人口占总人口的比重，如表3.

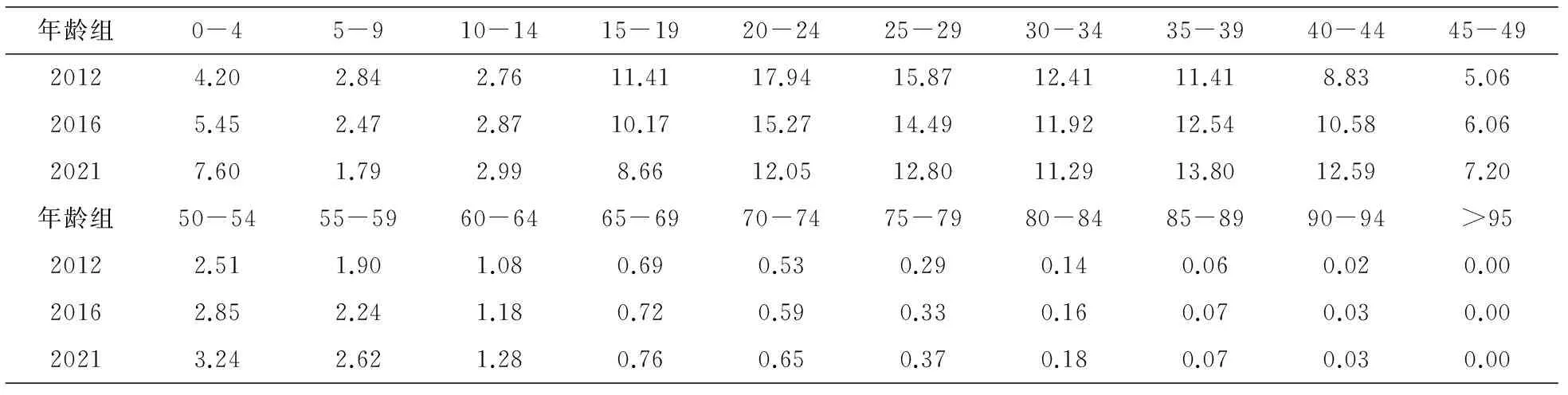
表3 各年龄阶段人口占总人口的比重(单位：%)

分析可知，该市人口年龄结构在2012→2016→2021年的变化过程中中老年人的比重呈明显的上升趋势，即说明深圳市人口老龄化现象开始出现.

2 对深圳市未来十年床位需求状况进行预测

2.1 模型的建立

(1)模型Ⅰ——-多元线性回归模型

首先，整理数据.得到2001-2011年病床需求量Q(百张)、常住人口数量X1(万人)、非常住人口X2(万人)、性别比X3和老龄人口所占比重X4，如表4.其次，进行相关分析.运用Eviews6.0进行最小二乘估计：

2.9635X3+244.0582X4

DW=1.8496，F=415.23

经检验回归方程显著.采用修正Frisch法[2]检验和处理多重共线性，得到回归方程：

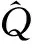
DW=1.8496，F=563.23

虽然解释变量间仍会存在线性关系，但多重共线性并没有造成不利后果，所以该模型是较好的床位需求方程.于是预测出床位需求量，如表5 .

表4 估计深圳市床位需求量的数据

表5 2011-2020年深圳市床位需求的多元线性回归预测(单位：张)

(2)模型Ⅱ——灰色预测模型

①灰色模型 的建立：

其中a,u为待估参数，分别称为发展灰数和内生控制灰数.

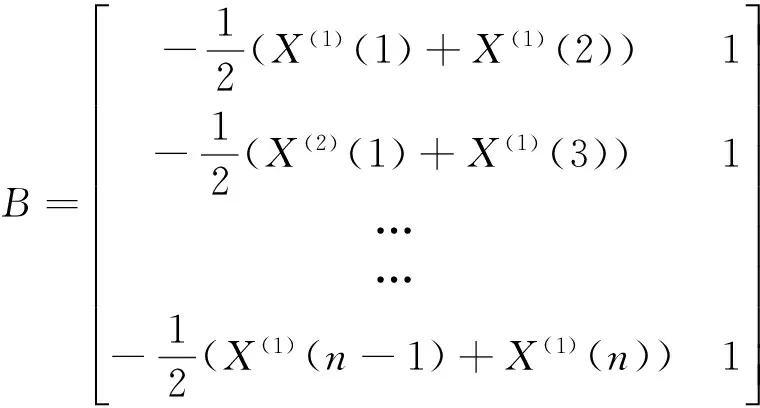
YN=(X(0)(2),X(0)(3)，…,X(0)(N))T.带入微分方程并解该方程，得到GM(1,1)预测模型:

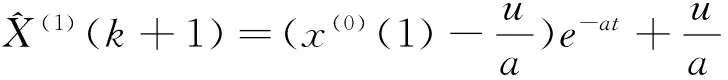
②带入具体数据，用Matlab7编程求解得到预测方程：

x(1)(k+1)=172466.5058e0.072144t-161307.5058

那么2011-2021年的床位需求量如表6所示.

表6 2011-2020年深圳市床位需求量的灰色预测(单位：张)

(3)模型Ⅲ——时间序列模型

借助Excel软件，作散点图建立时间序列模型并预测2012-2020年的床位需求量，如表7所示

表7 2011-2020年深圳市床位需求量的时间序列预测(单位：张)

(4)模型Ⅳ——组合预测模型

选取深圳市床位需求量的历史数据序列(2002-2011年)，将三种模型的预测结果与实际值进行比较并计算残差平方和，如表8所示.

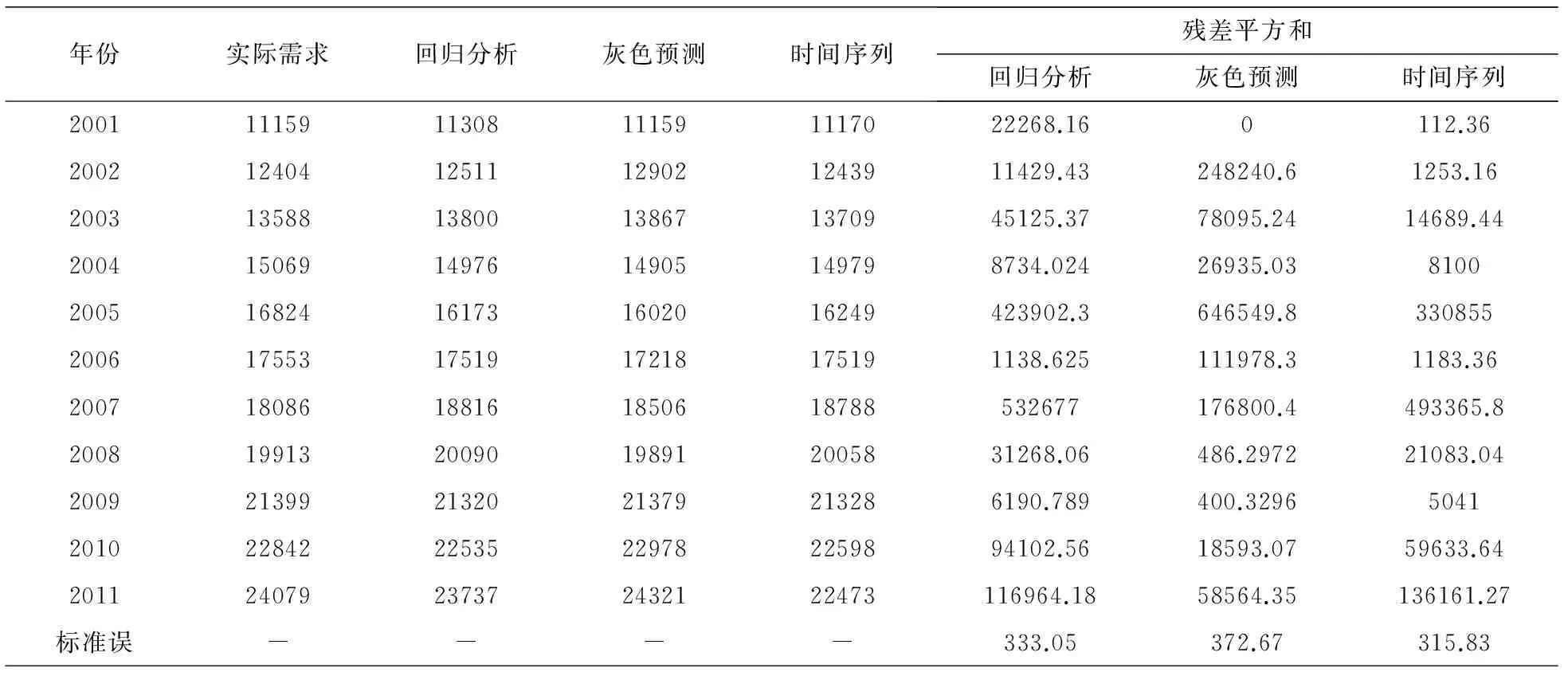
表8 三种预测模型的结果与实际值进行比较

采用拟合优度法对三种预测方法求其权重，取

式中SeI-第i个预测模型标准误差.

表9 2012-2021年深圳市床位需求量(单位：张)

2.2 建立床位需求影响度模型，预测未来十年深圳市各区医疗床位需求

根据2002-2010年深圳市各区人口占总人口比重(%)，宝安区、龙岗区、南山区、罗湖区、福田区和盐田区六个行政区每年的人口比重都是已知的.借助统计软件，对2002-2010年各区的人口的比重进行分析与预测，在此基础上预测两个新区的人口比重.假设深圳各区的医疗床位需求与其占全市人口的比重呈正比，易得出未来十年深圳市各区的床位需求，结果如表10所示.

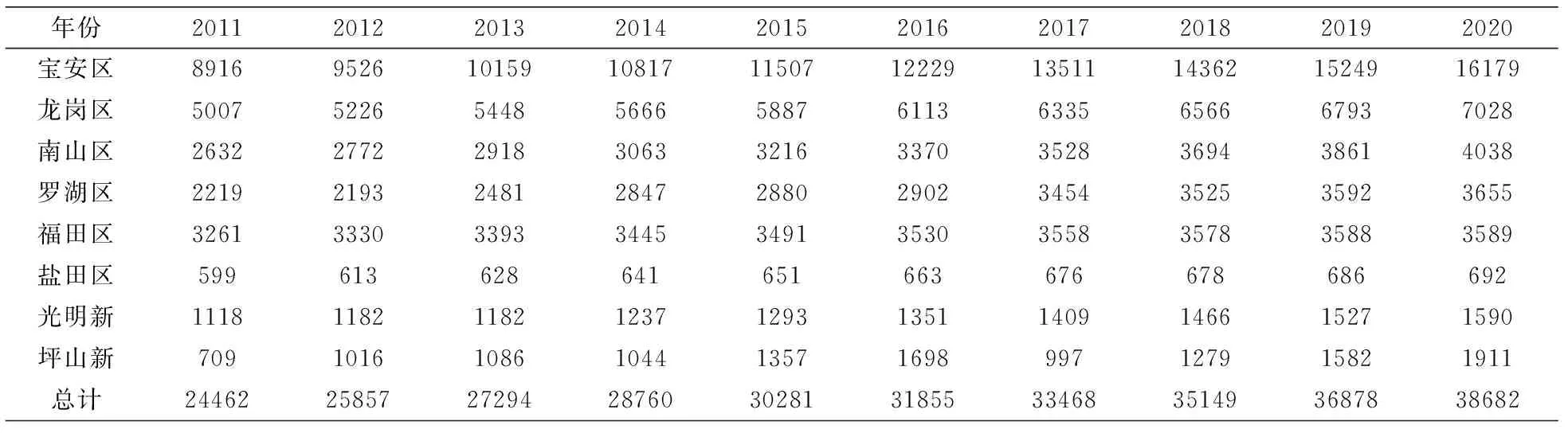
表10 未来十年深圳市各区的床位需求(单位：张)

2.3 床位需求预测

根据深圳市人口的年龄结构和患病情况及收集到的数据[3]，本文选择了小儿肺炎、剖腹产以及心肌梗塞三种疾病，以及综合医院、专科医院(或中医院)和妇幼保健站三种医疗机构.

(1)预测小儿肺炎在不同类型的医疗机构就医的床位需求

小儿肺炎的主要发病人群是在0-14岁，其中0-4岁的发病率为6%，4-9岁的发病率为2%，10-14岁的发病率为0.8%.据已预测出的深圳市年龄结构的人口情况，计算出未来十年小儿肺炎的发病总人数，进而得到病人数与床位数之间的关系可预测出床位的需求量.

由已预测的未来十年常住人口数和人口年龄构成得到小儿肺炎的未来十年患者数，结果如表11所示.第i类医疗机构床位的需求量Qi可以近似看作第i类医疗机构平均每天住院人数ni与平均住院日di的乘积，可表示为Qi=ni×di，其中ni=Ni/365，Ni为第i类医疗机构入院的总患者数目.代入数据可以求解出2011-2020年不同医疗机构对小儿肺炎的床位需求量，如表12所示.

表11 2011-2020年深圳市小儿肺炎不同年龄阶段的患者数目(单位：人)

表12 2011-2020年深圳市小儿肺炎在不同医疗机构的床位需求量(单位：张)

(2)预测剖宫产在不同类型的医疗机构就医的床位需求

由于剖宫产病床需求量与妇女数量有很大的关系，现把妇女的生育年龄定在15-49岁之间，经查阅2010年深圳市剖宫产的总病例数目为48558例，2010年性别比为118.2316，那么15-49岁的女性人数为3925709人，从而得到15-49岁的妇女中剖宫产的人口数量，如表13所示.

由平均每名产妇在综合医院、专科或中医院、妇幼保健院的住院天数分别为7.09天、6.85天、6.92天，则容易得到2011-2020年剖宫产在不同医疗机构的床位需求量，如表14所示.

表13 2011-2020年深圳市15-49岁的妇女中剖宫产的人口数(单位：人)

表14 2011-2020年剖宫产对不同医疗机构床位需求量(单位：张)

2.4 建立马尔科夫预测模型，预测老年心肌梗塞在不同类型的医疗机构就医的床位需求

(1)预测老年心肌梗塞未来十年的患病人数

根据前面计算出的未来十年深圳市各年龄阶段人口总数、人口性别比以及相应的发病率，可以对未来十年深圳市老年心肌梗塞人数进行预测，结果如表15所示.

(2)老年心肌梗塞在不同医疗机构就医的床位需求

老年心肌梗塞患病者在不同医疗机构(综合医院、专科医院)就医可以分成两个状态：E1(在综合医院就医)、E2(在专科医院就医).状态转移概率为pij=p(Ei→Ej) ，pij只与Ei与Ej有关(无后效性)，每个Ei的转移概率之和为1.一步转移概率矩阵如下：

根据2010年老年心肌梗塞患病者在不同医院就医床位所占比重：73.8%、26.2%，得到即初始概率矩阵为S(0)=[0.738 0.262] .

假定转移步数n足够大，根据状态概率逐渐收敛于某一定植求解稳定状态有S(n)=S(n-1)，即n期的状态概率与(n-1)期的状态概率相等[4]，且

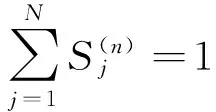
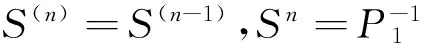
那么综合医院占医疗机构比重为62.5%，专科医院占医疗机构比重为37.5%.根据未来十年每年各医疗机构所接受的老年心肌梗塞的就诊人数，同理可得各个医疗机构的床位需求，如表16所示.

表15 深圳市老年心肌梗塞人数(单位：人)

表16 心肌梗塞患病对各个医疗机构的床位需求(单位：张)

3 结论

预测深圳未来十年的床位需求时，在多元回归、时间序列、灰色预测模型的基础上建立组合模型，使预测的结果更具合理性；充分考虑到不同年龄阶段的个体具有不同的生育能力和死亡率，建立了Leslie模型、年龄结构的离散模型，并通过合理假设在时间跨度不大的前提下，对人口数量进行了预测；根据未来十年深圳市年龄结构、性别比以及总人口情况，预测出小儿肺炎、剖宫产和心肌梗塞所对应的入院人数，根据2010年深圳市单一病种的情况，并建立马尔科夫模型，进而预测出3种常见疾病患者对三种不同的医疗机构相应的床位需求量.不过，由于假设生育率与死亡率不随时段的变迁这一理想的状态下，但出生率及死亡率会随时间的变化而有所改变，本模型没有建立生育率与死亡率随时间变化的动态模型，因而存在一定的误差.

[1]于学军.中国进入“后人口转变”时期[J].中国人口科学,2000(2).

[2]张晓峒.计量经济学基础[M].天津:南开大学出版社,2007.

[3]深圳市卫生和人口计划生育委员会http://www.szhpfpc.gov.cn.

[4]王国维.预测与决策[M].北京:中国财政经济大学出版社,2006.

(责任编辑:王宏志)

2013-09-26

朱家明(1973-),安徽省泗县人,硕士,副教授.

国家自然科学项目(61305070);国家级大学生创新创业训练计划项目(201310378056)

O21；R

A

1008-7974(2014)01-0021-05