基于海西经济区的全要素生产率研究及其实证分析

许贵福

（福建船政交通职业学院 公共教学部，福建 福州 350007）

一、引言

对于全要素生产率 （Total Factor Productivity，TFP）的研究最早开始于丁伯根 （1942）和索洛（1985），Fare（1985,1989,1994）以及 Coelli（1996）研究了全要素生产率变动的测量方法,通过经验分析得出了较好的研究结论。

我国对全要素生产率研究的文献很多，归纳总结主要包括三个方面：（1）根据某些区域的历史数据，运用模型对该区域的全要素生产率进行定量测算，并分析其在此阶段时间的变化特征；（2）根据模型回归的结果，定性地分析全要素生产率对经济增长的影响；（3）阐述一些影响全要素生产率的因素。

改革开放后，中国经济的全要素生产率得到了显著提高.对全要素生产率的研究一直是我国学者研究的热点课题.易纲、樊纲、李岩（2003）指出新兴经济在估算TFP所面临的问题[1].张军、施少华（2003）计算了我国近几年TFP的波动[2]，结果表明，在1952年到1978年改革开放以前，我国TFP具有明显的波动性，改革开放以后，TFP表现较为稳定，有明显的提高。颜鹏飞、王兵（2004）研究Malmquist生产率指数和技术进步[3]，技术效率与技术效率的人力资本机制因素和生产率增长之间关系，得出技术效率、人力资本和制度因素均是影响我国全要素增长的主要因素.郭庆旺、贾俊雪（2005）采取我国1979年—2004年各年的经济生产总值（GDP）[4-5]，研究经济增长与TFP之间的因果关系.即在此期间我国经济增长模式为一个典型的输入式增长模式，TFP增长率低下，技术进步、产能利用率不高和资源的配置不合理影响着经济的增长。章祥荪、贵斌威（2008）使用DEA Malmquist指数方法研究了我国1979-2005年TFP变化情况[6]，也得出了相似的结论。叶德磊、邓金鹏（2009）利用面板模型研究了我国东、中、西三地区的TFP[7]，得出三地区全要素生产率有呈现日益扩大的趋势.邓利方、余甫功（2006）利用面板数据的Malmquist DEA方法对广东TFP进行测算与分析[8]。本文选取Malmquist TFP指数方法测算海西经济区20个城市1995-2012年的面板数据进行实证分析[9]，研究海西经济区TFP对经济增长的影响。

二、研究方法、模型及投入产出设计

（一）研究方法

在研究全要素生产率（TFP）中，目前常用的方法有三种：增长核算法、生产函数法、随机前沿分析法以及数据包络分析法（DEA）。

增长核算法主要是把经济增长简单的分解为两部分，一是全要素生产率的增长，二是投入的增长，运用相关数量模型得出其在经济增长率中的贡献度分别是多少，得出投入增长和全要素生产率的增长对经济增长的影响情况。随机前沿分析法对全要素生产率进一步的分解，减少了测算的误差，但是该方法需要了解生产函数的具体形式。数据包络分析法又简称Malmquist指数方法，该方法的优点就是对价格信息不作具体要求，运用相关的投入和产出数据，就进行测算，因此很好的弥补了其他方法对相关价值和价格数据的要求。数据包络分析法和其它几种方法相比较，最大的优点是可以对指数进行分解，并且不需要通过假设任何具体分布函数来获得前沿函数。1953年Malmquist最早提出Malmquist TFP指数方法[10]，1982年Cavesetal首次运用该方法测算生产率指数变化[11]。该方法在测算全要素生产率变化的优点主要有：一是弥补了在研究生产率指数方面对相关价格信息不全的缺陷；二是把生产要素分解为生产效率变动和技术进步变动，进而计算技术和效率的变化情况。

对于一些生产要素来说，相关价格信息无法统计，其数据较难获得，但相关投入和产出的数据较易获得。因此，本文使用基于数据包络分析 （DEA）的Malmquist生产率指数方法，测算海西经济区1995-2012年的全要素生产率（TFP）的变化。

（二）研究模型

从 t时期到 t+1时期，TFP增长率测度的Malmquist指数可以表示成：

上式中，xti=（Kit,Lit）＇表示第 i个地区第t时期包括劳动（L）和资本（K）的投入向量；用yti=（Yit）表示产出Y；时期t和时期t+1的距离函数分别用Dti（xti,yti）和Dti（xt+1i,yt+1i）表示。从t时期到t+1时期的Malmquist数量指数定义为（以技术Tt为参照）：

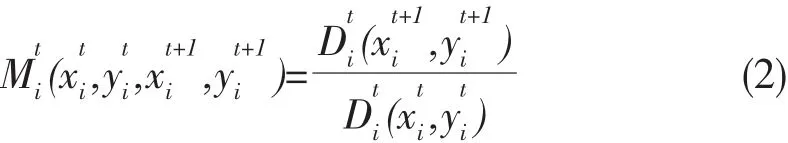
同理，以技术Tt+1为参照的Malmquist数量指数为：

以上得到的 Malmquist TFP指数具有良好的性质，可以分解为不变规模报酬假定下技术进步指数（TCP）和技术效率变化指数 （TEC），分解过程如下：

其中技术效率变化指数（TEC）还可进一步分解为规模效率指数（SEC）和纯技术效率指数（PTEC），即：

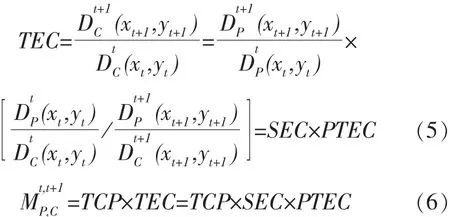
（三）投入产出设计

本研究选择劳动力（L）和资本存量（K）作为生产投入要素，以地区生产总值（GDP）作为产出要素计算出海西20个城市1995-2012年的全要素生产率（TFP）。根据海西经济区各个地区的统计年鉴公布的GDP数据、从业人数，作为产出Y、劳动力（L）的面板数据。

由于无法获取现成的海西经济区各个地区的资本存量数据，本文选取戈德·史密斯（Gold Smith）的基本公式：

式（7）中，Kit表示第i个城市第t年的资本存量，Iit表示第i个城市第t年的投资额，Pit为各城市固定资产投资价格指数，δt指的是第t年的资本折旧率.在资本折旧率的选取方面，假设每年资本折旧率是不变的，即δt取常用值9.6%，固定资产投资价格指数Pit可从各地区统计年鉴得到。据此，可计算出海西经济区各地区1995-2012年的资本存量值[12]。

三、实证结果及分析

（一）海西经济区Malmquist TFP指数综述

1.1995-2012年海西经济区Malmquist TFP指数分析

表1 海西经济区1995-2012年TFP指数及分解

1995-2012年海西经济区18年的平均TFP为1.027（表1），其增长的平均率为2.7%，达到了全要素生产率（TFP）的效率前沿。其中技术效率增长率为1.3%，技术进步平均增长率为9.3%，技术进步一直发挥正面效应，但是纯技术效率在1995-2012年平均增长率为负，即平均增长率为负1.4%。然而经济规模效率所带来的TFP的平均增长率也为负0.5%。1995-2002年全要素生产率指数出现正增长，其中2002年的增幅最大，达到了10.6%，而2003-2007年及2010-2012年全要素生产率指数呈负增长。

2.1995-2012年海西经济区各地区的Malmquist TFP指数分析

海西经济区16个城市1995-2012年TFP变化平均值为1.024（表2），平均增长率为2.4%，主要原因是技术的进步，其增长率为4.4%，但技术效率一直呈现下降的趋势。从表2的分析可知，纯技术效率和规模效率不能达到效率前沿。比较各个城市全要素生产率， 除了抚州 （0.935），南平 （0.892），漳州（0.946），梅州（0.897）的四个城市出现负增长，其他城市都出现了正增长。技术效率下降比纯技术效率、规模效率下降多，技术效率的大幅度下降是引起各城市全要素下降的主要因素之一。同时，虽然技术进步在此期间是呈现上升趋势，然而技术进步无法弥补技术效率下降所引起的全要素生产率的下降，因此海西经济区各个城市全要素生产率呈现下降趋势。

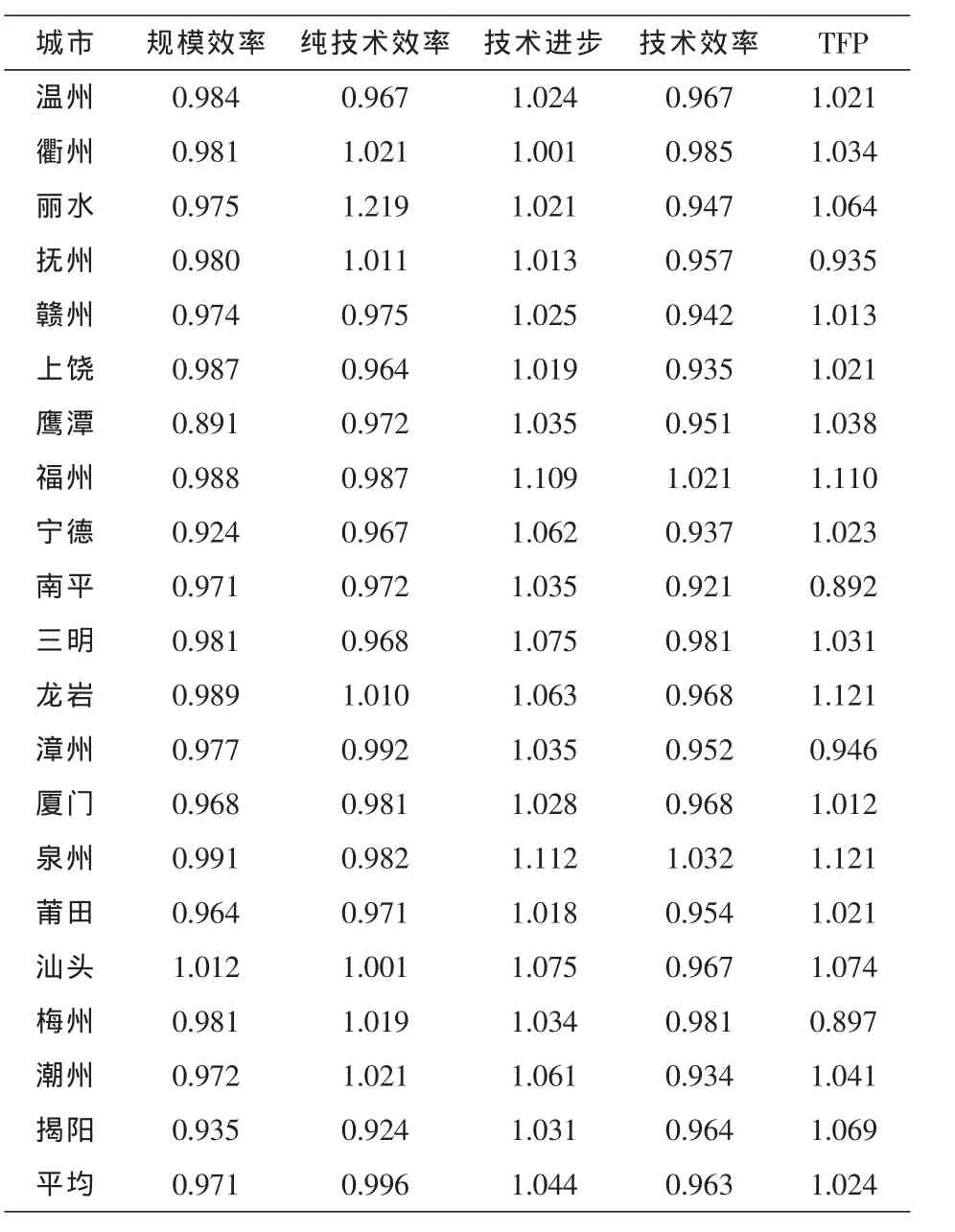
表2 1995-2012年海西经济区各地区的TFP指数及分解

（二）1995-2012年海西经济区各个城市全要素生产率指数分析

由表1可知，1995-2002年全要素生产率指数出现正增长，其中2002年的增幅最大，而2003-2007年及2010-2012年全要素生产率指数呈负增长。可见2002年是一个分界线，因此，在研究海西经济区各个城市的TFP的变化情况时，分1995-2002年和2003-2012年两个阶段分析海西经济区各个城市的TFP的变化情况。

1.1995-2002年海西经济区各个城市全要素生产率指数分析

1995-2002年期间，海西经济区TFP变化平均值为1.143（图1），即海西经济区在此期间的平均增长14.3%，呈现出较高增长率的趋势。引起这一时期TFP平均值较高的是技术效率在此时期提高较大，平均增长达到20%，规模效率及纯技术效率分别提高12.5%、4.7%，但技术进步出现了负增长，增长率为-5.1%。在此时期海西经济区处于经济快速增长的初始阶段，经济发展规模较小，全要素生产率的贡献较为明显。除了南平（0.878）和梅州（0.915）全要素生产率出现了负增长，其他城市全要素生产率增长趋势均为正，但大部分城市的技术进步都呈下降趋势。

图1 1995-2000年海西经济区各个城市TFP变动及分解

2.2003-2012年海西经济区各个城市全要素生产率指数分析

2003-2012年期间，海西经济区TFP变化的平均值为0.971（图2），低于效率的临界值，即表明海西经济区TFP平均增长率为-2.9%。结果与1995-2002年TFP指数的平均值14.3%相比，情况恰好相反，分析其主要原因是由于在此期间技术效率、纯技术效率和规模效率的下降，下降率幅度分别达到了9.2%，4.2%和5.2%.实证分析表明，在此期间技术进步是增加，增幅达到5.7%，由于其增长率低于技术效率下降的速度，因此其使该阶段的全要素生产率下降.从图2看，全要素生产率增长最高的是汕头和潮州，分别为14.5%、9.6%。技术进步和技术效率增长率的提高是引起这两个地区全要素增长的主要因素，对比发现其他城市在此期间却出现了技术效率下降的情况。与全要素生产率的实现效率前沿城市比较，只是这些城市的技术进步的增长比技术效率下降速度更快，确保全要素生产率的增长是正向的。因此，在资源配置效率方面，海西经济区大部分城市仍有很大的潜力。

图2 1995-2000年海西经济区各个城市TFP变动及分解

四、TFP的影响因素分析

（一）Tobit回归模型

由于全要素生产率不可能为负值，因此存在数据被截断.如果采用最小二乘法来估计该模型，得到的估计是有偏和不一致的，因此，为了回避该问题，本文选取Tobit回归模型（也称截取回归模型），该模型属于因变量受到限制的一种回归分析法。采用该模型有效的回避了因变量值受限制或数据被截的问题，最后采用极大似然法估计模型参数。选择的被解释变量为海西经济区的20个城市的TFP值，影响TFP因素包括人力资本（LAB）、技术进步（H）和劳动力增长率（IND）等变量.回归模型如下：

其中，μt~N（0,σ2）。用 f（z）表示标准正态分布概率密度，F（z）表示它的累积密度.则TFPt为正的观察值的联合概率密度为：

（二）影响因素选择

一是产业结构：产业结构就是指第一产业、第二产业、第三产业这三层产业在该区域生产总值占的比重，本文选取的产业结构指标是海西经济区各个城市中第二产业（IND2）、第三产业（IND3）占不同城市生产总值（GDP）的比重，所占比例不同表示其产业结构不同，产业结构是反映一个区域的资源配置、经济调整情况，是影响经济发展的重要因素。二是技术进步：技术进步程度不同表示各区域之间自主研发能力、学习模仿能力的大小不同，是影响技术进步的主要因数。因此，考虑这些因数，选取该些区域的出口总额（IMP）和实际利用外资额（FDI）占该区域GDP的比重和该些区域在科技上的投入 （KX）占该区域财政支出的比重等表示技术进步。三是人力资本（LAB）：为了便于数据的取得，本文采用该地区60岁以下的大学毕业人数占所有就业人数的比重来表示。

（三）回归结果及分析

选取海西经济区20个城市经济数据，得到下面方程：

方程下面括号内数字为每个系数t统计量值。

1.产业结构

从（6）式看出，IND3、IND2两变量系数检验是不显著的，即产业结构调整系数检验不显著，这就说明1995-2012年产业结构调整对海西经济全要素生产率的提高作用不明显。其根源是虽然国家提出加速海西经济区的发展，并给予一定的政策支持，但海西经济区的经济方式未得到根本性的改变，还是属于粗放型的增长方式。从海西区域经济结构来看，劳动密集型、传统产业为主，高科技含量、高技术产业、高附值等高新型产业还是比较少。

同时由于产业结构的调整会引起资源的不合理的配置，例如从原本资源利用率较高的部门流动到利用率较低的部门，这样产业结构的调整反而会影响该区域的TFP提高，因此影响整体经济增长的质量和效益。

2.技术进步

回归方程中的FDI系数是不显著的，表明外商直接投资对于TFP的影响也是作用不显著。从外商在海西经济区投资结构来看，外商在海西经济区的投资主要是利用这些区域廉价的劳动力、土地环境资源及当地政府给予外资企业一些优惠的政策。因此，出于这些投资条件的考虑，外资企业主要投资在一些劳动密集型和资源高耗型的加工业。而在一些高技术性、资金密集型的机电、器材制造、电子科技及通信设备制造行业投入的较少。因此外商投资对于推动海西经济的发展贡献是有限的。

科技上的投入KX系数检验显著，当地政府每增加科技投入占地方财政支出的比重如果提高1%，TFP将提高4.0231%。科技的投入促进了当地技术进步，从而有利于TFP的提高。进出口IMP系数检验也是显著，表明如果当地进出口占该区域GDP的比重每增加1%，该区域TFP会因此而提高0.113%。相对科技投入对当地TFP的影响相比，进出口对当地TFP的影响的微弱的。海西经济区贸易方式主要以加工型贸易为主，由于加工贸易主要集中在劳动密集型的简单加工装配为主，深层次的加工较少，高附值少，技术含量较低，从而对一区域技术进步和TFP的作用不明显。

3.人力资本

人力资本LAB的回归系数检验不显著，而且其对区域的TFP影响是反方向的。根据人力资本阀值理论，一个地区的人力资本投入如果未达到促使该区域R&D活动活跃的临界值，那么就不利于该区域的技术进步和全要素增长率的提高。因此，从回归结果看，海西经济区的人力资本投入还不够，未达到促进技术进步的临界值。建议海西经济区各地方政府要加大人力资本的投入，例如加大人才的引荐，创造有利的条件去吸引高素质人才来海西工作等等，有利于海西各城市TFP的提高。

五、结论及政策建议

（一）结论

实证研究表明，在研究的样本范围内，海西经济区的平均全要素生产率达到有效值。1995-2002年主要是技术效率的提升促进了全要素生产率的增长；2003-2012年主要是技术进步的提高促进全要素生产率的增长。Tobit模型回归结果表明，人力资本对这些区域的全要素生产率的增长作用是不显著的，甚至是反向的。科技投入对全要素生产率的增长影响比较显著，即当地政府科技投入占地方财政支出的比重如果提高1%，全要素生产率的增长将提高4.02%。但由于海西经济区整体经济还未从粗放型的发展模式向集约型发展模式转变，即主要还是集中在那些劳动密集型、科技附加值较低的行业。与一些经济发达地区相比，在科技研发、教育培训等方面的财政投入较少，使得海西经济区产业科技水平较低。

（二）政策建议

海西经济区各地方政府应该增加教育、科研的投入，加大人才引进力度，以此促进本地区的技术进步、全要素生产率增长，从而使海西经济真正走上集约型的发展道路。对此，提出以下几点建议：首先，海西经济区仍需进一步提高产业结构高度化、加大产业结构中的科技含量。除了通过进口高技术的机器设备外，更重要的是要提高自身的创新能力，提高技术效率，并且在政策方面给予高新技术产业和第三产业提供更大的优惠。其次，要提高引进外资的质量。技术溢出是外商直接投资的一种内在功能，其溢出效应的强弱不仅受外资企业技术先进程度的制约，还与东道国自身技术吸收能力有很强的关联。因此，要特别支持那些有可能同时带来后向关联和前向关联的、涉及中间产品生产行业的发展，充分发挥外资企业的产业带动效果，实现产业结构升级。最后，要重视人力资本的投资。加大文化教育费用和科学研究费用的投入，在财政方面给予更大地支持，提高对外资技术溢出的吸收能力和自主创新能力，促进技术进步、全要素生产率增长，从而使海西经济真正走上集约型的发展道路。

：

[1]易纲，樊纲，李岩.关于中国经济增长与TFP的理论思考[J].经济研究,2003（8）：62-68.

[2]张军，施少华.中国经济TFP变动1952-1998[J].世界经济文汇,2003（2）：104-112.

[3]颜鹏飞，王兵.技术效率、技术进步与生产率增长:基于DEA的实证分析[J].经济研究,2004（12）：165-175.

[4]郭庆旺，贾俊雪.中国TFP的估算——1979-2004[J].经济研究,2005（5）：125-133.

[5]郭庆旺，赵志耘，贾俊雪.中国省份经济的TFP分析[J].世界经济,2005（5）：204-213.

[6]章祥荪，贵斌威.中国TFP分析——Malmquist指数法评述与应用[J].数量经济技术经济研究,2008（6）：25-33.

[7]叶德磊，邓金鹏.中国三大地区全要素生产率的比较分析[J].华东师范大学学报（哲学社会科学版），2010（1）：102-107.

[8]邓利方，余甫功.广东TFP的测算与分析——基于面板数据的Malmquist DEA[J].广东社会科学,2006（5）：120-129.

[9]Jeffrey Wooldridge.面板数据的计量经济分析[M].北京：机械工业出版社，2008.

[10]Malmquist，S..Index Numbers and Indifference Surfaces[J].Trabajos de Estadistica，1982（50）:209-242.

[11]Caves，D.W.，Christensen，L.R.，and W.E.Diewert，The Economic Theory of Index Numbers and the Measurement of Input，Output，and Productivity[J].Econometrica 50（1982）:1393-1414.

[12]张军，吴桂英，张吉鹏.中国省级物质资本存量估算:1952-2000[J].经济研究,2004（10）:105-132.