基于负熵的随机双梯度算法
2014-09-01卢中宁初元红
卢中宁,初元红
(1.郑州轻工业学院计算机与通信工程学院, 中国 郑州 450002; 2.黄河科技学院,中国 郑州 450063)
基于负熵的随机双梯度算法
卢中宁1,初元红2*
(1.郑州轻工业学院计算机与通信工程学院, 中国 郑州 450002; 2.黄河科技学院,中国 郑州 450063)
随机双梯度算法是独立分量分析中一个重要的学习算法,但该算法收敛速度慢,稳态误差大,不利于信号的准确适时性处理.论文重点对随机双梯度算法进行了改进,提出一种基于负熵的随机双梯度算法.在改进的算法中,用负熵来度量其中的随机变量非高斯性,从而来克服峭度的不稳健性.论文最后通过理论分析和仿真实验证明这种改进的随机双梯度算法具有较好的分离效果且稳定性高.
随机双梯度算法;独立分量分析;负熵;峭度
独立分量分析(ICA)依据独立原则为多维观察信号建立目标函数,利用某种学习算法把这些信号分解成若干独立成分以实现增强和恢复信号的目的,目前已成为一种十分有效的盲信号分离技术[1-2].从这个定义可以看出,独立分量分析算法由目标函数和学习算法组成.不同的目标函数、学习算法构成的独立分量分析算法不同[3-4].一般来说,处理对象确立了,目标函数也就很容易确定了[5-6].独立分量分析算法的收敛速度、稳定性也取决于所选择的学习算法[7-8].这使得学习算法的研究成为独立分量分析中的一个中心任务.
目前在独立分量分析中也出现了一些较优秀的学习算法[9-12].然而,在独立分量分析中,不管最终选择哪种学习算法,都要在最终的信号分析时具有较快的收敛速度和较小的稳态误差[13].在众多独立分量分析的学习算法中,随机双梯度算法是在随机梯度法、自然梯度法、相对梯度法基础上进行的一种改进算法[14],虽然性能较原始算法有很大程度上,但是它因采用峭度为目标函数而易受大幅随机脉冲干扰的影响.为此,论文重点对随机双梯度算法进行改进并进行仿真对比实验.
1 随机梯度算法
随机梯度算法是独立分量分析中一类较简单学习算法.例如独立分量分析以公式(1)为目标函数:
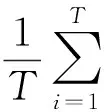
(1)
对式(1)进行求导可得:
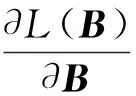
(2)
采用随机梯度和随机逼近,即可获得随机梯度ICA算法:
B(n+1)=B(n)+μ[B-T-Φ(y)xT].
(3)
该算法优点在于:在波动性较大的情况下,该算法能够快速调整学习方向,使算法向正确方向行进.然而,由于涉及到了矩阵优化,且该矩阵一般是高阶矩阵,这无疑大大增加了求解式(3)的计算量.而且,该算法收敛速度慢,同时还需要对迭代步长的设置有较高的要求.如果迭代步长设置不恰当,那么该算法就很可能失去收敛性.
后来出现的自然梯度算法和相对梯度算法,都是对随机梯度算法的改进,这两个算法本质上基本一致.例如,以公式(1)为例,对其使用自然的梯度,即可获得如下的自然梯度ICA算法:
B(n+1)=B(n)+μ[B(n)-T-Φ(y)xT]BT(n)B(n) =B(n)+μ[I-Φ(y)yT]B(n).
(4)
它们同随机梯度算法缺点一样,那就是矩阵逆的存在大大增加了求解的计算量.
2 随机双梯度算法
随机双梯度算法是在随机梯度算法、自然梯度算法的基础上进行的改进.
假设白化后的数据z(t)=[z1(t),…,zm(t)]中各分量相互独立,也即E[z(t)z(t)T]=I,此时衡量测量信号输出分量独立性的准则函数定义为
J(B)=J1(B)+σJ2(B).
(5)
随机双梯度算法一般使用输出信号的高阶累积量作为衡量测量信号输出分量统计独立性的准则函数,也即采用峭度的平方作为衡量测量信号输出分量统计独立性的准则函数.同四阶矩阵相比,输出信号的四阶累积量更能完整地描述输出信号的特征,因此一般就把输出信号的四阶累积量引入到准则函数之中:
(6)
式(6)中J1(B)使用输出信号的峭度作为分离准则.
J2(B)=‖BBT-I‖.
(7)
式(7)中J2(B)表示分离矩阵要满足正交性.
采用随机梯度对J1(B)和J2(B)进行如下优化
▽J1(B)=-E[y4]E[y3]+3E[y3],
(8)
▽J2(B)=(BBT-I)B.
(9)
把式(8)和式(9)代入公式(5)即得
▽J(B)=-{E[y4]E[y3]+3E[y3]}z(t)-σ(BBT-I)B.
(10)
然后采用瞬时值来替代期望均值即可获得分离矩阵B的更新公式:
B(t+1)=B(t)-α(y(t)7-3y(t)3)zT(t)-β(B(t)B(t)T-I)B(t).
(11)
因为该算法包含了2个随机学习步长α和β,因此其称为随机双梯度算法.
3 随机双梯度算法的改进
在随机双梯度算法中采用了峭度作为目标函数,而由于峭度是不稳定的,这就导致利用峭度寻找独立分量时易受大幅度随机脉冲干扰的影响.由于负熵不受大幅度随机脉冲的影响,因此,论文将采用负熵来度量随机变量的非高斯性以克服峭度的不稳健性.
这里还用公式(5)作为衡量测量信号输出分量独立性的准则函数,则用高阶积累来近似表达负熵如下:
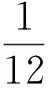
(12)
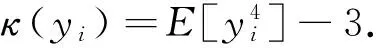

(13)
则可得分离矩阵的更新公式为
B(t+1)=B(t)+α(y(t)5-y(t)7+3y(t)3)zT(t)-β(B(t)B(t)T-I)B(t).
(14)
利用公式(14)进行随机变量的独立性寻找时,该算法即为基于负熵的随机双梯度算法,也即本文提出的改进算法.
下面为改进算法的简单过程描述.
Step 1:初始化算法所需变量;
Step 2:利用u(t+1)=u(t)+η(t)[I-z(t)z(t)T]u(t)对观测数据进行白化处理;
Step 3:依据公式(15)求B(t+1)分离矩阵;
Step 4:令t=t+1,转到Step 3,直到满足设定的终止条件,算法结束.
4 仿真实验
在该仿真实验中,图1和图2为两个独立的语音信号s1和s2,对它们采用Matlab数学工具进行混合以生成一个混合矩阵,从而获得如图3和图4的两个混合语音信号.利用本文所提的基于负熵的随机双梯度算法对图3和图4进行分离结果如图5和图6所示,传统随机双梯度算法对图3和图4进行分离,结果如图7和图8所示.

图1 原语音信号s1 图2 原语音信号s2Fig.1 Original speech signal s1 Fig.2 Original speech signal s2

图3 混合语音信号x1 图4 混合语音信号x2Fig.3 Mixed speech signal x1 Fig.4 Mixed speech signal x2
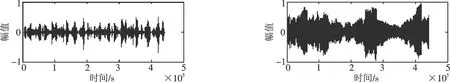
图5 本文算法分离后的语音信号 图6 本文算法分离后的语音信号Fig.5 Separated speech signal by proposed algorithm Fig.6 Separated speech signal by proposed algorithm

图7 传统算法分离后的语音信号 图8 传统算法分离后的语音信号Fig.7 Separated speech signal by traditional algorithm Fig.8 Separated speech signal by traditional algorithm
为了进一步证明本文算法性能的优越性,下面给出这两种算法下原语音信号与对应分离信号之间的相关系数.其结果如表1所示.

表1 两种算法下原语音信号与分离信号的相关系数
从上述仿真实验结果来看,同传统算法相比,论文所提的基于负熵的随机双梯度算法能够分离出与原信号较为接近的信号,据此可知,本文改进算法是可行的.
5 结束语
研究了传统随机双梯度算法,指出其因采用峭度作为目标函数而导致寻找独立分量时易受大幅度随机脉冲干扰影响方面的不足,提出利用负熵作为衡量信号量独立性的构想并给出一个改进的随机双梯度算法,并通过仿真实验证明了该算法的有效性.
[1] 吴宏天,刘 辉.基于方差和峭度的模拟电路故障诊断[J].湖南师范大学自然科学学报, 2011,34(5):32-36.
[2] 傅丽华,何燕子,朱 云.长株潭核心区土地利用生态风险驱动因子分析[J]. 湖南师范大学自然科学学报, 2012,35(5):85-89.
[3] 易灵芝,龚会茹,沈建飞.基于相关因子的太阳能光伏发电系统互补复合孤岛检测研究[J].湘潭大学学报:自然科学版, 2011,33(4):100-104.
[4] 赵知劲, 陈 林, 王海泉. 基于独立分量分析的实正交空时分组码盲识别[J].通信学报, 2012,33(11):1-7.
[5] 王冬冬.基于独立分量分析的热波检测图像增强[J].科学技术与工程, 2013,13(2):512-515.
[6] 杨俊美,余 华,韦 岗. 独立分量分析及其在信号处理中的应用[J].华南理工大学学报:自然科学版, 2012,40(11):1-12.
[7] 吕淑平,方兴杰. 基于独立分量分析的自适应在线算法[J].计算机应用研究, 2010,27(11):4140-4143.
[8] 于 淼,王曰海,汪国富.基于独立分量分析的跳频通信抗梳状阻塞干扰方法[J]. 解放军理工大学学报:自然科学版, 2012,13(6):593-598.
[9] 欧世峰,高 颖,赵晓晖.基于随机梯度的变动量因子自适应白化算法[J].自动化学报, 2012,38(8):1370-1374.
[10] 王法松,张林让.基于自然梯度的独立子空间盲信号处理方法[J]. 南京大学学报:自然科学版, 2011,47(4):420-425.
[11] 程 娇,王晓凯,李 锋.独立分量分析可调速率相对梯度算法[J]. 信息与电子工程, 2010,8(2):207-211.
[12] 初铭畅,熊晓路,于 洋.因子分析在创新型科技人才竞争力评价中的应用[J]. 辽宁工业大学学报:自然科学版, 2012,32(5):343-346.
[13] 张和发,李立萍. 含噪独立分量分析的期望最大化算法[J].电子科技大学学报, 2012,41(4):527-531.
[14] 高 涛.组合2DFLDA监督的非负矩阵分解和独立分量分析的特征提取方法[J]. 计算机应用研究, 2012,29(4):1588-1590.
(编辑 胡文杰)
Stochastic Dual-Gradient Algorithm Based on Negative Entropy
LUZhong-ning1,CHUYuan-hong2*
(1.School of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China;2.Huanghe Science and Technology College, Zhengzhou 450063, China)
Stochastic dual-gradient algorithm is an important learning algorithm of independent component analysis, whose convergence speed is slow and steady-state error is large, which leads to inaccuracy in timely signal processing. Focusing on the improvement of stochastic dual-gradient algorithm, a stochastic dual-gradient algorithm based on negative entropy is proposed, in which negative entropy is used to measure the non-Gaussian of random variables and thus to overcome the kurtosis of robustness in the improved algorithm. By theoretical analysis and simulation experiments the paper finally proves that the improved Stochastic Dual-Gradient Algorithm has better separation effect and higher stability.
stochastic dual-gradient algorithm; independent component analysis; negative entropy; kurtosis
2013-04-23
国家自然科学基金资助项目(60970084)
*
,E-mail:chuyuanh@163.com
TP301.6
A
1000-2537(2014)04-0084-04
