用改进的Newton法求解非线性奇异问题

初元红,孙贵玲

(黄河科技学院，中国 郑州 450063)

用改进的Newton法求解非线性奇异问题

初元红*,孙贵玲

(黄河科技学院，中国 郑州 450063)

在Hilbert空间，将外推技巧和Newton法相结合，得到新的迭代格式.用其求解奇异问题，使改进的Newton法收敛速率由0.5提高到0.333 3．此结论对一般的Banach空间同样适用.

Hilbert空间；改进的Newton法；奇异问题

设F是Hilbert空间E上的C3非线性算子，x*是非线性方程

F(x)=0

(1)

的解(即F(x*)=0)．解非线性方程最重要的方法之一是Newton法，它的迭代程序如下：

xn+1=xn-F′(xn)-1F(xn).

(2)

当F′(x*)是奇异的(即F′(x*)-1不存在)，Newton法在一个星形区域内仍然收敛，且在x*处的收敛率为0.5[1]．本文利用Hilbert空间的几何特征，将外推技巧和Newton法相结合，用来求解非线性奇异问题，得到新的迭代格式，使Newton法的收敛率由0.5提高到0.333 3，提高了算法的效用．

1 主要引理

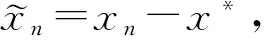
引理1[1-4]设(1)dim(N)=1，(2)F″(x*)(N,N)∩X={0}，(3) ‖F″(x*)nx‖≥c1·‖n‖·‖x‖ 其中n∈N,x∈X,c1>0，则存在ρ>0,θ>0，使得当x∈w(ρ,θ)，F′(x)-1存在，映射Gx=x-F′(x)-1F(x)为w(ρ,θ)到自身的映射，且存在C1>0,对于任意x∈w(ρ,θ)，有‖F′(x)-1‖≤C1‖x-x*‖-1．此外，若x0∈w(ρ,θ)，xn+1=G(xn)，则序列{xn}收敛于x*，且有下列估计：

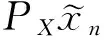
(3)

(4)

引理2[5]设E是Hilbert空间，∀x,y∈E，t为参数，则有

‖tx+(1-t)y‖2=t‖x‖2+(1-t)‖y‖2-t(1-t)‖x-y‖2.

(5)

引理3[6]存在C3>0，对任意的y∈X，x∈w(ρ,θ)，有‖F′(x)y‖≥C3‖y‖.

2 主要定理

根据[7-10]作者提出如下改进迭代格式：

(6)

这里tn是依赖于n的待定常数．在奇异点附近，Newton在F′(x*)的零空间N方向收敛速度特别慢，作者主要想法是选择适当tn，从而加速迭代格式(6) 的收敛速度．

(7)

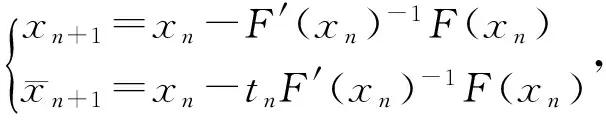
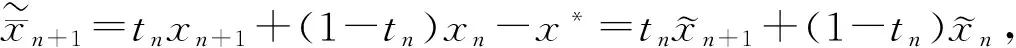
利用Hilbert空间的特征等式(5)得：

(8)

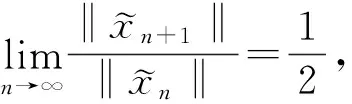
(9)

(10)

下面估计‖xn+1-xn‖.由Newton法xn+1=xn-F′(xn)-1F(xn)可知：

xn+1-xn=-F′(xn)-1F(xn).

利用泰勒展开式有：

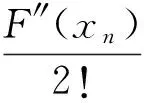
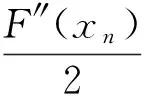
两边同乘F′(xn)-1得：

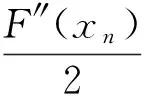
(11)

再由泰勒展开式：

F′(x*)=F′(xn)+F″(xn)(x*-xn)+β2(xn),

F″(xn)(x*-xn)=F′(x*)-F′(xn)+β2(xn).

(12)

将(12)代入(11)得：

由(10)得：

两边同时除以‖xn-x*‖得：

(13)

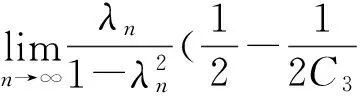
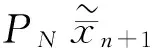
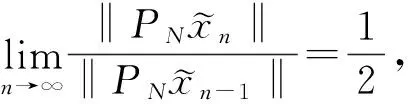
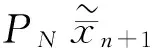
这说明对于一般的Banach空间，改进的Newton法在零空间收敛的速度为0.333 3，提高了算法的收敛速度．

3 计算实例

取初始点x0=0.5、y0=1，部分计算结果见表1．

表1 部分计算结果

[1] RALL L B. Convergence of the Newton process to multiple solution[J]. Numer Math, 1966,9(1):23-37.

[2] REDDIEN G W. On Newton’s method for singular problems[J]. SIAM J Numer Anal, 1978,15(5):993-996.

[3] DECKER D W, KELLER H B, KELLEY C T. Convergence rates for Newton’s method at singular points[J]. SIAM J Numer Anal, 1983,20(2):296-314.

[4] DECKER D W, KELLEY C T. Convergence acceleration for Newton’s method at singular point[J]. SIAM J Numer Anal, 1982,19(1):219-229.

[5] 徐宗本.Lp空间特征不等式及应用[J]. 数学学报, 1989,12(2):209-218.

[6] 刘炳初. 泛函分析[M]. 北京：科学出版社, 2004.

[7] 杨忠华.弦法在奇异点处一个改进格式[J].高等计算数学学报, 1990(2):151-157.

[8] 潘状元. 求解奇异问题加速迭代格式的构造[J].工程数学学报, 1997,14(2):59-64.

[9] 初元红,潘状元，刘晓敏.用修正的Broyden方法求解奇异问题[J].哈尔滨理工大学学报, 2006,11(1):39-42.

[10] 王 颖,潘状元.用行列修正拟Newton法求解奇异问题[J]. 哈尔滨理工大学学报, 2010,15(4):64-67.

(编辑 胡文杰)

The Modified Newton Method for Solving Nonlinear Singular Problems

CHUYuan-hong*,SUNGui-ling

(Huanghe Science and Technology College, Zhengzhou 450063, China)

In Hilbert space, the singular problems are solved by using the combination of modified Newton method and the extrapolation technique. The modified Newton method is shown to yield a new sequence that improves the convergence rate from 0.5 to 0.333 3. The conclusion is also applied to a Banach space.

Hilbert space; modified Newton method; singular problems

2013-01-08

郑州市科技局资助项目(20141374，20141375);黄河科技学院教改资助项目(MJ2012014)

*

,E-mail：chuyuanh@163.com

O241

A

1000-2537(2014)05-0081-04