自捻纱线强力的Weibull分布预测
2014-08-31肖志永姚兴川
肖志永,崔 红,姚兴川
(1.天津宏大纺织机械有限公司,天津 300384; 2.盐城工学院 纺织服装学院,江苏 盐城 224000;3.江苏南纬悦达纺织研究院,江苏 盐城 224000)
自捻纱线强力的Weibull分布预测
肖志永1,崔 红2,姚兴川3
(1.天津宏大纺织机械有限公司,天津 300384; 2.盐城工学院 纺织服装学院,江苏 盐城 224000;3.江苏南纬悦达纺织研究院,江苏 盐城 224000)
通过实验对自捻纱线不同夹持长度下的断裂强度进行Weibull分布分析,纯腈纶自捻纱断裂强度的线性拟合相关系数的平方R2达到0.92~0.98,说明纯腈纶自捻纱的断裂强度符合Weibull分布,可以用Weibull分布来预测自捻纱线的断裂强度.同一种纯腈自捻纱线在不同夹持隔距下的Weibull模量是不同的,120 mm夹持隔距测试有捻区时Weibull模量β最大,表明腈纶自捻纱线的拉伸断裂强度值的离散性最小,其拉伸断裂强度的均匀性和可靠性最高.夹持隔距110 mm时,有捻区拉伸时η值最大,表明此时腈纶自捻纱的平均断裂强度最大.
自捻纱线;断裂强度;Weibull分布;夹持隔距;预测
纺纱方法决定成纱结构,而成纱结构又主要影响纱线的断裂强力和断裂伸长率.纱线的强力不仅影响到最终成品的质量水平,而且影响到整个纺织生产过程包括纺纱、织造、印染以及后整理过程的生产效率,所以纱线强力研究一直是纺织界的热点,也是纺织科学中的经典问题,自捻纱线的强力特别是腈纶自捻纱的强力值得研究.
文献对于纱线强力的研究体现了多样化的特点.如Hearle[1]的短纤维纱线近似力学理论,由纤维性能结合成纱结构推导出环锭纱线强力.Zurek等[2]根据单纤维的应力-应变曲线的分析和纤维性能如直径、长度、单纤维强度以及纱线线密度、捻度与CV值建立数学模型,预测棉纱的强力和断裂伸长率.文献[3-4]利用神经网络对纱线强力进行了预测.严广松[5]用概率统计的方法分析了纤维长度、细度不匀并预测了棉纱线的强力性能.Bogdan[6]和Verbeck[7]用统计的方法进行研究,建立了非线性模型,预测不同结构(C—纱线支数,P—纤维本身强力,B—纱中纤维的倾斜角度)和工艺设计参数(F—牵伸倍数,M—捻系数,T—假捻)纱线的断裂强力
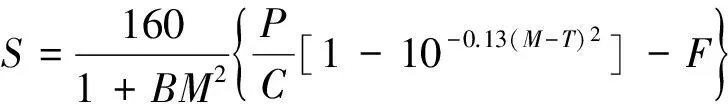
(1)
Pan[8-10]的短纤维纱线力学机理主要依据了Peirce的弱环理论和Phoenix的纤维结构强力的链束理论,在分析了断裂现象与临界纤维长度Lc的关系式后得到了Weibull分布的均值和方差,给出了纤维束强力和单纤维强力之间的关系,首次用数学方法在综合考虑纤维性能和成纱结构的基础上对纱线强力进行了预测,得到了人们肯定.近年来,人工神经网络技术的应用使预测手段得到了广泛应用,但是仅仅对输入输出的处理没有能够考虑很重要的纺纱工艺和纱线具体的成纱状况,纱线强力预测的准确度不高.综上所述,基于结构的方法更加具有揭示内在原理的意义.
Weibull分布[11]是以脆性材料的最弱连接为基础的,也就是以弱环定理为基础.Weibull分布在纺织上首先应用于纺织纤维强力的研究.最早利用Weibull分布模型对纤维强度分布进行研究的是Coleman[12],他证实了脆性单纤维的强度分布函数符合以弱环理论为基础的二参数Weibull分布.后来的很多研究都证实了芳纶、碳纤维等高性能纤维的强力都符合Weibull分布[13-16].很多研究集中于纱线的强力性能如环锭纱线、气流纱线、摩擦纺纱线以及喷气纺纱线的分布,对于纱线的强度分布进行了拟合,并认为纱线强度符合Weibull分布,但是将其运用到自捻纺纱线还少有人研究.自捻纱线的特点是存在明显的弱捻区域,根据弱环定理,纱线断裂肯定都发生在弱捻区域.可以通过Weibull分布的预测模型来预测自捻纱线的强力,研究自捻纱线的断裂特征,有助于找到影响纱线断裂的特征因素,提高自捻纱线的性能.
1 二参数的Weibull 分布
三参数Weibull分布的分布函数形式为
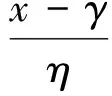
(2)
其中,η为尺度参数,β为形状参数,γ为位置参数.
当γ=0时,上式蜕变为二参数Weibull分布:
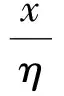
(3)
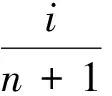
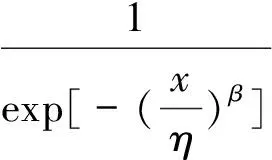
取对数后得到
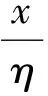
故
Yi=βXi+D.
(4)
式(4)为一直线,若用实验值估计式(4)的参数,即为Weibull概率图.对于二参数Weibull分布,如果在概率图上,X和Y的关系可回归为一直线且相关系数R接近1,则表明符合二参数Weibull分布.反之,则认为不符合二参数Weibull分布.根据Weibull分布的性质可知,F(x)为材料的断裂概率,x为纱线的断裂强度,η为特征寿命或尺度参数,代表纱线的特征断裂强度.η值越大,表示要分析的纱线的拉伸断裂强度值越大,β值越大说明纱线的平均强力较大.η叫做Weibull模量或形状参数,其值代表拉伸断裂强度概率分布累积函数的形状;β值越大表示纱线的拉伸断裂强度值的离散性越小,其拉伸断裂强度的均匀性和可靠性就越高.
2 自捻纱线强度的Weibull分布
在S300自捻纺纱系统上纺制纯腈纶(37.5×2)tex自捻纱线,并测试拉伸隔距为110 mm和120 mm时有捻段的断裂强度、无捻段的断裂强度和其在拉伸隔距为250 mm和500 mm时的断裂强度,分别得到(37.5×2)tex纯腈纶自捻纱不同夹持隔距下的断裂强度与伸长率(见表1)和断裂强度的Weibull线性拟合图(见图1).

表1 (37.5×2)tex纯腈纶自捻纱不同夹持隔距下的断裂强度与伸长率Tab.1 Breaking strength and elongation in different clamping length for (37.5×2)tex acrylic self-twisted yarns
由表1可以看出,在110 mm和120 mm夹持隔距时,有捻区的断裂强度和断裂伸长率明显高于无捻区的断裂强度和断裂伸长率,这是由于自捻纱线有捻区存在捻回,其结构与双股纱线相似,而无捻区仅在单根纱条上有部分捻回,所以该段断裂强度和断裂伸长率明显低于有捻段.除此之外,可以观察到有捻区拉伸的断裂强度CV值和断裂伸长率CV值明显低于无捻区段,这也和有捻区段具有捻回纱线结构较稳定而无捻纱段不存在股线捻回纱线结构较蓬松有关.从整体数据可以看出,随着夹持隔距的增加,纯腈自捻纱线的断裂强度逐渐变小,这是由于夹持隔距的增加导致了令纱线断裂的纱线弱节的概率随之增加的缘故.对于自捻纱线来讲,夹持隔距越大,无捻或弱捻区长度占夹持长度的比例就越大,会造成纱线断裂强度和断裂伸长率的降低.
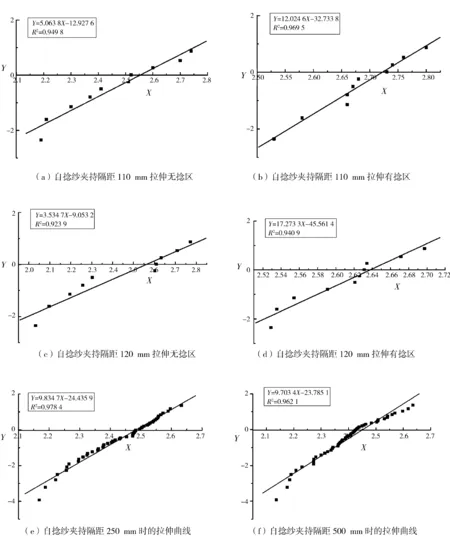
图1 自捻纱不同夹持隔距拉伸曲线Fig.1 Tensile curve of different clamping gauges for self-twisted yarns
由图1(a)至(f)可以看出,纯腈纶自捻纱的线性拟合相关系数R的平方(即R2)为0.92~0.98,表明-ln ln(1-F(x))和lnx之间有很好的线性关系.纯腈纶自捻纱的断裂强度符合Weibull分布,故可以用Weibull分布来预测自捻纱线的断裂强度.
不同夹持隔距下纯腈自捻纱的Weibull参数值见表2.Weibull模量β的大小是由纱线断裂强度的偏差所决定的,也就是测量的误差以及纱线断裂强度的离散造成了自捻纱模量值的差异.从表2中可以看出,同一种纯腈自捻纱线在不同夹持隔距下的Weibull模量是不同的.前面提到,其值越大,表示要分析的材料的拉伸断裂强度值的离散性越小,其拉伸断裂强力的均匀性和可靠性越高.120 mm夹持隔距测试有捻区时,Weibull模量β最大,这说明在120 mm夹持隔距拉伸有捻区时,自捻纱的拉伸断裂强度离散性最小,其拉伸断裂强力的均匀性和可靠性较高.
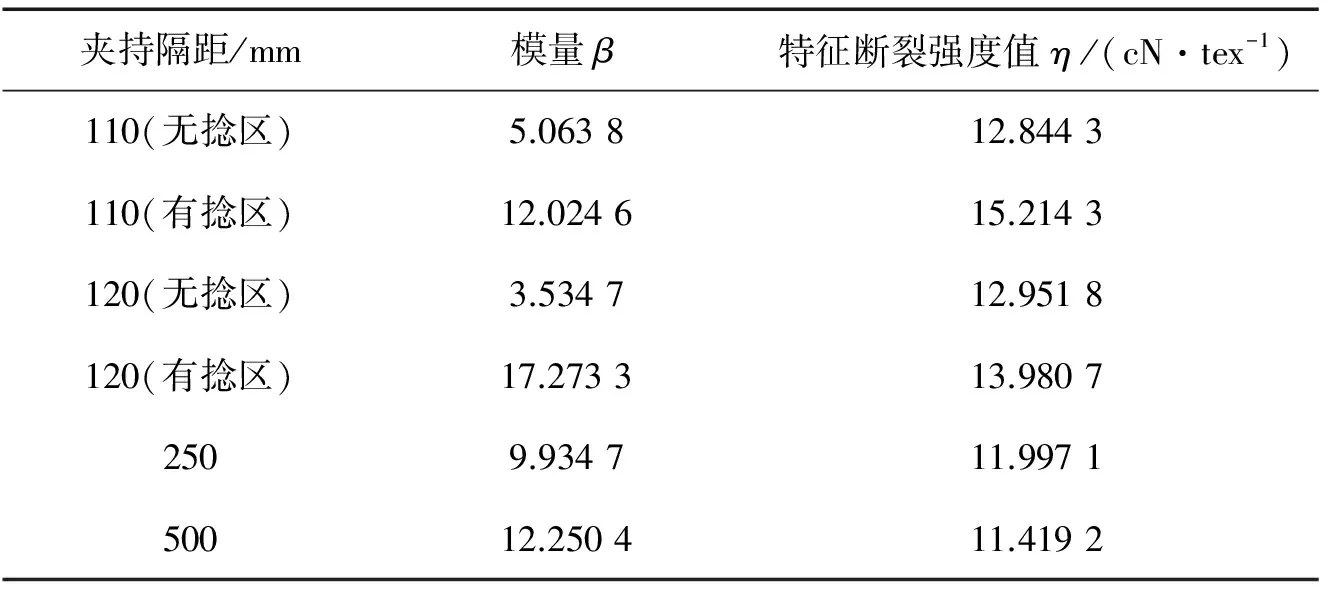
表2 (37.5×2)tex腈纶自捻纱的Weibull参数值Tab.2 Weibull parameters value for (37.5×2)tex acrylic self-twisted yarns
η值表示要分析的材料的特征拉伸断裂强度值,η值越大说明材料的平均强度较大.从表2中可以看出,当夹持隔距为110 mm时对有捻区进行拉伸,其η值最大,说明在这种情况下自捻纱的平均强度最大.
3 结论
通过实验对自捻纱线不同夹持长度下的断裂强度进行Weibull分布分析,纯腈纶自捻纱断裂强度的线性拟合相关系数的平方R2达到0.92~0.98,说明纯腈纶自捻纱的断裂强度符合Weibull分布,所以可以用Weibull分布来预测自捻纱线的断裂强度.同一种纯腈自捻纱线在不同夹持隔距下的Weibull模量是不同的,120 mm夹持隔距测试有捻区时,Weibull模量β最大,表明腈纶自捻纱线的拉伸断裂强度值的离散性最小,其拉伸断裂强度的均匀性和可靠性最高.夹持隔距为110 mm时,有捻区拉伸时η值最大,表明此时腈纶自捻纱的平均强度最大.
[1] Hearl J W,Bose O N.Migration of fibers in yarns,a geometrical explanation of migration[J].Textile Research Journal,1965(35):693.
[2] Zurek W,Frydrych I, Zakrzewski S. A method of predicting the strength and breaking strain of cotton yarn[J]. Textile Research Journal, 1987, 57(8): 439-444.
[3] Ramesh M C,Rajamaniekam R,Jayaraman S. The prediction of yarn tensile properties by using artificial neural networks[J].Textile Institute Journal,1995, 86(4): 459-469.
[4] 程文红,陆凯.利用人工神经网络进行纺纱技术预报[J].上海毛麻科技,2000(1):19-21.
[5] 严广松.基于密度函数方法的纤维长度分布影响分析[D].上海:东华大学,2009.
[6] Bogdan J F.The characterization of spinning quality[J].Textile Research Journal, 1956, 26(9): 720-730.
[7] Verbeck R. A statistical method of characterizing spinning quality[J].Textile Research Journal,1965, 35(l):1-14.
[8] Pan N. Development of a constitutive theory for short fiber yarns,mechanics of staple yarn without slippage effect[J].Textile Research Journal,1992(62):749-765.
[9] Pan N. Prediction of statistical strength of twisted fiber structures[J].Journal of Materials Science,1993(28):6107-6114.
[10]Pan N,Hua T.Relationship between fiber and yarn strength[J].Textile Research Journal,2001(71):960-964.
[11]Weibull W A.Statistical distribution function of wide applicability[J].Journal of Applied Mechanics,1951,7(3):293-297.
[12]Coleman B D.On the strength of classical fibers and fiber bundles[J].Journal of Mechanics and Physics on Solids,1958(7):60-72.
[13]吴琪琳,潘鼎.碳纤维的Weibull分析理论[J].高技术纤维与应用,1999,24(12): 41-44.
[14]吴琪琳.不同拉伸条件下基于Weibull模型的粘胶基碳纤维强度分布研究[J].合成纤维工业,2002,4(2):25-28.
[15]吴琪琳,潘鼎.国产粘胶基碳纤维强力的两种统计分布[J].材料导报,2000,14(1):55-56.
[16]唐维杰,顾明元.碳纤维强力的计算机研究[J].宇航学报,1996,17(3):40-45.
TheWeibullstrengthpredictionoftheself-twistyarn
XIAO Zhi-yong1,CUI Hong2,YAO Xing-chuan3
(1.TianjinHongdaTextileMachineryCompanyLimited,Tianjin300384,China;2.CollegeofTextilesandClothing,YanchengInstituteofTechnology,Yancheng224000,China;3.TRYDTextileResearchInstitute,Yancheng224000,China)
Through the experiment on the analysis of Weibull distribution of the breaking strength of self-twisted yarns in different clamping gauge, it is reached 0.92~0.98 for the square of correlation coefficient of linear fitting. It is proved that the breaking strength of the pure acrylic self-twisted yarns follows Weibull distribution, so Weibull distribution can be used to predict the breaking strength of pure acrylic self-twisted yarns. Weibull modules are different in different clamping gauges for the same acrylic self-twisted yarns. Weibull modules haveβmaximum value in 120 mm clamping the twisted gauge andηmaximum value in 110 mm clamping the twisted gauge. These two values correspond to the minimum discrete of the breaking strength and the maximum breaking strength average.
self-twisted yarns; breaking strength; Weibull distribution; clamping gauge; prediction
2014-01-06
肖志永(1979-),男,天津蓟县人,工程师,主要从事纺纱理论与工艺研究.
TS134.7
A
1674-330X(2014)01-0006-05
