旋耕埋草机螺旋横刀制造工艺误差及影响

张居敏，夏俊芳，张甜，张秀梅

(华中农业大学工学院，湖北 武汉 430070)

旋耕埋草机螺旋横刀制造工艺误差及影响

张居敏，夏俊芳*，张甜，张秀梅

(华中农业大学工学院，湖北 武汉 430070)

分析1GMC–70型船式旋耕埋草机核心耕作部件螺旋横刀的制造工艺过程，研究制造工艺误差量及对整机耕作性能的影响。结果发现，由于采用近似加工方式，致使螺旋横刀的旋转轴线与刀辊轴线构成了空间异面直线，两者之间垂直距离为204.2 mm，空间夹角为28.7°；螺旋横刀刃口上各点的旋转半径、静态滑切角和静态切土角等参数波动区间分别为[189.0，200.0]、[14.7°，32.4°]和[70.3°，73.7°]。螺旋横刀端部静态滑切角最小(14.7°)时，属于砍切范畴，导致耕作过程中端部刃口缠草；螺旋横刀端部刃口旋转半径最大(200.0 mm)时，静态切土角最大(73.7°)，这些因素影响整机单遍作业耕深。

旋耕埋草机；螺旋横刀；制造工艺；误差分析

1 横刀制造工艺过程分析

1.1 横刀结构

1GMC–70型船式旋耕埋草机刀辊结构[13]如图1–a所示，左、右旋横刀各5把，横刀刃口呈螺旋线，半径R=200.0 mm，螺距H=2 653.0 mm，螺旋升角为64.7°，刃口线上任意一点处的切线与刀轴之间的夹角(横刀静态滑切角)为25.3°，螺旋线两端绕刀辊轴线的转角为 46°。横刀沿刀轴方向的跨度为339.0 mm。横刀两端分别焊接在左、右弯刀上，刃口线长度为375.0 mm。横刀两端的正切面安装角为(17±2)°。图1–b表示图1–a中A–A截面的局部放大

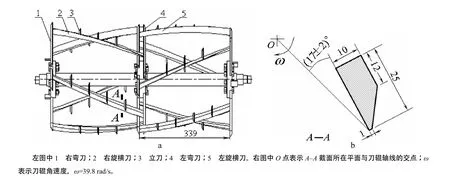
图1 刀辊结构Fig.1 Structure of the blade roller

1.2 工装夹具

以右旋横刀为例，工装夹具(图2)主要包括：钢管、三角钢板、夹具块和锁紧螺钉等。钢管长度400.0 mm，外径400.0 mm，管壁厚度30.0 mm。三角钢板焊接在钢管外圆柱面上，其焊接工艺过程为：第一步，加工一块平面直角三角形钢板 ABC(简称Rt⊿ABC)，厚度9.0 mm，∠C=64.7°，AB=400.0 mm；第二步，将Rt⊿ABC的AB边与钢管1圆柱体的1条母线紧密贴合并焊接；第三步，借助外力，使平面Rt⊿ABC变形，使其与钢管1的外圆柱面紧密贴合并焊接，这时AC边形成螺旋线，螺旋升角即 C∠与横刀刃口螺旋线升角相等。夹具块(宽度方向平行于它所覆盖的 AC边螺旋线段中点处的切线方向)宽度 40.0 mm，夹具块前后两底面分别焊接在Rt⊿ABC的外圆柱面和钢管1的外圆柱面上。

1.3 制造工艺

横刀制造过程分 3步：用 60钢加工成 375 mm×25 mm×10 mm的长方体；铣削其中1条长度为375 mm的棱边，使剩余横截面与横刀螺旋体截面相同，得到1个拉伸体；将拉伸体加热至红热塑性状态，插入夹具块3中，如图2所示，使厚度为10 mm的侧面与Rt⊿ABC的斜边AC(厚度9.0 mm)贴合，用锁紧螺钉固定拉伸体，分别沿钢管1径向和横刀斜面法向2个方向交替敲打刀体，使横刀宽度为25 mm的内表面与钢管1的外圆柱面密切贴合，同时厚度为10 mm的侧面与 ABCRtΔ 中斜边AC侧面密切贴合。松开锁紧螺钉，取出螺旋体结构的横刀。

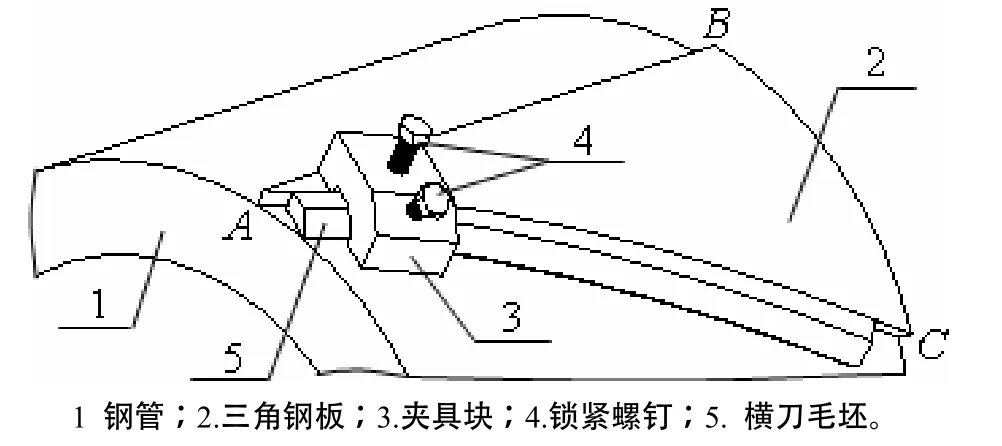
图2 横刀夹具Fig.2 Holding fixture of the helical blade

2 工艺误差分析

横刀两端分别焊接在左、右弯刀上，两端正切面安装角都为(17±2)°。考虑到横刀上述制造工艺过程，如果将正切面安装角(17±2)°改为90°，则横刀螺旋体的旋转轴线将与刀辊轴线重合。但实际上安装角只有(17±2)°，因此，横刀焊接后不再是绕刀辊轴线的螺旋体结构，其刃口线也不再是绕刀辊轴线的螺旋线，所以存在制造工艺误差。

2.1 确定现行工艺对应横刀主要棱边轮廓曲线方程

将图2中横刀端部结构放大，得到图3所示结构。过横刀刃口线①的起点D作垂直于刀辊轴线的平面，在平面与轴线交点处建立坐标系Oxyz，y轴沿刀轴方向，x轴经过D点，如图4所示(图3、图4中相同符号含义相同)。设横刀刃口线①的终点为E点，假设横刀两端面的安装角不是(17±2)°，而是90°，这时横刀是绕刀辊轴线的标准螺旋体结构，其各棱边在坐标系 Oxyz中都是标准螺旋线。让横刀绕直线 DE旋转，使两端面安装角从 90°变为(17±2)°。为确定旋转后横刀各棱边轮廓线的函数方程，需确定旋转前(安装角为90°时)主要棱边轮廓线①、②的曲线方程，再对坐标系 Oxyz进行平移、旋转等变换，并分析坐标变换过程中棱边轮廓线①、②对应曲线方程的变化情况。

图3 横刀夹具端部放大Fig.3 Enlarged detail of one end of the holding fixture of the helical blade

图4 坐标变换Fig.4 Coordinate conversion

为确定安装角，需要研究横刀棱边轮廓线①、②对应的函数方程。当安装角为 90°时，横刀内表面与半径为200.0 mm的圆柱体外壁密切贴合。设棱边曲线②与点O1所在平面(线段OO1长度为339 mm)交点为H点，刃口线①与点O1所在平面交点为 E，∠O1EH 被定义为横刀的端面安装角。∠O1EH =90°时，棱边轮廓线①在坐标系Oxyz中的方程为：

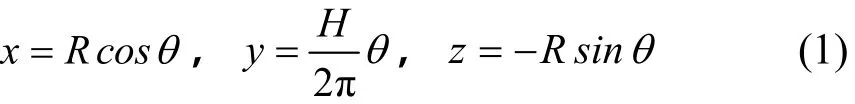
式中：R为螺旋半径， R =200.0 mm；H为螺距，H=2 653.0 mm。

当∠O1EH=90°时，为确定棱边曲线②在坐标系Oxyz中的方程，需要知道该曲线起点F的坐标。F在横刀螺旋体D端起始平面内，该平面与圆柱体底面之间的夹角等于横刀螺旋升角的余角，即为25.3°。在图4中，将坐标系Oxyz绕x轴负方向旋转角度θ0，θ0=25.3°，得到坐标系Ox0y0z0(图中只画出y0轴，没有画x0、z0轴，以下同)。在坐标系Ox0y0z0中，弧线段DF=25 mm，弧线段DF为椭圆的一部分，椭圆参数方程为：

弧线段DF长度为

由DF=25 mm，得θ1=6.475 1°，F在坐标系Ox0y0z0中的坐标为：

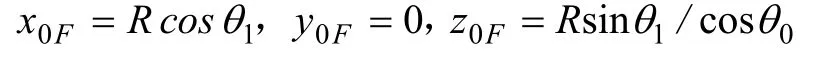
F在坐标系Oxyz中的坐标

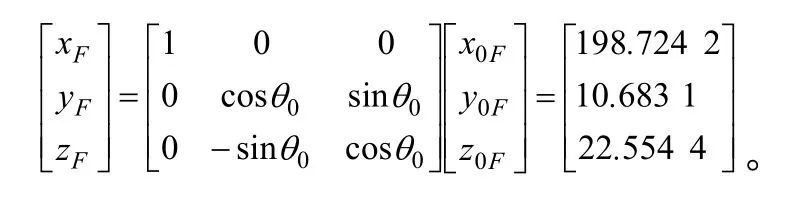
当∠O1EH =90°时，在坐标系Oxyz中，曲线②是标准螺旋线，它经过F，其参数方程为：

式中：Fθ为曲线②的初始位置角。

研究安装角为(17±2)°时横刀棱边轮廓曲线①、②在坐标系Oxyz中的方程，需要作4步坐标变换及逆变换，变化过程参考图4。

坐标变换1：将坐标系Oxyz沿x轴平移到D点，得到坐标系Dx1y1z1：

在坐标系Oxyz中，根据曲线①的参数方程(1)求出其终点E的坐标，E点参数θE=46°=0.802 9 rad。过E作直线垂直于坐标系Dx1y1z1中y1z1平面，垂足为G，G在坐标系Oxyz中坐标为：(R，339，–R sinθE)。设矢量DG与y1轴正方向之间夹角为12θ ，矢量DG、DE之间的夹角为23θ ，则有：

坐标变换2：将坐标系Dx1y1z1绕x1轴负方向旋转角度12θ ，得到坐标系Dx2y2z2，y2轴经过G点：

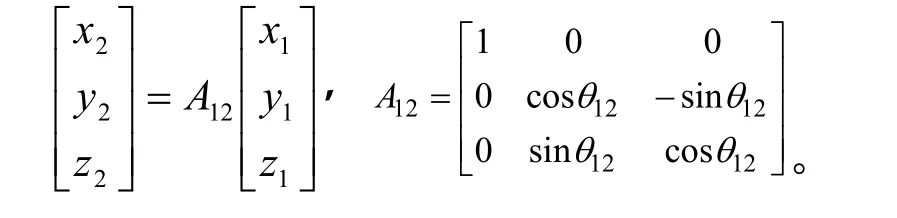
坐标变换3：将坐标系Dx2y2z2绕z2轴正方向旋转角度23θ ，得到坐标系Dx3y3z3，y3轴经过E点：

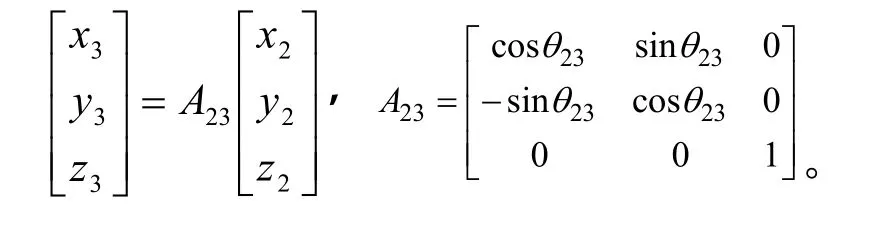
坐标变换4：将坐标系Dx3y3z3与安装角为90°的横刀固连在一起，然后将坐标系Dx3y3z3绕y3轴负方向旋转角度43θ (待定)，得到坐标系 Dx4y4z4，使得横刀E端面处的安装角由90°变为17°，两者之间关系为：

在坐标系Dx3y3z3、Dx4y4z4中，横刀各棱边轮廓曲线对应的方程相同。安装角为 90°时横刀棱边轮廓线①、②在坐标系 Oxyz中的参数方程依次如式(1)、(2)所示。通过上述4个步骤的坐标变换，求出这2条轮廓线在坐标系Dx4y4z4中的参数方程，再经过逆变换，即得出横刀安装角度为 17°时各棱边轮廓曲线在坐标系Oxyz中的参数方程。

曲线①的参数方程为：

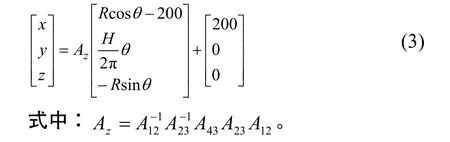
曲线②的参数方程为：

在方程(4)中，令y=339 mm，求出曲线②与O1平面交点 H的坐标，令∠O1EH=17°，求出43θ = 72.548 2°=1.266 2 rad。

横刀螺旋体结构的旋转轴线在安装角为 90°时与坐标系Oxyz的y轴重合，在安装角为17°时，该轴线在坐标系Oxyz的参数方程为：

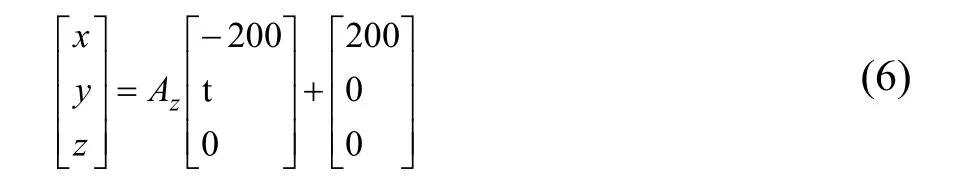
其中t为直线方程的参数。

2.2 主要旋耕参数计算分析

分析横刀两端安装角为(17±2)°时，其刃口曲线上各点处旋转半径、静态滑切角、安装角等沿刀辊轴线方向的变化规律；分析安装角为(17±2)° 时横刀螺旋体结构的旋转轴线与刀辊轴线之间的异面直线垂直距离。

2.2.1 横刀刃口曲线上各点的旋转半径

刃口曲线上各点处的旋转半径等于该点与刀辊轴线之间的垂直距离。将式(5)带入方程(3)，得到横刀刃口线①的参数方程，刃口上各点与刀辊轴线(y轴)之间的垂直距离为值和各点的y轴坐标值(参考图4，y轴坐标值表示横刀的轴向长度)都由方程(3)确定，它们都是参数θ的函数利用Matlab软件，绘制出r值与y轴坐标值之间的关系曲线(图5)。

图5 横刀刃口上各点的旋转半径Fig.5 Rotation radius for every point on the cutting edge of helical blade

2.2.2 横刀的静态滑切角

机组前进速度为0时，横刀刃口上某点的圆周速度矢量与该点刃口曲线法平面之间的夹角，称为该点的静态滑切角，静态滑切角等于速度矢量与刃口切线之间所夹锐角的余角[17]。横刀刃口曲线方程如式(3)所示，刃口曲线上任意一点处的圆周切线矢量坐标为：(z,0,–x)，其中 x、z由方程(3)确定。方程(3)对参数角θ求导数，得到曲线的切线矢量：

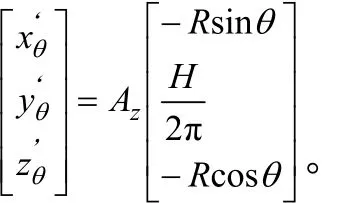
则静态滑切角为：

式中：τs是参数θ的函数，刃口曲线上各点的y轴坐标也是θ的函数，由Matlab软件可绘出横刀静态滑切角τs随y值(即横刀轴向长度)的变化规律曲线，如图6所示。

图6 横刀滑切角Fig.6 Sliding cutting angle of the helical blade

2.2.3 横刀任意位置处的安装角

在图4中，设圆柱体高度为y，并假设y为已知，则O1点坐标为(0，y，0)；E点坐标由方程(3)确定，θ由圆柱体高度y值确定；H点坐标由方程(4)确定，θ也由y值确定。点O1、E、H的坐标都是圆柱体高度y的函数，所以∠O1EH也是y的函数，由Matlab软件绘出安装角∠O1EH与y值即横刀轴向长度之间关系曲线，如图7所示。

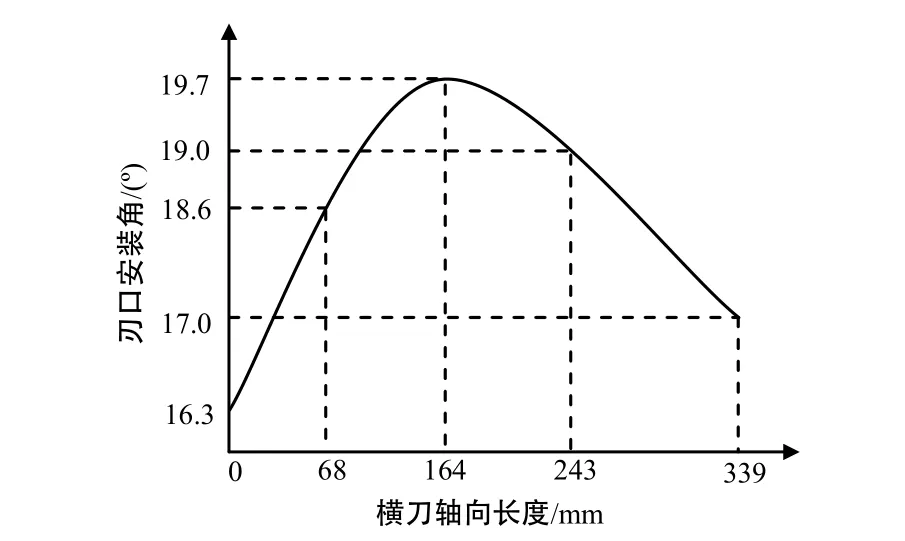
图7 横刀安装角Fig.7 Setting angle for the helical blade

2.2.4 横刀螺旋体结构旋转轴线与刀辊轴线之间空间异面直线的垂直距离

安装角为17°时，横刀螺旋体结构的旋转轴线在坐标系Oxyz中的参数方程如式(6)所示，该轴线与刀辊轴线构成空间异面直线，刀辊轴线在坐标系Oxyz中与y轴重合。用Matlab软件，计算出上述2条空间异面直线之间的最短距离为204.2 mm，最短距离发生在y=130.3 mm位置处，两直线之间的空间夹角为28.7°。

3 工艺分析过程的正确性检验

图8 横刀的三维装配模型Fig.8 Three-dimensional assembly model for the helical blade

为检验理论分析过程及由此产生的计算结果的正确性，用pro/e5.0软件对弯刀、刀盘、刀轴、横刀等进行三维造型，装配后如图8所示，其中横刀的三维造型按照横刀产品的制造工艺过程进行，其他零部件的三维造型按照设计图纸进行。图8中右旋横刀5在耕作过程中E端先切土，D端后切土。沿刀轴方向即y轴方向，设定不同y值，分别测量相应y值时三维模型中右旋横刀4的刃口与刀轴之间的垂直距离(r)、刃口静态滑切角(sτ)和安装角(∠O1EH)等，并与理论分析过程中相应公式计算结果(表1)相对比，以检验理论分析过程及结果的正确性

表1 参数的模型测量值与理论计算值的对比Table 1 Parameter values by model measurement and by theoretical calculation

从表1可知，横刀产品主要耕作参数的三维模型测量结果与理论分析计算结果相吻合，说明理论分析过程及结果正确。

4 工艺误差对刀辊耕作性能的影响

文献[11]详述了标准横刀的结构参数。标准横刀刃口上各点的旋转半径均为200 mm；横刀刃口上各点处的静态滑切角均为25.3°；横刀任意位置处的安装角均为18.3°；横刀任意位置处的静态切土角均为71.7°。经分析，现行工艺制造的横刀产品，刃口上各点的旋转半径在189～200 mm波动，这会造成刀辊耕深沿幅宽方向波动。

从图6可知，横刀刃口的静态滑切角在先入土一端较大(32.4°)；后入土一端较小(14.7°)，这会导致横刀沿入土顺序由滑切过渡为砍切。旋耕刀刃口与秸秆之间的摩擦角在 26°～45°[13–14]，标准横刀的静态滑切角为25.3°，但横刀产品的静态滑切角最小值仅为14.7°，远小于旋耕刀–秸秆之间的摩擦角下限，这属于砍切范畴[15–16]。在实际大田耕作过程中，横刀后入土一端存在缠草现象(图9)。横刀被背部焊接的立刀均匀分割为 4～5个独立的幅宽段落，先入土的幅宽段落因为滑切角比较大，属滑切范畴，所以不缠草，但最后入土的幅宽段落因为滑切角太小，属砍切范畴，所以缠草。砍切比滑切更费力[17–19]，在同样切削力情况下，砍切比滑切更难于切断秸秆，所以砍切部位有缠草现象。设横刀被立刀平均分割成5个独立段落，则每段长度约为68 mm，从图 6可知，横刀最后入土段的静态滑切角为14.7°～18.6°，整段范围内都属于砍切范畴。横刀缠草后刃口锋利程度下降，不利于入土、切土和秸秆切削等。

图9 横刀缠草分布Fig.9 Distribution of intertwined stubbles along helical blade

从图7可知，横刀安装角沿刀轴方向有波动。先入土一端安装角为 17°，后入土一端安装角为16.3°，两者不相等。横刀静态切土角等于安装角的余角，其后入土一端的静态切土角最大，为73.7° 而GB/T5669–1995规定IT245和IT260旋耕刀的静态切土角分别为40°和37.5°[20]。切土角增大，会增加切土阻力[21]，再考虑到后入土一端的静态滑切角最小(14.7°)，这说明横刀后入土一端的作业条件最差，既不利于土壤旋耕切土，也不利于秸秆切削。再考虑到横刀后入土一端旋转半径最大(200.0 mm)，这会降低整机单遍作业耕深。1GMC–70型船式旋耕埋草机单遍作业耕深较小，约为50 mm，这与横刀后入土一端的滑切角最小、切土角最大、旋转半径最大等因素有关。

5 结 论

由于工艺误差，横刀的螺旋体结构旋转轴线与刀辊轴线不重合，它们构成空间异面直线，其垂直距离为204.2 mm，空间夹角为28.7°。

现行工艺对应横刀产品的静态滑切角波动性较大。横刀先入土一端滑切角为32.4°，后入土一端滑切角为14.7°，耕作过程中刃口滑切角按横刀先后入土顺序由大变小，对秸秆切削方式由滑切过渡为砍切。横刀后入土一端滑切角偏小，存在砍切、缠草等问题。

横刀后入土一端滑切角最小、切土角最大、旋转半径最大，这些因素降低了整机单遍作业耕深。

[1] 张晓文，赵改宾，杨仁全，等．农作物秸秆在循环经济中的综合利用[J]．农业工程学报，2006，22(增刊1)：107–109．

[2] 姜洁，陈宏，赵秀兰．农作物秸秆改良土壤的方式与应用现状[J]．中国农学通报，2008，24(8)：420–423．

[3] 劳秀荣，吴子一，高燕春．长期秸秆还田改土培肥效应的研究[J]．农业工程学报，2002，18(2)：49–52．

[4] 高利伟，马林，张卫峰，等．中国作物秸秆养分资源数量估算及其利用状况[J]．农业工程学报，2009，25(7)：173–109．

[5] Pan Genxing，Zhou Ping，Li Zhipeng，et al．Combined inorganic/organic fertilization enhances N efficiency and increases rice productivity through organic carbon accumulation in a rice paddy from the Tai Lake region，China[J]．Agriculture，Ecosystems and Environment，2009，131：274–280．

[6] 张在平．旋耕埋草技术研究与试验[D]．武汉：华中农业大学工学院，2005．

[7] 许绮川，夏俊芳，张国忠，等．船式旋耕埋草机：中国，CN2896816[P]．2007–05–09．

[8] 夏俊芳，张国忠，许绮川，等．多熟制稻作区水田旋耕埋草机的结构与性能[J]．华中农业大学学报，2008 27(2)：331–334．

[9] 张国忠，许绮川，夏俊芳，等．1GMC–70型船式旋耕埋草机的设计[J]．农业机械学报，2008，39(10)：214–217．

[10] 姚兴林．基于虚拟仪器的螺旋型旋耕埋草刀辊转矩测试系统研究[D]．武汉：华中农业大学工学院，2010．

[11] 张居敏，周勇，夏俊芳，等．旋耕埋草机横刀的数学建模与参数分析[J]．农业工程学报，2013，29(1)：18–25

[12] 丁为民，彭嵩植．旋耕刀滑切角及滑切角方程的研究[J]．农业工程学报，1995，11(4)：67–72．

[13] 王福杰．IGLF–1.8型秸秆翻青机设计与研制[D]．武汉华中农业大学工学院，2011．

[14] You Yong，Wang Decheng，Liu Jude．A device for mechanical remediation of degraded grasslands[J]．Soil and Tillage Research，2012，118(1)：1–10．

[15] 寻怀义．滑切理论探讨[J]．农业机械学报，1979，10(4) 107–111．

[16] 刘洋．玉米青贮机滚筒式切碎装置的设计与有限元分析[D]．杨凌：西北农林科技大学，2008．

[17] 赵铁军，王金武．水稻秸秆整株还田埋草弯刀滑切角与安装角分析[J]．农机化研究，2007(11)：58–63．

[18] Damora D，Pandey K P．Evaluation of performance of furrow openers of combined seed and fertilizer drills[J]. Soil and Tillage Research，1995，34(1)：127–139．

[19] 冯佐龙．4QZ–12型青饲料收获机关键部件的研究[D]．保定：河北农业大学机电工程学院，2008．

[20] 中国农业机械化科学研究院．农业机械设计手册：上册[K]．北京：中国农业科学技术出版社，2007：236–237．

[21] 丁为民，王耀华，彭嵩植．反转旋耕刀正切面分析及参数选择[J]．农业机械学报，2004，35(4)：40–43．

责任编辑：罗慧敏

英文编辑：罗 维

Process errors in manufacturing helical blade for stubble burying rotary tiller and their influences on tillage

ZHANG Ju-min, XIA Jun-fang*, ZHANG Tian, ZHANG Xiu-mei
(College of Engineering, Huazhong Agricultural University, Wuhan 430074, China)

The manufacturing process of helical blades, the core tillage parts for boat-type 1GMC-70 stubble burying rotary tiller, was analyzed and the process errors and their influence on tillage performance were investigated. Results show that the approximation process used resulted in space straight lines on different planes formed by rotating axis of the helical blade and the blade roller, between which the vertical distance is 204.2 mm and space angle 28.7º. The rotary radii of points on helical blade leading edge, the static sliding cutting angles of helical blade and the static cutting angles of helical blade are ranging from 189.0 mm to 200.0 mm, 14.7º to 32.4º, 70.3º to 73.7º, respectively. Static sliding cutting angle on the end of the helical blade is the smallest, which is 14.7º and belongs to cutting mode, resulting in stubble winding on the end of the blade during tillage. Rotary radius and static cutting angle on the end of helical blade are both the largest, which are 200.0 mm and 73.7º correspondingly. These factors influence the tillage depth of the tiller in a single performance.

stubble burying rotary tiller; helical blade; error analysis

10.13331/j.cnki.jhau.2014.01.019

时间：2014– – 00:00

网络出版地址：

S222

A

1007−1032(2014)01−0091−07

秸秆还田既能解决农业废弃物处理的难题，又能减少化肥施用量，增加土壤有机质含量，保持土地肥力[1–5]。1GMC–70型船式旋耕埋草机技术相对成熟，对水田高茬秸秆埋覆还田的作业效果已经得到市场认可[6–10]。螺旋横刀(简称横刀)是该机核心耕作部件，为螺旋体结构，机械加工难度较大，为便于大批量生产，一般采用近似加工方式。笔者分析横刀制造工艺误差量及其对作业效果产生的影响，以期为工艺改进及优化提供理论参考依据。

2013–09–23

国家自然科学基金项目(51275196)；公益性行业(农业)科研专项(201203059)

张居敏(1972—)，男，河南南召人，博士研究生，讲师，主要从事秸秆禁烧、土壤耕作研究，ju_min_zhang@mail.hzau.edu.cn

*通信作者，xjf@mail.hzau.edu.cn