电磁风扇离合器系统参数匹配设计

袁 恒，马 力，张 望

（武汉理工大学 汽车工程学院，武汉430070）

电磁风扇离合器系统参数匹配设计

袁 恒，马 力，张 望

（武汉理工大学 汽车工程学院，武汉430070）

分析电磁风扇离合器系统振动问题及影响因子，进行影响因子灵敏度分析，从而拟定灵敏度计算公式。提出了电磁风扇离合器系统参数匹配设计方法和技术路线，并针对典型风扇离合器系统进行参数匹配设计。不仅解决原结构振动过大问题，还保证结构柔性损失小，使系统质量有所降低，取得了很好的效果。

振动与波；汽车；电磁风扇离合器系统；灵敏度分析；参数匹配设计

典型电磁风扇离合器系统由电磁风扇离合器和减振法兰盘组成，结构如图1所示。工作时，法兰盘通过螺栓连接到发动机皮带盘上，转矩经过法兰盘传到电磁风扇离合器。

目前，工程实践和有关研究[1,2]工作表明，振动过大的原因为系统弯曲振动固有频率未有效避开电磁风扇离合器工作的激励频率。如果将图1所示的电磁风扇离合器1考虑为具有质量和转动惯量的刚体，则可将系统简化成图2所示模型，图中r为电磁风扇离合器质心到减振法兰盘2安装平面的距离。

定义法兰盘安装平面上且通过中心点的水平轴为L1，与其平行且通过电磁风扇离合器质心的轴为L2。若设m为电磁风扇离合器的质量，K为减振法兰盘的弯曲刚度，J为电磁风扇离合器关于L1轴的转动惯量，J0为电磁风扇离合器关于L2轴的转动惯量，则系统的弯曲振动固有频率为

式中J的大小为

显然，影响电磁风扇离合器系统弯曲振动固有频率的因子有K、J0、m和r。匹配这些因子使法兰盘具有足够的弯曲刚度、系统振动小、质量轻、减振柔性好是系统参数匹配设计考虑的主要问题。

图1 电磁风扇离合器系统结构

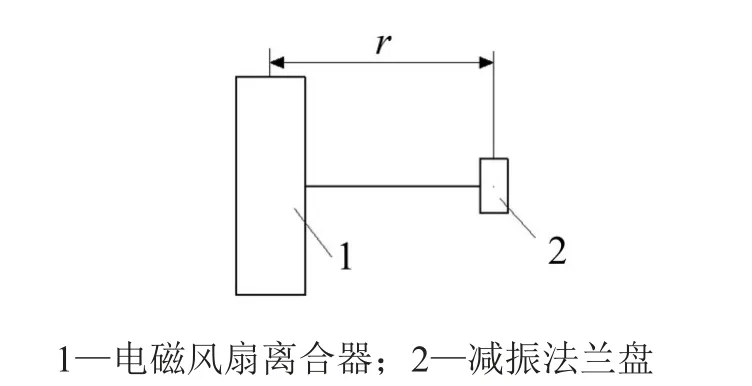
图2 电磁风扇离合器系统简图

2 影响因子灵敏度分析

灵敏度分析是研究系统的输出变量对影响因子变化的敏感程度，其数值的大小可以反映出影响因子对系统性能的影响情况。可根据灵敏度分析结果，选择合适的影响因子对结构进行参数匹配或者优化设计。

设X、Y和Z分别为法兰盘弯曲刚度K、电磁风扇离合器转动惯量J0和质量m的影响因子，则可将K、J0和m分别看作X、Y和Z的函数，记为K=K（X)、J0=J0(Y)和m=m(Z)。因此，系统弯曲振动固有频率函数为

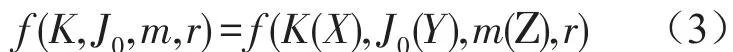
上式分别对变量X、Y、Z和r求偏导，可得

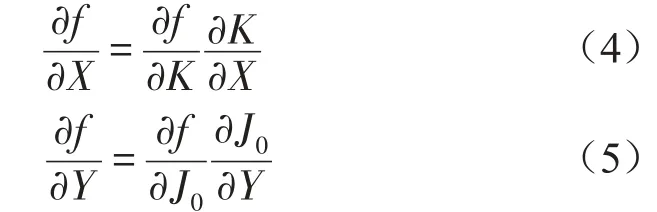
对于电磁风扇离合器系统，若能把所有影响因子K、J0、m、r、X、Y和Z进行匹配设计，将是最理想的匹配方案。但影响因子X、Y和Z是前期研发和生产电磁风扇离合器及法兰盘时要考虑的问题，本项目只需要对现成的电磁风扇离合器和法兰盘进行匹配，所以不用考虑因子X、Y和Z的影响。因此，电磁风扇离合器系统的参数匹配设计因子是K、J0、m和r，则式（4）—式（7）可简化为

将式（1）、式（2）代入式（8）—式（11），可得系统弯曲振动固有频率f对变量因子K、J0、m和r的灵敏度值分别为

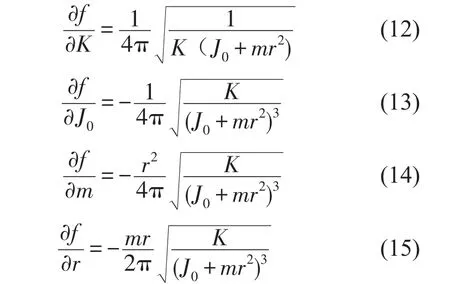
其结果分别如图3中（1）—（4）所示。

图3表明，系统弯曲振动固有频率对参数因子r的变化最敏感。所以，选择参数因子r和其他因子进行匹配设计是最有效的。因为参数因子J0与电磁风扇离合器的质量分布有关，要改变J0必须重新设计风扇离合器，操作十分麻烦。对于参数因子m，可通过使用新材料或改进结构使之减小，但却需要进行大量试验研究，耗费时间和成本。因此，选择参数因子r和K进行匹配设计是最方便的。

3 参数匹配设计技术路线

由式（1）和式（2）知，提高系统弯曲振动固有频率使之大于系统上限工作频率的方法是减小参数因子r，并控制K，使K不变或者稍微提高。

法兰盘结构如图4所示，由外套、内套和减振元件组成，其弯曲刚度K是由结构和材料所占比例关系决定的。其中减振元件采用橡胶，外套和内套采用金属材料制成。外套和内套具有连接和支撑作用，减振元件起到扭转减振的作用。在特定结构中，法兰盘的弯曲刚度K、质量和减振柔性跟金属材料和非金属材料的比例有关。定义比例系数ξ=m1/m2，式中m1和m2分别为法兰盘结构中金属材料和非金属材料的质量。一般来说，ξ值越大，金属材料比重大，则法兰盘的弯曲刚度大，质量大，柔性差；反之，ξ值越小，非金属材料比重大，法兰盘的弯曲刚度较小，质量轻，柔性好。

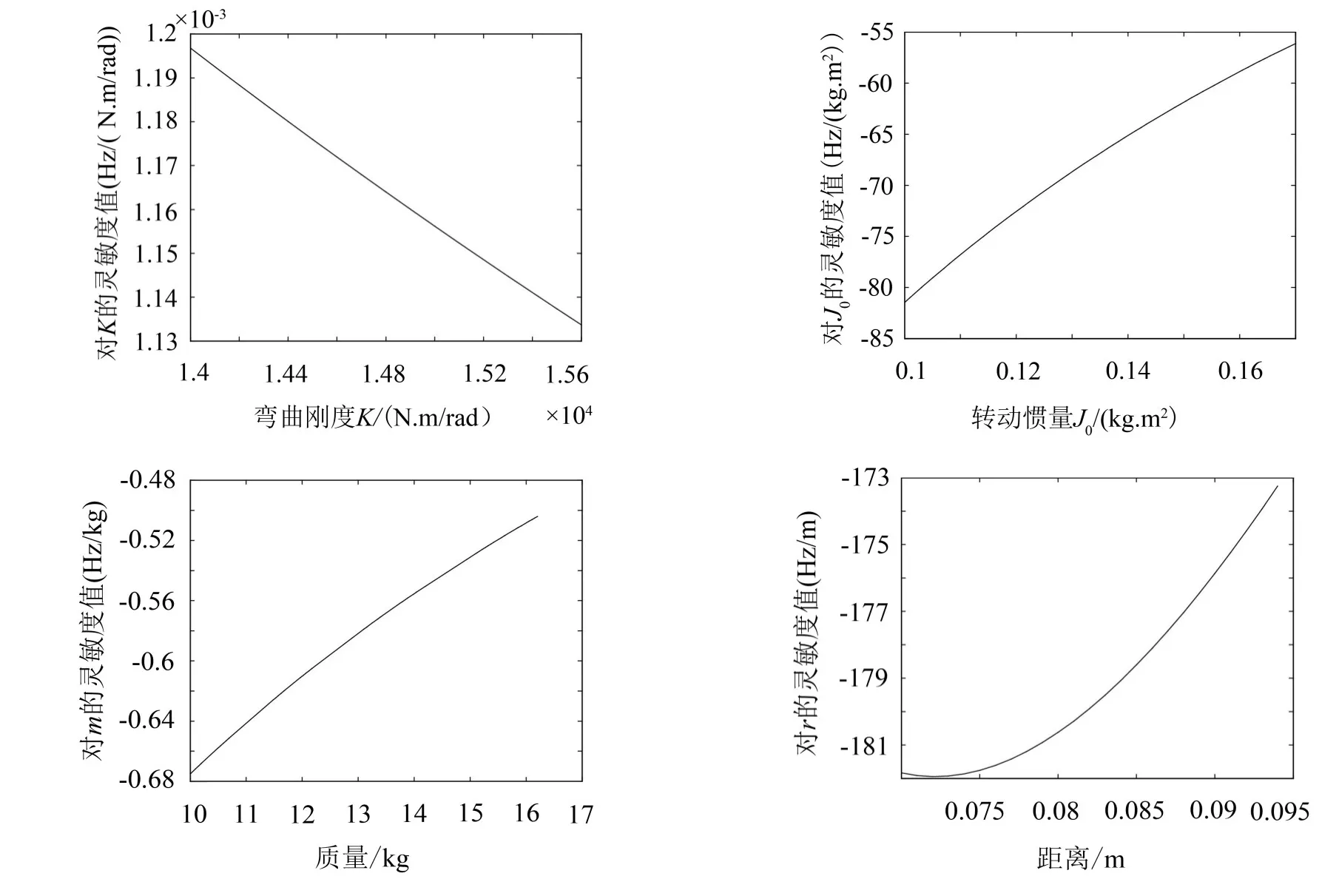
图3 系统弯曲振动固有频率对因子K、J0、m和r的灵敏度

减小r的方法是使电磁风扇离合器的质心向法兰盘方向移动。设质心移动距离为ΔL，质心移动原理如图5所示。其中图a)是原结构示意图；图b)是将如图1所示的间距L缩短，则质心随之偏移；图c)是保持电磁风扇离合器相对法兰盘位置不变，而将其质量大小不同的部件进行位置调整，使质量大的部件安装在靠近法兰盘的位置，从而使质心向法兰盘移动；图d)是结合使用图b)和图c)所述方法，使得质心向法兰盘移动更大距离。在这四种质心移动方法中，第二种最便于实施，所以在本研究中使用。

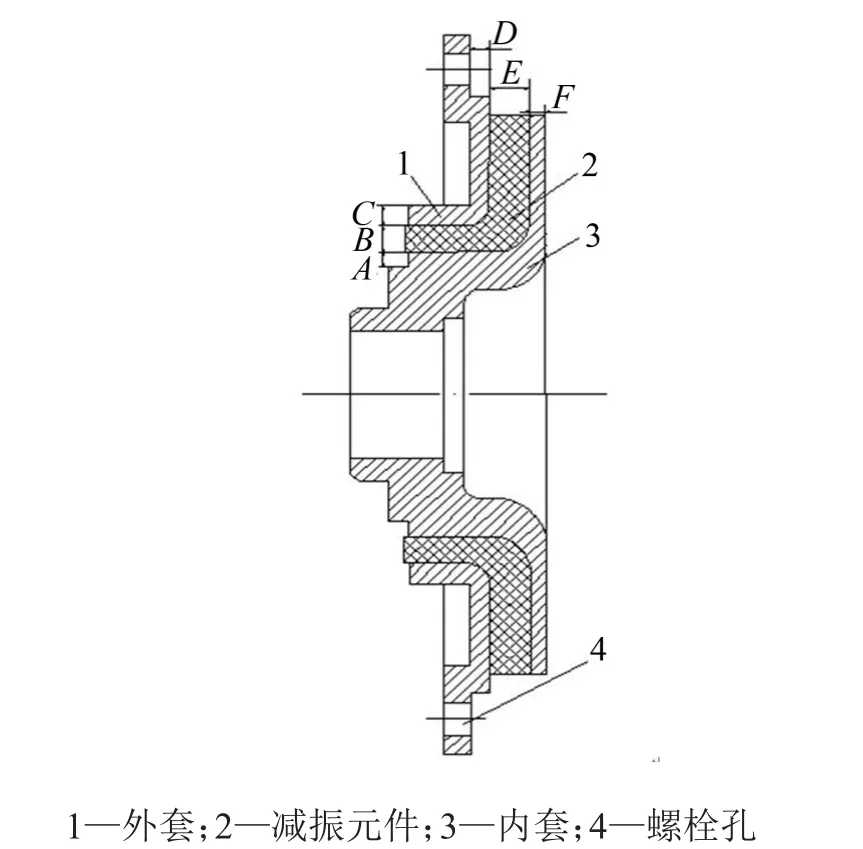
图4 法兰盘结构

图5 质心移动原理

设r0和r1分别为原结构和新结构中法兰盘安装平面到风扇离合器质心的距离，J1为新结构关于L1轴的转动惯量，f1为电磁风扇离合器的上限工作频率，Kmin和Kmax分别为法兰盘弯曲刚度要求的上下限值；定义XP、K(XP)和M(XP)分别为法兰盘优化设计的设计变量、弯曲刚度函数和质量函数。因此，电磁风扇离合器系统参数匹配设计的技术路线如图6所示。图中,Kmin和Kmax可根据法兰盘的工作转速要求及电磁风扇离合器的转动惯量来确定，在典型产品设计中也可以由初始结构刚度K0乘上系数来估算。一般情况下，Kmin越大，系统的稳定转速越高，但是过大会导致减振柔性下降和结构质量上升，因此用Kmax来控制设计容差。

图6 电磁风扇离合器系统参数匹配设计技术路线

4 典例分析

某企业提供的电磁风扇离合器要求的工作转速是800 r/m in～2 400 r/m in。试验和实际应用表明，当发动机的驱动转速约为2 000 r/m in时，系统出现共振现象，从而导致电磁风扇离合器不能正常工作甚至损坏。现用所提出的方法进行匹配设计。

4.1 系统参数匹配设计的实现

根据原系统各部件安装位置情况，在保证电磁风扇离合器不与法兰盘发生干涉情况下，将L缩短0.006 m，从而使电磁风扇离合器质心向法兰盘偏移0.006 m。由企业提供的原结构相关数据，可得r1为0.088 6 m。从而计算出J1和Kmin分别为0.298 kg.m2和188 04.23 N.m/rad。

法兰盘的结构参数如图4所示，以图中参数A、B、C、D、E和F为设计参数对法兰盘进行参数化建模，结构的弯曲刚度K和质量M跟这些参数有关，但很难通过显式函数表达。参数匹配时通过数值计算来实现，这可由有限元系统相应计算功能来完成。图7为优化匹配模型，当前参数下结构的质量可由有限元系统直接获取，法兰盘的弯曲刚度为轴1-2端点处的力偶与轴相应转角的比值。在线性小变形情况下，转角可由轴两个端点处的位移依据正切角和微小转角的近似线性关系算出。计算时在法兰盘与发动机皮带盘螺栓连接孔位处施加位移约束。

设XP={A，B，C，D，E，F}、K(XP)和M(XP)分别为法兰盘优化设计的自变量、状态变量和目标函数。最后，采用子问题逼近法对法兰盘模型进行优化匹配设计。匹配迭代时，参数A、B、C、D、E和F必须满足其上下限约束要求，具体值如表1所示，这些值可通过试算获取或者和企业设计人员商定。

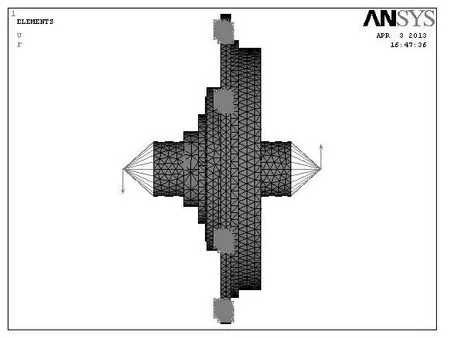
图7 法兰盘优化匹配模型

4.2 参数匹配设计结果分析

系统参数匹配设计的计算结果如表1所示。法兰盘弯曲刚度为21 500 N.m/rad,扭转刚度为3 810 N.m/rad，结构的弯曲振动固有频率为42.77 Hz，使安全工作范围可达2 566 r/m in，满足电磁风扇离合器的工作转速范围800 r/m in～2 400 r/m in要求。与传统改进方法得到的研究结果相比[3]，在保证同样工作转速要求下，法兰盘弯曲刚度下降56.12%，扭转刚度下降37.73%，减振柔性更好。另外，匹配设计结果使法兰盘质量较原结构下降19.57%。显然，系统参数匹配设计更有优势。

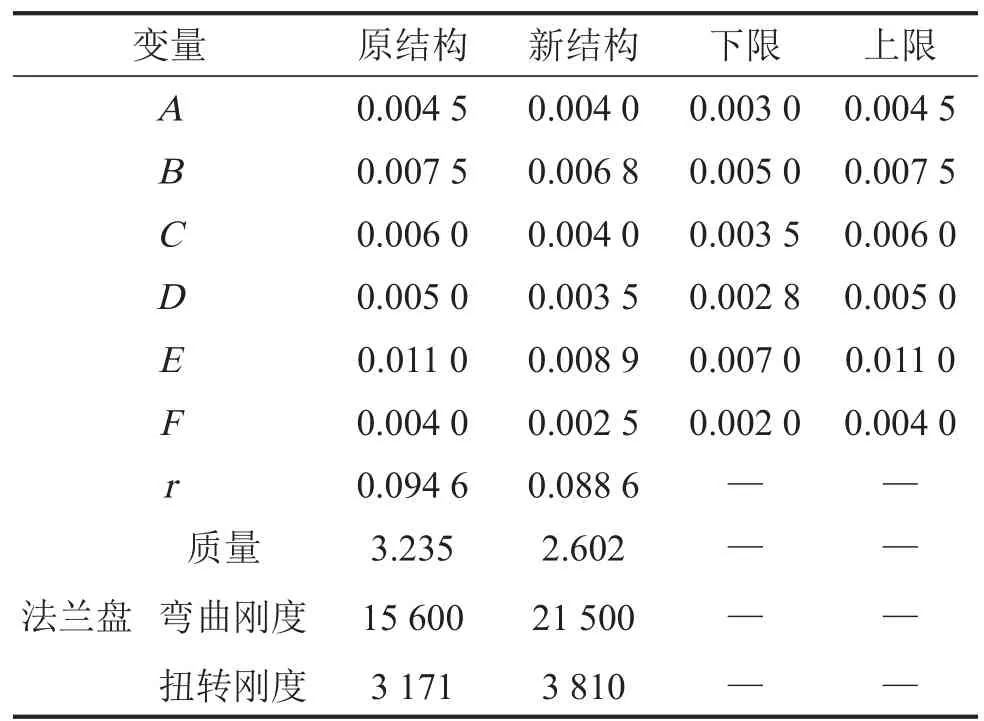
表1 参数匹配设计结果（N，kg，m，rad）

5 结语

计算、对比和分析表明系统参数匹配设计是成功的。新结构不仅能解决系统振动过大问题，还能使系统工作更加柔和平顺，保持较好的减振柔性，噪声小，减振作用良好。

提出的电磁风扇离合器系统参数匹配设计方法应用范围广，便于实施，能够指导各种不同结构的电磁风扇离合器进行系统参数匹配设计，利于提高产品设计水平。系统振动问题[J].汽车工程师，2012，（02）：29-31.

[4]杜媛媛，马 力，王 翠.基于APDL的柔性减振法兰盘的参数化设计[J].研究与开发，2011，（10）：73-76.

[5]孙秋凤，马 力，王 翠.电磁风扇离合器减振法兰盘的改进设计[J].上海汽车，2011，（10）：28-30.

[6]邓江华，刘献栋，李兴虎，单颖春.车身阻尼层结构的声灵敏度分析及优化[J].噪声与振动控制，2009，（01）：54-57.

[7]马 迅，过学迅，赵幼平，闵晓炜.基于有限元法的结构优化与灵敏度分析[J].

[1]刘文杰，马 力，张中正.基于ABAQUS的电磁风扇离合器模态分析[J].机械科学与技术，2002，（04）：558-561.

[8]张 武，陈 剑，陈 鸣.采用正交试验的发动机悬置系统灵敏度分析[J].专用汽车，2012，（01）：89-90.

[2]张中正，马 力，梁文英.应用ADAMS分析解决电磁风扇离合器振动[J].现代零部件，2011，（09）：64-65.

[3]王 翠，马 力，刘兴敏.汽车发动机电磁风扇离合器噪声与振动控制，2011，（05）：168-172.

Parameter Matching Design for Clutch System of an Electromagnetic Fan

YUAN Heng,MA Li,ZHANG Wang

(Institute ofAutomobile Engineering,Wuhan University of Technology,Wuhan 430070,China)

Vibration problem of the clutch system of an electromagnetic fan is analyzed.Sensitivity of the impact factors of the clutch sytem are studied,and the sensitivity formulae are worked out.Then,the design method and technical route of parameter matching for the clutch system are presented.The parameters matching design is done for the clutch system of a typical electromagnetic fan.Research result shows that the parameter matching design can solve the excessive vibration problem of the system,ensure the good flexibility of the structure and reduce the weight of the system.

vibration and wave;automobile;electromagnetic fan clutch system;sensitivity analysis;parameter matching design

1006-1355(2014)04-0161-04+168

TB53；U464.138+.4 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.035

振动过大是电磁风扇离合器系统匹配设计过程中常见的问题。目前对这个问题的研究主要集中在系统的动力特性分析[1—3]、法兰盘改进设计和参数化设计等方面[4,5]，虽然研究解决了典型系统振动过大的问题，但是却没有综合考虑系统的质量参数、转动惯量、尺寸参数、结构刚度和减振柔性匹配设计问题。另一方面，目前车辆结构设计灵敏度分析有许多有价值的研究[6—8]，但在电磁风扇离合器系统参数灵敏度分析及匹配设计方面的工作，还未见报道。

因此，进行电磁风扇离合器系统振动问题及影响因子分析，研究各影响因子灵敏度问题，提出系统参数匹配设计技术路线并进行匹配设计就显得非常重要。围绕这些方面进行了分析研究，通过实践不仅解决了具体产品振动过大问题，还为提高新产品的自主研发能力和设计水平提供了有效的参考。

1 振动问题及影响因子分析

2013-12-13

袁 恒（1988-），男，广西河池市人，硕士研究生，研究方向：汽车计算机辅助设计。

马 力，男，硕士生导师。

E-mail:qichecad@126.com。