单向加筋双层板隔声性能的有限元分析

王义柏，魏智平，郑 辉,2

（1.上海交通大学 汽车工程研究院，上海200240；2.上海交通大学 振动、冲击、噪声研究所，上海200240）

单向加筋双层板隔声性能的有限元分析

王义柏1，魏智平1，郑 辉1,2

（1.上海交通大学 汽车工程研究院，上海200240；2.上海交通大学 振动、冲击、噪声研究所，上海200240）

为考察筋板声学透明假设理论对于加筋双层板隔声计算的适用性，对典型波纹芯体加筋双层板在简谐平面声波正入射和斜入射激励下的声透射损失（STL）进行有限元分析。分别建立筋板声学透明声腔和结构-声学全耦合加筋双层板的有限元模型，计算得到结构具有不同芯体构型和腔内声学介质时的STL曲线。结果表明，筋板“声学透明”假设模型带给加筋双层板STL计算误差取决于筋板结构阻抗和筋板间腔内介质声阻抗相对大小。因此，加筋双层板结构STL的准确预测需考虑筋板与腔内介质间与的结构-声学耦合作用。

振动与波；加筋双层板；声透射损失；结构—声学耦合；有限元分析

针对金属双层加筋板结构的声透射问题，许多学者开展了大量的理论、数值和实验研究工作。辛锋先和D’A lessandro等人对这一领域的研究工作进行了较全面的综述[1，2]。其中金属加筋夹层板隔声问题的理论研究方面，广泛采用Mead等人提出的针对空间周期结构的空间谐波法[3，4]进行分析建模，并考虑腔内声学介质与上下面板的声—固耦合作用，建立矩形、三角形筋双层板结构的声透射损失计算模型。变参数计算结构表明，由于筋板的连接作用，加筋双层板的隔声量变化在低频域和高频域表现不同趋势，并与筋板几何尺寸相关。基于空间谐波法的周期结构声透射计算模型随后被用来求解中间填充泡末吸声材料的正交加筋双层板结构的隔声问题[5]。

然而，现有的加筋双层板声透射问题的理论模型大多对筋板结构进行了简化，如简化成刚性体或平移/转动弹簧等[4]。另一方面，这些对夹层板的声透射问题建模时假设中间筋板声学透明，即忽略筋板对空腔的间隔作用，两面板之间的各个声学空腔当作是连通的。Brunskog专门研究了有限空腔对双层结构隔声的影响，发现连通空腔的假设并不完全符合夹层板的声透射实际情形[6]。但Brunskog的理论模型并未考虑筋板与面板—筋板闭合声腔的结构—声学耦合机制。

本文旨在探究筋板“声学透明”假设对加筋双层板结构隔声计算带来的影响。考虑筋板的分割声腔作用及筋板与闭合空腔间的结构—声学耦合，加筋双层板的声透射问题便成为多声腔的结构—声学耦合问题。为此，建立双层加筋板声透射损失计算的两类不同有限元模型，即“筋板声学透明模型”和“全耦合模型”。其中全耦合模型不仅考虑双层加筋板的面板与其间声腔的结构—声学耦合，还考虑筋板与声腔介质的结构—声学耦合作用；而筋板声学透明模型不考虑芯体筋板对面板间声腔的分割作用，忽略筋板与声腔介质的结构—声学耦合。分析对象为具有典型波纹芯体构形（矩形/梯形）的铝质加筋双层板，用建立的有限元隔声计算模型分别计算平面简谐正入射和斜入射条件下以及加筋双层板不同声腔介质（空气/水）时结构的声透射损失（STL），并比较两类不同模型计算得到的声透射损失结果以分析筋板“声学透明”假设的适用条件。

1 声透射问题的有限元分析建模方法

1.1 有限元模型的建立

对于声透射问题的有限元计算有多款较为成熟的商用软件可供选择，如ANSYS，ACTRAN等[9，10]。本文选用ABAQUS软件进行单向加筋板的隔声计算。

因为分析主要针对波纹芯体通过钎焊与上下面板连接的铝质双层板，属单向加筋双层板结构，为了减小求解规模，建立二维有限元模型，求解该结构—声学耦合系统在不同频率平面声波激励下的稳态响应(Steady State Response)。

用ABAQUS建立的加筋板声透射分析的有限元模型如图1所示。在加筋双层板的入射侧面板定义声学激励，即平面入射声波（Incident plan wave）。由于声—固耦合关系，入射平面声波将激起结构的前面板、筋板和声腔、后面板的振动，最终引起透射侧外声场的声学响应。将加筋双层板与声学域（入射侧和透射侧外声场及内声腔）在接触面上绑定约束(Tie constraint)，用以模拟结构与流体介质的耦合。加筋双层板的透射侧外声场实际是一个半无限大声学域。作为近似，在有限元模型中取一个足够大的半圆形声学域，并将其弧形边界设置成不反射阻抗边界(Non-reflection impedance)。

图1 ABAQUS中的加筋板声透射有限元模型

上式表明：若待求解的频域很宽，有限元模型将规模庞大，求解非常困难。为此，本文采用分频段模型，将待求解的全频段分割成4个相接的较小频段，针对每个小频段建立一个相应的有限元模型求解，最后将各小段声学响应结果综合在一起得到全频段声学响应。

所考虑的加筋双层板有两种芯体几何结构：(a)直筋双层板，分割上下面板中间的空间为20个矩形小声腔；(b)梯形筋双层板，分割两面板之间的空间为20个梯形小声腔。见图2所示。

在有限元模型中，声学域的材料为空气，密度ρf=1.11 kg/m3，体积模量Kf=1.35×106Pa；采用二次声学单元AC2D 8划分声学介质网格。结构材料为铝，密度ρ=2 700 kg/m3,杨氏模量E=7.1×1010Pa,泊松比ν=0.33；采用二次平面应变单元CPE8R划分结

为了可靠地模拟半无限大声学域，半圆形外声场的半径R1必须不小于1.5倍的最大声波长[7]。同时，对内、外声学域划分网格必须足够密，使得一个声波长内至少有6个～10个单元。为提高声透射损失的计算精度，此处采用更严格的网格划分标准建立有限元模型，即

其中d是声学域网格的最大尺寸，λmin和λmax分别是最高分析频率和最低分析频率所对应的声波波长。

通过估算半圆形透射声学域的网格数N来估计整个声学有限元问题的规模构单元。

图2 两类加筋双层板的几何结构

1.2 加筋双层板的声腔内结构—声学耦合

为了研究筋板与声腔介质间结构—声学耦合对加筋板结构声透射的影响，建立采用建立三类不同内耦合关系的有限元模型：(a)真空声腔模型：两面板之间的介质与面板、筋板都不设置内耦合约束。采用该模型所求得的声透射损失完全是结构传声的结果；(b)筋板“声学透明”腔模型，如图3(a)所示。两面板间的声学介质相通，与筋板无耦合作用，只与上下两面板耦合；(c)全耦合声腔模型，如图2(b)所示。两面板间的声学介质被筋板分割成多个小声腔，每个小声腔与上下面板、左右筋板分别耦合。

图3 筋板“声学透明”模型和全耦合模型示意图

1.3 有限元分析结果后处理

在透射声场中提取包围结构辐射面一周的声压响应(POR)数据，计算透射声功率（参见图4）

其中θ是对应声压观测点的极角，ρfc0是辐射声场中的声学介质阻抗。

在简谐平面声波激励下，入射声功率为

其中φ是声波入射角。

于是得到结构在激励频率f/Hz时的声透射损失(STL)为

1.4 有限元模型的验证：简支梁的声透射

作为对上述有限元分析模型的验证，先以此求解简支梁的STL，并与理论结果作比较。

如图4如示，简支梁为铝质材料，长L=1 m，厚h=5 mm，材料结构阻尼系数η=0.1；平面声波正入射，即φ=0°。

图4 简支梁声透射问题理论模型

求解简支梁STL的理论结果时，先用模态分解法求梁在声激励下的位移响应，再采用Rayleigh积分得到梁向半自由空间的辐射声压[8]。最后根据(3)—(5)式求得STL的理论解。

图5为简支梁STL曲线的有限元计算结果和理论解对比。结果表明，两种解法求得的隔声曲线十分吻合。因此采用前述有限元分析建模方法求解加筋双层板结构的声透射问题是可靠的。

图5 简支梁STL：有限元解和理论解比较

2.有限元分析结果及讨论

针对两种波纹芯体筋板形式（直筋和梯形筋）的双层板，分别考虑不同筋板/面板厚度、平面声波入射角度和声腔介质三种因素条件，用筋板“声学透明”模型和“全耦合”模型计算得到STL结果的差异。

2.1 厚加筋双层板

取模型参数：（1）加筋双层板的长度L=1 m，板间距为H=28 mm，面板和筋板厚度为h1=h2=2 mm，梯形筋板的倾角为β=60°；(2)双层板的材料结构阻尼η=0.1；(3)正入射平面声波激励，即φ=0°。用上述有限元建模方法建立加筋双层板的声透射分析模型，分别计算直筋双层板、梯形筋双层板在真空腔、声学透明腔和全耦合腔时的STL，结果见图6。

由图6可见，对较厚的双层板结构，不论是筋的形式如何，采用筋板“声学透明”假设模型得到的隔声曲线与全耦合模型得到的隔声曲线几乎完全一致，并且都与用真空腔模型得到的隔声曲线吻合。这是因为比较厚的加筋双层板结构，其结构阻抗远大于腔内空气的声学阻抗，其结构传声占主导，空腔与筋板的结构—声学耦合作用基本可以忽略，此时采用筋板“声学透明”假设得到的隔声结果足够精确。

2.2 薄加筋双层板

取模型参数：(1)L=1 m，H=56 mm，h1=h2=0.5 mm，β=60°；(2)双层板的结构阻尼η=0.005；(3)正入射声波激励，φ=0°。计算得到的直筋双层板、梯形筋双层板在真空腔、筋板“声学透明”腔和全耦合腔时的STL结果见图7。

图7给出的结果表明，对较薄的双层板结构，三种内耦合条件的隔声曲线有差异。相对而言，直筋双层板在三种情况下的隔声量差异较小，这与较厚双层板类似。而梯形筋双层板三种情况下的隔声量差异较大：在低频段，筋板“声学透明”腔模型得到的隔声曲线与真空腔模型的隔声曲线一致，都与全耦合模型的隔声曲线有一恒定差异；中频段，三条隔声曲线共振点有偏移；高频段，三者的差异较小。

平面声波斜入射激励，即φ=60°时，分别用筋板“声学透明”腔模型和全耦合腔模型计算直筋双层板、梯形筋双层板的STL，结果如图8所示。

图8(a)结果表明，在斜入射平面声波激励下，即使对于直筋双层板，用筋板“声学透明”声腔模型计算得到的隔声曲线与全耦合声腔模型得到的隔声曲线也存在较大差异。对两类不同芯体的双层板结构，其筋板“声学透明”声腔模型得到的隔声曲线出现了许多用全耦合声腔模型计算得到的隔声曲线中所没有的谷点。

图7和图8的结果说明了对于比较薄的加筋双层板结构，筋板“声学透明”假设带来的STL计算误差与芯体结构的拓扑形状和激励声波入射角有关。相对于正入射激励条件下的直筋双层板结构的隔声量计算，筋板“声学透明”假设给斜入射条件下梯形筋双层板结构的隔声量计算带来较大误差。

图6 较厚双层板在正入射平面声波激励下的隔声曲线

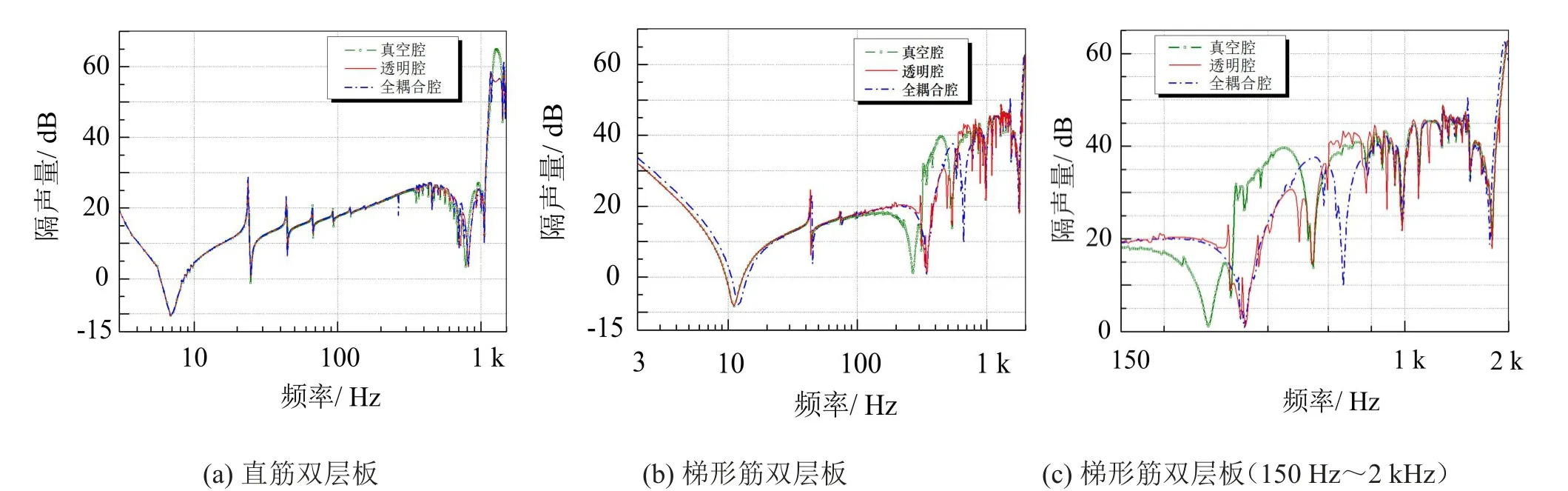
图7 较薄双层板在正入射平面声波激励下的隔声曲线

图8 较薄双层板在斜入射平面声波激励下的隔声曲线

2.3 声腔介质的影响

把上述厚梯形筋双层板结构的声腔介质以水（密度ρf=1 000 kg/m3，体积模量Kf=2.2 E9 Pa）取代空气，分别用筋板“声学透明”腔模型和全耦合声腔模型计算正入射平面声波激励下的STL，结果见图9。在水介质声腔条件下，较厚的梯形筋双层板的“透明声腔”模型得到的STL曲线与全耦合声腔模型得到的结果也存在较大差别，主要体现在低频段，频率增大后两条曲线趋于一致。这一结果与较薄的梯形筋双层板在空气声腔条件下所得到的结果类似。这是因为如果加筋双层板结构的声腔充满了重介质，腔内流体的声阻抗与结构的声学阻抗可以比拟。此时若采用筋板“声学透明”假设将给加筋双层板结构的隔声计算带来较大误差。

图9 声腔介质为水时厚梯形筋双层板的隔声曲线

3 结语

在加筋双层板振动—声学分析中广泛采用的筋板“声学透明”假设存在适用范围的局限性，给双层板结构的声透射损失计算带来的误差取决于芯体筋板的结构阻抗及面板间腔内声学介质的声学阻抗。对于比较薄的结构，或者结构腔体中充满重介质的应用场合，筋板“声学透明”假设不再适用。为得到加筋双层板结构声透射损失较精确计算结果，必须考虑筋板对声腔的分隔和筋板与面板-筋板闭合声腔间的结构—声学耦合机制。

[1]辛锋先，张钱城，卢天健.轻质夹层材料的制备和振动声学性能[J].力学进展，2010，40(4)：375-399.

[2]辛锋先，卢天健，陈常青.轻质金属三明治板的隔声性能研究[J].声学学报(中文版)，2008，33(4)：340-347.

[3]D.J.Mead and K.K.Pujara.Space-harmonic analysis of periodically supported beams:response to converted random loading[J].Journal of Sound&Vibration,1971, 14:525-532.

[4]LEE J.H.,KIM J.Analysis of sound transmission through periodically stiffened panels by space harmonic expansion method[J].Journal of Sound and Vibration,2002,251(2): 349-366.

[5]XIN F.X and LU T.J.Transmission loss of orthogonally rib-stiffened double-panel structures w ith cavity absorption[J].Journal of the Acoustical Society of America,2011,129(4):1919-1934.

[6]J.Brunskog.The influence of finite cavities on the sound insulation of double plate structures[J].Journal of the Acoustical Society of America, 2005,117(6):3727-3739.

[7]Dassault Systèmes.Aaqus 6.10 Documentation[Z].2010.

[8]T.Buzzi,C.Courné,A.Moulinier and A.Tisseyre.Prediction of the sound reduction index:Amodal approach [J].Applied Acoustics,2003,64:793-814.

[9].王英敏，胡 碰，朱蓓丽.单层薄板在共振频率区隔声性能的有限元分析[J].噪声与振动控制，2006(4)：55-57.

[10].霍 新，杨新文，张小安，李 奇.矩形薄板全频段隔声特性分析[J].噪声与振动控制，2013(3)：34-38.

Finite ElementAnalysis of Sound Transm ission through Unidirectionally Reinforced Sandw ich Plates

WANG Yi-bo1,WEI Zhi-ping1,ZHENG Hui1,2

(1.Institute ofAutomotive Engineering,Shanghai Jiaotong University,Shanghai 200240,China; 2.Institute of Vibration,Shock&Noise,Shanghai Jiaotong University,Shanghai 200240,China)

The sound transm ission loss(STL)of unidirectionally reinforced sandw ich plates w ith typical corrugated cores is analyzed by means of finite element method.Two different FE models,of which one is w ith acoustically-transparent core elements and the other considers the structural-acoustic coupling between the core elements and the fluid inside the enclosed cavities,are respectively created by ABAQUS.The STL curves for the plates w ith different core structures and acoustic media in the cavities are calculated.The results indicate that the error of STL computation of the reinforced sandw ich plate induced by the“acoustically transparent”assumption for the reinforced panels depends on the ratio of the structural resistance of the core elements to the acoustic resistance of the fluid inside the enclosed cavities.Therefore,more accurate prediction of the vibro-acoustic responses and STL of the plates can be achieved by considering the structuralacoustic couplings between the core elements and the fluid in the cavities in the modeling.

vibration and wave;sandw ich plates;sound transmission loss;structural-acoustic coupling;finite element analysis

1006-1355(2014)04-0096-05

TB53；TU112.59+3；O241.82 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.021

内部噪声水平是衡量包括高速机车和飞机等高速载运工具乘坐舒适性的一个主要性能指标参数。加筋双层板广泛应用于飞机机身和高速机车车体，对外部声源，特别是高速行驶时的空气动力噪声起隔声作用。

2013-10-21

国家自然科学基金（基金编号：NSFC 51275285）

王义柏（1987-），男，硕士研究生，目前从事噪声、振动控制领域的研究。

E-mail:huizheng@sjtu.edu.cn