基于云遗传的RBF神经网络的交通流量预测

张 琛，徐国丽

ZHANG Chen1,XU Guoli2

1.甘肃政法学院 实验管理中心，兰州 730070

2.兰州交通大学 数理与软件工程学院，兰州 730070

1.The Experiment Management Center of Gansu Institute of Political Science and Law,Lanzhou 730070,China

2.School of Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

交通诱导和控制是智能交通系统的重要组成部分。实时准确的交通流预测是实现智能交通诱导和控制的前提和关键[1-2]。城市交通流系统具有明显的混沌特征，其短时交通流数据即为混沌时间序列。在此基础上进行预测的思想是构造一个非线性映射来近似地还原原来的系统，而非线性映射就是要建立的预测模型。迄今为止，许多学者在这一领域做了很多的研究，建立了多种交通流预测模型，如Volterra滤波器自适应模型[3]、BP神经网络模型[4]、RBF神经网络模型[5]。在这些预测方法中，神经网络方法因其具有强大的学习能力与良好的泛化推广能力，成为了大量学者研究的热点。但在实际应用中，神经网络中隐层节点中心矢量和宽度值的选取对网络的学习和泛化推广能力有着较大的影响，不恰当的参数选择会严重影响网络的性能[6]。遗传算法（Genetic Algorithm，GA）是借鉴自然界遗传中的自然选择、适者生存的群体优化算法[7]，它训练神经网络无需先验知识、对初始参数不敏感，非常适用于神经网络参数优化。

为了改进传统GA收敛速度慢的缺点，本文提出了一种基于云遗传的RBF神经网络的预测模型（CGARBF），该方法根据正态云模型云滴的随机性和稳定性的特点，采用云发生器代替传统的交叉、变异操作，来弥补RBF神经网络连接权值和阈值选择上的随机性缺陷，从而能发挥RBF神经网络泛化的映射能力，而且能使RBF神经网络具有较快的收敛性以及较强的学习能力。利用该方法对Logistic混沌时间序列和交通流时间序列进行建模和预测分析，结果表明该方法对于典型混沌时间序列和交通流预测具有更好的非线性拟合能力和更高的预测准确性。

1 云理论

1.1 云模型

云模型是李德毅院士提出的一种用自然语言值表示的定性概念与其定量表示之间的不确定性转换模型，主要反映客观世界事物或人类知识中概念的模糊性和随机性，并把二者集成在一起，为定性与定量相结合的信息处理提供了有力手段[8]。

正态云模型是一个遵循正态分布规律并具有稳定倾向的随机数集，隐含了三次正态分布规律，记作：N3(Ex，En2，Hn2)。云的三个数字特征用期望值Ex、熵En和超熵Hn来表示。

1.2 云发生器

生成云滴的算法或硬件称为云发生器。云发生器有四种：正向云发生器，逆向云发生器，X条件云发生器和Y条件云发生器，以下介绍本文将用到的两个云发生器算法。

2 RBF神经网络

RBF神经网络是由输入层、隐含层、输出层组成的一种三层的前馈神经网络，其结构[9]如下图1所示。RBF神经网络完成映射 f:Rm→Rn，数学表达式如式（1）所示：

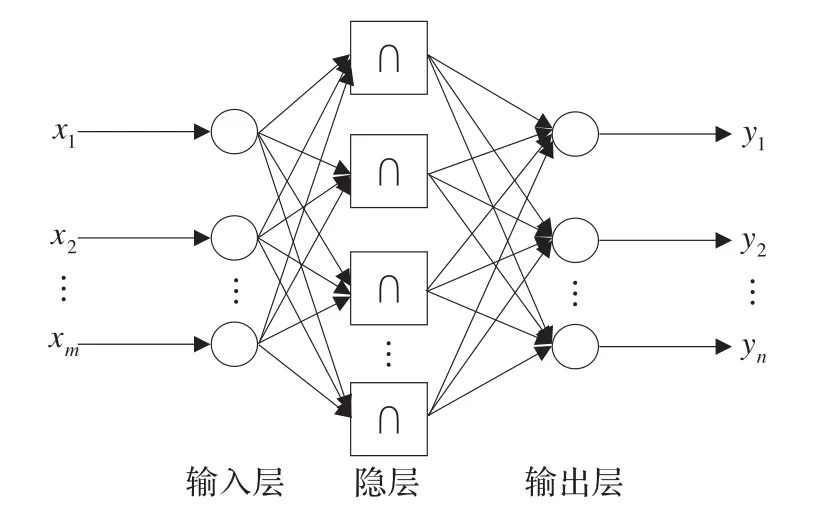
图1 典型的RBF神经网络结构图

取 m=1，x∈Rn为网络的输入向量，ϕ(•)为径向基函数，完成从Rn→R的非线性变换，‖‖•表示范数，θij(1≤i≤m，1≤j≤h)为网络的输出层连接权值，cj为网络的隐含层中心点，θ0为网络的偏置。对于隐含层隐节点个数的确定，可以事先设定一个精度值，隐节点的个数从小到大增加，当网络达到精度时，此时的隐节点个数即是网络的隐节点数。本文选用高斯函数作为径向基函数，其表达式如式（2）所示：

式中β称为宽度。

3 基于云遗传的RBF神经网络的算法设计

3.1 算法基本思想

基于云遗传的RBF神经网络的算法设计结合遗传算法思想，沿用GA的交叉、变异操作，由正态云模型的Y条件云生成算法来实现交叉操作，基本云生成算法实现变异操作对RBF神经网络模型结构中的隐单元中心ci、宽度σi和网络的连接权值wkj这三个参数进行优化，从而产生新一代种群，种群按照以上过程不断优化直至找到最优个体。将云遗传优化得到的最优个体对RBF神经网络的初始权值和阈值进行赋值，再利用RBF神经网络预测模型进行寻优，从而得到具备全局最优解的RBF神经网络预测值，其算法流程图如图2所示。

图2 算法流程图

3.2 基于云遗传的RBF神经网络的算法

算法的基本步骤如下：

步骤1（初始化种群）初始化算法模型参数：群体规模的大小L、隐含层节点的最大数D、变异概率Pm以及最大进化代数G。

步骤2（编码）由于二进制编码具有较大的Hamming距离，会降低遗传算子的搜索能力，因此为了加强该算法在解空间的搜索能力，参数基因均使用实数编码方式，估个体编码的长度与其变量的个数相等。本文对RBF神经网络的参数ci、σi、wki进行统一编码到一个个体中，每一个个体就能代表一个RBF网络结构。

步骤3（适应度函数）在该算法中，适应度函数是描述种群个体中的优劣程度的主要指标。本文选用均方误差作为适应度函数，表达式如式（3）所示：

式中，F为个体的适应度函数值，N为训练样本的总数；tp是第 p个样本的期望输出；yp是第 p个样本的实际输出。

步骤4（选择）

（1）复制最佳个体至下一代；

（2）选择精英群并复制；

（3）最差个体淘汰，被随机产生的个体取代。

步骤5（交叉）

（1）随机生成隶属度 μ0；

（2）Ex由父母双方按适应度的大小加权确定；

（3）En=变量搜索范围/c1（c1为控制参数）；

（4）Hn=En/c2（c2为控制参数）；

（5）由算法2产生两个儿女。

步骤6（变异）

（1）Ex取原个体；

（2）En=变量搜索范围/c3（c3为控制参数）；

（3）Hn＝En/c4（c4为控制参数）；

（4）如隶属度小于变异概率Pm，由算法1得到变异后的个体。

步骤7判断变异后的个体是否有改进，有改进转步骤4，否则将云遗传算法得到的个体分解为RBF神经网络的连接权值和阈值，将此作为预测模型的初始权值和阈值，训练RBF神经网络预测网络，得出混沌时间序列预测的最优解。

4 仿真实验

将提出的CGARBF预测模型应用于Logistic系统和实测交通流时间序列的预测，并与RBF神经网络预测模型和GARBF预测模型进行对比，以此验证该算法的有效性。

4.1 预测评价标准

实验的误差评价主要用到均方根误差RMSE，正则化均方根误差NRMSE和相对均方误差RE，分别如式（4）~式（6）所示：

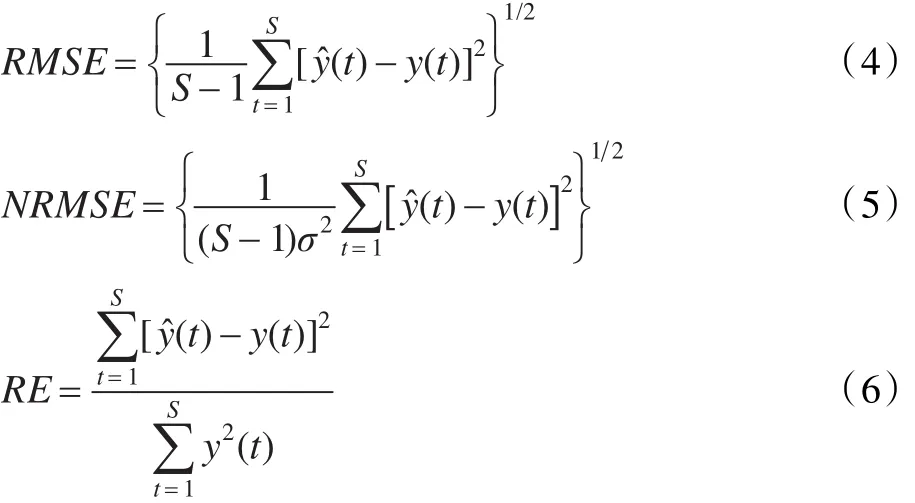
其中S为预测样本数，y′(t)和 y(t)分别为预测值和期望值，σ表示目标时间序列的标准方差。运用下式对实验中的时间序列数据进行归一化，并对归一化后的时间序列按照式（7）进行相空间重构。

其中{xi}为原时间序列，{x′i}为归一化后的时间序列。

4.2 Logistic混沌时间序列预测

由于Logistic方程是比较成熟的、典型的混沌方程，所以许多实际的混沌问题被归结为此方程，因此在选择该方程进行模拟运算结果分析时很具有代表性，该数学表达式如式（8）所示：

当3.57＜μ≤4时，系统状态呈混沌行为。

实验中，Logistic系统的积分时间步长取0.1，嵌入维数m取2，延迟时间τ取5。训练次数取10 000，训练目标误差取0.01，学习率取0.1。云遗传参数设置：种群规模设置为10，进化代数设置为100次，变异概率设置为0.2。取混沌时间序列的前1 500个数据为训练样本，后面500个数据为预测的检验样本。图3给出了Logistic系统的单步预测效果图，表1给出了Logistic系统的预测误差。

图3 Logistic混沌时间序列预测结果图

表1 Logistic系统预测误差

4.3 实测交通流时间序列预测

在单位时间内，通过道路某一观测点或者断面的车辆数，称为交通流量亦称为交通流或交通量，其统计方法如式（9）：

式中V表示某一时刻t的交通流量，T表示统计时间间隔，N代表T时段内的车流数量。

4.3.1 实例1

实例1的交通流量数据来自于英国交通局网上公布的2011年3月的交通数据。观测时间为每天6：00-20：00，每隔15 min记录一次并计算该时刻点的交通流量值。本文取其中5天的数据（336组）作为研究对象。采用文献[10]中计算最大Lyapunov指数的改进算法，计算得该交通流时间序列的最优延迟时间τ为1，最优嵌入维数m为3，最大Lyapunov指数为0.375 4，说明该交通流时间序列为混沌时间序列。

实验取网络训练次数为5 000，训练目标误差为0.01，学习率为0.1，其他参数不变。取交通流序列前236组数据为训练样本，后100组为测试样本，分别用RBF模型、GARBF模型和CGARBF模型对其进行预测，图4给出了在τ=1，m=3的预测结果，表2给出了两种预测模型在不同延迟时间、嵌入维数下的预测误差，以NRMSE为评价指标。

图4 实例1交通流混沌序列预测结果

表2 基于不同延迟时间和嵌入维数的交通流量预测误差

4.3.2 实例2

实例2的交通流数据来自北京某公路监测站的实测数据，观测总时间为4天共96小时。以15分钟为时间间隔，记录每个时段的车辆数，并按式（9）分别计算出各个时间点的交通流量值，总共384组数据。采用文献[10]中计算最大Lyapunov指数的改进算法，计算得该交通流时间序列的最优延迟时间τ为1，最优嵌入维数m为4，最大Lyapunov指数为0.039 2，说明该交通流时间序列亦为混沌时间序列。

取交通流序列前288组为训练样本，后92组数据为测试样本。分别用RBF模型、GARBF模型和CGARBF模型对其进行预测，图5给出了在τ=1，m=4的预测结果，表3给出了两种预测模型在不同延迟时间、嵌入维数下的预测误差，以NRMSE为评价指标。

图5 实例2交通流混沌序列预测结果

表3 基于不同延迟时间和嵌入维数的交通流量预测误差

从图4、图5和表2、表3可以看出两种预测模型的预测结果均能就很好地预测交通流量变化的趋势，CGARBF神经网络预测模型的预测精度高于RBF神经网络预测模型和GARBF神经网络预测模型，从而说明CGARBF预测模型对于实测交通流时间序列的预测是有效地。从表2、表3还可以看出当τ和m取最优延迟时间和嵌入维数时，预测效果最佳。

5 结束语

针对交通诱导与控制对实时性的高要求，以及交通流所显示的非线性、不确定性，本文从非线性时间序列角度出发，采用混沌动力学理论对短时的交通流进行了分析，提出了一种基于云遗传的RBF神经网络优化算法。该算法利用云模型云滴的随机性和稳定倾向性的特点，由正态云模型的Y条件云发生器实现交叉操作，由基本云发生器实现变异操作，提高了遗传搜索的效率，精简了网络结构。将该算法应用于Logistic混沌系统和实测交通流系统的预测，并与RBF神经网络预测模型和GARBF神经网络预测模型进行了预测精度的比较，结果表明，该模型在典型的混沌时间序列和交通流方面具有更好的非线性拟合能力和更高的预测精度，为混沌时间序列预测和交通流预测提供了一种新思路。

[1]Hu J M.An applicable short-term traffic flow forecasting method based on chaotic theory[C]//Proc of IEEE 6th International Conference on Intelligent Transportation Systems，2003，1：608-613.

[2]Smith B.Comparison of parametric and nonparametric models for traffic flow forecasting[J].Transportation Research Part C，2002，10（4）：303-321.

[3]李松，刘力军，郭海玲.短时交通流混沌预测方法的比较[J].系统工程，2009，27（9）：60-64.

[4]董超俊，刘智勇.多层混沌神经网络及其在交通量预测中的应用[J].系统仿真学报，2007，19（10）：101-104.

[5]张玉梅，曲仕茹，温凯歌.基于混沌和RBF神经网络的短时交通流量预测[J].系统工程，2007，25（11）：30-34.

[6]朱万富，赵仕俊.基于粗糙集的神经网络结构优化设计[J].计算机工程与设计，2007，28（17）：4210-4212.

[7]Holland J H.Adaptation in natural and artificial system[M].Cambridge：MIT Press，1975：100-120.

[8]李德毅，孟海军，史雪梅.隶属云和隶属云发生器[J].计算机研究与发展，1995，32（6）：15-20.

[9]樊国创，戴亚平，闫宁.基于RBF神经网络的高斯混合近似算法[J].系统工程与电子技术，2009，31（10）：2489-2526．

[10]李松，贺国光.基于最大Lyapunov指数改进算法的交通流混沌判别[J].武汉理工大学学报，2006（5）：747-750.