基于双振子差分系统的复频检测新方法

胡燕燕，曾芳玲，张诗桂

HU Yanyan,ZENG Fangling,ZHANG Shigui

电子工程学院 安徽省电子制约技术重点实验室，合肥 230037 Electronic and Engineering Institute,Hefei 230037,China

1 引言

随着混沌理论在微弱信号检测领域的应用越来越广泛，人们对弱正弦信号各项参数如幅值、频率、相位的检测研究越趋成熟。众所周知，对幅值进行检测之前必须先已知待测信号的频率，因此对待测信号频率的检测至关重要。目前利于混沌检测弱信号的方法中，对于频率的研究多还是针对单频信号的检测，常用方法是利用间歇混沌原理来实现检测的目的，但此方法振子数目太多，计算量大，检测带宽有限；另外，对复频信号的检测方法也不多见，所以，本文提出结合间歇混沌原理与双Duffing振子系统利用差分方法检测复频信号的新方法，使检测效率得到了有效的提高。

2 双Duffing振子差分方程检测原理

在检测范围内，特定参考频率的Duffing振子不受其他频率信号的外界干扰，只对其附近的一小部分特定频率信号敏感[1]。

利用这一特性，得出有可能同时出现小幅值周期运动和间歇混沌运动的结论，这说明待测信号中除了可以检测出单频信号以外，有同时存在两个不同频率的正弦信号的可能，即复频信号，否则，无弱正弦信号存在。

2.1 双振子差分模型

在单Duffing振子测频的基础上对其进行改进，建立模型：

式（1）中两振子相对独立且不完全耦合，除了α不同之外，其余数值完全相同，且α≠1。由于差分作用，振子1的时域x1与振子2的时域x2有相位的差别，输出时取其差值x1-x2，此处设α值为1.001。

调整γ1=0.826，使振子1处于临界状态的，α值驱动振子2进入大尺度周期状态；加入待测周期信号后，振子1变为大尺度周期状态，振子2仍为周期态，利用差分能抑制共模信号、放大差分信号的作用，此时系统差分输出为一幅度很小的规则周期信号，从而判断出微弱正弦信号的存在[2]。

2.2 差分测频具体步骤

双振子系统检测频率与传统Duffing振子阵列法基本原理基本相同，但公比取值范围在1.06~1.08之间[3]，具体步骤如下：

步骤1设置系统各参数，使振子1参数在混沌阈值处，使振子2处在大尺度周期状态。

步骤2选取∆ω为0.06~0.08[3]，则检测频率的范围可达(0.94~1.08)ω0，建立双Duffing振子阵列频率检测模型，以1.06n，n∈[1，40]或者1.08n，n∈[1，30]的数值设置各振子组的振子频率。

步骤3将待测信号加入到系统，生成差分输出时序图(x2-x1)-t。

步骤4判定。（1）若某双振子组系统输出为一幅度很小的规则周期信号，则待测信号频率就等于该振子的驱动力频率；（2）若某两相邻双振子组输出为周期不同的间歇混沌，则待测信号频率就等于这两个振子的驱动力频率的算术平均值；（3）若两种现象都存在，则存在复频信号。

具体流程图如图1所示。

在下面的仿真中，对单频信号检测∆ω=0.06；对复频信号，为了减少误判，频差提高到∆ω=0.08。这里∆ω比传统方法0.01取值大很多，避免参考频率因相差不大导致都在待测信号频率附近而同时发生相变，并因此产生的误判，在某种程度上说，提高了检测精度[4]。

图2 未加入周期信号前的差分系统相态图

图1 双振子差分法弱信号频率检测流程图

3 仿真实验

3.1 双振子差分法检测弱信号

据差分原理，图2是振子频率ω=1 rad/s的差分系统在未加入周期信号前的相态图如图2。

系统分别加入弱正弦信号0.02 cos(t)和加入信噪比为 -19 dB的高斯白噪声（之后的仿真中皆用此噪声）0.02 cos(t)+n(t)后的相态图，如图3（a）和3（b）。

图2和图3对比，系统发生了相变，由混沌临界状态变为大尺度周期状态，证明有弱周期信号存在[5]。

加入噪声后，差分系统输出时序图如图4。

从(x2-x1)-t上看，发生相变后的差分输出为一幅值为±0.3的小幅值规则周期图像，说明该系统对加入的周期信号敏感，发生了相变，弱正弦信号是存在的，且加入噪声不影响判断[6]。

3.2 双振子差分法对单频信号的检测

双Duffing振子各自构建以公比为1.06的振子阵列，第n个振子的驱动力频率为100×1.06n-1rad/s，振子数为40[7]，初始频率ω0为1 rad/s，在高斯白噪声背景下，将待测信号a cos(1.105t)，a=0.5的正弦信号加入系统，待测信号频率为110.5 rad/s，预计会在第二和第三个振子间出现间歇混沌，仿真结果如图5。

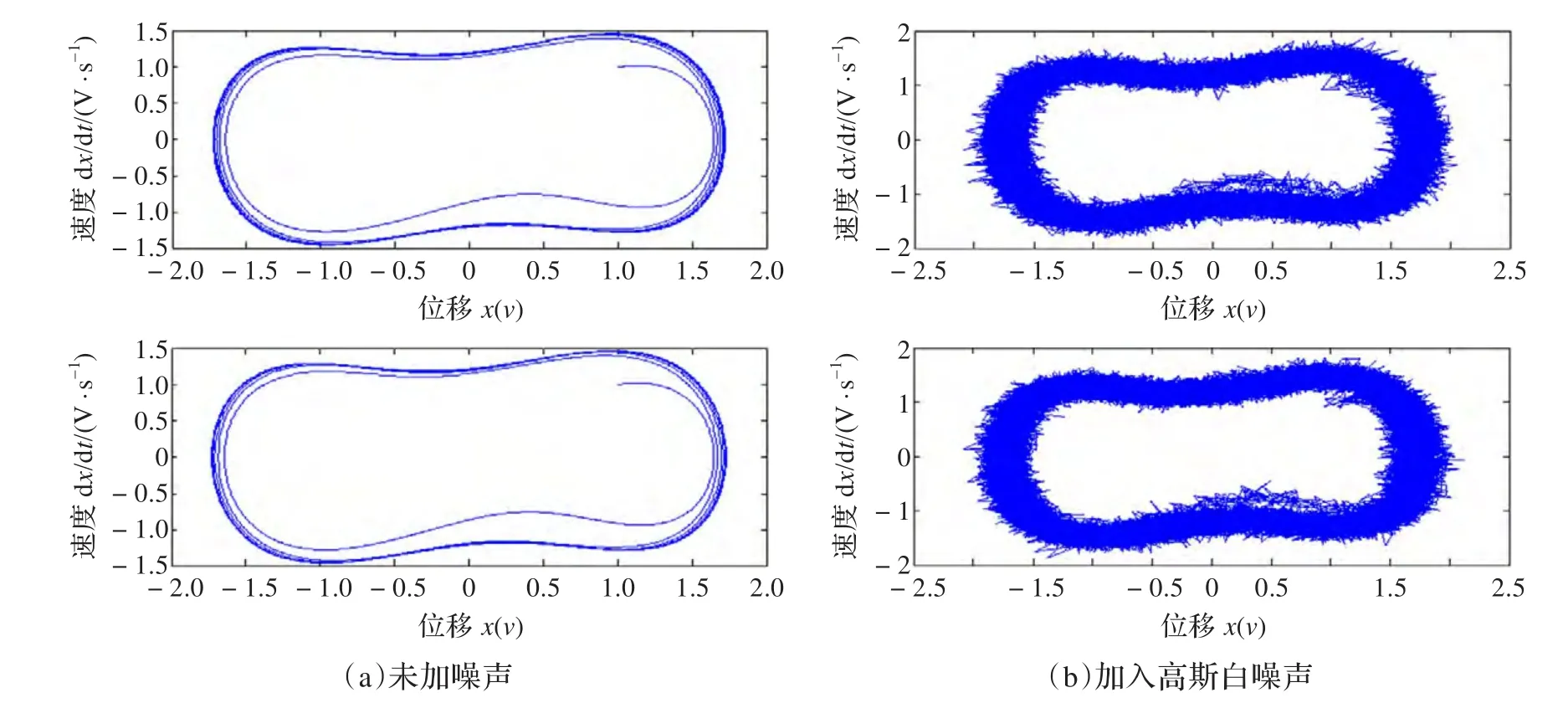
图3 加入周期信号和噪声后的差分系统相态图

图4 加入0.02cos(t)+n(t)的差分振子时序图

图5 公比为1.06的差分振子阵列加入待测信号的差分序列输出(ω 分别取值 ω0＝1.00 rad/s，ω1＝1.06 rad/s，ω2＝1.123 6 rad/s)

图5 所示，ω0的差分序列没有任何周期性，表现为混沌态；ω1和ω2的为稳定的间歇混沌，所以待测信号频率为[8]：

与真实值相比，误差为1.32 rad/s，其相对误差为：

3.3 双振子差分法对复频信号的检测

确立策动力幅值阈值为0.826，构造同上的双Duffing振子阵列，将初始频率ω0改为0.92 rad/s，公比改为1.08，检测频率范围为(0.92~1.08)ω0，第n个振子的频率为0.92×1.08n-1rad/s，振子数为31个。设在高斯白噪声背景下，将复合信号 a1cos(ω1t)+a2cos(ω2t)(ω1=0.96，ω2=1.07)作为待测信号加入到差分系统里，其中，a1=0.02，a2=0.5，仿真结果如图6。

图6 公比为1.08的差分振子阵列加入待测信号后的差分系统输出前三个振子组差分输出(ω分别取值ω0=92 rad/s，ω1=99.36 rad/s，ω2=107.31 rad/s)

ω2的差分时序输出为小幅值的规则周期图像，幅值为±0.4 V；而ω0和ω1的时序差分输出为间歇混沌。

据间歇混沌理论，此待测信号有一个信号频率与ω2的频率相同为1.0731 rad/s，与真实信号频率的误差为

另外ω0和ω1的差分序列也可确定一个待测信号的频因此系统平均的相对误差为0.883 5%。

此方法比传统的方法更直观易辨，若最后的仿真时序图表示为一段直线和一段不规则波形的规律组合，则判断系统表现为间歇混沌，如图5的第二个波形；若一直为恒定的小幅值规则波形，则为周期运动，如图4的第三个波形；否则为混沌运动，如图5的第一个波形，最后结合间歇混沌原理检测弱周期信号。

4 与传统单个振子阵列法的比较

4.1 传统Duffing振子阵列测频

对传统方法进行仿真如下：

设待测信号为s(t)=a cos(ωt)+n(t)，其中，a=0.2，ω=1.15 rad/s，将其加入传统单个Duffing振子检测系统，振子数为232个，检测带宽为(0.99~1.01)ω0，仿真结果中，寻找最大周期对应频率为待测信号频率[9]，如图7。

理论上，第15个振子周期性最强，周期最大，明显为待测频率[10]，而图7中，第15个振子只可以勉强与理论结果相匹配，判定为待测信号频率为114.95 rad/s，虽然此时相对误差很小，但是图7中可以看出，时序图中的周期性并不是很明显，要判定出结果，主观性很强，甚至容易出现误判的情况，所以它的平均相对误差要比新方法的大，相同SNR下，错误概率也相对较大。

图8 新方法与传统方法抗噪性能比较

图7 系统中加入s(t)=a cos(ωt)+n(t)输出的第13~19个振子时序图

4.2 抗噪性能比较

仿真如下：图 8（a）和（b）为差分振子在信噪比为-17 dB的情况下的间歇混沌，随着待测信号幅值的不断减小，尤其是在幅值从0.203降到0.197时，系统的间歇混沌开始变得不明显；同理，图8（c）和（d）为传统方法在信噪比为 -9 dB情况下的间歇混沌，在幅值由0.3降到0.2时，系统的状态开始难以辨认，因此可以得出：新方法的抗噪性能比传统方法更好，更容易辨认，减小了误判率，而且信噪比也降低了8 dB，并且更容易检测更微小的信号。

对于Duffing振子而言，噪声在一定范围内（这个范围需要考虑系统的最低信噪比门限）对系统的影响仅仅是使相轨迹变得粗糙，粗糙的程度由其方差决定，换言之由信噪比决定。当系统原有的运行轨迹发生变化时，则可以判断最低检测门限[11]，如表1，以方差为0.001的高斯白噪声为例。

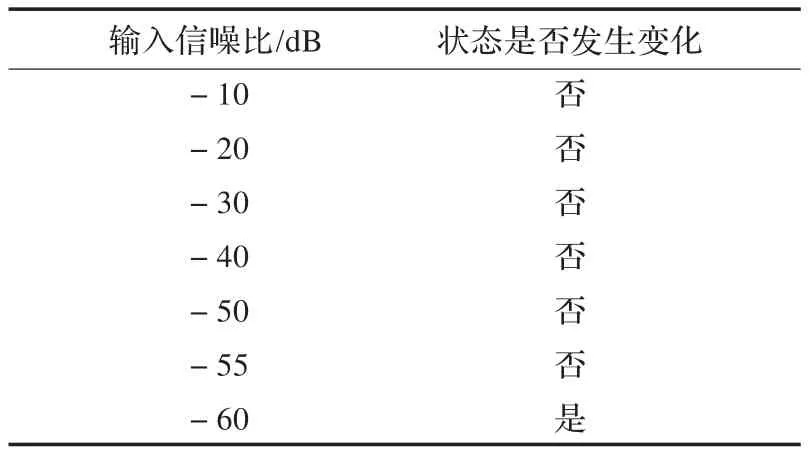
表1 方差为0.001时刻的系统最低检测门限判断

表1显示，在 -60 dB时，系统状态发生改变，-55 dB是状态没有发生变化，所以此刻最低信噪比门限为-55 dB。

其中，信噪比可定义为下式：

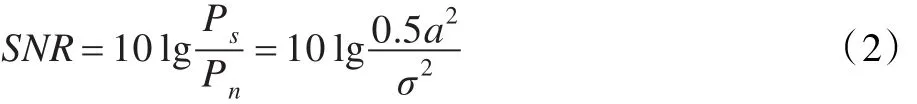
Ps和Pn分别表示信号功率和噪声功率，a表示待测正弦信号的幅值，σ表示加入的高斯白噪声的均方差。

因此，不同方差，系统的最低检测门限是不同的[12]，相同方法得出表2。

表2 不同噪声方差下的系统的最低检测门限

4.3 双振子差分法与传统方法的其余参数比较

新方法与传统的间歇混沌频率检测法比较，公比的选取也存在着很大的差异[13]，从而使振子数由232降低误判率得到了有效的降低，抗噪性能比传统方法优越，工作量也得到了有效的控制，具体的比较见表3。

表3中，改进的双振子阵列差分法，振子数比传统单个振子阵列法的振子数要少得多；检测带宽也比传统方法的检测带宽大的多。

综上所述，传统测频方法虽然也可以实现较宽频率范围的弱周期信号的检测[15]，但主观依赖性强，计算量大，有时，间歇混沌现象并不十分明显，甚至出现误判；而双振子差分法，检测结果更简单，更直观，从波形上就可以直接辨认出信号的运动形态，而且可以更进一步增大检测带宽，抗噪性能也很理想。

表3 传统振子阵列法与双振子阵列比较列表

5 结束语

本文将两个Duffing振子组合成双振子差分系统，并结合传统方法，得出检测弱信号频率的新方法。根据对应的波形特征进行分析，系统输出结果分三种情况：（1）若系统差分输出表示为一段直线和一段不规则波形的规律组合，那么判断为间歇混沌；（2）若一直为恒定的小幅值规则波形，则为周期运动；（3）否则为混沌运动。

最后在仿真中与传统方法[16]进行比较，此方法比传统的更直观易辨，而且结果也显示了其检测带宽比传统方法有所增加，大大减小了计算量，检测效率也有所提高，抗噪性能优越，虽然精度上与传统方法有微小的差异，但是其平均相对误差还是很可观的，是一种很好的频率检测方法。

[1]李瑜，章新华，肖毅，等.杜芬振子阵列实现弱正弦信号频率检测[J].系统仿真学报，2006，18（9）：2650-2656.

[2]任志玲，刘银报，史旭鹏.基于Duffing振子的弱正弦信号检测的改进[J].计算机测量与控制，2011，19（6）：1301-1303.

[3]王玫，颜勇，张慧峰.基于双Duffing振子差分的微弱信号频率检测[J].电路与系统学报，2010，15（2）：119-121.

[4]朱志宇，姜长生，张冰，等.基于混沌理论的微弱信号检测方法[J].传感器技术，2005，24（5）：65-68.

[5]李月，陆鹏，杨宝俊.用一类特定的双耦合Duffing振子系统检测强色噪声背景中的周期信号[J].物理学报，2006，55（4）：1672-1677.

[6]姜万录，王益群，孔祥东.齿轮故障的混沌诊断识别方法[J].机械工程学报，1999，35（6）：44-47.

[7]李月，杨宝俊，石要武，等.纳伏级正弦信号的混沌检测方法研究[J].通信学报，2003，24（3）：25-30.

[8]吕金虎，陆安君.混沌时间序列分析及应用[M].武汉：武汉大学出版社，2005.

[9]Wang Guanyu，Chen Dajun，Lin Jianya，et al.The application of chaotic oscillators to weak signal detection[J].IEEE Transactions on Industrial Electrons，1999，46（2）：440-444.

[10]叶亦能，王林泽.基于Duffing振子的噪声背景下微弱周期信号检测[J].机电工程，2009，26（4）：97-100.

[11]聂春燕.基于混沌相平面变化的弱信号检测方法研究[J].长春大学学报，1999，9（4）：1-4.

[12]李月，杨宝俊，石要武.色噪声背景下微弱正弦信号的混沌检测[J].物理学报，2003，52（3）：526-530.

[13]李瑜，章新华，肖毅，等.杜芬振子阵列实现弱正弦信号频率检测[J].系统仿真学报，2006，18（9）：2650-2656.

[14]王永生，姜文志，赵建军，等.一种Duffing弱信号检测新方法及仿真研究[J].物理学报，2008，57（4）：2053-2058.

[15]衣文索，石要武，聂春燕.混沌态杜芬振子与弱正弦信号参量估计[J].计量学报，2006，27（2）：156-159.

[16]周畅，张建科.一类非线性极小极大问题的粒子群-邻近点算法[J].计算机工程与应用，2012，48（36）：19-22.