基于努赛尔方程的逆流管式换热器的性能研究

(天津现代职业技术学院，天津 300350)

换热器是化工、石油、能源等工业中应用相当广泛的单元设备之一。新型换热元件与高效换热器开发研究的结果表明, 列管式换热器已进入一个新的研究时期, 无论是换热器的传热管件, 还是壳程的折流结构，都比传统的管壳式换热器有了较大的改变[1]。本文以努赛尔方程为基础建立数学模型，通过计算逆流管式换热器的多个设计参数，并验证所选用的数学模型是否合适，为数学模拟该型换热器提供可行的方案。

1 换热系数

1.1 总换热系数

为了计算换热管管内表面积，需要计算相对应的总换热系数Ui；为了计算换热管管外表面积，需先计算相对应的总外换热系数Ue。Ui、Ue的计算方程分别如下：

(1)

(2)

式中：Di——换热管的内径；

De——换热管的外径；

hi——换热管内的局部换热系数；

he——换热管外的局部换热系数；

k′——不锈钢的热导率；

e——换热修正系数。

1.2 局部换热系数

为了计算管内和管外的局部换热系数hi和he，需要使用努塞尔方程[2～5]：

(3)

式中：Nu——努赛尔系数；

h——流体的对流导热系数；

k——静止流体的导热系数。

如果可以确定努赛尔系数，就可以求得hi和he。但是需要特别注意的是，对于hi和he来讲，它们所对应的努赛尔系数是不同的。因此，需要使用到如下不同的方程。

(1)换热管内部

Nu=0.023Re0.8Pr0.4

(4)

(5)

(6)

(7)

(2)换热管外部

(8)

(9)

(10)

(11)

(12)

(13)

Gm=(GlGt)1/2

(14)

式(4)中，Re为雷诺数，Pr为普兰德数。式(5)中，G为空气的质量流量，μ为空气在参考温度下的粘度，下角标“m“表示平均值。式(6)中，w为空气的体积流量，Dc为换热器折流板的直径；n为换热管的数量。式(7)中，Cp为空气的定压比热。式(9)中，Gm为质量流量。式(10)中，a为对流传热系数，下角标“1”表示换热器非折流板部分。式(11)中，ε为换热器非折流板部分(即空白部分)的横截面积与换热器折流板总的横截面积之比。式(12)中，下角标“t”表示换热器折流板部分。式(13)中，B为折流管之间的间距。

2 换热温差

表1为逆流管式换热器换热参数的理论计算结果。这些结果中除了前面推导过的总换热系数

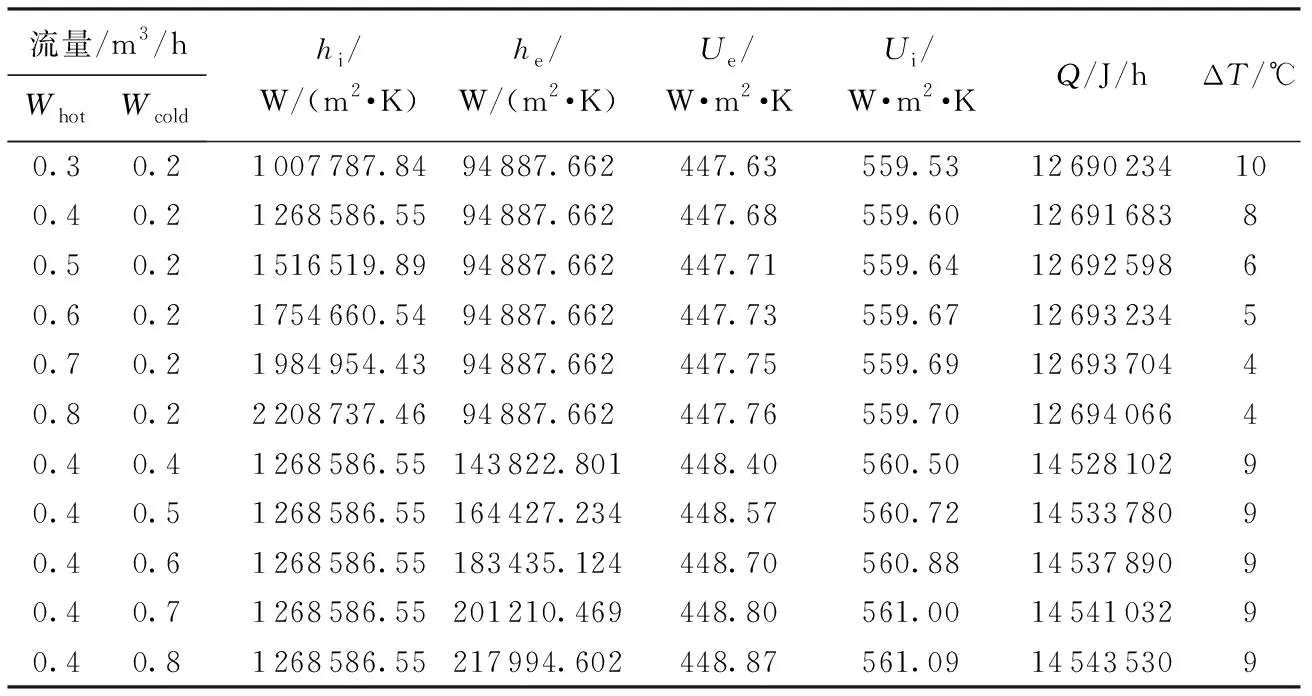
表1 逆流管式换热器各换热参数理论计算结果

表2 逆流管式换热器换热效率实验的计算结果

U、局部换热系数h外，还包括了冷热流体间的换热量，以及热流体在换热器进出口的温差ΔT。这些理论数据的计算使用与后期的实验数据计算相同的公式，以便进行对比研究。

3 实验结果(表2)与讨论

由表2可以看出，增加冷热流体的流量，换热量也随之增加，并导致换热效率的增大。还可以看出，对于换热效率来讲，冷流体的流量变化比热流体的流量变化更为重要。比较换热温差，实验数据要略高于理论计算数据，考虑到实际生产过程中存在的热损耗，该误差在合理的范围内。比较理论计算结果与实验结果, 换热系数基本上是相同的，这也就验证了所选用的数学模型是合适的，为数学模拟逆流管式换热器提供了可行的方案。

参考文献：

[1]冯国红，曹艳芝，郝红.管壳式换热器的研究进展[J].化工技术与开发，2009，38(6)：41～45.

[2]杨明，孟晓风，张卫军.管壳式换热器的一种优化设计[J].北京航空航天大学学报，2009，54(5)：615～618.

[3]王永平.列管式换热器的设计计算[J].内蒙古石油化工，2009，34(7)：95～96.

[4] 林宗虎.管式换热器中的单相流体强化传热技术[J].自然杂志，2013，36(5)：313～319.

[5] 马进，王兵树，马良玉.管式换热器动态数学模型的跷跷板效应分析[J]. 系统仿真学报， 2006， 18(5)：1105～1107.