基于相位校正的零点约束直达波抑制方法
2014-08-30黄聪张殿伦孙大军兰华林
黄聪,张殿伦,孙大军,兰华林
(哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001)
相对于传统收发合置的单基地声呐,双、多基地声呐可以通过多样的配置方式来实现更高的性价比,且由于其收发分置的工作方式,双、多基地声呐具有很好的隐蔽特性。可以说双、多基地[1-2]声呐在一定程度上综合了主动声呐和被动声呐的优点。但同时也带来了不少新的问题[3-4],其中强直达波的干扰抑制是多基地声呐中亟须解决的关键技术之一。在收发分置的系统中,发射站的位置相对于接收站是已知的,则直达波相对于目标回波可以当做固定方位的强相干干扰信号。现存的直达波抑制方法主要可以分为信号的时域对消和空域滤波两大类。干扰抑制技术就是通过对干扰方向信号的抑制,来提取出系统的期望信号[5]。文献[6]利用自适应分数延迟技术进行直达波的对消,不足之处是需要精确的直达波信号模型来提供参考;文献[7]提出了基于矢量阵的强相干干扰抑制技术,但无法应用于常规的声压阵;文献[8]采用线性约束最小方差算法在预设方向进行零陷,但是需要计算信号协方差的逆矩阵,计算量庞大;文献[9]提出了基于均匀圆阵零点技术的相干干扰抑制方法,但权值计算的收敛性和稳定性难以兼顾;文献[10]提出一种基于零陷展宽技术的多约束最小方差直达波抑制算法,通过施加线性约束对特定方向的干扰进行抑制,但MCMV算法需要借助阵列接收矩阵的协方差求逆来计算权值,对于阵元数较多的大型阵列运算量巨大,文献中零陷展宽的方法是在直达波角度附近加入多个虚拟干扰源,这也增加了协方差的计算量。且并未分析相位误差对算法性能的影响。
针对现存的问题,给出了基于波束零点约束的直达波抑制方法,该方法是一种空域滤波方法,其计算量小、易于实现,且可适用于任意阵形。文中对算法的性能进行了仿真分析,并针对该算法对相位严苛的要求,提出了基于直达波相位校准的改进方法。
1 多基地声呐中的直达波干扰
以典型的一发一收的双基地配置为例[11],如图1所示。其中T为发射站,R为接收站,S为目标;τT为声波由发射站传播到目标的时间,τR为目标回波由目标传播到接收阵的时间,τDB为直达波由发射站传播到接收阵的时间。双基地声呐由于收发分置,其探测范围与单基地声呐有所不同。在各向同性的噪声环境下,双基地的最大可探测范围是以收、发基站为焦点的卵形线,如图1中的虚线所示。
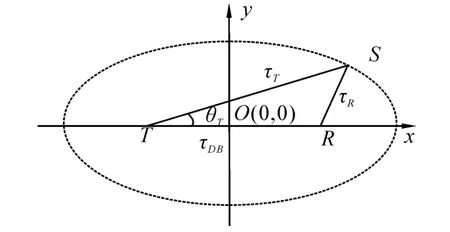
图1 双基地配置示意图Fig.1 Sketch map of bistatic sonar
由于直达波为强相干干扰,在与直达波几乎同时到达的目标回波信号会被掩蔽在直达波信号中而无法被正确检测。即满足:
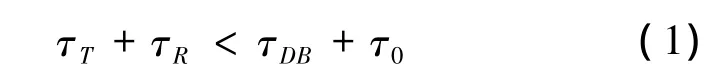
式中:τ0为直达波的脉宽和拓展。故双基地声呐在近距离上将出现盲区,此时就需要对直达波进行抑制才能不影响目标的方位估计,且直达波与目标回波是强相干的,这对目标信号的提取和定位都带来了很大的困难。双基地系统受直达波干扰的掩蔽区域[12]的面积S为
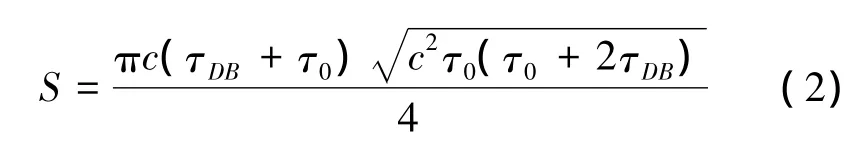
可以看出基线越长,工作脉宽越大,相对应的掩蔽区域面积越大。
2 零点约束下的波束图合成
利用收发分置系统中基站配置的先验知识,直达波的方向通常可以通过先验信息获得。故可以通过在阵列方向图的直达波方向上加上零点约束[13]条件来进行直达波干扰抑制。由于零点约束波束形成对阵列模型没有要求,故可适用于任意阵形中。若目标回波的角度为θi,相干干扰信号角度为wH。要求在阵列输出的θj方向上产生零陷来进行相干干扰抑制,则设计最优权向量wH,在零点约束条件下的阵列波束形成输出为
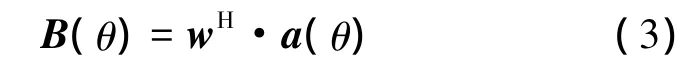
式中:a(θ)为阵列流行向量,B(θ)为零点约束条件下的阵列波束输出。假设Bd(θ)为理想的常规波束图,计算两者之间的最小二乘,可得
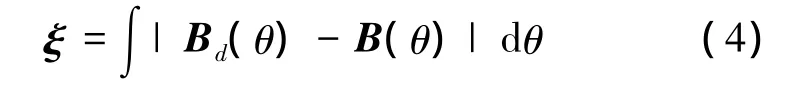
将式(3)代入式(4),可得代价函数为
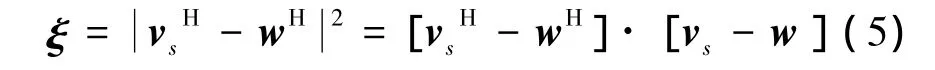
式中:vs
H为常规波束形成的权值。引入拉格朗日乘子λ,可得到代价函数G为
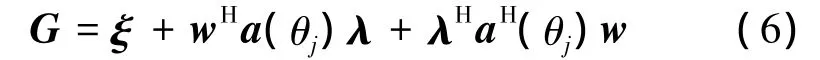
代价函数G对w进行求导,得到最优权向量wH为
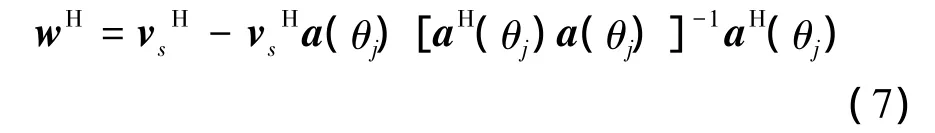
令 P=a(θj)·[aH(θj)a(θj)]-1·aH(θj),则
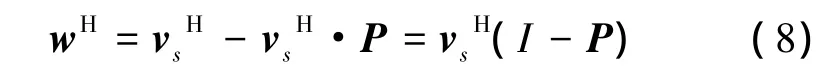
若需要对多个相干干扰进行抑制,则可以通过加入多个零点约束条件来实现。若相干干扰的方位分别为 θj1,θj2,…,θjm,则可将零点约束矩阵扩展为C0,满足 wH·C0=0,C0=[a(θj1)a(θj2)… a(θjm)],式(7)中的wH可改写为
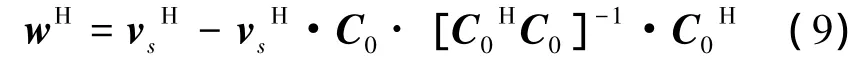
式(9)中的约束条件被称为零阶零点约束条件,若在零阶零点约束条件的基础上,同时使C0的导数也满足零点约束条件,这样就构成了高阶零点。将最优权值代入式(3)中,得到的波束图为
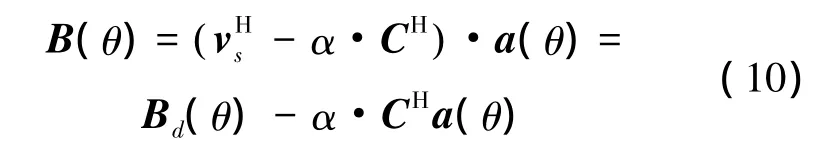
式中:α=vHs·C·[CHC]-1。由式(10)可以看出零点约束的最优权值wH是理想权值vHs减去约束矩阵的加权α·CH。加入零点约束条件的波束输出响应相当于理想的波束输出响应Bd(θ)减去零点位置处的常规波束及其导数的加权响应α·CHa(θ)。
由于直达波的方位可能存在误差,一般可以在直达波的干扰方向附近设置多个低阶零点,增大零点约束波束输出在干扰方向的零陷宽度。下面分别在39°~41°上设置3个零阶零点,38°~44°上内设置6个零阶零点,零点约束的波束输出响应如图2所示。

图2 基于零点约束的波束图Fig.2 Beam pattern based on zero constraint conditions
由图2可以看出,基于零点约束的波束图可以在放置零点的位置产生零陷,若要求产生的零陷对直达波的抑制能力大于40 dB,放置3个和6个零阶零点的波束图对直达波角度扰动的容限分别为38°~44°和30°~55°。但是总约束条件的个数需要小于阵列的阵元数,否则将导致CHC奇异。
下面利用零点约束波束形成对混有直达波的目标回波进行方位估计,仿真在直达波的方位附近放置多个零阶零点,给出利用零点约束波束形成进行方位估计的方位谱。信号频率f=375 kHz,采样频率fs=137 kHz。接收阵为80元的等间隔线阵,阵元间距为半波长。直达波干扰和回波信号在时域上发生混叠,两者的角度分别为-15°和15°,直达波比目标回波的能量高40 dB,目标回波的信噪比为10 dB 。在-14°、-15°、-16°3 个方向设置零阶零点约束条件,分别给出常规波束形成与零点约束的方位谱,二者均用常规波束形成输出的最大值进行归一化。仿真结果如图3所示。
通过常规波束形成方位谱与零点约束方位谱对比可以看出,由于直达波的能量高出目标回波40 dB,常规波束形成的目标回波主瓣被直达波的旁瓣所淹没,只能估计出直达波的方位。而基于零点约束的方位谱能够在直达波方位附近形成零陷,在目标回波的方向上形成波峰,且目标回波峰值的能量与直达波的能量相差40 dB,也与仿真条件吻合。
但由于加入零点约束条件的波束输出响应相当于理想的波束输出响应减去零点位置处的常规波束及其导数的加权响应。当放置零点约束的位置靠近的目标回波的主瓣,形成的零陷将对目标回波的主瓣产生影响,甚至导致无法估计目标的方位。
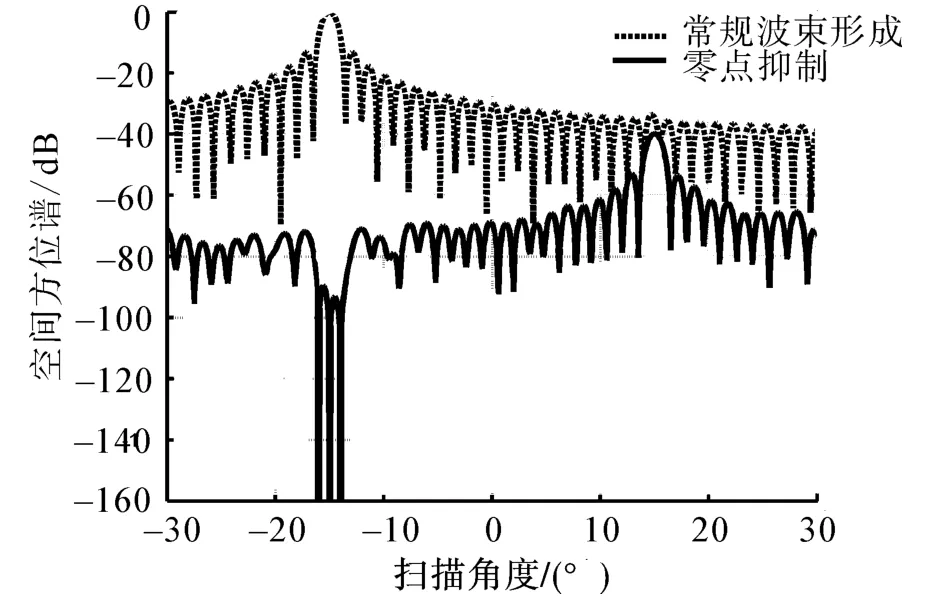
图3 常规波束形成和零点约束的方位谱对比Fig.3 Spectrum of CBF and Beamforming based on zero constraint conditions
3 基于相位校正的直达波抑制
现实的工程应用中,阵元的互耦、阵列幅相不一致、海洋环境等因素的影响,都将导致实际的阵列流型与理论模型出现偏差[14]。阵列模型的偏差对很多的阵列信号处理方法性能产生影响,这需要阵列处理的算法有较好的稳健性。下面分析阵列相位误差对零点约束方位谱性能的影响。
3.1 相位误差对直达波抑制性能的影响
零点约束方位谱能够在直达波干扰的主波束方位附近位置产生零陷,而阵列相位误差导致波束形成时直达波的旁瓣不规则,造成式(10)中的α·CHa(θ)无法完全抵消掉实际数据中直达波的旁瓣,导致零点约束方位谱的性能下降。下面分别给出阵元数为40和80时,不存在相位误差的理想情况和存在σφ=1.2°的相位误差时的零点约束方位谱,直达波干扰和回波信号在时域上发生混叠,入射角度分别为-15°和15°,直达波比目标回波的能量高40 dB,其他仿真条件与图3相同。
图4(a)中阵元数N=40,零点约束方位谱在直达波的主波束附近能够产生零陷,直达波的主波束得到了较好的抑制,但旁瓣却要高出理想情况很多;图4(b)中增加阵元数N=80,零点约束方位谱直达波的主波束得到了较好的抑制,但方位谱的旁瓣同样升高,主旁瓣比由理想情况的13 dB左右下降为8 dB。可以看出相位误差导致零点约束方位谱的旁瓣升高,影响方位估计的性能。而增加阵元数,可以减少相位误差对零点约束方位谱性能的影响。
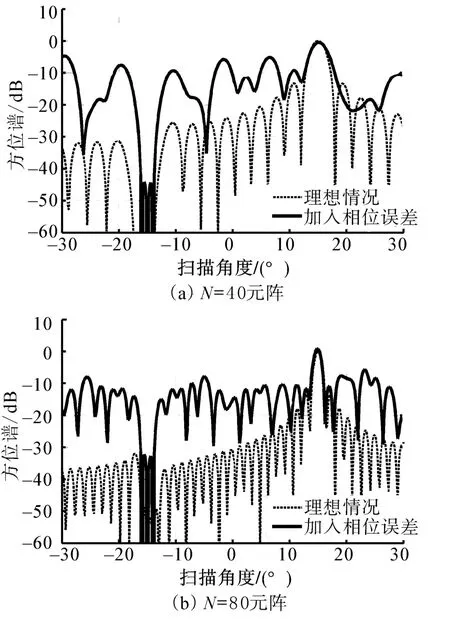
图4 理想情况和存在相位误差的方位谱对比Fig.4 Spectrum without phase error and with phase error
进一步讨论相位误差对零点约束方位谱性能的影响,分别给出检测概率随相位误差的变化曲线,零点约束波束输出的主旁瓣比随相位误差的变化曲线和方位估计的成功概率随相位误差的变化曲线。
为了对目标方位估计是否成功进行判断,给出下面2个条件:1)零点约束方位谱的峰值位置与目标的真实方位偏差小于3°;2)零点约束方位谱的主旁瓣比大于5 dB。
图5为直达波能量高出目标回波40 dB时的检测概率曲线随相位误差标准差的变化曲线,可以看出在虚警概率为5%时,若要求检测概率高于90%时,相位差的标准差需要小于1.8°。从图6可以看出,在直达波能量高出目标回波40 dB时,要求零点约束方位谱的主旁瓣比大于5 dB,相位误差的标准差需要小于1.4°。从图7中可以看出,在直达波能量高出目标回波40 dB时,要求目标方位估计的成功概率大于70%,则需要相位误差的标准差小于1.2°。可见基于零点约束的直达波抑制方法对阵列接收信号的相位要求十分严苛,这是由于当直达波和目标回波在时域上发生混叠时,接收信号中包含有直达波和目标回波的相位信息,常规的波束形成可以同时对直达波和目标回波进行方位进行估计,因为直达波要比目标回波强,目标回波的主瓣淹没在直达波的旁瓣中。当阵列的相位信息存在误差时,零点约束波束形成无法完全消除直达波的旁瓣,导致目标方位估计的性能下降。
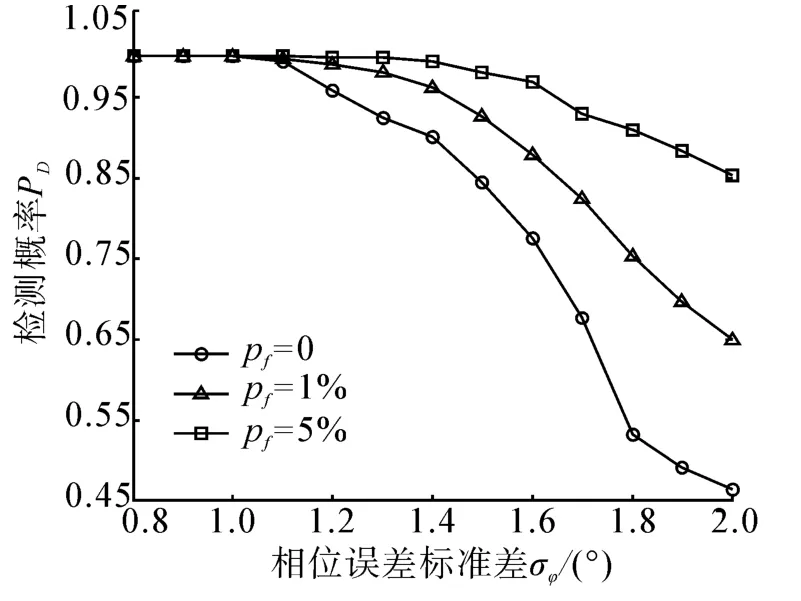
图5 检测概率随σφ的变化曲线Fig.5 Probability of detection with phase error
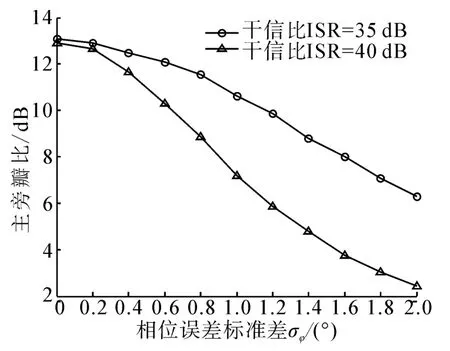
图6 主旁瓣比随σφ的变化曲线Fig.6 Main lobe to sidelobe with phase error
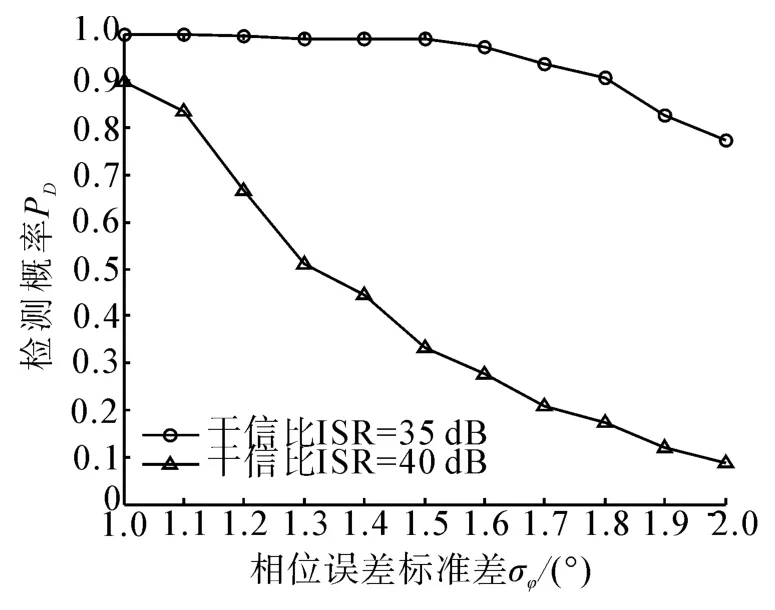
图7 成功概率随σφ的变化曲线Fig.7 Probability of DOA with phase error
3.2 基于相位校正的零点约束直达波抑制方法
由于算法对直达波方向的相位有严苛的要求,本文提出的改进方法是利用直达波在短时间内的方位不改变的特性,先估计出直达波的方位,对阵列的相位进行校正,将信号中所含的直达波相位校正为理论的阵列相位后,再进行零点约束波束形成。在稳定水声信道环境下,由于直达波的信噪比很高,且CW脉冲的持续时间有限,在毫秒量级,故直达波回波在单个脉冲内的阵列相位信息变化不大。而在复杂水声环境中,直达波的前段和后段的相位发生变化时,校正后残留的相位就会导致零点约束波束形成无法完全消除直达波的旁瓣。若直达波在短时间内方位不变,而目标的常规波束形成对相位的宽容性较好,则校正后的阵列相位对目标的方位估计不会造成影响。其流程框图如图8所示。
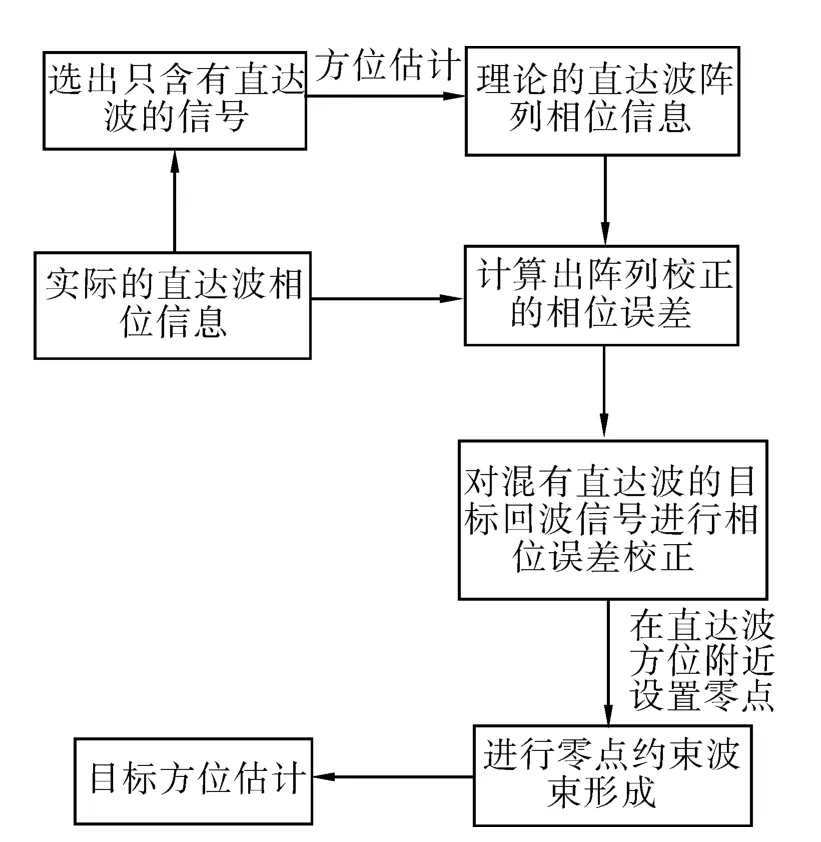
图8 直达波相位校正流程图Fig.8 Flow diagram of direct path wave with phase correction
在宽阔水域,信号多途拓展不明显的情况下,直达波和目标回波的持续时间是相同的。由于直达波的高信噪比性,很容易得到直达波的起始时刻,若还能检测到目标回波的截止时刻,便可以推算出只含有直达波信号的持续时间。
参照图9中的信号模型,假设只含有直达波的信号为direct1,可以得到直达波direct1的阵列相位信息Phase1。直达波和回波信号的重叠部分为recieve=direct2+signal。由于直达波方位的先验信息,利用直达波的方位可以得到直达波的理论阵列相位为Phase_th,利用直达波在短时间内的阵列相位信息不改变的特性,可得到阵列的校正相位为
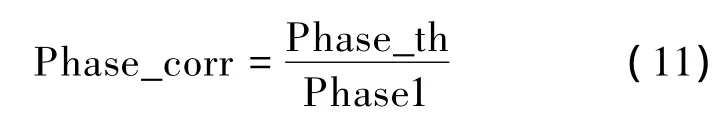
再利用得到的校正相位Phase_corr对接收信号recieve进行相位校正。校正后接收信号中直达波direct2的相位非常接近直达波的理论阵列相位Phase_th,再进行零点约束波束形成后,直达波的旁瓣能够很好地被抑制,从而估计出目标的方位。在图4(b)中存在相位误差的情况下进行直达波相位校正,校正后的零点约束方位谱如图10所示。图10中虚线为校正后的常规波束形成方位谱,校正后直达波的旁瓣与理论值很接近。
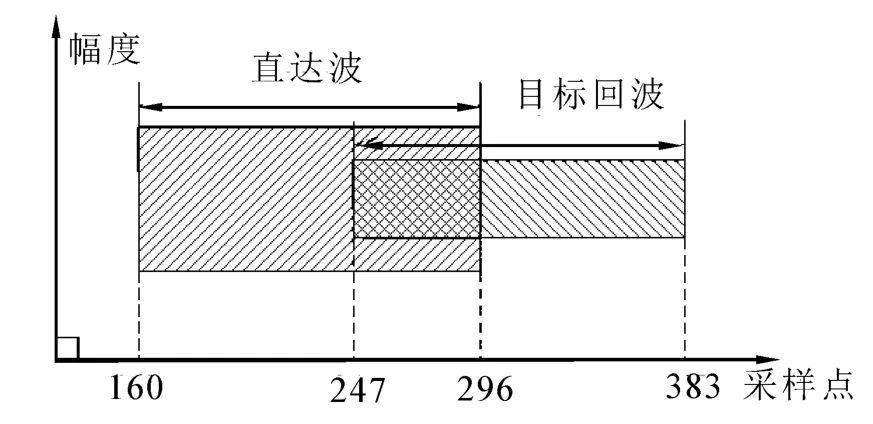
图9 直达波与目标回波示意图Fig.9 Sketch map of direct path wave and target echo
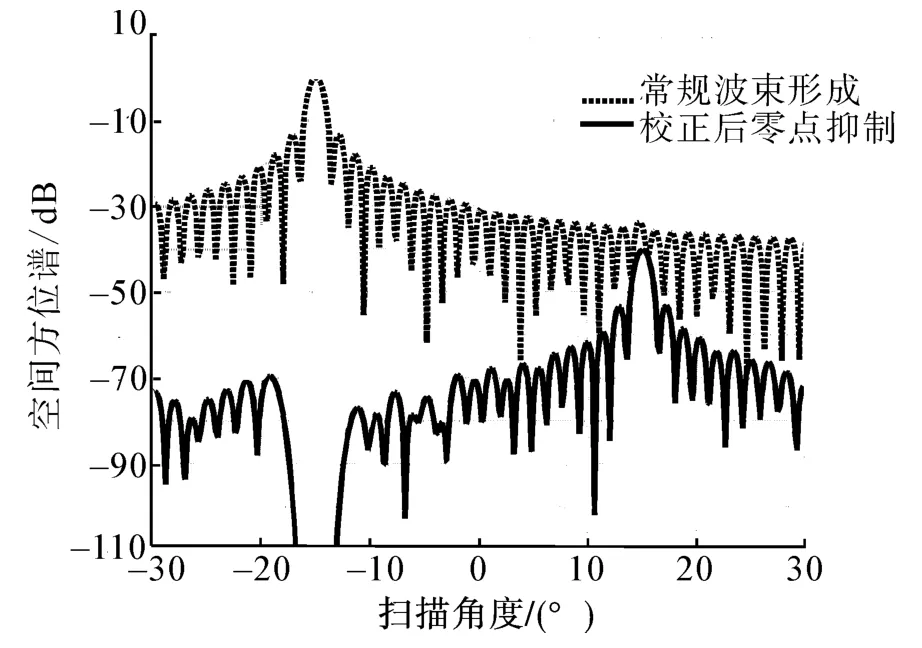
图10 直达波相位校正后的方位谱Fig.10 Spectrum with phase correction of direct path wave
由图10与图4(b)的对比可以看出,直达波相位校正后的零点约束算法在实际应用中有较好的宽容性,校正后的零点约束方位谱具有较好的主旁瓣比,直达波的旁瓣能够很好地被抑制,但前提是计算阵列校正误差的直达波direct2与目标回波信号中混有的直达波direct2具有相近的相位信息。
直达波的方位是对目标回波进行方位估计得到,由于直达波的高信噪比性,所以估计精度较高,根据直达波的方位得到直达波的理论阵列相位,并与只含有直达波信号的阵列相位比较得到校正相位。最后通过校正后的零点约束波束形成得到目标的方位。
4 水池实验结果
水池实验发射CW脉冲的频率为375 kHz,脉宽为T=1 ms。接收阵为等间隔线阵,阵元数为80,采样频率为137 kHz,采用带通采样。目标铅球的半径为6 cm,理论目标强度TS=-30.5 dB。试验中发射换能器、目标铅球、接收阵都悬挂于同一水平面处。水池试验的实际配置图与几何示意图分别如图11和图12所示。根据图12中水池配置的几何关系,可以计算出阵列的接收信号示意图如图9所示。试验中接收信号中只含有直达波的持续时间为160~246点,直达波和目标回波混叠的持续时间为247~296点。

图11 水池试验实际配置图Fig.11 Physical arrangements of tank experiment

图12 水池试验几何配置示意图Fig.12 Geometric arrangements of tank experiment
直达波与目标回波的入射角度分别为-15.6°和15.6°,直达波的能量比目标回波高40 dB,截取只含有直达波的信号,即160~246点,通过式(11)来计算阵列的校正相位Phase_corr。截取直达波和目标回波的混叠信号,即247~296点,在-17°~-13°的范围内设置6个零阶零点,进行零点约束直达波抑制。零点约束方位谱的输出响应如图13所示。
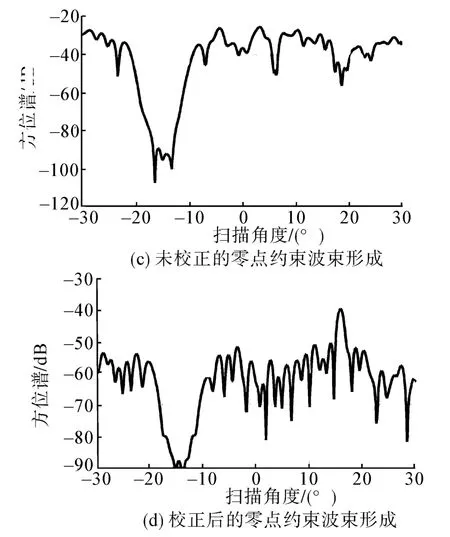
图13 直达波抑制的水池数据处理结果Fig.13 Data processing results of tank experiment
由图13可以看出:校正后的常规波束形成方位谱能够很好估计出直达波的方位,同时具有较好的旁瓣,与理想情况下的旁瓣近似,但由于直达波的能量比目标回波高出40 dB,目标回波的主瓣淹没在直达波的旁瓣中,只能估计出直达波的方位。在未进行阵列误差校正时,零点约束方位谱仍能够在直达波的主瓣附近产生零陷,但由于阵列存在相位误差,直达波旁瓣已将目标回波的主瓣淹没,目标的方位上无法形成波峰。而进行直达波相位校正过后,零点约束方位谱在直达波方向的附近产生零陷的同时能够很好地估计出目标的方位。且方位谱均用常规波束形成输出的最大值进行归一化,故目标回波峰值的能量与直达波的能量相差40 dB,这也与水池试验相吻合。
5 结束语
本文针对收发分置系统中的直达波抑制问题进行了分析。利用双基地中的直达波方位的先验知识和与目标回波信号的强相干性,给出了基于零点约束波束形成的直达波抑制方法。该方法在常规波束图的直达波方位附近加入了波束零点以达到直达波抑制的效果,运算量与常规波束形成近似,易于实现。但是由于零点约束波束对直达波相位的苛刻要求,导致算法对相位误差的宽容性很低,实际工程中很难满足。鉴于算法的这种缺陷,本文提出了基于相位校正的零点约束直达波抑制方法,该方法利用了直达波在短时间内的方位不改变的特性,先估计出直达波的方位,对阵列的相位进行校正,将信号中所含的直达波相位校正为理论的阵列相位后,再进行零点约束波束形成。通过水池实验可以看出基于直达波的相位校正提高了算法对相位的宽容性。
[1]CARUTHERS J W,NOVARINI J C.Modeling bistatic bottom scattering strength including a forward scatter lobe[J].IEEE Journal of Oceanic Engineering,1993,18(2):100-107.
[2]REED F A,LINDA Y,THAI P H.Spatial rejection of direct blast interference in multistatic sonars[P].United States.5425000,1995-07-13.
[3]李国君,唐小明,张财生.无源双基地雷达系统直达波抑制算法[J].火力与指挥控制,2012,37(1):32-35.LI Guojun,TANG Xiaoming,ZHANG Caisheng.Research on direct signal cancellation algorithm of passive bistatic radar[J].Fire Control and Command Control,2012,37(1):32-35.
[4]李辉,何友,周洪庆.外辐射源雷达系统中直达波干扰抑制技术[J].火力与指挥控制,2013,38(2):145-148.LI Hui,HE You,ZHOU Hongqing.Direct-path interference suppression in external illuminators-based radar system[J].Fire Control and Command Control,2013,38(2):145-148.
[5]ZHAO Bin,KONG Lingjiang,YANG Mei,et al.A directpath interference suppressing algorithm for shared-spectrum multistatic radar[C]//IEEE CIE International Conference on Radar.Chengdu,China,2011:929-932.
[6]朱家兵,洪一,陶亮.基于自适应分数延迟估计的FM广播辐射源雷达直达波对消[J].电子与信息学报,2007,29(7):1674-1677.ZHU Jiabing,HONG Yi,TAO Liang.Direct-path cancellation to FM broadcast transmitter radar based on adaptive fractional delay estimation[J].Journal of Electronics and Information Technology,2007,29(7):1674-1677.
[7]姚直象,惠俊英,蔡志明.矢量阵强相干干扰抑制技术研究[J].华中科技大学学报,2008,36(3):69-72.YAO Zhixiang,HUI Junying,CAI Zhiming.Suppressing strong coherent interference by acoustical vector sensor array[J].Journal of Huangzhong University of Science and Technology,2008,36(3):69-72.
[8]吴海洲,陶然,单涛.基于DTTB照射源的无源雷达直达波干扰抑制[J].电子与信息学报,2009,31(9):2034-2037.WU Haizhou,TAO Ran,SHAN Tao.Direct-path interference suppression for passive radar based on DTTB illuminator[J].Journal of Electronics and Information Technology,2009,31(9):2034-2037.
[9]肖红侠,项建弘.基于调零技术的相干干扰抑制方法[J].计算机应用研究,2013,30(6):1779-1782.XIAO Hongxia,XIANG Jianhong.Coherent interference suppression method for nulling technology[J].Application Research of Computers,2013,30(6):1779-1782.
[10]姚瑶,张明敏,袁骏.基于零陷展宽的双基地声呐直达波抑制算法[J].声学技术,2012,31(3):310-313.YAO Yao,ZHANG Mingmin,YUAN Jun.A direct path interference suppression algorithm of bistatic sonar based on null broaden method[J].Technical Acoustics,2012,31(3):310-313.
[11]LIU Hongming,LI Jun,HE Zishu.Clean algorithm based direct-path-nterference and multi-path interference suppression in bistatic MIMO Radar[C]//IEEE Microwave and Millimeter Wave Circuits and System Technology(MMWCST).Chengdu,China,2012:1-4.
[12]邹吉武.多基地声呐关键技术研究[D].哈尔滨:哈尔滨工程大学,2012:38-52.ZOU Jiwu.Study on multistatic sonar key technologies[D].Harbin:Harbin Engineering University,2012:38-52.
[13]Van TREES H L.Optimum array processing part IV of detection,estimation and modulation theory[M].New York:Wiley-Interscience,2002:120-127.
[14]刘斌,吴雄斌,徐全军.分布式高频地波雷达阵列幅相误差的校准方法[J].武汉大学学报:理学版,2012,58(3):269-274.LIU Bin,WU Xiongbin,XU Quanjun.A calibration of gain and phase errors for distributed HFSWR array[J].Journal of Wuhan University:Natural Science Edition,2012,58(3):269-274.
