具有学习效应的单机可控加工时间排序问题研究

王吉波,汪 佳,牛玉萍

(1.沈阳航空航天大学 经济与管理学院,沈阳 110136; 2.西安交通大学 机械制造系统工程国家重点实验室,西安 710053；3.沈阳航空航天大学 理学院,沈阳 110136)

具有学习效应的单机可控加工时间排序问题研究

王吉波1,2,3,汪 佳1,牛玉萍1

(1.沈阳航空航天大学 经济与管理学院,沈阳 110136; 2.西安交通大学 机械制造系统工程国家重点实验室,西安 710053；3.沈阳航空航天大学 理学院,沈阳 110136)

在经典排序问题中，工件的加工时间往往是一个常数，但在现代生产过程中，工件的加工时间受许多因素的影响。因此，研究工件具有学习效应的单机可控加工时间排序问题，其中工件的加工时间是其所在位置的函数，且与加工时间的控制变量有关。目标是求出最优的加工时间控制变量和最优的排序使得目标函数最小，目标函数包括极小化时间表长与控制费用的和、极小化总完工时间与控制费用的和、极小化总完工时间偏差和与控制费用和。证明他们都能转化为指派问题，从而多项式时间可解。并给出数值例子来说明问题是如何求解的。

学习效应；单机；排序；指派问题；控制变量

在经典的排序问题中，工件的加工时间通常是一个常数，但实际上在许多情况下工件的加工时间会随着学习效应、恶化效应或资源的分配等因素发生变化(Pinedo[1]，周伟刚等[2]，王吉波等[3]，王吉波等[4])。

带有学习效应的排序问题目前越来越受到人们的关注。学习效应产生的背景是，机器或人长时间加工相同或类似的工件时，他们的熟练程度会有所增加，导致后面加工的工件的加工时间会变小(Biskup[5])。关于学习效应的排序问题可以参考最新的综述论文Biskup[6]。Biskup[5]首次在排序中考虑学习效应因素，并假设工件的加工时间是其所在位置的函数，证明了在单机中极小化总加工时间和具有共同工期的极小化总完工时间是多项式可解的。Wang[7]考虑了工件具有学习效应的单机排序问题，其中假设工件的加工时间是其所在位置之前所有工件实际加工时间的函数，他们证明了极小化最大完工时间问题，总完工时间问题都是多项式可解的。Wang和Wang[8]研究了工件具有指数学习效应的流水作业排序问题，其中假设工件的加工时间是其所在位置的指数函数。对一些正则目标函数，他们给出了一些近似算法，并给出了最坏情况界。王吉波和刘璐[9]研究了工件具有学习效应和准备时间的单机排序问题，其中学习效应指的是任务的实际加工时间是该任务之前排好任务对数加工时间的递减函数。对目标函数为最小化总完工时间问题，他们提出了分支定界法和一个启发式算法。Wang等[10]研究了工件具有截断学习效应的单机排序问题，其中工件的加工时间是其所在位置和给定控制参数的函数。对一些正则和非正则目标函数，他们给出了多项式时间最优算法。Wang等[11]研究了工件具有截断学习效应的流水作业排序问题。对一些正则目标函数，他们给出了一些近似算法，并给出了最坏情况界，同时用数值模拟的方法说明了这些算法的好坏。

此外，对于加工时间可控的排序问题也被广泛的研究(Shabtay和Steiner[12]，Shabtay和Kaspi[13]，Wang和Wang[14])。关于加工时间可控的排序问题可以参考最新的综述论文Shabtay和Steiner[12]。最近的论文Wang和Wang[14]讨论了工件加工时间可控单机排序问题，其中工件的加工时间是所用资源的凸函数。他们对总加权流时间约束条件下极小化总资源费用的排序问题给出了分支定界算法和启发式算法。Wei等[15]讨论了工件加工时间与开工时间和所用资源都有关系的单机可控排序问题，其中工件加工时间是所用资源的线性递减函数。他们证明了两种多目标费用问题都能多项式时间解决，并给出了多项式时间算法。Wang和Wang[16]讨论了工件加工时间与开工时间和所用资源都有关系的单机可控排序问题，其中工件加工时间是所用资源的递减凸函数。他们证明了两种多目标费用问题都是多项式时间可解的。Wang等[17]讨论了工件加工时间与开工时间和所用资源都有关系(包括线性函数关系和凸函数关系)的单机成组排序问题。在每组的工件数相同情况下，他们证明了最大完工时间与所用资源的费用和问题可以多项式时间解决。

在另一方面一些文献研究了同时具有学习效应和资源分配的排序问题。Wang等[18]研究了加工时间依赖于学习效应和资源的单机排序问题。对两类目标函数，他们提出了多项式时间算法来求出最优排序和最优资源分配。此外，范雁鹏和赵传立[19]，王方和赵传立[20]研究了工件的实际加工时间具有学习效应与资源约束的单机排序问题，对一些与工期有关的非正则目标函数，他们给出了多项式时间算法。Lu等[21]研究了加工时间依赖于学习效应和资源的单机排序问题。对几类和工期有关的问题，他们提出了多项式时间算法来求出最优排序和最优资源分配。

本文从另外的角度研究工件加工时间具有学习效应的单机可控排序问题，该问题可将学习效应排序与加工时间可控的排序两类研究连接到一起。对三个不同的目标函数，即极小化时间表长和控制费用，极小化总完工时间和控制费用，极小化总完工时间偏差和和控制费用问题，我们证明这些问题都能够多项式时间求解。文章剩余部分安排如下：第二部分对问题进行描述，第三部分讨论了对于给定的排序找到最优的加工时间控制变量，第四部分通过将其转化为指派问题找到最优的排序，最后给出结论。

1 问题描述

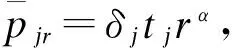
2 具有学习效应的最优加工时间控制变量的求解

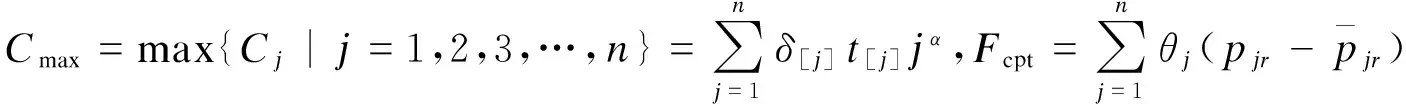
f(δ,π)=Cmax+Fcpt

(1)

其中[j]表示工件排在第j个位置。从以上等式我们可得到：对于给定的排序，1-θ[j]可以看作是加工时间控制变量的权，若1-θ[j]是负值，则δ[j]取最大值，若1-θ[j]是正值，则δ[j]取最小值，若1-θ[j]为零，则δ[j]取任意值，即δ[j]可表示为

(2)

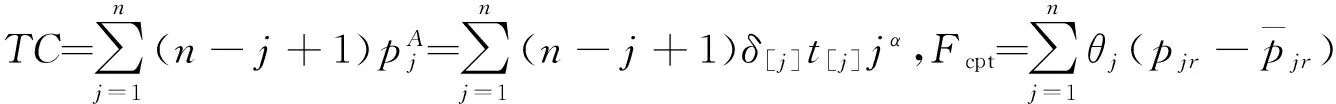
(3)

正如问题1|LE，CPT|Cmax+Fcpt中所得到的结论一样，同样的，对于给定的排序，我们将(n-j+1)-θ[j]看作是加工时间控制变量的权，若(n-j+1)-θ[j]是负值，则δ[j]取最大值，若(n-j+1)-θ[j]取正值，则δ[j]取最小值，若(n-j+1)-θ[j]为零，则δ[j]取任意值，即

(4)

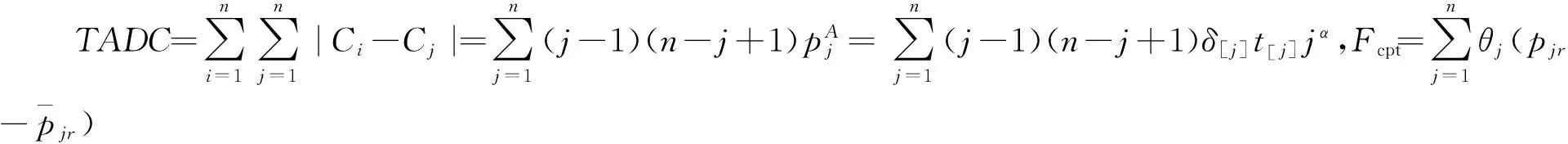
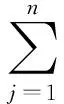
(5)

(6)

由以上分析，我们得到如下定理。

定理1 对于给定的排序π=(J[1],J[2],…,J[n]，最优的加工时间控制变量δ=(δ[1],δ[2],…,δ[n])的取得可以描述如下：如果加工时间控制变量的权是负值，则δ[j]取最大值，如果加工时间控制变量的权是正值，则δ[j]取最小值，如果加工时间控制变量的权是零，则δ[j]取任意值。即对于问题1|LE,CPT|Cmax+Fcpt，最优加工时间控制变量可由(2)得到；对于问题1|LE,CPT|TC+Fcpt，最优加工时间控制变量可由(4)得到；对于问题1|LE,CPT|TADC+Fcpt，最优加工时间控制变量可由式(6)得到。

证明 对于问题1|LE,CPT|Cmax+Fcpt，由(1)，对δ[j]求导得到t[j]jα(1-θ[j])，因此，当1-θ[j]<0，则δ[j]取最大值，若1-θ[j]>0，则δ[j]取最小值，若1-θ[j]=0，则δ[j]取任意值，即δ[j]可表示为：

3 最优排序的求解

对于问题1|LE,CPT|Cmax+Fcpt来说，我们需要找到最优的排序是使目标函数Cmax+Fcpt极小化，通过等式(1)，我们可以将其转化为指派问题求解最优的排序，令

(7)

(8)

则最优排序可转化为下面的指派问题求解：

(9)

xjr=0或1,j,r=1,2,3,…,n

其中第一个限制条件表示每个工件只能安排在一个位置上，第二个限制条件表示一个位置只能加工一个工件，第三个限制条件表示xjr为0-1变量，通过解此指派问题，我们即可求得问题1|LE,CPT|Cmax+Fcpt的最优排序。

同理,对于问题1|LE,CPT|TC+Fcpt，由式(3)，我们可以令

(10)

对于问题1|LE,CPT|TADC+Fcpt，由式(5)，我们可以令

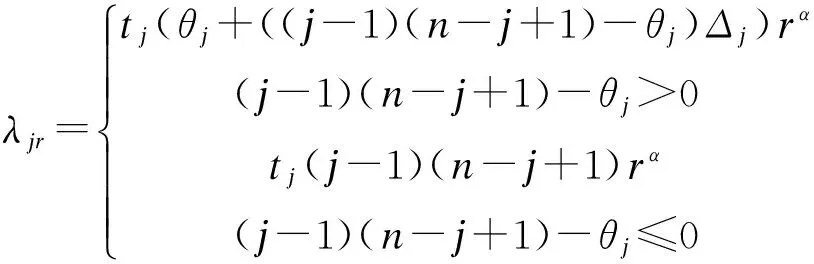
(11)

然后通过求解指派问题(9)，得到相应问题的最优排序。显然指派问题的时间复杂度为O(n3)。

清塘即清除池塘野杂鱼类，敌害生物，为苗种提供一个安全，舒适的环境。整塘就是将池水排干，清除池底和池边杂草。必须先整塘，曝晒数日后，再用药物清塘。选择的清塘药物一般为生石灰和茶麸，先用生石灰每亩80～100kg，要求加水融化后不待冷即向池中均匀泼洒；然后加注新水40～50cm；三日后用茶麸每亩30kg用水浸泡三四个小时后向池中均匀泼洒。

由以上分析我们可以给出问题1|LE,CPT|Cmax+Fcpt，1|LE,CPT|TC+Fcpt和1|LE,CPT|TADC+Fcpt的最优算法如下：

算法1

步骤1)：对于问题1|LE,CPT|Cmax+Fcpt，由公式(7)，计算λjr；对于问题1|LE,CPT|TC+Fcpt，由公式(10)，计算λjr；对于问题1|LE,CPT|TADC+Fcpt，由公式(11)，计算λjr。

步骤2)：解决指派问题(9)，得到相应问题的最优排序。

步骤3)：由定理1，对于问题1|LE,CPT|Cmax+Fcpt，最优加工时间控制变量可由(2)得到；对于问题1|LE,CPT|TC+Fcpt，最优加工时间控制变量可由(4)得到；对于问题1|LE,CPT|TADC+Fcpt，最优加工时间控制变量可由(6)得到。

显然，算法1的时间复杂度为O(n3)(主要步骤由指派问题决定)。因此我们有

定理2 算法1能够求得问题1|LE,CPT|Cmax+Fcpt，1|LE,CPT|TC+Fcpt和1|LE,CPT|TADC+Fcpt，的最优排序和最优加工时间控制变量，时间复杂度为O(n3)。

我们给出下面的例子来说明算法1是如何实现的(我们只考虑问题1|LE,CPT|Cmax+Fcpt)。

例1 对于问题1|LE,CPT|Cmax+Fcpt,n=4,α=-0.5,t1=1,t2=2,t3=3,t4=4,θ1=1,θ2=2,θ3=0.5,θ4=3,Δ1=0.5,Δ2=1/3,Δ3=1/4,Δ4=1/5

1-θ1=0δt=[1/2,1]1-θ2=-1δ2=11-θ3=0.5δ3=1/41-θ4=-2δ4=1λ11=1λ21=2λ31=1.875λ41=4λ12=1λ22=2λ32=1.875λ42=4λ13=0.58λ23=1.15λ33=1.08λ43=2.31λ14=0.5λ24=1λ34=0.94λ44=2

通过指派问题求得x11=x23=x32=x44=1，所以最优的排序为[J1,J3,J2,J4]，最优的加工时间控制变量为δ1=[1/2,1]，δ2=1，δ3=1/4，δ4=1，极小化的目标函数为f(δ,π)=Cmax+Fcpt=5.48。

4 结论

本文主要研究了工件具有学习效应的单机可控加工时间排序问题，在此主要讨论了三个不同的目标函数，即极小化最大完工时间与控制费用和，极小化总完工时间与控制费用和，极小化总完工时间偏差和与控制费用和，通过将其转化为指派问题，从而证明这些问题多项式时间可解，即能够以多项式时间求得问题的最优的加工时间控制变量和最优排序。在未来的研究中我们希望将其推广到平行机或流水作业排序中，或目标函数可以考虑更多的因素，比如准时制排序问题等。

[1]Pinedo M.Scheduling:Theory,Algorithms,and Systems[M].Upper Saddle River,NJ:Prentice-Hall,2002.

[2]周伟刚,冯倩倩,高成修.加工时间可控和恶化的单机最大完工时间排序[J].应用数学学报,2012,35(4):617-625.

[3]王吉波,王建军,何平.具有共同松弛时间的恶化型工件排序问题研究[J].大连理工大学学报,2012,52:932-936.

[4]王吉波,刘璐,许扬涛,等.具有恶化工件的不同工期指派问题研究[J].沈阳航空航天大学学报,2013,30(5):83-87.

[5]Biskup D.A state-of-the-art review on scheduling with learning effects[J].European Journal of Operational Research,2008,188:315-329.

[6]Biskup D.Single machine scheduling with learning considerations[J].European Journal of Operational Research,1999,115:173-178.

[7]Wang J-B.Single machine scheduling with a sum of actual processing time based learning effect[J].Journal of the Operational Research Society,2010,61:172-177.

[8]Wang J-B,Wang M-Z.Worst case analysis for flow shop scheduling problems with an exponential learning effect[J].Journal of the Operational Research Society,2012,63:130-137.

[9]王吉波,刘璐.带准备时间的任务单机学习效应排序问题[J].大连理工大学学报,2013,53(6):930-936.

[10]Wang X-R,Jin J,Wang J-B,Ji P.Single machine scheduling with truncated job-dependent learning effect[J].Optimization Letters,2014,8:669-677.

[11]Wang X-Y,Zhou Z,Zhang X,Ji P,Wang J-B.Several flow shop scheduling problems with truncated position-based learning effect[J].Computers & Operations Research,2013,40:2906-2929.

[12]Shabtay D,Steiner G.A survey of scheduling with controllable processing times[J].Discrete Applied Mathematics,2007,155:1643-1666.

[13]Shabtay D,Kaspi M.Minimizing the total weighted flow time in a single machine with controllable processing times[J].Computers & Operations Research,2004,31:2279-2289.

[14]Wang J-B,Wang M-Z.Single-machine scheduling to minimize total convex resource consumption with a constraint on total weighted flow time[J].Computers & Operations Research,2012,39:492-497.

[15]Wei C-M,Wang J-B,Ji P.Single-machine scheduling with time-and-resource-dependent processing times[J]Applied Mathematical Modelling,2012,36:792-798.

[16]Wang X-R,Wang J-J.Single-machine scheduling with convex resource dependent processing times and deteriorating jobs[J].Applied Mathematical Modelling,2013,37:2388-2393.

[17]Wang D,Huo Y,Ji P.Single-machine group scheduling with deteriorating jobs and allotted resource[J].Optimization Letters,2014,8:591-605.

[18]Wang D,Wang M-Z,Wang J-B.Single machine scheduling with learning effect and resource dependent processing times[J].Computer & Industrial Engineering,2010,59:458-462.

[19]范雁鹏,赵传立.带有交货期和加工时间可控的单机排序问题[J].重庆师范大学学报：自然科学版,2013,30(3):5-8.

[20]王方,赵传立.具有学习效应且加工时间可控的单机排序问题[J].沈阳师范大学学报：自然科学版,2013,31(4):471-475.

[21]Lu Y-Y,Li G,Wu Y-B,Ji P.Optimal due-date assignment problem with learning effect and resource-dependent processing times[J].Optimization Letters,2014,8:113-127.

[22]Kanet JJ.Minimizing variation of flow time in a single machine systems[J].Management Science,1981,27:1453-1459.

(责任编辑：赵金兰 英文审校：刘敬钰)

Asinglemachineschedulingwithlearningeffectandcontrollableprocessingtimes

WANG Ji-bo1,2,3,WANG Jia1,NIU Yu-ping1

(1.School of Economics and Management,Shenyang Aerospace University,Shenyang 110136,China;2.State Key Laboratory for Manufacturing Systems Engineering,Xi′an Jiaotong University,Xi′an 710053,China;3.School of Science,Shenyang Aerospace University,Shenyang 110136,China)

In classical scheduling,the processing time of a job is a constant,but in modern production process,the processing time of a job is affected by many factors.Hence,in this paper we study scheduling problems jobs with learning effect and controllable processing times,where the processing time of a job is the function of its position in a sequence and its controllable variable.Our target is to find the optimal sequence and controllable variables so as to minimize the following objective functions:a cost containing makespan and total controllable cost,a cost containing total completion time and total controllable cost,a cost containing total absolute differences in completion times and total controllable cost.We prove that the problem is modeled as an assignment problem,and thus can be solved in polynomial time.We also give a numerical example.

learning effect;single machine;scheduling;assignment problem;controllable variable

2014-07-11

国家自然科学基金项目(项目编号：11001181)； 机械制造系统工程国家重点实验室开放课题(项目编号：sklms201306)

王吉波(1975-),男,辽宁沈阳人，博士后,教授,大连理工大学博士生导师(兼职)，主要研究方向：生产计划与排序，E-mail：wangjibo75@163.com。

2095-1248(2014)05-0082-05

O223；C934

A

10.3969/j.issn.2095-1248.2014.05.016