基于改进小波变换和包络分析的滚动轴承故障诊断

张 强，沙云东，梁先芽，赵奉同，栾孝驰

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

基于改进小波变换和包络分析的滚动轴承故障诊断

张 强，沙云东，梁先芽，赵奉同，栾孝驰

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

采用改进的小波分解和重构算法与包络分析相结合的方法，提取滚动轴承振动信号的故障特征频率。改进的小波分解和重构方法避免了Mallat算法频率混淆的缺陷，通过对重构信号特定频带进行包络分析，更加准确地提取了滚动轴承的故障特征频率。通过对无故障滚动轴承和内圈、外圈有故障的滚动轴承振动信号的分析，说明这种方法能够有效诊断滚动轴承的故障，并将该方法成功应用于某型航空发动机主轴承故障诊断。

滚动轴承；故障诊断；小波变换；包络分析

航空发动机主轴轴承是航空发动机的重要部件，其工作环境苛刻，引起轴承失效的因素也非常复杂。航空发动机在高速、重载等复杂环境条件下工作，主要失效形式有磨损、塑性变形、疲劳剥落、整体损坏(例如保持架的损坏)4种类型[1]。滚动轴承故障信号的处理方法主要有小波变换[2-3]、EMD分析、盲源分离等。小波变换具有带通滤波特性，选择合适的小波对信号进行适当尺度的分解，选择有价值的频段进行重点分析。包络分析[4]在滚动轴承故障诊断中也被普遍认可，提取能够反映轴承真实故障的特征频率成分，作为判定滚动轴承是否正常的标准。本文采用小波变换与包络分析相结合的方法，提取故障特征频率，对滚动轴承进行故障诊断。

1 小波变换理论[5-9]及其改进

小波变换为信号分析提供了一种更加精细的方法，通过将信号按频带进行多层分解，根据信号各频率f成分的能量分布，确定重点分析频带，从而提高了分析的针对性和准确性，在滚动轴承故障诊断中具有很高的应用价值。

Mallat算法作为正交小波的快速算法，提供了一种非常便捷的手段。Mallat算法是二进离散小波变换的快速算法，其分解公式为：

Ao[f(t)]=f(t)

(1)

式中：t=1，2，…,N；j=1，2，…，J；J=log2N；h和g为正交镜像滤波器。

通过(1)式的分解，信号f(t)被分解成高频部分Dj(细节部分)和低频部分Aj(近似部分)。分解过程中，分别与正交镜像滤波器h和g卷积和隔点采样。每次分解都进行一次隔点采样，所以分解的过程也是频带二分的过程。Mallat算法重构公式为：

(2)

式中：j=J-1，J-2，…，1，0；J=log2N；t=1，2，…，N；H和G为正交镜像滤波器。

信号与非理想的实际正交滤波器进行卷积运算后，高频成分混入相邻的低频带中，隔点采样过程因不满足采样定理导致频率混叠。文献[10]提出一种小波分解与重构的快速算法。本文采用改进的小波变换结合快速Fourier变换，克服了Mallat算法的缺陷，具体做法是：

(1)消除取得Aj过程的频率混淆的方法

b:对FFT变换中频率大于fs/2j+1部分频率值置零；

c:对置零后的结果进行IFFT变换；

d:对IFFT变换结果隔点采样，其结果作为Aj用于下一步分解；

(2)消除取得Dj过程的频率混叠的方法

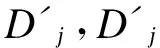
b:对FFT变换中频率f≤fs/2j+1部分频率值置零；

c:对置零后的结果进行IFFT变换,结果作为Dj,不进行隔点采样；

(3)消除Aj重构过程频率混淆的方法

消除近似部分Aj重构过程中频率混叠的方法是在第2j尺度上，由未被隔点采样的信号开始重建，在2j尺度上不进行隔点插零，从下一步即第2j-1尺度上进行隔点插零，由于第一步重构过程不产生虚假频率成分，而后续的虚假成分又被频宽倍增的H滤掉，因此就消除了Aj重建过程的频率混淆；

(4)消除取得Dj过程的频率混叠的方法

a:设dj是由Dj重构的结果，对dj进行FFT变换；

b:FFT变换过程中非[fs/2j+1,fs/2j]部分频率值置零；

c:对置零后的结果进行IFFT变换，结果即为真实的dj。

2 包络解调法

包络解调法是故障诊断常用的一种方法，主要用来分析调制信号，可非常有效地识别某些冲击信号。包络解调是一种基于滤波检波的信号处理方法，对高频共振信号进行检波处理后，从高频载波中提取附在高频载波信号的低频信号。常用的包络解调分析方法宽带解调技术、共振解调技术、Hilbert解调技术等。本文利用Hilbert解调技术对小波重构信号进行分析。

Hilbert[11-14]变换揭示了由Fourier变换联系的时域和频域之间的一种等价互换关系，其与Fourier变换的对称性质有紧密联系。

假设x(t)是连续信号，其Hilbert变换为

(3)

由x(t)及其Hilbert变换可构成信号x(t)的解析信号z(t)

(4)

幅值为

(5)

由(5)式可求出f(t)的包络。对包络信号作Fourier变换，得到信号的包络谱。由该方法的解调功能，一般对易受干扰的低频成分提取非常有效，提高了滚动轴承故障诊断的准确性。

3 基于小波变换和包络分析的滚动轴承故障诊断

滚动轴承的常见故障有剥落、断裂、塑性变形、磨损、腐蚀和胶合等。当滚动轴承的工作表面出现局部缺陷，就会以一定的频率产生一系列的宽带脉冲，称这一频率为滚动轴承故障的特征频率。在滚动轴承的故障诊断中就是利用了故障的特征频率。

滚动轴承各元件的故障特征频率计算公式：

1)z个滚动体与外圈某故障点接触的频率：

(9)

2)z个滚动体与内圈某故障点接触的频率：

(10)

3)滚动体上某点与外圈接触的频率：

(11)

假设外圈固定，内圈(即轴)的转频为fs，轴承节径为D，滚动体直径为d，接触角为α，滚动体个数为z，并假定滚动体与内圈和外圈之间纯滚动。

3.1 试验方法应用研究

采用美国Case Western Reserve University电气工程实验室的滚动轴承故障模拟实验台的故障数据进行诊断分析[15]。试验中采用6205-2RS JEM SKF型轴承，转速为1 797 r/min，滚动体个数为9，轴承参数见表1。

表1 6205-2RS JEM SKF型轴承参数 mm

由故障特征频率公式和轴承参数，计算6205-2RS JEM SKF型滚动轴承各元件的故障特征频率，见表2。

数据分析及结果如下所示：

(1)首先对无故障轴承和外圈故障轴承时域信号及其频谱进行对比，如图1和图2与图3和图4所示，分析故障轴承的频率分布特点，对于滚动轴承的外圈故障，频率主要分布在2～4 kHz之间。此外，故障轴承信号的幅值远远高于正常轴承幅值。

表2 轴承元件的故障特征频率f Hz

图1 无故障轴承时域信号

图2 无故障轴承频谱

图3 外圈故障轴承时域信号

图4 外圈故障轴承信号频谱

(2)采用db10小波对外圈故障轴承信号进行三层小波分解，依据原始信号频谱的频率成分分布特点，对第二层细节部分(1.5～3 kHz)进行包络分析，图5为重构第二层细节部分时域信号及其频谱，图6为第二层细节部分的包络谱。包络谱中清晰的显示了110 Hz的频率成分及其倍频谱线，与理论计算的外圈故障特征频率107 Hz非常接近，故由提取出的频率成分判断轴承外圈存在故障，与滚动轴承实际存在故障相符。

图5 第二层细节部分时域信号及其频谱

图6 第二层细节部分包络谱

3.2 航空发动机主轴承故障诊断试验分析

针对某型航空发动机台架试验过程中发生故障报警现象，怀疑是主轴轴承存在故障。为此，在地面检验的条件下对某型涡扇发动机进行故障诊断，采集试验数据并记录发动机的工作状态及相关数据，并分析和处理，对该型发动机主轴轴承进行故障诊断。

某型发动机高压涡轮后轴承的基本参数为：z=34个，直径为Db=8 mm的滚棒组成的轴承，其轴承节圆直径为Dc=148 mm，接触角为β=0°，外圈半径为140 mm,内圈半径为111 mm。地面试验过程中，发动机在低压转子驱动器的驱动下保持转速为fr=120 r/min的稳态过程,试验过程中外圈转速视为零。计算得故障特征频率：外圈32 Hz，内圈36 Hz，滚棒18 Hz。

试验采用LMS数据采集系统，采样频率为1 024 Hz，测试转速为120 r/min。传感器分别安装在距离主轴承位置最接近的机匣水平和垂直位置，测量振动加速度信号。

某型航空发动机地面试验数据分析：

分别对发动机机匣某截面水平和垂直测点的振动信号分析，限于篇幅，本文仅对某截面水平测点信号进行分析，如图7所示。观察频谱中各频率成分的分布规律，如图8，频谱中观测到0～150 Hz频带中频率成分峰值最大，表示该频段蕴含故障特征可能性最大，据此确定三层小波分解已满足分析要求，对0～150 Hz(第二层近似部分)进行重点分析。如图9所示。对第二层近似部分包络分析，再作Fourier变换，得到第二层近似部分包络谱，图10中清晰显示31.8 Hz及其倍频的频率成分，与理论计算的外圈故障特征频率相一致，机匣垂直位置信号分析得到相同的结果，从而确定发动机主轴承外圈存在故障。

图7 机匣水平位置振动实测数据

图8 振动信号频谱

图9 小波分解第二层近似部分重构信号及其频谱

图10 第二层近似部分包络谱

4 结论

针对航空发动机主轴承故障测试信号传递路径复杂，干扰信号多，故障信号微弱的特点，本文采用改进的小波变换与包络分析相结合的方法对混入复杂信号的瞬态微弱冲击信号进行分析并取得理想结果:(1)改进的Mallat算法，消除了传统单子带重构过程中的频率混淆，提高了信号分析的准确性;(2)采用改进的小波分解与重构算法和包络分析相结合的方法，有效地提取了滚动轴承故障特征频率，为准确诊断航空发动机主轴承故障诊断提供了一种有效的方法，具有重要的工程意义。

[1]Hingley C S.Rolling contacts four ways failure.Power Transmission Design,1970,12(3):55-59.

[2]林京.连续小波变换及其在滚动轴承故障诊断中的应用[J].西安交通大学学报,1999,33(11):108-110.

[3]程军圣,于德介,邓乾旺,等.连续小波变换在滚动轴承故障诊断中的应用[J].中国机械工程,2003,14(23):2037-2040.

[4]吴益峰,汤伟.基于小波变换的高速纸机滚动轴承故障诊断[J].计算机测量与控制,2010,(6):1256-1259.

[5]史东锋,鲍明,屈梁生.小波包络分析在滚动轴承诊断中的应用[J].中国机械工程,2000,11(12):1382-1385.

[6]Mallat S.A theory for multi-resolution signal decomposition：the wavelet representation.IEEE Trans.on Patern analysis and Machine Intelligence，1989,1l(7)：574-69.

[7]Daubeehies I.Orthonornal bases of compactly supported wavelets[M]．Conlnl Pure and Appl Math，1988:41.

[8]崔锦泰.小波分析导论[M].西安:西安交通大学出版社,1995:161-229.

[9]沈金伟,石林锁.滚动轴承故障诊断的改进小波变换谱峭度法[J].轴承,2010,(8):46-49.

[10]杨建国,夏松波，须根法.小波分解与重建中产生频率混淆的原因与消除算法[J].哈尔滨工业大学学报,1999，31(2)：61-64.

[11]张盈盈，潘宏侠.基于小波包和Hilbert包络分析的滚动轴承故障诊断方法[J].电子测试,2010，(6)：20-23.

[12]赵玉菊.基于小波变换和包络分析的铁路货车滚动轴承故障诊断研究[D].石家庄铁道学院,2006：24-34.

[13]史东锋,鲍明,屈梁生.小波包络分析在滚动轴承诊断中的应用[J].中国机械工程,2000,11(12):1382-1385.

[14]荆强,向敬忠,时献江.基于小波变换和实调制细化包络谱的滚动轴承故障诊断[J].科技资讯,2010,(11):46-48.

[15]The Case Western Reserve University Bearing Data Center Website.Bearing data center seeded fault test data[EB/OL].[2007-11-27].http://www.eecs.cwru.edu/la boratory/bearing/.

(责任编辑：宋丽萍 英文审校：刘敬钰)

Faultdiagnosisofrollingbearingbasedonimprovedwavelettransformandenvelopeanalysis

ZHANG Qiang，SHA Yun-dong，LIANG Xian-ya，ZHAO Feng-tong，LUAN Xiao-chi

(Liaoning Key Laboratory of Advanced for Aeronautical Propulsion Test Technology,Shenyang Aerospace University,Shenyang 110136，China)

Fault characteristic frequency components of rolling bearing vibration signals were extracted by the method of combining an improved wavelet decomposition and reconstruction algorithm and envelope analysis.The improved wavelet decomposition and reconstruction approach avoids the defects of Mallat algorithm′s confusion in frequencies.Extracting the rolling bearing fault characteristic frequencies are more accurate.Analysis of normal rolling bearing and inner ring and the outer ring failure rolling bearing vibration signals indicate that the method can effectively diagnose the fault of rolling bearings.Furthermore,using this method succeeded in diagnosing the faults of aero-engine main bearings.

rolling bearing;faults diagnosis;wavelet transform;envelope analysis

2013-08-28

张强(1986-)，男，山东淄博人，硕士研究生，主要研究方向：航空发动机强度、振动及噪声，E-mail:zhangqiang413@163.com； 沙云东(1966-)，男，黑龙江阿城人，教授，主要研究方向：航空发动机强度、振动及噪声，E-mail:ydsaha2003@vip.sina.com。

2095-1248(2014)05-0012-05

TH133.3;V233.1

A

10.3969/j.issn.2095-1248.2014.05.003