精密同轴回转式测量机构模态分析及优化

金 印,杜乐普，2，石 宏，刘明明

(1.沈阳航空航天大学 航空宇航工程学部(院),沈阳 110136; 2.空军石家庄飞行学院 第一训练旅,河北 石家庄 050081)

精密同轴回转式测量机构模态分析及优化

金 印1,杜乐普1，2，石 宏1，刘明明1

(1.沈阳航空航天大学 航空宇航工程学部(院),沈阳 110136; 2.空军石家庄飞行学院 第一训练旅,河北 石家庄 050081)

在完成对某同轴回转式测量系统中回转装置的初期设计基础上，对其中回转装置进行模态分析，结果显示回转装置第一阶模态频率偏低，为避免其与检测现场激振频率发生共振，并提高检测精度，提出采用Workbench中灵敏度分析的方法，对回转装置结构进行优化，得到了回转装置的最佳设计方案。研究结果对提高系统精度，防止共振的发生等方面具有重要意义，为进一步的设计改进工作提供很好的理论支持。

回转体；模态分析；优化设计；灵敏度分析

近些年来，随着振动理论和结构分析理论的发展，先进的测试手段和分析技术不断出现，相关CAD、CAE软件的应用，使得能够应用动力学模型对机械结构进行详尽、系统的分析，对于产品的设计在设计阶段就能较好地完成结构的动力学优化[4]。

航空发动机大修时发现涡轮机匣由于工作环境问题造成变形，导致涡轮机匣外环与转子装配后同心度降低，造成涡轮机匣外环与转子间叶尖间隙不符合设计要求。从而导致航空发动机效率下降，甚至转子叶片叶尖与机匣外环碰磨等不良现象时有发生。进行修理维护前，不仅要对涡轮机匣外环中心与转子中心的同心度进行检测，而且要对涡轮机匣外环内壁上各点相对转子中心的准确半径进行检测，确定碰磨发生位置。如图1所示的同轴回转式测量设计简图，测量机构通过定心标准件保证立柱与被测工件基准回转轴线同轴，通过磁力吸盘固定在工作平台之上，传感器沿L型标尺滑动到与被测工件接触后锁死。开始测量时，由低速电机带动L型标尺与传感器测头围绕立柱做回转运动，基于其检测原理，其检测精度很大程度上取决于检测机构受力变形后导致传感器的位置变化精度，尤其是在检测方向上传感器的相对位置变化，由于本检测系统是在现场进行的在线式检测。所以，即使检测系统的隔振效果做的再好，回转装置仍旧会在现场振动的激励频率下引起振动，而这将会引起传感器的位置变化，影响最终的检测精度。另一方面，由于系统采用的是360°的扫描式检测，内部部件的运动也会对检测精度造成影响[4]。

为了减少回转装置的固有频率、模态振型等对系统检测精度的影响，合理地设计回转装置尺寸，对回转装置进行模态分析，并采用有限元软件中的灵敏度分析对回转装置进行结构参数优化设计，寻求更加适合工作环境的回转装置结构，以保证整个检测系统的检测精度。

图1 同轴回转式测量设计简图

1 模态分析

1.1 模态分析理论

通过模态分析方法可以搞清楚结构在某一受影响的频率范围内的各阶主要模态。模态分析的作用有以下3个方面：1)使结构避免共振或按特定频率进行振动；2)了解结构对不同类型的动机载荷的响应；3)有助于在其他动力学分析中估算求解控制参数[3]。模态分析的控制方程为：

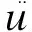
(1)

式中，[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{u}为位移向量，F(t)为作用力，t为时间

当作用力F(t)=0时，忽略阻尼的影响可以得到无阻尼结构自由振动方程，即

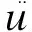
(2)

如果令{u}={φ}θjwt,代入式(2)可得结构振动特征方程：

([K]-w2[M]){φ}=0

(3)

当作用力F(t)=F时，忽略阻尼的影响，可以得到考虑应力影响的振动方程：

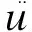
(4)

对式(4)做傅里叶变换得：

(5)

由式(3)或式(5)即可求出特征值wi和特征向量{φi}，进一步可解得固有频率和振型。

1.2 基于有限元的回转装置模态分析

回转装置材料属性：弹性模量为200 GPa；泊松比为0.3；密度为7.8×107kg/m3。

根据回转装置的结构特点，对模型中的螺栓、螺母等配件实行简化，建立如图2所示其在工作位置时的实体模型。在有限元软件中采用六面体网格划分，节点数20 216，单元数5 236。对模型求解前6阶模态，结果如表1所示。

图2 回转装置实体简图

由于本检测系统是在现场进行的在线式检测。所以，即使检测系统的隔振效果做的再好，回转装置仍旧会在现场振动的激励频率下引起振动，而这将会引起传感器的位置变化，影响最终的检测精度。由表2可以看出，第一阶模态频率偏低，为避免与现场低频率激励发生共振，提高检测系统精度，采用灵敏度分析法，在保证检测系统精度的前提下，主要提高一阶模态频率对回转装置进行结构优化。

表1 回转装置前6阶模态频率

2 结构特性的灵敏度分析方法

所谓结构特性的灵敏度分析就是在结构设计的过程中，结构的数学模型确定之后，经常会遇到两种情况需要对结构要做一定的修改。其一是由于结构设计与制造装配的原因，要对结构做一些局部的微调；其二是为了使结构的动静态特性满足某项技术指标的要求[1]。就算是一个很简单的结构，也有很多种修改方法可以选择，有很多设计参数可以调整。为了确定哪种方案最为适合检测要求，分析各个设计变量或结构参数的改变对检测结构的动静态特性变化的灵敏程度势在必行。本文采用有限元方法对回转装置进行动静态计算，并结合有限元分析软件优化设计模块对回转装置的设计参数进行了灵敏度分析。这里采用的梯度工具是有限差分法[1]。

有限差分法分为向前差分、向后差分和中心差分3种方法。有限差分法的基本做法是使设计变量有一微小摄动，通过结构分析求出结构形态，再由差分格式来计算约束函数y(x)关于设计变量X的近似导数[2]，一种简单的方法是采用向前差分格式：

(6)

式中Xi=(x1,x2,…,xi+Δxi,…,xn)T，式(6)的截断误差与Δxi同阶，向后差分的方法表示为：

(7)

式中xi-=(x1,x2,…x1-Δxi,…,xn)T，式(7)的截断误差与Δxi同阶，有时采用更为精确的中心差分公式：

(8)

3 回转装置的优化设计

3.1 回转装置的灵敏度分析

根据回转装置的结构特征，选择了6个设计参数x1～x6，设计参数模型如图3所示。

图3 回转装置设计参数模型

在建立完参数化模型的基础上，运用基于中心差分法对回转装置的设计参数进行了分析，得到了回转装置设计参数对一阶模态频率的梯度信息，获得了设计参数变化的灵敏度信息，从而提取了最佳的设计参数，灵敏度分析曲线如图4所示。

由图4可知，最开始选择的6个参数并不是都对目标函数敏感，根据灵敏度分析的结果，可以提取出4个最佳的设计参数x1,x2,x3,x4。

3.2 优化设计的数学模型

根据设计要求确定回转装置的优化设计模型为：求设计变量X=[x1,x2,x3,x4]T的值，使一阶模态频率Freq→max

满足：xmin≤xf≤xmax，i=1,2,3,4

Delta≤0.06 mm，smax≤1.3 MPa

其中，xmin，xmax为设计变量的上、下限值,Delta为最大变形,为节点的最大应力。

图4 设计参数对一阶模态频率的灵敏度分析结果

3.3 优化设计结果

在建立完数学模型后，采用有限元软件对回转装置进行优化设计，得到了其优化设计的结果。一阶模态频率、最大变形以及应力随设计参数变化趋势如图5所示。回转装置的初始设计方案与最优设计方案比较，如表2所示。从优化结果可以看出优化设计后的一阶固有频率提高了11.96 Hz。该方案满足了所有状态变量的要求，并且使得回转装置的一阶固有频率有较大的提高。

图5 一阶模态频率随设计参数变化趋势

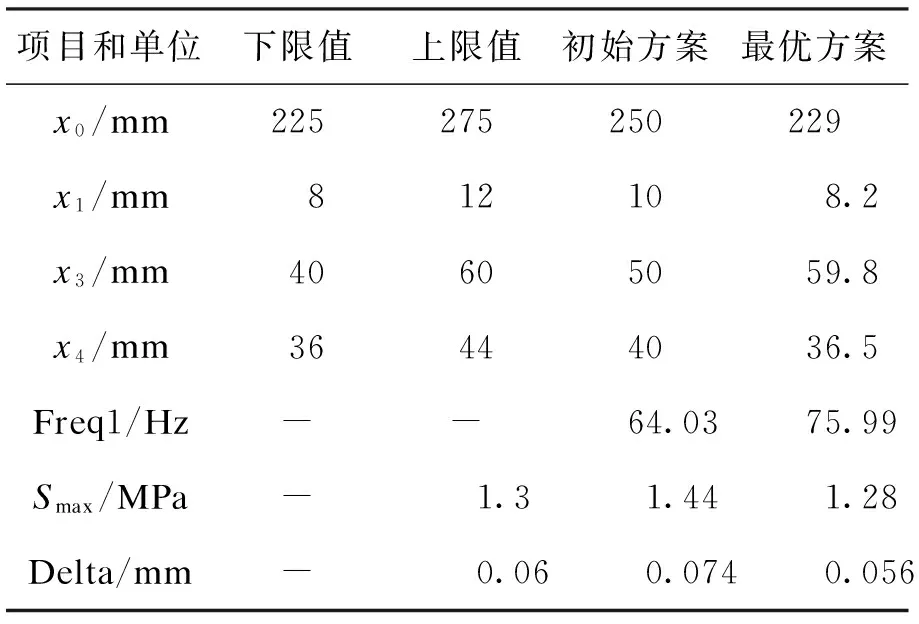
表2 回转装置的初始设计方案与优化设计方案比较

4 结论

采用有限元软件，对同轴回转式测量中回转装置进行了模态分析，得到了回转装置的前6阶模态。从优化结果可以得出，在满足目标函数要求的前提下，回转装置的一阶模态频率提高了11.96 Hz，而且最大变形以及应力值低于初始设计，这样不仅避免了与现场主要激振频率发生共振，而且提高了整个检测系统的精度。

[1]夏丹，刘军考.基于灵敏度分析的精密离心机负载盘的优化设计[J].机械设计，2006，11.

[2]张旭明，王德信.结构灵敏度分析的解析方法[J].河海大学学报，1998，26:44-49.

[3]买买提明·艾尼，陈华磊.ANSYS Workbench 14.0仿真技术与工程实践[M].清华大学出版社，2013:66-67.

[4]周俊峰，谭建平.高精度薄板带板凸度激光检测的误差分析与精度控制研究[D].长沙：中南大学,2006:60-69.

[5]Mroz,Z.Shape and topology sensitivity analysis and its application to structural design[J].Archive of Applied Mechanics,2012(10):1541-1555.

[6]宋强云，方宗德.直升机一体化齿轮轴的模态分析及优化[J].机械设计与制造，2008(10):152-153.

[7]Bakshi P，Pandey P C.Analytical response sensivity using hybird finite elements[J].Comp.andStruct,2000(70):281-297.

[8]丁伟，丁渭平.装载机驾驶室试验模态分析及动态特性优化[J].机械设计与制造，2013(11):231-234.

[9]Ramakrishnan CV，Francavilla A.Structural shape optimization using penalty functions[J].J.Stuch.Mech,1974(3)：403-422.

[10]Wang S Y，Sun Y，Gallagher R H.Sensitivity analysis in shape optimization of continuum structures[J].Comp.and Stuct,1985(20):855-867.

[11]曹树谦，张文德，萧龙翔.振动结构模态分析[M].天津：天津大学出版社，2002:1-3.

[12]高云凯.轿车车身结构修改灵敏度分析[J].汽车工程，2007(6):511-514.

[13]崔岸.基于模态灵敏度分析的商用车驾驶室结构优化[J].汽车工程，2010.

[14]沃德·海伦，斯蒂芬·拉门兹.模态分析理论与试验[M].北京：北京理工大学出版社，2001:241-244.

[15]Kibsgaard S.Sensitivity analysis the basis for optimization.Int J Num Mech Eng，1992(34):901-932.

(责任编辑：宋丽萍 英文审校：刘敬钰)

Modalanalysisandoptimaldesignfortheprecisioncoaxialrotarymeasuringmechanism

JIN Yin1，DU Le-pu1,2，SHI Hong1，LIU Ming-ming1

(1.Faculty of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China; 2.The First Training Brigade，Shijiazhuang Flight College of Air Force，Shijiazhuang 050081，China)

The paper based on the initial design of the swing device in a coaxial rotary measurement system,and the result of the modal analysis on the swing device shows that the first-order mode frequency of the swing device was low.In order to avoid the resonance between the swing device and the excitation frequency of detection field,and improving the accuracy of detection,we optimized the construction of the swing device by means of sensitivity analysis in the Workbench.In this way we obtained the best design project of the swing device.The research has important implications for improving the accuracy of detection and preventing resonances,and gives well theoretical support for the further design improvements.

revolving body;modal analysis;optimization design;sensitivity analysis

2014-05-28

金印(1990-)，男，辽宁营口人，硕士研究生，主要研究方向：航空发动机试验与先进测试技术，E-mail：522549495@qq.com； 石宏(1961-)，女，辽宁沈阳人，教授，主要研究方向：航空发动机制造与维修，E-mail：shihong0809@163.com。

2095-1248(2014)05-0034-05

TH122

A

10.3969/j.issn.2095-1248.2014.05.007