薄壁板结构随机声激励振动响应计算与分析
2014-08-29张国治沙云东冯飞飞
张国治,沙云东,朱 林,冯飞飞
(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)
薄壁板结构随机声激励振动响应计算与分析
张国治,沙云东,朱 林,冯飞飞
(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)
针对航空发动机压气机转子叶片结构声振动问题,建立了薄壁板有限元简化模型,基于耦合有限元/边界元法对薄壁板在行波加载下随机声激励振动响应进行了仿真计算,得到了在不同声压级下的应力响应结果。改变声载荷激励方向,分别对薄壁板施加单音噪声激励和宽频随机噪声激励,通过仿真计算得到了不同角度随机声激励下薄壁板振动响应频响曲线。对比分析发现,薄壁板模态振型与噪声加载方向是引起薄壁板共振的重要因素。
薄壁板;耦合有限元/边界元法;行波加载;随机声激励;振动响应
压气机转子叶片是航空发动机的关键零部件之一,对发动机的整体性能特别是安全性和可靠性影响重大,转子叶片数量多、工作条件恶劣。而且处于气流场、压力场、声场、温度场等多场耦合的复杂工作环境下,致使其应力水平均较高,容易因振动而产生高循环疲劳,导致裂纹、折断等故障,造成严重事故。因此,研究压气机转子叶片的振动特性对于航空发动机的稳定性有重要意义[1]。
二十世纪50年代,首次发现高强度喷气噪声对飞机结构造成破坏,结构声疲劳破坏问题开始受到研究部门的重视[2]。随后,科研工作者对航空结构声振动问题做了大量的研究。弹性结构振动分析方法可分为解析法、数值法和试验法,其中数值分析方法主要有:有限元法[3-4],边界元法[5],有限元/边界元法[6]和统计能量法。有限元法由于其容易模拟复杂结构数值计算,被广泛应用于仿真计算中,但在无限流场中,有限元法不能将全部流场进行离散,只能进行有限截断,这必然导致一定的误差;边界元法只在求解域边界上进行离散,在域内进行解析,计算简单、适应性强、精度高,但其无法计算结构振动;有限元/边界元法综合有限元法和边界元法的优点,采用有限元法对结构进行离散,利用边界元法对结构外表面进行划分,计算精度高。近些年来,国内外科研工作者主要采用有限元/边界元法对薄壁弹性结构进行研究。陈美霞教授等采用FEM/BEM法对内部声激励下壳体的声辐射问题进行了研究[7],在FEM/BEM法基础上进行改进,提出了一种基于随机激励理论计算结构在湍流激励下振动特性的半解析半数值算法[8],并与相关试验结果进行了对比,确定了其方法的正确性。Chuh Mei 等人采用有限元方法对矩形薄板在声载荷作用下的振动响应和声辐射进行了研究[9],随后采用FEM/BEM法对板在热声载荷下振动响应及声辐射进行了研究[10],对有限单元和边界单元进行了精确化分析,建立了板-腔系统,应用连续单元和线性单元腔体边界进行划分,对不同材料薄板在声载荷作用下的振动特性及声辐射进行了对比分析。航空发动机转子叶片是典型的板壳结构,本文针对转子叶片建立薄壁板结构简化模型,采用耦合的有限元/边界元方法对薄壁板结构在行波加载条件下进行随机声激振响应计算与分析,研究分析在不同方向声激励下薄壁板的振动响应特性。
1 耦合有限元/边界元法基本理论
耦合的有限元/边界元法是工程中计算结构振动最常用的方法,其基本思路是:采用有限元法推导出结构控制方程;采用边界元法将结构外部空间声场进行离散,计算出空间各节点声压和振动速度;在结构表面进行耦合,即结构表面各单元节点声压和振动速度是相等的,通过有限元法计算得出结构在声载荷下的振动响应。
载荷输入与响应输出之间的基本关系式
Y=H(ω)·X
(1)
式中:H是频响矩阵;X、Y是载荷向量和响应向量。
根据振动理论,线性系统对任意载荷X(t)激励的响应Y(t)可写成卷积形式
(2)
对响应的相关矩阵Ry(τ)=E[y(t)·yT(t+τ)]进行傅里叶变换,得到响应的功率谱密度矩阵,经过整理可写成
Sy(ω)=H(-ω)·Sx(ω)·HT(ω)
(3)
对于耦合的结构网格来说,除了结构上直接作用的力或力矩外,还需要作用由声压差产生的载荷,这样在结构动力学方程中,就需要增加声压差载荷,即
(Ks+jωCs-ω2Ms)·{u1}+Lc·{μi1}={Fs}
(4)
Lc·{μi1}为声压作用在结构上的载荷;Lc为(ns×nμ1)耦合矩阵,即
(5)
将式(4)和式(5)合成写成一个耦合方程的形式,可以得到间接边界元的耦合方程[7]
(6)
由耦合方程(6)可以导出结构在声载荷激励下的频响应函数H(ω)。
应变与位移之间的关系
ε=ε0+z0{κ}
(7)
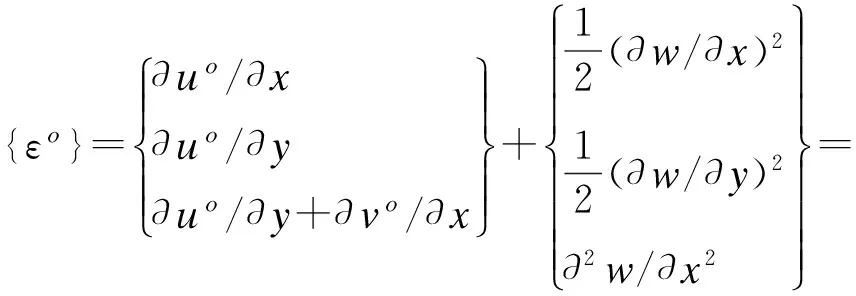
根据应变和应力之间的转化关系,得到应力响应,如式(8)所示
(8)
本文在计算行波加载下薄壁板结构随机声激励振动响应时,采用式(9)作为输入声载荷功率谱密度[11]:
(9)
得出输入声压功率谱密度G(单位:Pa2/Hz),其中:Δf是频带宽度,SPL是输入声压级。将输入功率谱密度Sx(ω)和频响函数H(ω)代入式(3)中,可计算出结构响应的输出功率谱密度Sy(ω)。
2 仿真计算与分析
建立薄壁板有限元模型,采用有限元方法对其进行模态计算,通过边界元方法离散空间声场,计算空间各单元节点声压及振动速度,在结构表面进行结构有限元与声学边界元耦合计算,得出声激励下薄壁板的振动响应结果。以下是具体仿真计算过程。
2.1 薄壁板模态分析
结构的模态频率和振型是结构的主要振动特性,是计算结构动态特性的重要参数,对薄壁板进行模态分析,是研究薄壁板振动特性的一项重要工作。薄壁板结构模型如图1所示,尺寸参数为:长度a=70 mm,宽度b=30 mm,厚度为t=2 mm。建立有限元模型,如图2所示,结构材料:密度ρ=4 370 kg/m3,弹性模量E=113 GPa,泊松比ν=0.3,阻尼系数η=0.01。流体密度ρ=1.225 kg/m3,声速c=340 m/s。对薄壁板进行了模态计算,得出前四阶模态振型及固有频率,如图3所示。

图1 薄壁板结构
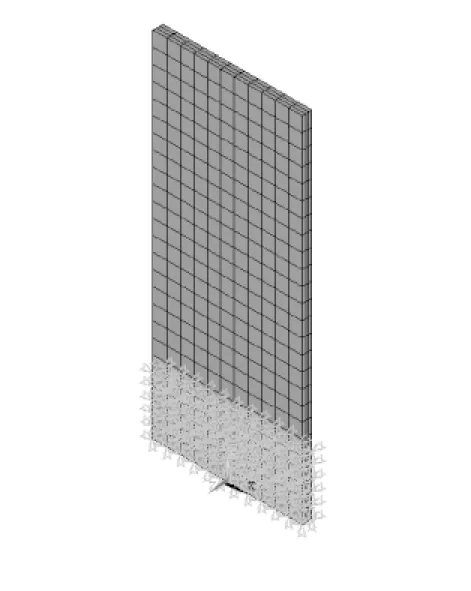
图2 薄壁板有限元模型
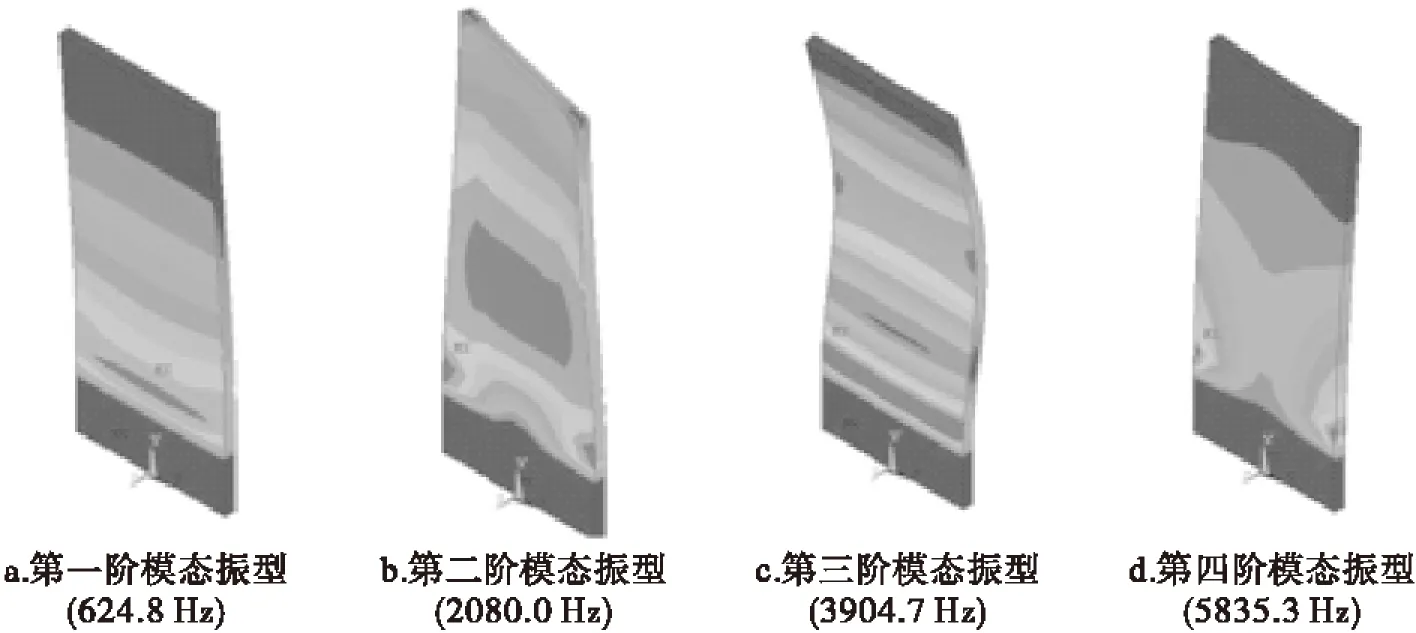
图3 薄壁板前四阶模态振型及频率(Von Mises应力)
2.2 薄壁板行波加载方式
本文选择从四个方向分别对薄壁板进行声激励,而后采用两种旋转方式进行声激励,即垂直方向(0~90°)和水平方向(0~360°),行波加载方式如图4所示。
2.3 薄壁板在随机声激励下的响应计算
发动机是典型的旋转机械,因此发动机内部周期性旋转的叶轮机与气流(燃气)周期性干涉会产生典型的单音噪声;此外,空气和燃气在发动机内部流动过程中,由于粘性的作用和强烈燃烧过程的作用等,在发动机内部气流表现为强烈的湍流脉动,因此发动机的噪声中也包含较强的宽频随机噪声[12]。因此,本文对薄壁板结构进行了单音噪声加载和宽频随机噪声加载,得到在不同声压级下薄壁板振动响应结果(Von Mises 应力功率谱密度)。
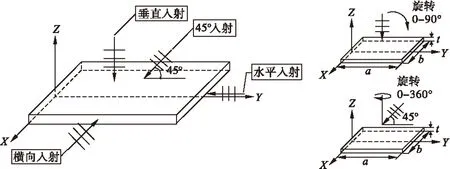
图4 行波加载方式
(1)单音噪声激励
分别在垂直方向、45°方向、水平方向和横向四个方向上对薄壁板进行单音噪声激励。声压级范围为120~160 dB,间隔分别取10 dB和3 dB进行研究,其中:120~160 dB以10 dB为间隔,140~161 dB以3 dB为间隔,频响曲线如图5~6所示。
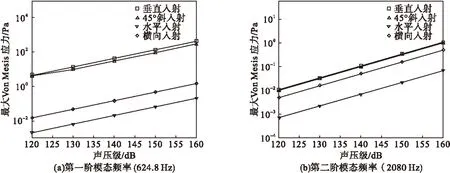
图5 薄壁板在不同方向声激励下Von Mises应力(声压级范围120~160 dB)
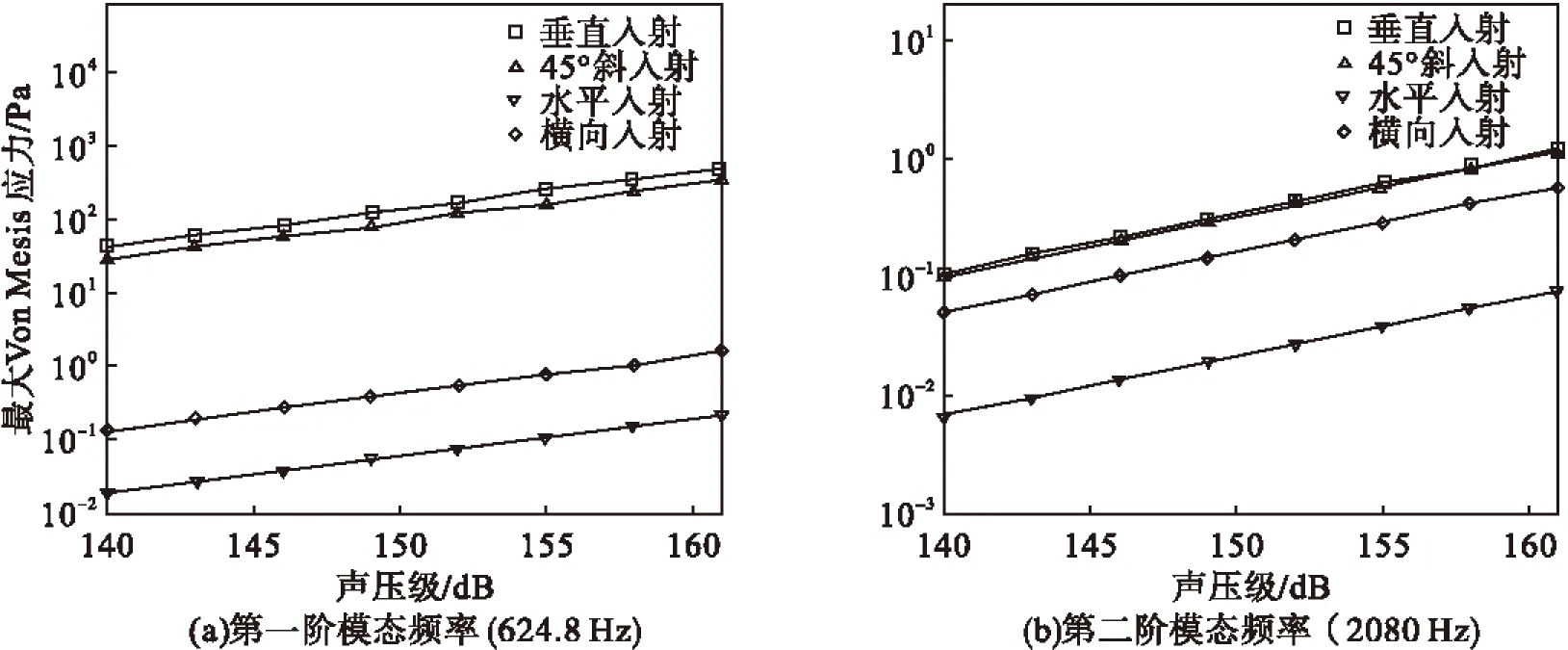
图6 薄壁板在不同方向声激励下Von Mises应力(声压级范围140~161 dB)
薄壁板在四个方向声激励下,垂直方向噪声激励薄壁板的应力响应最明显:第一阶模态频率处,弯曲振型的薄壁板在四个方向声激励下的振动响应相差巨大,可忽略水平方向的噪声激励;第二阶模态频率处,扭转振型的薄壁板在四个方向声激励下的振动响应相仿。
以两种旋转方式对薄壁板进行了行波加载,即垂直0~90°旋转和水平0~360°周向旋转。根据模态振型,在最大应力点位置安装传感器,测点位置如图7所示。
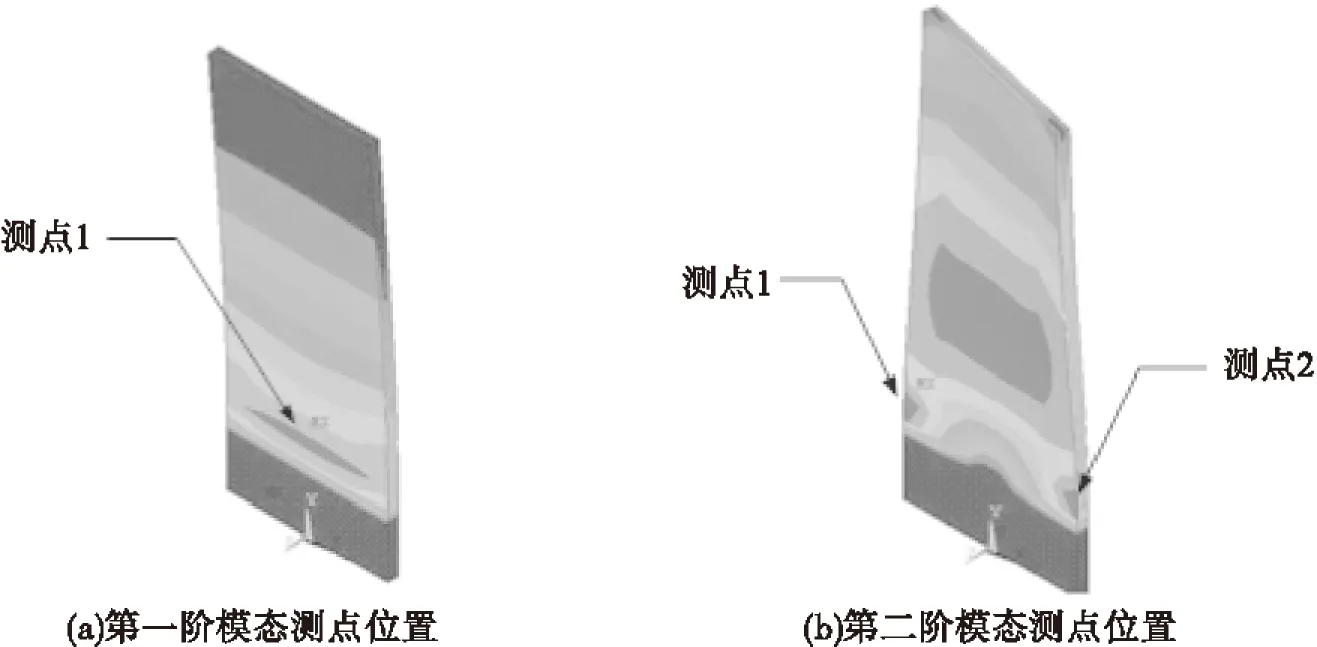
图7 薄壁板Von Mises应力传感器测量位置
改变声载荷入射方向,通过仿真计算得到不同方向声激励下薄壁板Von Mises应力测量结果,如图8所示。
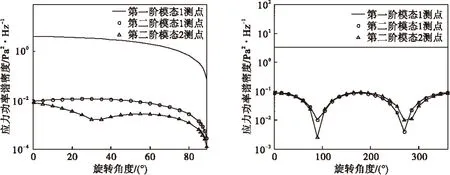
图8 旋转声激励下薄壁板Von Mises应力响应测量结果
声载荷入射方向在垂直方向旋转,第一阶模态(一弯)和第二阶模态(一扭)响应曲线基本一致,呈现良好的线性关系,符合余弦分布规律,如图9所示;声载荷入射方向在水平方向旋转,第一阶模态频率处应力响应不随声载荷入射角度的变化而改变,第二阶模态频率处应力响应有明显的变化,与薄壁板扭转振型一致,呈现周期性变化。
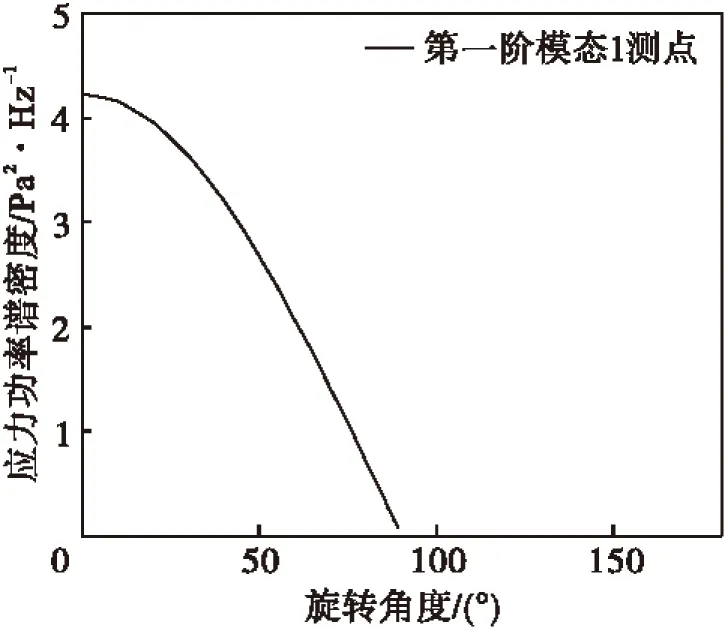
图9 垂直方向声激励下薄壁板第一阶模态频率处Von Mises应力响应测量结果
(2)宽频随机噪声激励
在声压级为150 dB条件下,分别在选中的四个方向上对薄壁板进行了宽频随机声载荷激励(16~6 000 Hz),得到Von Mises应力频响曲线如图10所示。
对薄壁板在不同方向进行宽频随机噪声激励,从频率响应曲线可以看出:在各阶模态频率处,有明显的应力响应共振峰值出现,但在不同方向声激励下的共振峰值位置有所改变。通过对比分析发现:从入射方向观察,薄壁板模态振型对称,则在该模态频率位置有响应共振峰值出现。这与George Tzong[13]的模态分析结论一致。
3 结 论
本文采用耦合有限元/边界元法对行波加载下薄壁板随机声激励振动响应进行了仿真计算,着重分析在不同方向行波加载条件下薄壁板的振动特性,分析结果如下:
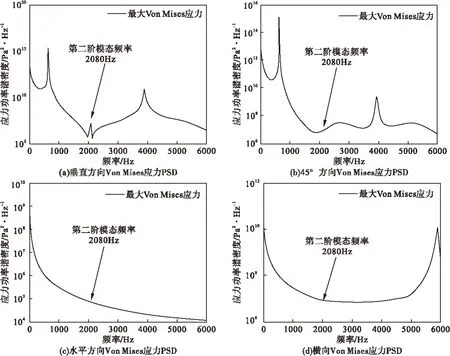
图10 薄壁板在宽频随机噪声激励下Von Mises应力PSD(1~6 000 Hz,150 dB)
(1)基于耦合有限元/边界元法,得到了薄壁板结构在不同方向声载荷激励下振动响应计算结果,声载荷在结构表面垂直方向分量越大,受激励面积越大,结构振动响应越明显。
(2)在相同行波加载条件下,薄壁板不同固有模态振型对其振动响应影响不同:弯曲振型的薄壁板应力集中,相对扭转振型振动响应明显;扭转振型的薄壁板,相对形变较大,则弯曲振型振动响应相对稳定。
(3)对薄壁板进行随机噪声激励,发现薄壁板固有模态振型与噪声加载方向是引起薄壁板共振的重要因素:从噪声入射方向观察,薄壁板模态振型对称,则出现应力响应峰值。
[1]林左鸣,李克安,杨胜群.航空发动机压气机转子叶片声激振试验研究[J].动力学与控制学报,2010,8(1):7-12.
[2]Curlett BP,Gould L J.Flexible Method f or Inter-Object Communication in C++[P].NASA-TM-106315,Nov.,1994.
[3]Smith R R,Hunt J T,Barach D.Finite element analysis of acoustically radiation structures with application of sonar transducers[J].Journal of the Acoustical Society of America,1974,55:1277-1288.
[4]Craggs A.The use of simple three-dimensional acoustic finite element for determining the natural modes and frequencies of complex shaped enclosure[J].Journal of Sound and Vibration,1972,23:331-339.
[5]郑建军,刘兴业,周新竹.边界元法及其在结构分析中的应用[M].合肥:安徽科技出版社,2006:1-227.
[6]Pates C S.Analysis of Random Structure-Acoustic Interaction Problems Using Coupled Boundary Element and Finite Element Methods[D].Norfolk in Virginia of U.S.A:Old Dominion University,1994.
[7]陈美霞,邱昌林,骆东平,等.基于FEM /BEM法的内部声激励水下圆柱壳声辐射计算[J].中国舰船研究,2007,2(6):50-54.
[8]陈美霞,魏建辉,乔志,等.湍流激励下结构振动特性的半解析半数值算法研究[J].振动工程学报,2011,24(6):689-695.
[9]Chuh Mei.Large-amplitude multimode response of clamped rectangular[J].AIAA.1983-1033.
[10]Carl S.Pates,Chuh Mei,Uday Shirahatti,et al.Coupled Boundary/Finite Element Methods for Random Structural-Acoustic Interaction Problems[J].AIAA,1995-1346.
[11]沙云东,闻邦椿,屈伸,等.薄壁结构在随机噪声载荷作用下的动态响应[J].东北大学学报,2005(S1):83-86.
[12]乔渭阳.航空发动机气动声学[M].北京:北京航空航天大学出版社,2010:1-113.
[13]George Tzong.Verification studies on hypersonic structure thermal/acoustic response and life prediction methods[J].AIAA,2013:1664.
(责任编辑:刘划 英文审校:刘红江)
Calculationandanalysisonvibrationresponseofthin-panelsunderrandomacousticload
ZHANG Guo-zhi,SHA Yun-dong,ZHU Lin,FENG Fei-fei
(Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136)
To solve the structure-acoustic problems of the compressor rotor blades of aircraft engines,a simplified finite element model of thin-panel structure is created.Based on the FEM/BEM,the simulation of the thin-panel structure for traveling wave loading is taken under random acoustic excitation to obtain the stress response results of the structure at different sound pressure levels.The tone acoustic excitation and broadband random acoustic excitation in various directions are applied on thin panels.Through simulation,the vibration frequency response curves are obtained.The comparative analysis shows that the model shape and acoustic loading direction are the key factors of the thin-panel structure resonance.
thin-panel;FEM/BEM;propagation wave loading;random acoustic excitation;vibration response
2013-10-15
张国治(1986-),男,吉林柳河人,在读研究生,主要研究方向:航空发动机强度振动及噪声,E-mail:zhangguozhi617@163.com;沙云东(1966-),男,黑龙江阿城人,教授,主要研究方向:航空发动机强度、振动及噪声,E-mail:ydsha2003@vip.sina.com。
2095-1248(2014)04-0023-06
V214.4
A
10.3969/j.issn.2095-1248.2014.04.005
