基于Kriging模型的离心叶轮结构优化设计
2014-08-29赖喜涛温卫东冯大俊
赖喜涛,温卫东,冯大俊
(1.江苏省航空动力系统重点实验室,南京 210016; 2.机械结构力学及控制国家重点实验室,南京 210016;3.南京航空航天大学 能源与动力学院,南京 210016; 4.中国人民解放军94994部队,南京 210017)
基于Kriging模型的离心叶轮结构优化设计
赖喜涛1,2,3,4,温卫东1,冯大俊2
(1.江苏省航空动力系统重点实验室,南京 210016; 2.机械结构力学及控制国家重点实验室,南京 210016;3.南京航空航天大学 能源与动力学院,南京 210016; 4.中国人民解放军94994部队,南京 210017)
研究了以减重为目标的航空发动机离心叶轮结构优化问题,将Kriging模型与遗传算法相结合,应用拉丁方试验设计和有限元分析生成初始样本数据,利用初始样本数据建立离心叶轮重量和最大应力等状态参数的Kriging模型,运用遗传算法对该Kriging模型在设计空间进行全局寻优,利用有限元分析方法计算近似最优设计点的状态参数,并以此更新已有的设计样本数据,不断提高 Kriging 模型的近似精度。计算结果表明,基于Kriging模型-遗传算法的离心叶轮结构优化设计方法不仅可以获得良好的优化结果,比直接用遗传算法寻优减少了大量计算时间,提高了设计效率,同多项式模型-遗传算法相比也有效率优势。
离心叶轮;结构优化;Kriging模型;遗传算法
在航空发动机离心压气机中离心叶轮是重要的核心部件,由于其工作转速高,对其强度的要求很高。一般在流场计算、强度有限元分析后,需要对叶轮进行结构优化,以减轻结构重量或减小应力幅值。张明辉[1]运用改进的遗传算法对离心叶轮进行减重的结构优化;雒婧[2]对离心叶轮外轮廓型线进行了减应力的结构优化;蔡显新等[3]对整体离心叶轮进行了延寿减重的多学科形状优化设计。
随着离心叶轮性能的进一步提高,有限元分析时还需要考虑温度载荷,以更接近工程实际。而考虑温度载荷后的热-固强度耦合计算分析,并进行结构优化设计,需要进行大量有限元分析计算。如果直接运用优化算法进行搜索寻优必然耗时巨大,优化效率低。因此目前在结构优化中多采用代理模型对复杂有限元分析模型进行近似,以减小计算量,提高优化效率。优化算法多采用遗传算法,以得到全局最优解。常用的代理模型技术主要有多项式模型、人工神经网络模型、Kriging模型、径向基函数模型等[4]。
目前对离心叶轮进行热-固耦合强度有限元分析,并进行代理模型-遗传算法结构优化的文献较少。刘涛[5]在组合压气机转子结构优化中对离心叶轮进行了热-固耦合强度计算,并对轮毂、辐板等处运用多项式模型-遗传算法进行了减重的结构尺寸优化。多项式模型简单易用,极易实现寻优,但需要的样本点较多,局部拟合精度差,适合于处理非线性程度较低且精度要求不高的问题。而Kriging模型需要的样本点较少,全局和局部拟合精度都很高,目前已广泛运用于工程领域[6-9]。本文运用Kriging模型-遗传算法对考虑温度载荷作用下的某离心叶轮进行减重结构优化,并与多项式模型-遗传算法优化方法和直接用遗传算法搜索优化方法进行对比,验证了Kriging模型-遗传算法优化方法的优越性。
1 Kriging代理模型
代理模型的本质是指计算量小但其计算结果与高精度复杂模型的计算结果接近的分析模型。代理模型是一种包含试验设计和近似算法的建模技术,在设计优化过程中用代理模型替代原有的高精度分析模型,可以提高仿真优化的寻优效率,降低算法的计算成本。
Kriging模型是由南非地质学者Danie Krige于1951年提出的一种估计方差最小的无偏估计模型,原是用来估算矿藏的储量分布。该模型比单个的参数化模型更具有灵活性,同时又克服了非参数化模型处理高维数据存在的局限性[10]。
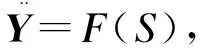
F(X)=G(X)+Z(X)
(1)
式中:X为n维输入设计参数的集合;F(X)为q维响应参数的集合。
G(X)为一个p阶线性多项式f(x)的回归模型,即:
G(X)=f(X)Tβ
(2)
式中:β是回归模型的权系数。
本文提出了一种基于单步统计特征进行速度识别方法。此方法首先利用固定在脚部的IMU获取人员在跑步机上以1.5 m/s~4 m/s的不同的速度运动的惯性传感数据,其次采用峰值检测的方法对采集到的大量惯性传感数据进行单步数据单元划分,然后从每个单步数据单元中提取指定的65维统计特征,最后采用机器学习分类算法对每种速度的特征进行学习,使用训练获得的模型识别不同的单步惯性传感数据所对应的速度。
Z(X)代表一个随机过程。
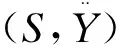
F(X)=f(X)Tβ*+R(X)TY*
(3)
详细过程见文献[10]。
2 优化方法
在优化中,运用Kriging代理模型-遗传优化方法时,初始样本点由试验设计方法(Design of Experiments,DOE)生成。常用试验设计方法有中心复合设计、均匀设计、拉丁方设计和正交设计等。本文选用应用较广泛的拉丁方设计的方法。拉丁方试验设计是一种基于随机抽样的试验设计方法,具有均衡分散性和整齐可比性等特点,适用于多因素、采样空间大的研究[11]。Kriging代理模型-遗传优化流程如图1所示。具体优化计算时,运用UG软件和ANSYS Workbench软件。
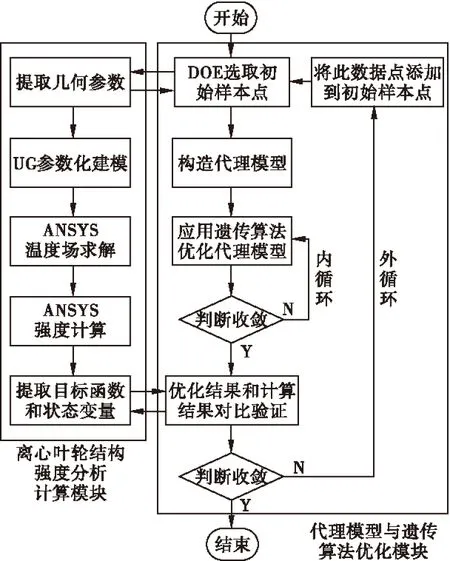
图1 离心叶轮结构强度优化计算流程图
(1)通过拉丁方设计方法生成初始样本点,并在离心叶轮强度分析计算模块中计算这些样本点,得到初始数据点。
(2)由初始数据点构造Kriging代理模型。
(3)将代理模型式(3),转化为遗传算法的适应度函数,经过编码、解码、交叉、变异等寻优搜索后,种群进化,得到代理模型的预测最优解。
将代理模型的预测最优解f1与该处的叶轮强度数值计算真实结果f2对比,如满足收敛条件,则优化完成;如不满足收敛条件,则将此次数值计算得到的真实数据点添加到初始数据点中,转步骤(2),重新构造代理模型,再次应用遗传算法对更新后的代理模型进行优化,直至收敛,完成优化。
3 算例分析
某离心叶轮内径20 mm,外径143 mm,叶片为15个,在UG软件中建立其1/15模型如图2所示。叶轮所用材料为钛合金TC11,工作温度盘心为50 ℃,叶片上表面为180 ℃;转速40 000 RPM;轮盘支板右端面受97 500 N轴向力;叶轮轮缘左端面周向和轴向约束。强度以EGD-3应力标准[12]进行校核,即:最大离心径向应力不大于屈服强度的80%;盘内径上的周向应力不大于屈服强度的95%;等效应力不大于屈服强度。
TC11材料属性[13]为:密度ρ=4.48 g/cm3,20 ℃~200 ℃线膨胀系数α=9.3×10-6/℃,泊松比μ=0.33,不同温度下的导热系数λ、弹性模量E、屈服强度σ0.2和极限强度σb见表1、表2、表3所示(强度为TC11饼坯的强度值)。
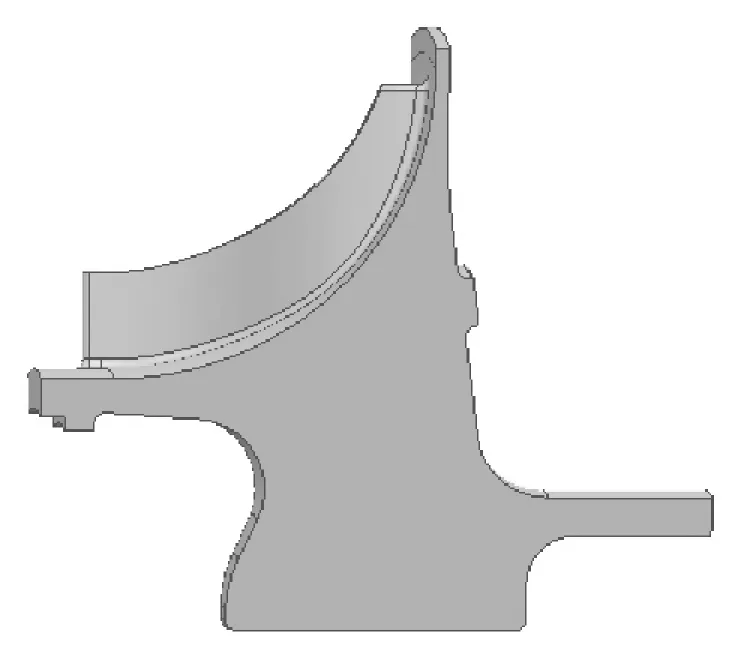
图2 离心叶轮1/15模型

表1 钛合金TC11不同温度下的材料参数
将所建模型导入ANSYS Workbench,单元选择10节点四面体结构单元solid187,进行热-固静力学分析。计算可知:最大等效应力σmax发生在盘心处,值为735.98 MPa,该处温度为50 ℃,则该处屈服强度为932 MPa,安全系数为1.27。最大周向应力σθ max发生在盘心处,温度为50 ℃,值为704.49 MPa,则该处许用周向应力为0.95σ0.2=885.4 MPa,安全系数为1.26。最大径向应力σr max发生在叶根前缘处,值为632.04 MPa,该处温度为117 ℃,则该处许用径向应力为0.8σ0.2=676.8 MPa,安全系数为1.07。
3.1 定义优化设计参数
在不影响流道面、不改变与相邻部件连接部位、不改变中心拉杆与轮盘接触面的前提下,离心轮盘可优化部位如图3所示,有A、B两处(粗实线部分)。本算例选择A处进行优化,将A处(直线+圆弧)以4点控制、中间2点自由的3阶样条曲线代替,以这2个自由点的4个自由度为优化设计参数,如图4所示,设计参数初值、范围及优化后终值见表2。
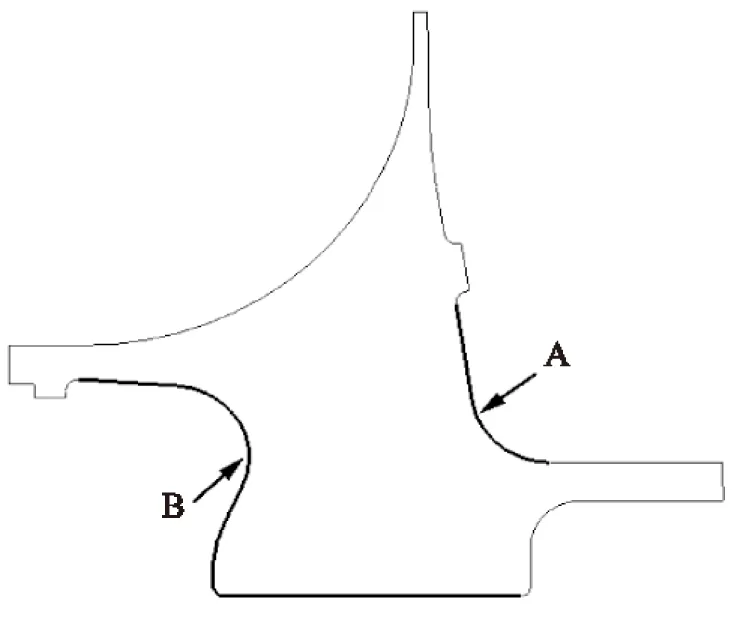
图3 离心轮盘结构优化部位
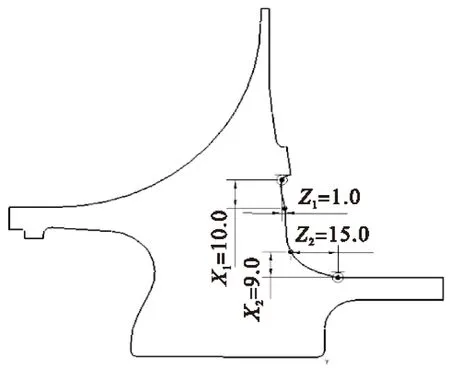
图4 轮盘优化设计参数
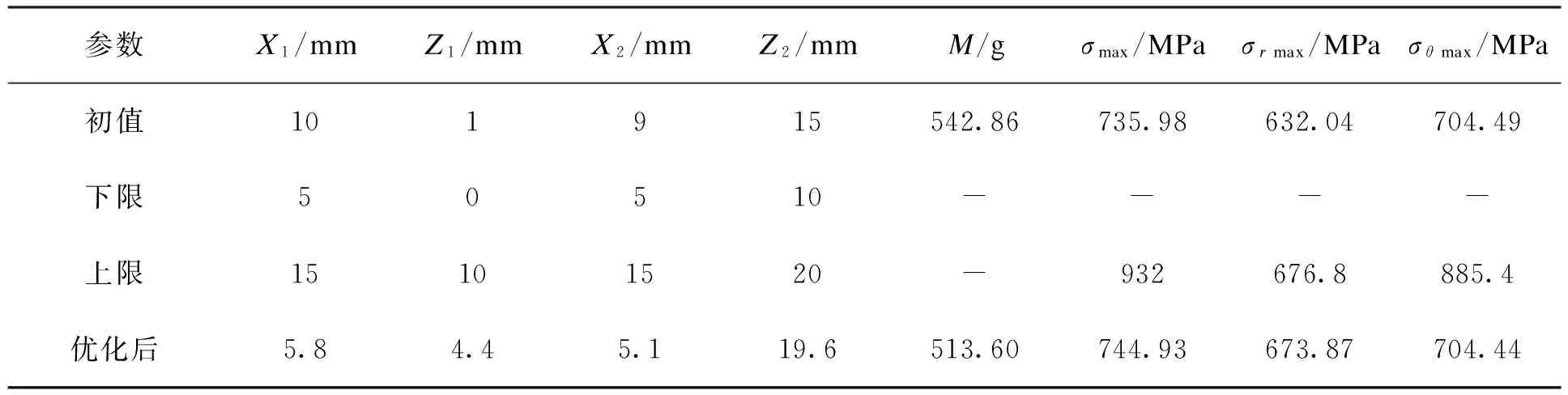
表2 优化设计参数初值、范围及优化后终值
3.2 优化分析计算
该离心叶轮结构优化模型如下:
目标函数:minf(x)=M;
设计参数:X={X1,Z1,X2,Z2}T;
约束条件:σmax≤932 MPa;σθ max≤885.4 MPa;σr max≤676.8 MPa;5≤X1≤15;0≤Z1≤10;9≤X2≤15;10≤Z2≤20.
其中M是为离心叶轮的质量。
按图1所示流程进行优化分析计算。选择拉丁方设计,生成15个初始样本点并计算,得到表3。从表3中可以看出,拉丁方设计产生的样本点每个因素的水平只采用一次,较好地填充了设计空间,使样本点更具代表性。定义ε=1%,经过4次外循环迭代,得到最优解。优化结果见表2。最终模型预测值与真实计算值的相对误差如表4所示,可见Kriging代理模型的精度较高。
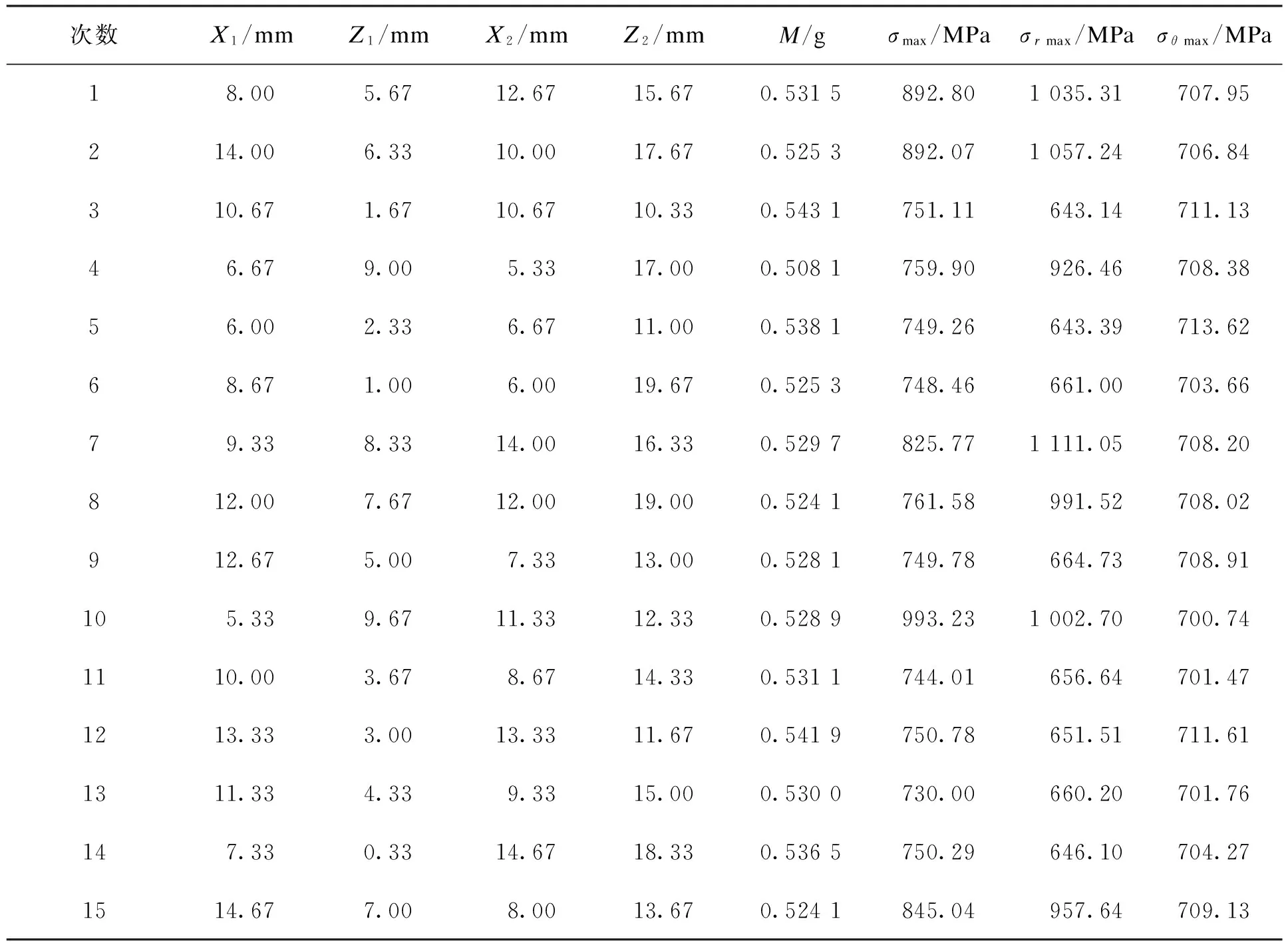
表3 初始样本点数据
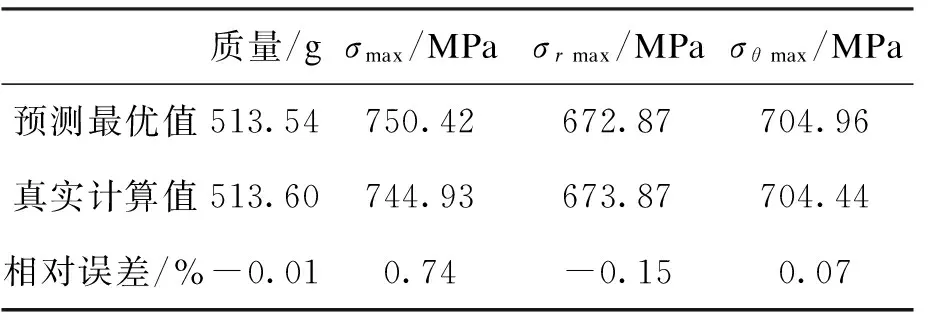
表4 预测最优值与真实计算值相对误差
优化前后离心叶轮截面对比和等效应力分布对比分别如图5、图6所示。图5中虚线为优化后截面,实线为优化前截面。从图5可以看出优化效果较明显。
从表2可知,优化后质量减少5.39%,最大等效应力值和最大径向应力值略有增加,但都还满足强度校核准则要求,材料利用率得到提高。后续设计时可以再对图3中B处曲线进行优化。
在优化分析过程中,所用计算机配置为Intel(R)Core(TM)i7-3770k @3.50 GHz、内存16 G。
运用Kriging代理模型-遗传算法寻优,样本点加外循环迭代,共进行27次有限元分析,总耗时约30 min;运用多项式模型-遗传算法寻优,共进行31次有限元分析,总耗时约35 min;而直接用遗传算法寻优,共进行305次有限元分析,总耗时约330 min。
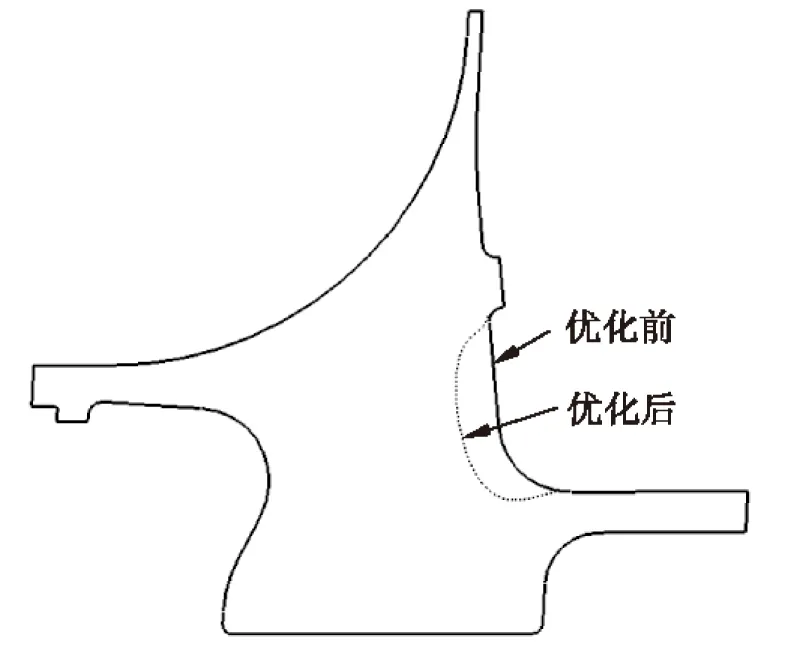
图5 离心叶轮结构优化前后截面对比

图6 叶轮等效应力分布
4 结 论
基于Kriging代理模型的离心叶轮结构优化设计,在保证一定精度的前提下极大地减少了计算量,提高了优化效率,缩短了设计周期。Kriging模型-遗传算法与多项式模型-遗传算法相比,所需时间更少,效率更高。因此Kriging模型-遗传算法的运用具有重要的工程应用价值。
[1]张明辉,王尚锦.改进的遗传算法用于离心叶轮优化设计[J].西安交通大学学报,2001,35(9):914-917.
[2]雒婧,席光,郭常青.离心叶轮的应力数值分析与结构优化[J].流体机械,2004,11(32):8-10.
[3]蔡显新,熊纯,周康丽.航空发动机离心叶轮的多学科设计优化[J].长沙航空职业技术学院学报,2008,8(4):23-26.
[4]穆雪峰,姚卫星,余雄庆,等.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608-612.
[5]刘涛.组合压气机转子结构强度优化分析[D].南京:南京航空航天大学,2013.
[6]谢素超,周辉.基于Kriging法的铁道车辆客室结构优化[J].中南大学学报(自然科学版),2012,43(5):1990-1998.
[7]宋磊,王建,杨卓懿.Kriging模型在潜器型线优化设计中的应用研究[J].船舶力学,2013,17(1-2):8-13.
[8]何欢,朱广荣,何成,等.基于Kriging模型的结构耐撞性优化[J].南京航空航天大学学报,2014,46(2):297-303.
[9]李小刚,程锦,刘振宇,等.基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J].机械工程学报,2014,50(3):165-174.
[10]肖立峰,张广泉,张以都.基于Kriging代理模型的结构形状优化方法[J].机械设计,2009,26(7):57-60.
[11]王国春,成艾国,胡成辉,等.基于Kriging模型的汽车前部结构的耐撞性优化[J].汽车工程,2011,33(3):208-212.
[12]罗尔斯·罗伊斯公司.EGD-3 Spey MK202发动机应力标准[M].丁爱祥,吴君,译.北京:国际航空编辑部,1979:6-9.
[13]师昌绪.中国航空材料手册[M].第二版第四卷,钛合金、铜合金.北京:中国标准出版社,2002:147-172.
(责任编辑:刘划 英文审校:刘红江)
StructuraloptimizationofacentrifugalimpellerbasedonaKrigingmodel
LAI Xi-tao1,2,3,4,WEN Wei-dong1,FENG Da-jun2
(1.Jiangsu Key Laboratory of Aerospace Power Systems,Nanjing 210016; 2.State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing 210016; 3.Nanjing University of Aeronautics and Astronautics,Nanjing 210016; 4.Unit 94994 of PLA,Nanjing 210017)
Based on a Kriging model and genetic algorithm,the structural optimization of a centrifugal impeller is studied in order to reduce the weight of an airplane.Obtained from Latin square experimental design and finite element analysis,the initial data is used to establish a Kriging parameters model of the weight and the maximum stress of the centrifugal impeller,which is then global optimized by genetic algorithm.The state parameters of the approximate optimum point are calculated with finite element analysis in order to update the existing sample data and to improve the approximate accuracy of the model.The results show that compared with direct searching with genetic algorithm,the combination of a Kriging model and genetic algorithm can get a good optimization result and reduce the computing time significantly.This method also has an efficiency advantage over the polynomial model and genetic algorithm.
centrifugal impeller;structural optimization;Kriging model;genetic algorithm
2014-03-05
赖喜涛(1982-),男,重庆巴南人,工程师,主要研究方向:机械结构优化设计,E-mail:autherlake@163.com;温卫东(1958-),男,福建闽清人,教授,博士,主要研究方向:先进复合材料结构与损伤失效、寿命等,E-mail:gswwd@nuaa.edu.cn。
2095-1248(2014)04-0017-06
V211
A
10.3969/j.issn.2095-1248.2014.04.004
