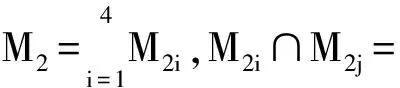4类图完美匹配数目的嵌套递推求法

唐保祥， 任 韩

(1.天水师范学院数学与统计学院，天水 741001;2.华东师范大学数学系，上海 200062)

完美匹配的计数理论在晶体物理学、分子化学和计算机科学中都有重要的应用[1-7],与其他理论课题发生密切联系,产生出许多含义丰富而深刻的理论成果[8-13].

定义1 如果图G的2个完美匹配M1和M2中有一条边不同，那么M1和M2就称为G的2个不同的完美匹配.

定义2 如果G的2个Hamilton圈C1和C2中有一条边不同,那么C1和C2就称为图G的2个不同Hamilton圈.

下面给出本文的结果及其证明.

定理1 3n个长为4的圈为Ci1:ui1ui2ui3ui4ui1,Ci2:vi1vi2vi3vi4vi1,Ci3:wi1wi2wi3wi4wi1(i=1,2,…,n).连接圈Ci1,Ci2,Ci3的顶点ui1与vi1,ui3与wi1,vi3与wi3;再连接Ci1,Ci2,Ci3与Ci+1,1,Ci+1,2,Ci+1,3的顶点ui2与ui+1,4,vi2与vi+1,4,wi2与wi+1,4(i=1,2,…,n-1).把得到的图用3-n3LC4表示(图1).f(n)表示图1的完美匹配的数目,则

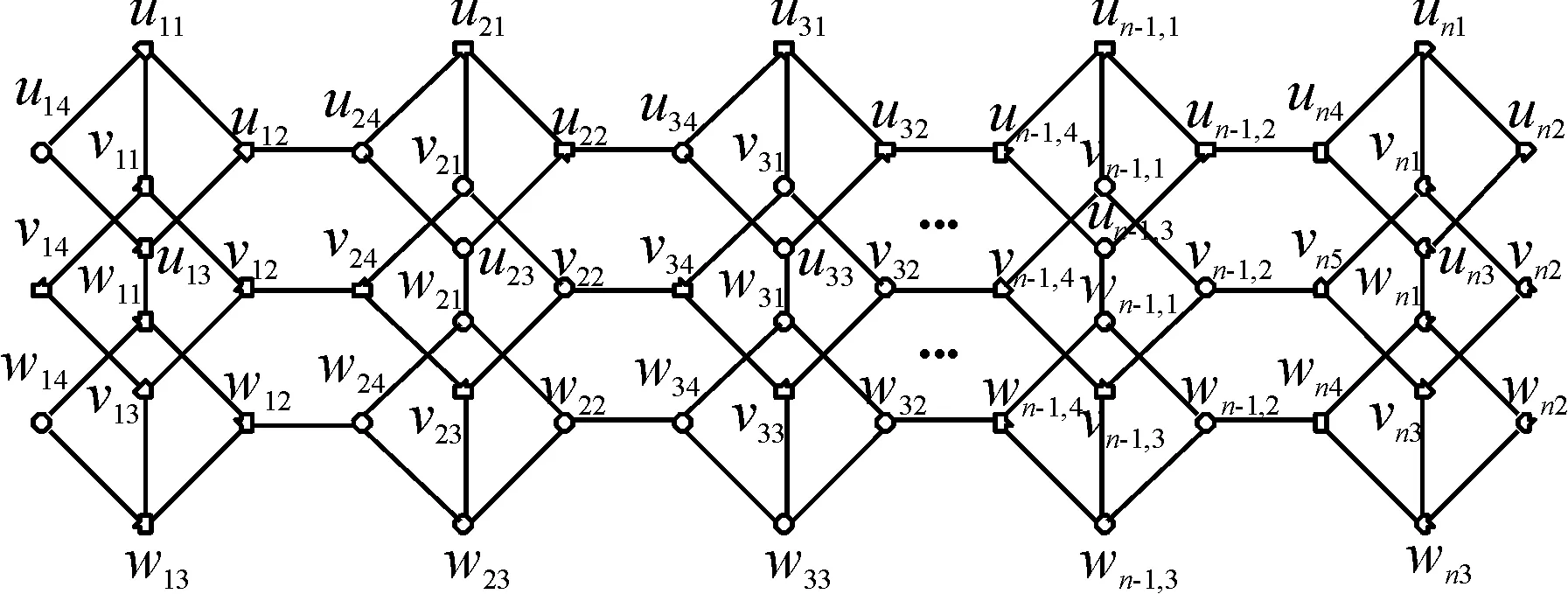
图1 3-n3LC4图Figure 1 Figure of 3-n3LC4

证明为了得到f(n),在此定义3个图G1,G2和G3,且求这3个图完美匹配的数目.将长为3的3条路v1v2w2w1,u2u1v1v2,u1u2w1w2的端点v1和w1,u2和v2,u1和w2分别与图1的顶点v14和w14,u14和v14,u14和w14各连接一条边，得到的图分别用G1、G2和G3表示,如图2～图4.显然图G1、G2和G3都存在完美匹配.α(n)、β(n)和γ(n)分别表示图G1、G2和G3的完美匹配的数目.因G1≅G2,故α(n)=β(n).

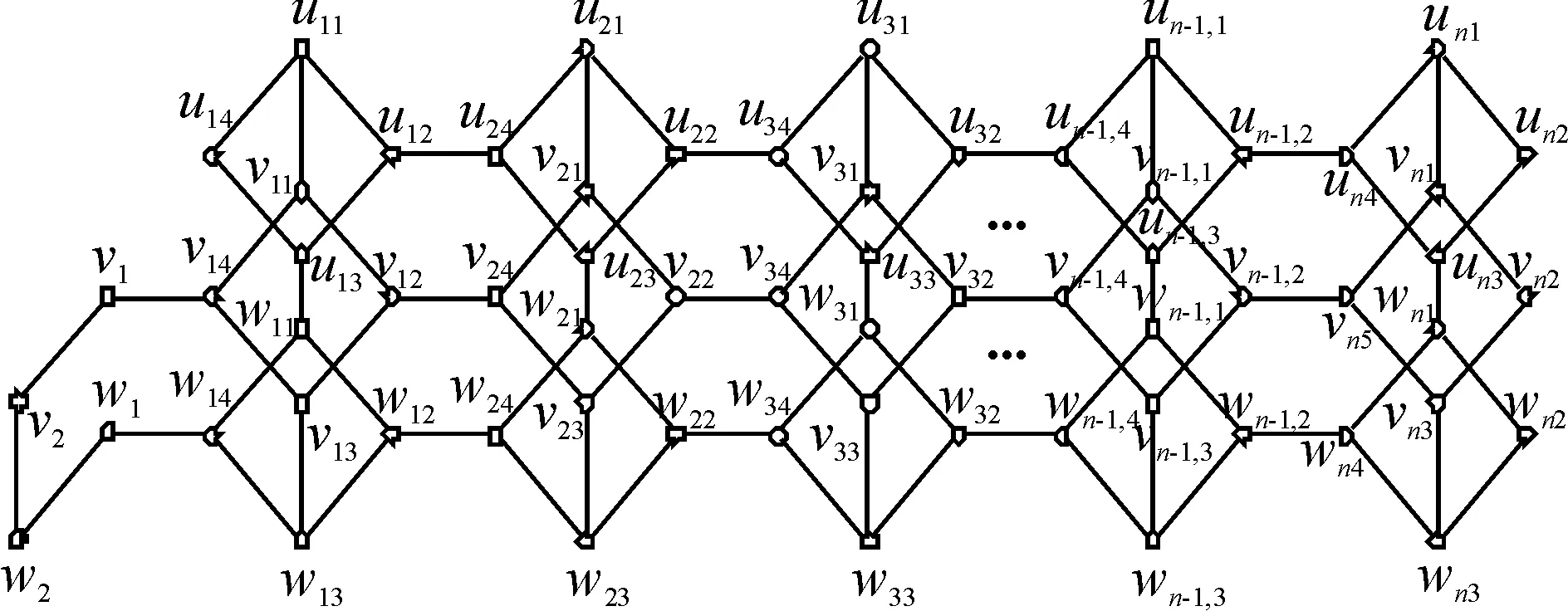
图2 图G1Figure 2 Figure of G1

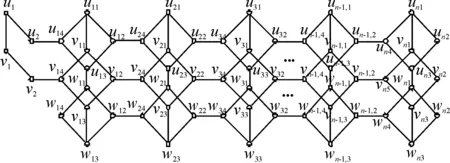
图3 图G2Figure 3 Figure of G2

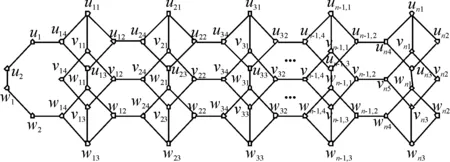
图4 图G3Figure 4 Figure of G3

求α(n).记图2的完美匹配的集合为M,记G1含边v2v1,v2w2的完美匹配集合分别为M1,M2.则Mi≠(i=1,2);M1∩M2=.所以M=M1∪M2,α(n)=|M|=|M1| + |M2|.

求|M2|.

显然M2=M21∪M22,M21∩M22=.故|M2|=α(n-1)+γ(n-1).

综上所述

α(n)=f(n)+α(n-1)+γ(n-1).

(1)

求γ(n).记图4的完美匹配的集合为M,G3含边u2u1,u2w1的完美匹配集合分别为M1,M2.则Mi≠,i=1,2;M1∩M2=. 所以M=M1∪M2,γ(n)=|M|=|M1| + |M2|.

求|M2|.

显然M2=M21∪M22,M21∩M22=.故

|M2|=α(n-1)+β(n-1)=2α(n-1).

综上所述

γ(n)=f(n)+2α(n-1).

(2)

求f(n).显然图1存在完美匹配.记图1的完美匹配集合为M,图1含边u14u11,u14u13的完美匹配集合分别为M1,M2.则Mi⊆M, Mi≠(i=1,2),M1∩M2=.故M=M1∪M2,f(n)=|M|=|M1|+|M2|.

求|M1|.

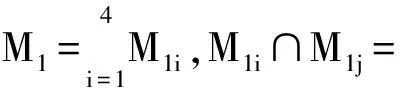
|M1|=f(n-1)+α(n-1)+2γ(n-1).

求|M2|.

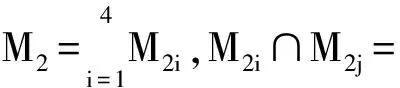
|M2|=f(n-1)+α(n-1)+2β(n-1)=

f(n-1)+3α(n-1).

综上所述

f(n)=2f(n-1)+4α(n-1)+2γ(n-1).

(3)

把式(2)代入式(3),得

f(n)=4f(n-1)+4α(n-1)+4α(n-2).

(4)

由式(1),得

2α(n-1)+2γ(n-1)=2α(n)-2f(n).

(5)

把式(5)代入式(3),得

3f(n)=2f(n-1)+2α(n)+2α(n-1).

(6)

由式(6),得

4α(n-1)+4α(n-2)=6f(n-1)-4f(n-2).

(7)

把式(7)代入式(4),得

f(n)=10f(n-1)-4f(n-2).

(8)

定理2 3n个长为4的圈为Ci1:vi1wi1vi2ui1vi1,Ci2:vi2wi2vi3ui2vi2,Ci3:vi3wi3vi4ui3vi3(i=1,2,…,n),圈Ci1与Ci2具有公共顶点vi2,圈Ci2与Ci3具有公共顶点vi3.连接圈Ci1,Ci2,Ci3的顶点ui1与ui2,ui2与ui3,wi1与wi2,wi2与wi3;再分别连接圈Ci1与Ci+1,1的顶点wi1与ui+1,1,Ci2与Ci+1,2的顶点wi2与ui+1,2,Ci3与Ci+1,3的顶点wi3与ui+1,3.把得到的图用3-nBC4表示(图5).g(n)表示图5的完美匹配的数目,则

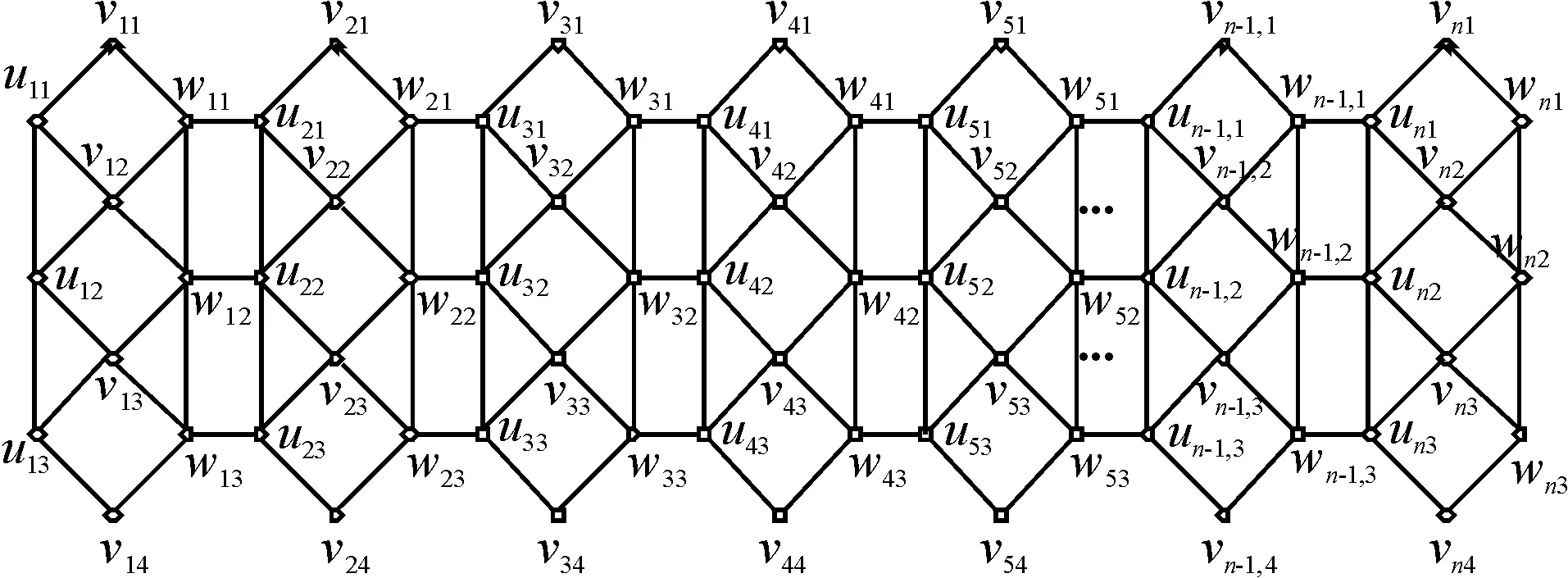
图5 3-nBC4图Figure 5 Figure of 3-nBC4

证明显然图5存在完美匹配.记图5的完美匹配集合为M,图5含边v11u11,v11w11的完美匹配集合分别为M1, M2.则Mi⊆M,Mi≠(i=1,2),M1∩M2=.故M=M1∪M2,g(n)=|M|=|M1| + |M2|.

求|M1|.

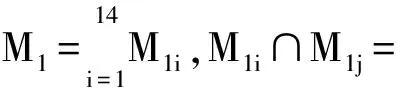
求|M2|.

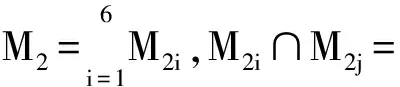
综上所述

g(n)=8g(n-1)+12g(n-2).

(9)

定理3 2n个长为4的圈为Ci1:vi1vi2vi3vi4vi1,Ci2:uivi2vivi4ui,圈Ci1与Ci2具有公共顶点vi2和vi4(i=1,2,…,n).再分别连接圈Ci2与Ci+1,2的顶点ui与ui+1,vi2与vi+1,4,vi与vi+1,ui与vi1,vi与vi3(i=1,2,…,n-1).把得到的图用3-nL4表示(图6).σ(n)表示图5的完美匹配的数目,则

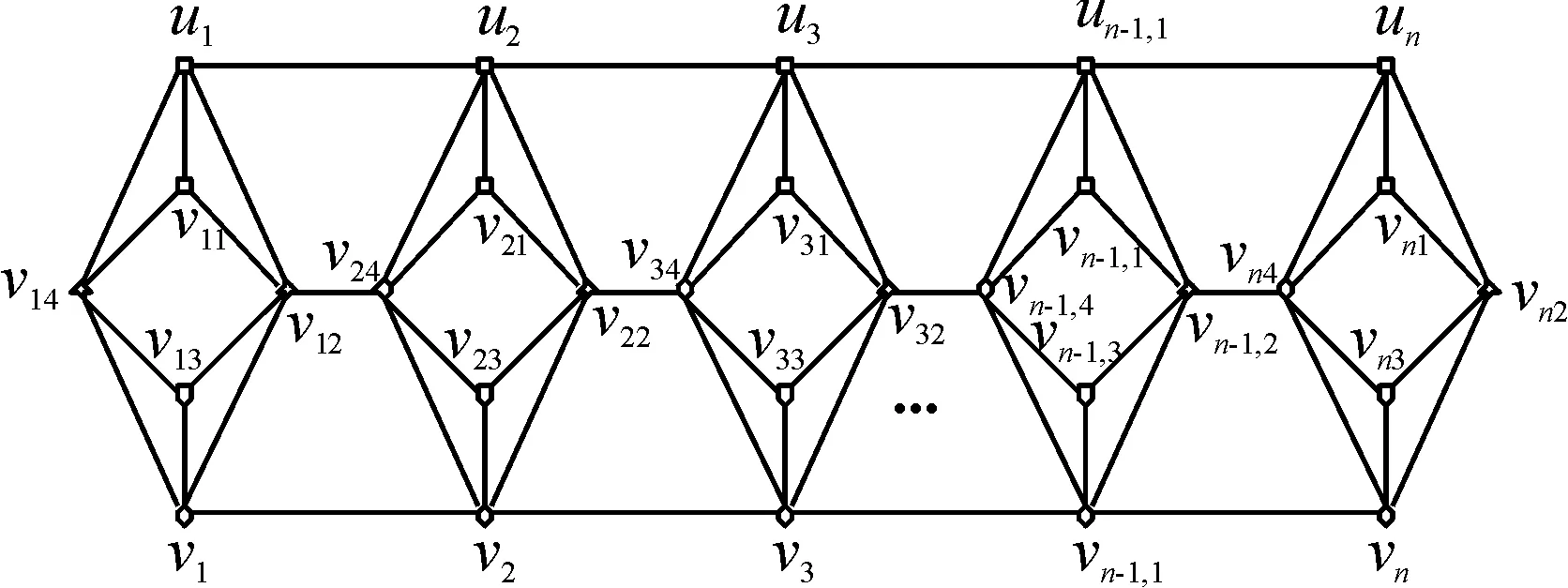
图6 3-nL4图Figure 6 Figure of 3-nL4

证明显然图6存在完美匹配.记图6的完美匹配集合为M,含边v14u1,v14v11,v14v13,v14v1的完美匹配集合分别为M1, M2,M3,M4.则Mi⊆M, Mi≠(i=1,2,3,4),Mi∩Mj=(1≤i

由图6的对称性知|M1|=|M4|,|M2|=|M3|.故σ(n)=2|M1| + 2|M2|.

求|M1|.

求|M2|.

综上所述

σ(n)=4σ(n-1)+6σ(n-2).

(10)

易得σ(1)=4,σ(2)=22.线性递推式(10)的通解为

证毕.

定理4n个长为4的圈为Ci:ui1ui2ui3ui4ui1,连接圈Ci的顶点ui1与ui3(i=1,2,…,n);再连接圈C1与C2的顶点u14与u24;如果i≠n-1,则连接ui2与ui+2,4,否则连接ui2与ui+1,2(i=1,2,…,n-1;n≥2).把得到的图用1-nXC4表示(图7).(n)表示图7的完美匹配的数目,则(n)=2n+1.

图7 1-nXC4图Figure 7 Figure of 1-nXC4

证明显然图7存在完美匹配.记图7的完美匹配集合为M,含边u14u11,u14u24,u14u13的完美匹配集合分别为M1, M2, M3.则Mi⊆M,Mi≠(i=1,2,3),Mi∩Mj=(1≤i

推论1 图7的不同Hamilton圈共有2n个.

证明由定理4的证明过程可知,图7的2n+1个完美匹配中,只有去掉含边u14u24的一个完美匹配中的所有边,才能使图7分裂为n个互不连通的4圈.设M是图7的任一个不含边u14u24的完美匹配,则图7去掉M中所有的边恰得到图7的一个Hamilton圈,且M不同所得到的图7的Hamilton圈也不同,故图7的不同Hamilton圈共有2n个.

参考文献：

[1] Hall G G. A graphic model of a class of molecules[J].International Journal of Mathematical Education in Science and Technology, 1973, 4(3):233-240.

[2] Cyvin S J, Gutman I. Kekulé structures in Benzennoid hydrocarbons[M]. Berlin:Springer Press,1988.

[3] Kasteleyn P W. Graph theory and crystal physics[C]∥Harary F. Graph theory and theoretical physics. London: Academic Press, 1967:43-110.

[4] Ciucu M. Enumeration of perfect matchings in graphs with reflective symmetry[J]. Journal of Combinatorial Theory:Series A,1997,77:87-97.

[5] Fischer I, Little C H C. Even circuits of prescribed clockwise parity[J]. The Electronic Journal of Combinatorics, 2003, 10:1-20.

[6] Jockusch W. Perfect mathings and perfect squares[J]. Journal of Combinatorial Theory:Series A, 1994, 67:100-115.

[7] Kasteleyn P W. Dimmer statistics and phase transition[J]. Journal of Mathematical Physics,1963,4:287-293.

[8] Lovász L, Plummer M. Matching theory[M]. New York:North-Holland Press, 1986.

[9] Yan W G, Zhang F J. Enumeration of perfect matchings of a type of Cartesian products of graphs[J]. Discrete Applied Mathematics, 2006,154:145-157.

[10] 吴钰涵, 尤利华.一类重要的本原(带号)有向图的指数值[J]. 华南师范大学学报:自然科学版, 2011, 43(3):44-48.

Wu Y H,You L H. Indices of an important class of primitive (signed) digraphs[J]. Journal of South China Normal University:Natural Science Edition, 2011, 43(3):44-48.

[11] 唐保祥,任韩. 5类图完美匹配的计数[J]. 中山大学学报:自然科学版, 2012, 51(4):31-37.

Tang B X,Ren H. The number of perfect matchings in five types of graphs[J].Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(4):31-37.

[12] 唐保祥,李刚,任韩. 3类图完美匹配的数目[J]. 浙江大学学报:理学版, 2011, 38(4):16-19.

Tang B X,Ren H.The number of perfect matching for three specific types of graphs[J].Journal of Nanjing Normal University:Natural Science Edition, 2011, 38(4):16-19.

[13] 唐保祥, 任韩.4类图完美匹配的计数[J].武汉大学学报:理学版, 2012, 58(5):441-446.

Tang B X,Ren H. The number of the perfect matchings for four types of graphs[J].Journal of Wuhan University:Natural Science Edition, 2012, 58(5):441-446.