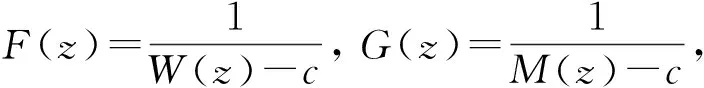涉及重值的代数体函数的唯一性

谭 洋

(中国人民大学信息学院, 北京 100872)

代数体函数是一类多值解析函数, 亚纯函数是代数体函数的特殊情况,如何把亚纯函数的一些重要性质推广到代数体函数是一重要的研究课题. 关于代数体函数的一些基本性质和结果可参阅文献[1]-[4].本文的符号除特别说明外均采用Nevanlinna理论的常用符号[1,5-6].设Ak(z),Ak-1(z), …,A0(z)是定义在复平面上的一组没有公共零点的全纯函数, 则方程

Φ(z,W)=Ak(z)Wk+Ak-1(z)Wk-1+…+

A1(z)W+A0(z)=0

(1)

设W(z)是由式(1)定义在复平面上的不可约k值代数体函数, 称z0是W(z)的临界点, 当且仅当Ak(z0)=0 或者Φ(z0,W)与偏导数ΦW(z0,W)有公共根, 所有临界点的集合称为临界集, 记为Sw;其补集Tw=-Sw称为正则集. 每一个临界点z0Sw是孤立点, 在z0附近 |(z-z0)kW(z)|有界,他们是可去奇点或极点, 在球面上按球距度量是连续的. 对于代数体函数的一些性质, 我们只需在正则集Tw中讨论, 剩下的孤立临界点则可由连续性确定[1-2].

孙道椿和高宗升[7]定义了代数体函数的运算,一个k值代数体函数W(z)与一个s值代数体函数M(z)的和是一个ks值代数体函数(W+M)(z)：

{(wj(z)+mt(z)),b):j=1,2,…,k;t=1,2,…,s}.

(2)

为W(z)关于a的亏量,

为W(z)关于a的Valiron亏量.

当分支数k=1时代数体函数即退化为亚纯函数情况.

Nevanlinna五值定理是亚纯函数的唯一性理论的经典结果, 叙述如下:

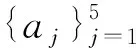
则f(z)≡g(z).

涉及重值的唯一性问题是亚纯函数唯一性理论的重要内容, 仪洪勋从重值的角度改进了定理A：

1≤tq≤tq-1≤…≤t2≤t1≤+∞.

(3)

若对任意j=1,2,…,q有

则f(z)≡g(z).

当式(5)不满足时, 情况会怎样呢? Ueda[8]在考虑亏量的条件下得到下列结果：

仪洪勋对定理C做了进一步改进，得到下面2个定理.

如果

则f(z)≡g(z).

如果

则f(z)≡g(z).

1 主要结果

本文将定理D、定理E推广到代数体函数：

1≤tq≤tq-1≤…≤t2≤t1≤+∞.

(6)

若对任意j=1,2,…,q有

再设

如果

则W(z)≡M(z).

(i)如果q=6k且

则W(z)≡M(z).

(ii)如果q=5k且

则W(z)≡M(z).

如果

则W(z)≡M(z).

(i)如果q=6k且

则W(z)≡M(z).

(ii)如果q=5k且

则W(z)≡M(z).

2 引理

引理1[9]W(z)、M(z)是2个非常数不可约的代数体函数,分别定义为

Φ(z,W)=Ak(z)Wk+Ak-1(z)Wk-1+…+A0(z)=

ψ(z,M)=Bs(z)Ms+Bs-1(z)Ms-1+…+B0(z)=

则下面叙述等价:

(1)W(z)≡M(z),

(2)存在W(z)、M(z)的正则元素(wi(z),a)=(mj(z),a),

(3)结式R(Φ,ψ)≡0.

引理2[2]设W(z)是不可约k值代数体函数,M(z)是不可约s值代数体函数,W(z)≢M(z), 值集W(0)、M(0)中均不含∞,则

T(r,W±M)≤T(r,W)+T(r,M)+log 2.

(14)

3 定理的证明

定理1的证明(i)先假定aj(j=1,2,…,q)是q个不同的有限值, 设W(z)≢M(z).由式(6)有

不妨假定值集W(0)、M(0)中均不含∞, 否则同乘以适当的因子zn. 由引理2有

(17)

即

由假设W(z)≢M(z)及引理1知,W(z)-M(z)没有恒等于0的分支,因此

n(r,W-M=0).

再由代数体函数第一基本定理及引理2可得

k(T(r,w)+T(r,M))+O(1),

(18)

k(T(r,w)+T(r,M))+O(1).

(19)

由式(20)及定理中条件(10)可得

T(r,W)

(21)

同理

及

T(r,M)

(23)

由式(20)、(23)可得

(24)

由式(21)、(22)可得

由定理中的条件(10)可知式(24)、(25)中至少有一个为矛盾不等式,于是W(z)≡M(z).

定理2的证明类似定理1,可假定aj(j=1,2,…,q)是q个不同的有限值,设W(z)≢M(z).由式(17)～(19)可得

式(26)、(27)相加有

S(r,W)+S(r,M).

(28)

由条件(13)得

再由式(28)即得B1=B2=0, 这与式(13)矛盾, 于是W(z)≡M(z).定理 2 证毕.

参考文献：

[1] 何育赞, 萧修治. 代数体函数与常微分方程[M]. 北京: 科学出版社, 1988.

[2] 孙道椿, 高宗升. 代数体函数的定理[J]. 数学学报, 2006, 49(5): 1027-1032.

Sun D C,Gao Z S. The theorem of algebroid functions[J]. Acta Mathematica Sinica, 2006, 49(5): 1027-1032.

[3] 高宗升, 王凤竹. 覆盖曲面定理与代数体函数的重值[J]. 数学学报, 2001, 44(5): 805-814.

Gao Z S,Wang F Z. Theorems of the covering surfaces and multiple values of the algebroid functions[J]. Acta Mathematica Sinica, 2001, 44(5): 805-814.

[4] Gao L Y. Value distribution of differential polynomials[J]. Journal of Mathematics, 2003, 23(1): 59-63.

[5] 杨乐. 值分布及其新研究[M]. 北京: 科学出版社, 1982.

[6] 仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社, 1995.

[7] 孙道椿, 高宗升. 代数体函数的唯一性定理[J]. 华南师范大学学报:自然科学版,2005(3): 80-85.

Sun D C,Gao Z S. Uniqueness theorem of algebroidal functions[J].Journal of South China Normal University:Natural Science Edition, 2005(3): 80-85.

[8] Ueda H. Unicity theorems for meromorphic or entire functions[J]. Kodai Mathematical Journal, 1980, 3(3): 457-471.

[9] 孙道椿. 代数体函数的增长性[J]. 华南师范大学学报:自然科学版, 2006(3): 1-6.

Sun D C. On the growth of algebroid functions[J]. Journal of South China Normal University:Natural Science Edition, 2006(3): 1-6.