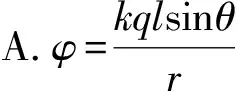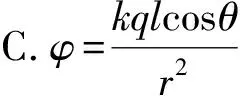用定性和半定量分析法求解一类新型高考选择题
2014-08-28
(江苏省姜堰中学,江苏 泰州 225500)
赵凯华老师在《定性和半定量物理学》中指出:“当一位成熟的物理学家进行探索的科学研究,常常从定性或半定量的方法入手…,他们通过定性和半定量的估算,力求对问题的性质、解的概貌取得一个总体的估计和理解.”所谓定性和半定量分析法就是粗略确定研究对象是否具有某种性质,确定某个物理量变化范围的一种研究方法,由于用定性和半定量的方法对问题的分析更能突出物理思想和方法,更有助于培养学生的物理直觉能力和推理能力,所以学会用定性和半定量分析法去分析研究问题对物理学习和研究具有重要意义.近年来高考中出现了一类考查方法的新颖的选择题,要求考生对某些问题的解是否合理进行正确的分析和判断.考生无法用常规物理方法求解,常常感觉“山穷水尽疑无路”.但如果学生掌握了定性和半定量的研究方法,很快就能找到解决这类选择题的突破口,从而“柳暗花明又一村”.下面举例说明定性和半定量分析的几种常用方法.
1 估算分析法
所谓估算分析法就是对某个物理量的可能范围、数量级进行粗略的计算.估算类问题文字简洁,已知条件少,待求量和已知量之间的联系比较隐蔽,学生常常束手无策.

图1
例1(2011江苏) 如图1所示,演员正在进行杂技表演.由图可估算出他将一只鸡蛋抛出的过程中对鸡蛋所做的功最接近于( ).
A.0.3J B.3J
C.30J D.300J
本题考查功能关系及对估算问题的处理.一只鸡蛋的质量大约为0.06kg,由图1结合人的身高与身体各部分的比例可知鸡蛋上升的最大高度约为0.5m,鸡蛋从速度为零开始到最高点的过程中,人对鸡蛋做的功转化为鸡蛋的动能,而动能又全部转化为最高点的重力势能,故有W=mgh=0.06×10×0.5J=0.3J,故A选项正确(估算题只要数量级正确即可).
本题是一道估算题,不过分追求数据的准确性,只要能保证数量级吻合就可以,还要能将问题转换为物理模型,并能运用物理方法进行处理.考生刚接触到此题,经常感到束手无策,但只要考生会用定性和半定量分析的方法,估算出鸡蛋的质量以及鸡蛋上升的大致高度,就能很快得出正确的答案.需要注意的是处理好本题还需要考生对一些生活中的物理量有清楚的认识(例如鸡蛋的质量),另外要有较好的观察能力(例如鸡蛋上升的最大高度).
2 理想分析法
所谓理想分析法就是运用理想模型在理想状态下进行计算和推理分析的一种研究方法.
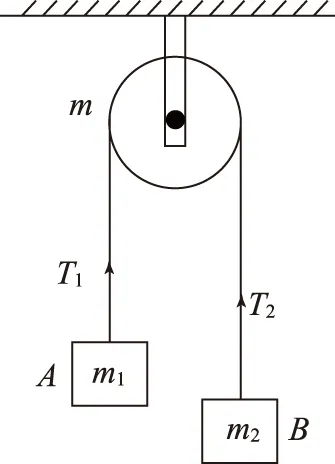
图2
例2(2011福建) 如图2所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦,设细绳对A和B的拉力大小分别为T1和T2,已知下列四个关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( ).
解法1(定量求解):
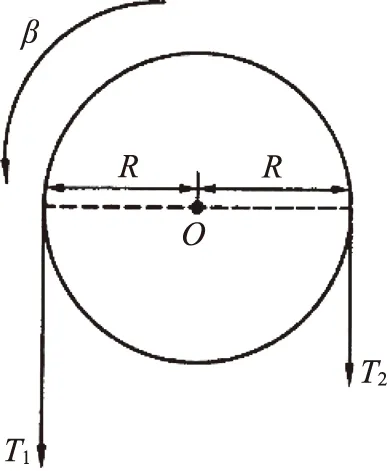
图3
如图3所示,设m1>m2,则A向下加速运动,B向上加速运动,设加速度大小为a.
由牛顿第二定律,m1g-T1=m1a,T2-m2g=m2a.
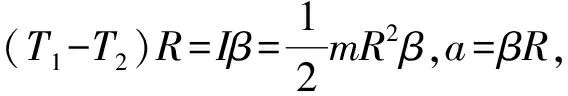
解法2(定性分析):
(1)假设m1=m2,两物体处于平衡状态,绳的拉力为T1=m1g=m2g,选项C正确.

(3)假设m1≫m2,令m=0,系统的加速度趋近重力加速度g,T1=T2=2m2g,或假设m1≪m2,令m=0,系统的加速度趋近重力加速度g,T1=2m1g,故选项C正确.
由于滑轮质量未知,本题绳中拉力需要用转动惯量和转动定律来定量求解,这种解法一般考生难以掌握.如果运用“极限法”分析在滑轮不受重力、或绳子两端物体重力相差很大的特殊受力情形下的解,并与预期结果相同,可方便求解.
3 量纲分析法
任何物理规律的表达式在给出了物理量数量关系的同时,也给出了物理量单位之间的关系,等式两边应该具有相同的量纲.这种运用物理量单位关系定性判断解的合理性的方法即“量纲分析法”.量纲分析法是20世纪初提出的,在物理领域建立数学模型的一种方法,它是在经验和实验的基础上,利用物理定律的量纲齐次原则,确定各物理量之间的关系.
例3(2012北京) “约瑟夫森结”由超导体和绝缘体制成.若在结两端加恒定电压U,则它会辐射频率为ν的电磁波,且ν与U成正比,即ν=KU.已知比例系数K仅与元电荷e的2倍和普朗克常量h有关.你可能不了解此现象的机理,但仍可运用物理学中常用的方法.在下列选项中,推理判断比例系数K的值可能为( ).

解法2:把本题四个选项比例系数K的表达式逐一代入题中公式ν=KU,比较等式两边的单位是否相等.如把选项B代入ν=KU中,化简整理得hν=2Ue,显然等式两边都是能量量纲,故B选项正确.用同样的方法可方便判断出A、C、D选项错误.
本题是一道有特色的选择题,灵活考查了考生分析物理问题的能力,难度系数为0.48左右.试题给出了一个高中不可能学到的公式,用常规方法无法求解,但从量纲的角度定性分析就能很容易得到正确的答案.
4 对称分析法
由于物质世界存在某些对称性,使得物理学理论也具有相应的对称性,从而使得对称现象普遍存在于各种物理现象和物理规律中,应用这种对称性不仅能帮助我们认识和探索物质世界的某些规律,也能帮助我们去求解某些具体问题,这种思维方法在物理学中称为对称分析法.
例4(2010安徽) 如图4所示,有一带电荷量为+q的点电荷与均匀带电圆形薄板相距为2d,此点电荷到带电薄板的垂线通过板的圆心.若图中a点处的电场强度为零,则图中b点处的电场强度大小是( ).
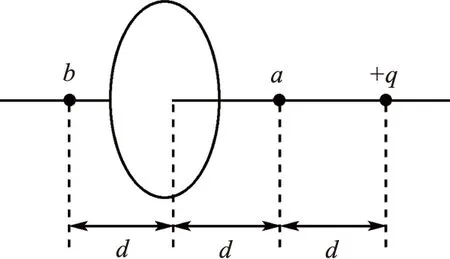
图4



在解决对称类问题时,我们不必总是从题目涉及的方向、位置入手,有时从其对称的一面(这一面经常是我们熟知的知识)考虑或统筹兼顾,往往能事半功倍.
5 等效替代法
所谓等效替代法就是在保证某些特定方面效果等同的前提下,用理想的、熟悉的、简单的事物替代实际的、陌生的、复杂的事物进行研究的方法.等效替代法是物理学研究中应用普遍、表述简洁的方法.
例5(2010福建) 如图5所示,为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧,与O点相距为r(r 图5 本题中带电圆环不能看成点电荷,中学生很难通过定量方法求解场强,当两带电圆环在相距很远的特殊位置时,可等效为电量集中于圆心的点电荷,运用点电荷场强公式,可以得到解答. 极限分析法是一种科学的思维方法,它在物理解题中有着广泛的应用,学会用极限分析法分析物理问题,可以帮助学生理解物理规律及其在具体问题中所包含的物理意义,掌握物理规律的适用条件,避免死套公式,并且还能使习惯性思维得到突破性训练,培养创造性思维能力. 例6(2010上海) 设相距为l,电荷量分别为+q和-q的点电荷构成电偶极子.如图6所示,取二者连线方向为y轴方向,中点O为原点,建立如图6所示的xOy坐标系,P点距坐标原点O的距离为r(r≫l),P、O两点间连线与y轴正方向的夹角为θ,设无穷远处的电势为零,P点的电势为φ,静电力常量为k.下面给出φ的四个表达式只有一个是合理的,请你分析判断合理表达式应为( ). 图6 当r→∞,φ=0(无穷远处电势为零),可排除B答案. 当θ=90°时,P点位于等量异种电荷的中垂线上,电势为零,排除A、D答案,正确答案为C. 在中学阶段对电势的表达式不做要求,因此此题无法进行定量运算.但只要转换思维,取r→∞以及θ=90°两种极限情况,很快就能得到答案. 这类选择题选题新颖、独特,有较高的区分度,对中学物理教学有较好的导向作用.长期以来,中学物理教学中过分强调定量计算,加之学生在理解、分析物理问题时的直觉往往是错误的,导致大多数同学总以为只有定量计算的方法是可靠的,而定性和半定量的方法是靠不住的.因此在平时教学中要增强学生对定性和半定量的分析方法的认识,培养学生掌握一些常用方法,并适当进行一些训练,不仅可以提高学生解决定性分析和半定量分析计算类题目的能力,更重要的是可以促进学生对物理问题和物理规律的理解,有利于学生形成良好的思维习惯.
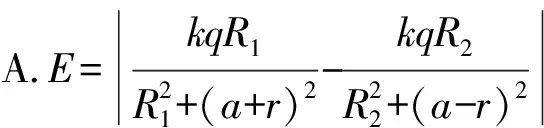
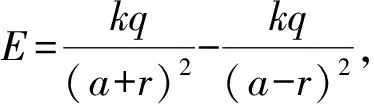
6 极限分析法