物理图像法的妙用

2014-08-28

物理之友 2014年4期

(北京市第三十五中学，北京 100032)

图像法作为物理学中的一种重要科学方法，一直以来都是高考的热点.其原因在于图像可以直观、综合、形象地传递大量信息.对理解物理意义、提升学生的物理素养都有重要价值.

1 利用物理图像法直观解题

在北京市某年高中毕业会考物理试题中，充分体现了图像法解题的直观性.题目如下：水平放置的弹簧振子做简谐运动的周期为T.t1时刻振子不在平衡位置且速度不为零；t2时刻振子的速度与t1时刻的速度大小相等，方向相同；t3时刻振子的速度与t1时刻的速度大小相等，方向相反.若t2-t1=t3-t2，则( ).

A.t1时刻、t2时刻与t3时刻，弹性势能都相等

B.t1时刻与t3时刻，弹簧的长度相等

C.t3-t1=(2n+1/2)T(n=0、1、2……)

D.t3-t1=(n+1/2)T(n=0、1、2……)

解析：此题的参考答案是A、C.答案A无疑是正确的，但对于答案C，笔者却有不同看法，现分析如下：对于t1，由于每个周期中都有两个振动时刻符合v1=v2，其中一个与t1同相，一个与t1不同相，根据v3=-v1和t2-t1=t3-t2两个条件来判断，t1与两时刻必为不同相的振动，所以振子位移S2=-S1，t2-t1≠nT.同样，因为v3=-v1，所以S3=±S1但若S3=S1，加上条件t2-t1=t3-t2，则t2必为振子在最大位移处，故S3=-S1.接下来用物理图像法来分析t3-t1的可能情况：

如图1所示，由简谐运动的图像可知如果满足条件S1=-S2=-S3和t2-t1=t3-t2，则t1必等于nT/2+T/8或nT/2+3T/8(n=0、1、2……).

图1

当t1=n1T/2+T/8时，t2=n1T/2+n2T+7T/8，t2-t1=n2T+3T/4，则t3-t1=2(t2-t1)=(2n+1)T+T/2(如图像中的t1、t3)；当t1=n1T/2+3T/8时，t2=n1T/2+n2T+5T/8，t2-t1=n2T+T/4，则t3-t1=2(t2-t1)=2nT+T/2(如图像中的t1′、t3′).

由于题目中四个选项前有“则”字，有肯定的意思，所以不妥，如果说“可能是”会更恰当一些.显然，本题用图像法更为简洁明了.并且由于图像可直观地表现振子的位移、速度，因此本题表明了处理关于简谐运动问题最简单直观的方法就是图像法，这一认识具有迁移价值.

2 利用物理图像法分析实验误差

在“测电源电动势和内电阻”实验中，学生对电表内阻引起的系统误差往往不易理解.笔者在多次执教高三物理的过程中，曾分别用了多种不同的方法去解释本实验中的系统误差，比如用戴文宁定理(准确但专业性太强，对于普通学生很难理解和接受)、伏安法测电阻的系统误差(易于理解和记忆，但比较牵强)、测量数据点相对于真实数据点的平移(容易理解，但很麻烦且不便于记忆).以下笔者就用图像法加以阐释.

图2

本实验的过程不再赘述，实验最后都是用电源的U-I图像去求解电源电动势和内电阻.根据闭合电路欧姆定律，有：E=U+Ir，若以I为自变量，U为应变量，转化为标准的一次函数形式，则有：U=-rI+E.式中“-r”为斜率k，“E”为截距b.通过图像上的斜率和截距即可求得E和r(如图2)，这个结论是学生们已于理解并熟悉的.以下就对电流表的两种不同接法引起的系统误差做出分析.

图3

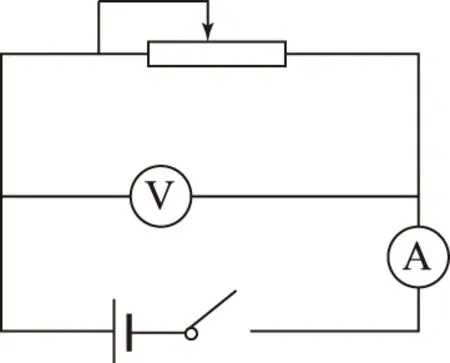
图4

同样地，如果我们用另一种电路来测量E和r(如图4)，则引起系统误差的是电流表的分压作用，电压表的测量值小于路端电压U，应用闭合电路欧姆定律有，E=U测+I测(r+RA)，化简为标准的一次函数形式则变为：U测=-(r+RA)I测+E.

由此可以看出，由测量数据描绘出的图线中，斜率k的绝对值为RA与r的串联电阻，而截距则为E，所以E测=E,r测=RA+r>r.由于RA与r比较接近，因此这种方法所测得的r测相对误差会很大.但如果事先已得知电流表的内阻，则用此方法得出的r测只需要做一下修正，即可求得电源内电阻的阻值，即r=r测-RA.

根据此实验可以得出，对于我们没见过的比较生疏的一次函数图像，我们可以用这样的步骤去分析误差和求解物理量：①找参量，将图像中的横、纵坐标轴表示的物理量与要求解的物理量用常见的一个公式表示出来，或者找出它们之间的关系式；②化简为标准的一次函数形式；③分析式中的斜率和截距，看它们代表什么.用这种方法，我们可以将许多一次函数的图像问题迅速地解决，充分体现了该方法的效力.

3 利用立体图像法解决物理难题

对物理学中的图像法，函数图像、模拟图像、直观图形等形式已有了诸多体现，一道初中物理光学“错题”提醒我们注意立体图像法的作用.

太阳光沿与水平面

成30°角的方向射来，为了使反射光线成水平方向，则平面镜跟水平面所成的角度为( ).

A．15° B．30°

C．75° D．120°

图5

笔者认为，该题题干表述不明确，容易引起误导.如果反射光线与入射光线在同一个竖直面内(如图5)，则很容易证明法线与水平面的夹角α为15°或75°，则平面镜跟水平面所成的角度应为90°-α，结果为75°或15°.但是，如果反射光线虽然沿水平方向，却不与入射光线在同一竖直平面内，则就有一定的取值范围，而不是一个定值(如图6)，AO为入射光线，OB为反射光线，OB在水平面1内，AO与OB决定的平面为平面2，OC为法线.分别过A、C作平面1的垂线，垂足分别为D、E，分别过D、E作平面1、2的相交线OB的垂线，垂足分别为F、G.由已知条件可知，∠AOD=30°，则入射光线AO与反射光线OB的夹角θ的变化范围应为30°≤θ≤150°.

当θ=30°时，法线与水平面的夹角α=∠COE=15°，则平面镜跟水平面所成的角度90°-α=75°；当θ=150°时，法线与水平面的夹角α=∠COE=75°，则平面镜跟水平面所成的角度90°-α=15°；当θ从30°到150°连续变化时，平面镜跟水平面所成的角度从75°连续变化到15°，是一个连续的减函数，因此是一系列连续的不确定的值.所以，严格来说，此题应选A、B、C.